POJ 1159 Palindrome

POJ 1159 Palindrome

题意:

给出一个字符串，求最少插入多少个字符可以让该字符串变成回文字符串

思路1:

思路1是卡过去的 (用 \(short\) 换 \(int\) 和用了一个常数优化)，所以建议如果只看一种思路的话，移步思路2。

目的是使得整个字符串变成回文字符串，所以定义 \(f[i][j]\) 为将字符串 \(i-j\) 变成回文串需要插入的最少字符串。

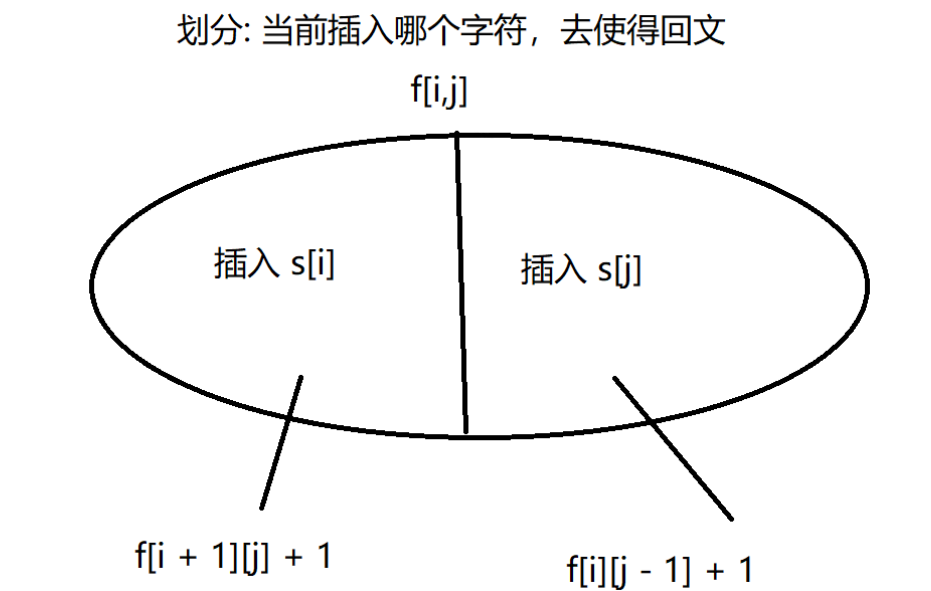
注意这里有一个常数优化剪枝，就是当 \(s[i] == s[j]\) 时，可以直接返回 \(f[i + 1][j - 1]\) ，因为 从 \(f[i][j]\) 到 \(f[i +1][j-1]\) 一共就只有两种方法

• \(f[i][j]->f[i+1][j] + 1->f[i + 1][j - 1] + 1 ->f[i + 1][j - 1]\)
• \(f[i][j] ->f[i + 1][j - 1]\)

显然第二种肯定优于第一种，所以可以直接剪枝。

思路2:

倒着再把数组存一遍，找到两个字符串的 最长公共子序列 (LCS)，字符串的长度减去 LCS 的长度就是结果。

最长公共子序列的转移方程为:

\(f[i][j] = max(f[i - 1][j],f[i][j - 1])\)

如果 \(a[i] == a[j]\) ，\(f[i][j] = max(f[i][j],f[i - 1][j - 1] + 1)\)

所以可以发现，这里直接使用滚动数组，就可以解决掉上面改用 \(short\) 来避免 \(MLE\) 的问题。

问题:

• 没有注意空间大小，MLE 了, \(5000 * 5000 * 4 (int\; 4byte) / 1024 = 97,656.25KB\) 显然，超过的题目的限制 655536KB，然后观察了一下数据量，发现用 short 类型就可以了 \(5000 * 5000 * 2 (short\; 2byte) / 1024 = 48,828.125KB\)

实现:

//思路1
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 5e3 + 5, INF = 5003;
char s[N];
short f[N][N];

short dp(int i, int j)
{
    if (i >= j)
        return 0;
    if (f[i][j] != INF)
        return f[i][j];

    //f[i][j]->f[i+1][j] + 1->f[i + 1][j - 1] + 1 ->f[i + 1][j - 1]
    //f[i][j] ->f[i + 1][j - 1];
    //上面肯定不如下面优，所以直接剪枝
    if (s[i] == s[j])
    {
        return f[i][j] = min(f[i][j], short(dp(i + 1, j - 1)));
    }

    f[i][j] = min(short(dp(i + 1, j) + 1), short(dp(i, j - 1) + 1));

    return f[i][j];
}

int main()
{
    int n;
    scanf("%d", &n);
    scanf("%s", s + 1);
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= n; j++)
            f[i][j] = INF;

    printf("%d\n", dp(1, n));
    return 0;
}

//思路2
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 5e3 + 5;
char a[N], b[N];
int f[2][N];
int main()
{
    int n;
    scanf("%d", &n);
    scanf("%s", a + 1);
    for (int i = 1; i <= n; i++)
        b[n - i + 1] = a[i];

    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= n; j++)
        {
            f[i & 1][j] = max(f[(i & 1) ^ 1][j], f[i & 1][j - 1]);
            if (a[i] == b[j])
                f[i & 1][j] = max(f[i & 1][j], f[(i & 1) ^ 1][j - 1] + 1);
        }
    }
    printf("%d\n", n - f[n & 1][n]);
    return 0;
}