6-1 Is Topological Order (30 分)

Write a program to test if a give sequence Seq is a topological order of a given graph Graph.

Format of functions:

bool IsTopSeq( LGraph Graph, Vertex Seq[] );

 

where LGraph is defined as the following:

typedef struct AdjVNode *PtrToAdjVNode; 
struct AdjVNode{
    Vertex AdjV;
    PtrToAdjVNode Next;
};

typedef struct Vnode{
    PtrToAdjVNode FirstEdge;
} AdjList[MaxVertexNum];

typedef struct GNode *PtrToGNode;
struct GNode{  
    int Nv;
    int Ne;
    AdjList G;
};
typedef PtrToGNode LGraph;

 

The function IsTopSeq must return true if Seq does correspond to a topological order; otherwise return false.

Note: Although the vertices are numbered from 1 to MaxVertexNum, they are indexed from 0 in the LGraph structure.

Sample program of judge:

#include <stdio.h>
#include <stdlib.h>

typedef enum {false, true} bool;
#define MaxVertexNum 10  /* maximum number of vertices */
typedef int Vertex;      /* vertices are numbered from 1 to MaxVertexNum */

typedef struct AdjVNode *PtrToAdjVNode; 
struct AdjVNode{
    Vertex AdjV;
    PtrToAdjVNode Next;
};

typedef struct Vnode{
    PtrToAdjVNode FirstEdge;
} AdjList[MaxVertexNum];

typedef struct GNode *PtrToGNode;
struct GNode{  
    int Nv;
    int Ne;
    AdjList G;
};
typedef PtrToGNode LGraph;

LGraph ReadG(); /* details omitted */

bool IsTopSeq( LGraph Graph, Vertex Seq[] );

int main()
{
    int i, j, N;
    Vertex Seq[MaxVertexNum];
    LGraph G = ReadG();
    scanf("%d", &N);
    for (i=0; i<N; i++) {
        for (j=0; j<G->Nv; j++)
            scanf("%d", &Seq[j]);
        if ( IsTopSeq(G, Seq)==true ) printf("yes\n");
        else printf("no\n");
    }

    return 0;
}

/* Your function will be put here */

 

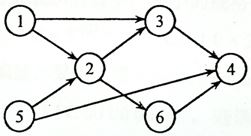
Sample Input (for the graph shown in the figure):

6 8
1 2
1 3
5 2
5 4
2 3
2 6
3 4
6 4
5
1 5 2 3 6 4
5 1 2 6 3 4
5 1 2 3 6 4
5 2 1 6 3 4
1 2 3 4 5 6

 

结尾无空行

Sample Output:

yes
yes
yes
no
no

 

结尾无空行

 

int p[10000];
bool IsTopSeq(LGraph Graph, Vertex Seq[])
{
    for (int i = 0; i < Graph->Nv; i++)
    {
        p[Seq[i] - 1] = i;
    }
    for (int i = 0; i < Graph->Nv; i++)
    {
        PtrToAdjVNode cur = Graph->G[i].FirstEdge;
        while (cur)
        {
            if (p[i] > p[cur->AdjV])
            {
                return false;
            }
            cur = cur->Next;
        }
    }
    return true;
}

拓扑序列的构成：

每次选取入度为0的节点，所以一个图可以有不同的拓扑序列

判定拓扑序列只需判断给出的序列中节点的位置是否与图中的位置不符，

比如5 2 1 6 3 4这个序列，由于2排在了1的前面，所以不能构成拓扑序列

第一个for循环，将给出的序列按位置赋值，p[5]=0，p[2]=1.... p[4]=5

然后第二个for循环，通过访问邻接表的数据，如果p[i]>p[cur->Adjv],则说明存在一个结点，位置大于前面，此时不符合拓扑序列，则return false

如果走完全部序列都没有发现问题，那么此序列为拓扑序列

然后此题目还有一个坑“Note: Although the vertices are numbered from 1 to MaxVertexNum, they are indexed from 0 in the LGraph structure.”

所以p[Seq[i] - 1] = i，赋值的时候需要减1