BUAA_OO第一单元多项式求导博客总结

BUAA_OO第一单元多项式求导博客总结

一、基于代码度量分析结构

下面对最后一次作业进行分析。

（一）复杂性分析

Complexity metrics    
Method CogC ev(G) iv(G) v(G)
Constant.derivation() 0 1 1 1
Constant.getCoeff() 0 1 1 1
Constant.setCoeff(BigInteger) 0 1 1 1
Constant.toString() 0 1 1 1
MainClass.main(String[]) 5 1 4 4
Poly.add(Exp,String) 2 1 3 3
Poly.addPoly(Poly,String) 1 1 2 2
Poly.addPolyItem(PolyItem,String) 6 3 4 5
Poly.derivation() 1 1 2 2
Poly.getPolyItemArrayList() 0 1 1 1
Poly.multiFactor(Factor) 1 1 2 2
Poly.multiPolyItem(PolyItem) 1 1 2 2
Poly.multiply(Exp) 2 1 2 2
Poly.setPolyItemArrayList(ArrayList<PolyItem>) 0 1 1 1
Poly.toString() 6 1 4 5
PolyFactory.setPolyClass(String) 90 19 24 33
PolyItem.derivation() 4 3 4 4
PolyItem.equals(Object) 9 7 3 8
PolyItem.getCoeff() 0 1 1 1
PolyItem.getFactorArrayList() 0 1 1 1
PolyItem.getItemType() 0 1 1 1
PolyItem.multiFactor(Factor) 27 8 13 13
PolyItem.multiPolyItem(PolyItem) 1 1 2 2
PolyItem.multiply(Exp) 2 1 2 2
PolyItem.setCoeff(BigInteger) 0 1 1 1
PolyItem.setFactorArrayList(ArrayList<Factor>) 0 1 1 1
PolyItem.setItemType(TreeMap<String, BigInteger>) 0 1 1 1
PolyItem.toString() 17 1 10 10
Power.derivation() 3 1 3 3
Power.getIndex() 0 1 1 1
Power.setIndex(BigInteger) 0 1 1 1
Power.toString() 3 1 2 3
Triangle.Triangle(BigInteger,String,Poly) 0 1 1 1
Triangle.derivation() 7 1 5 5
Triangle.getContain() 0 1 1 1
Triangle.getIndex() 0 1 1 1
Triangle.getType() 0 1 1 1
Triangle.setIndex(BigInteger) 0 1 1 1
Triangle.setType(String) 0 1 1 1
Triangle.toString() 3 1 3 3
WrongFormat.printStackTrace() 0 1 1 1

由表格可看出，PolyFactory.setPolyClass(String)，PolyItem.toString()和PolyItem.multiFactor(Factor)复杂度高，原因是前两者运用了递归调用，而后者与其他类的数据耦合度高。

（二）代码量分析

Lines of code metrics     
Method CLOC JLOC LOC NCLOC RLOC
Constant.derivation() 0 0 8 8 36.36%
Constant.getCoeff() 0 0 3 3 13.64%
Constant.setCoeff(BigInteger) 0 0 3 3 13.64%
Constant.toString() 0 0 5 5 22.73%
Exp.derivation() 0 n/a n/a 1 33.33%
Factor.derivation() 0 n/a n/a 2 50.00%
MainClass.main(String[]) 0 0 17 17 89.47%
Poly.add(Exp,String) 0 0 10 10 10.99%
Poly.addPoly(Poly,String) 0 0 5 5 5.49%
Poly.addPolyItem(PolyItem,String) 0 0 20 20 21.98%
Poly.derivation() 0 0 8 8 8.79%
Poly.getPolyItemArrayList() 0 0 3 3 3.30%
Poly.multiFactor(Factor) 0 0 5 5 5.49%
Poly.multiPolyItem(PolyItem) 0 0 5 5 5.49%
Poly.multiply(Exp) 0 0 10 10 10.99%
Poly.setPolyItemArrayList(ArrayList<PolyItem>) 0 0 3 3 3.30%
Poly.toString() 0 0 19 19 20.88%
PolyFactory.setPolyClass(String) 8 0 141 136 92.76%
PolyItem.derivation() 2 0 35 34 19.44%
PolyItem.equals(Object) 0 0 18 18 10.00%
PolyItem.getCoeff() 0 0 3 3 1.67%
PolyItem.getFactorArrayList() 0 0 3 3 1.67%
PolyItem.getItemType() 0 0 3 3 1.67%
PolyItem.multiFactor(Factor) 0 0 57 57 31.67%
PolyItem.multiPolyItem(PolyItem) 0 0 5 5 2.78%
PolyItem.multiply(Exp) 0 0 10 10 5.56%
PolyItem.setCoeff(BigInteger) 0 0 3 3 1.67%
PolyItem.setFactorArrayList(ArrayList<Factor>) 0 0 3 3 1.67%
PolyItem.setItemType(TreeMap<String, BigInteger>) 0 0 3 3 1.67%
PolyItem.toString() 2 0 32 31 17.78%
Power.derivation() 0 0 19 19 45.24%
Power.getIndex() 0 0 3 3 7.14%
Power.setIndex(BigInteger) 0 0 3 3 7.14%
Power.toString() 0 0 14 14 33.33%
Triangle.Triangle(BigInteger,String,Poly) 0 0 5 5 7.04%
Triangle.derivation() 3 0 34 32 47.89%
Triangle.getContain() 0 0 1 1 1.41%
Triangle.getIndex() 0 0 3 3 4.23%
Triangle.getType() 0 0 3 3 4.23%
Triangle.setIndex(BigInteger) 0 0 3 3 4.23%
Triangle.setType(String) 0 0 3 3 4.23%
Triangle.toString() 0 0 14 14 19.72%
WrongFormat.printStackTrace() 0 0 4 4 66.67%

由表格看出，PolyFactory.setPolyClass(String)和PolyItem.multiFactor(Factor)代码行数多，这与代码架构有关，前者为处理字符串只使用了一个方法，后者为项与因子的乘法。

ClassCLOCJLOCLOC
Constant 0 0 22
Factor 0 0 4
MainClass 0 0 19
Poly 1 0 91
PolyFactory 10 0 152
PolyItem 6 0 180
Power 0 0 42
Triangle 3 0 71
WrongFormat 0 0 6

类代码量如图所示，PolyFactory和PolyItem代码量较大，原因同前面。

（三）代码架构

1.类和继承关系

Factor抽象类：常数，幂，三角，Poly的父类，抽象方法:Poly derivation()

Exp 接口：由Factor抽象类和项继承，抽象方法:Poly derivation()

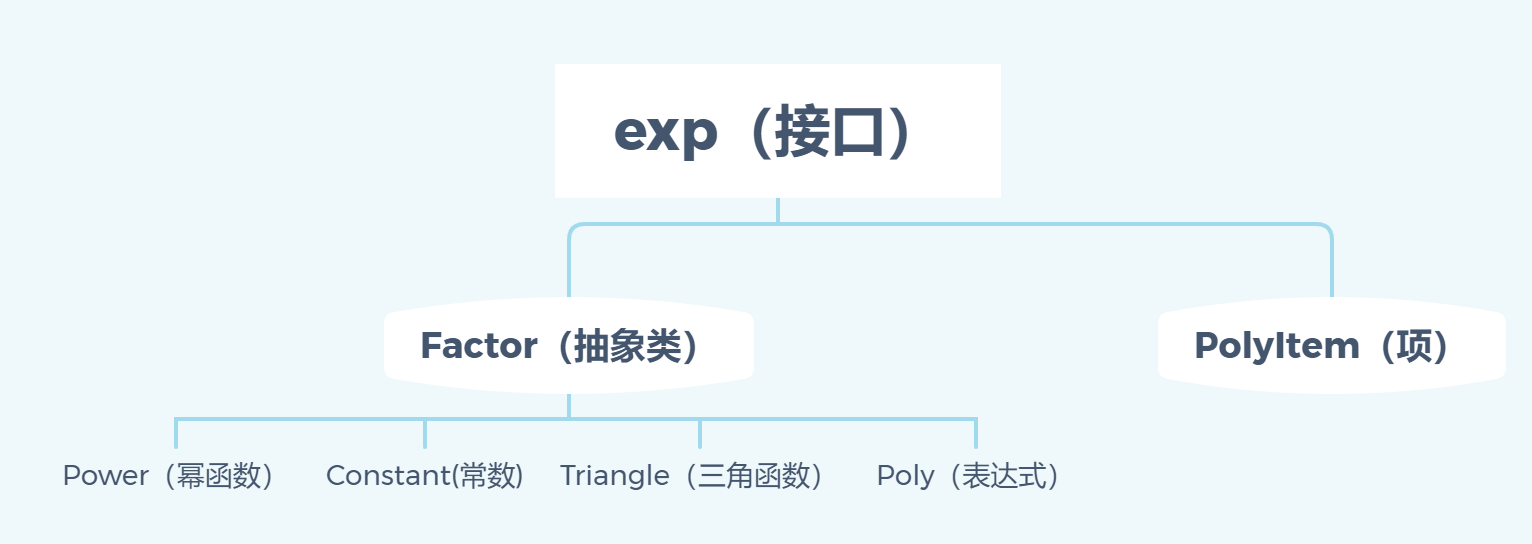
2.类和方法简介

下图为自己画的主要部分的uml类图：

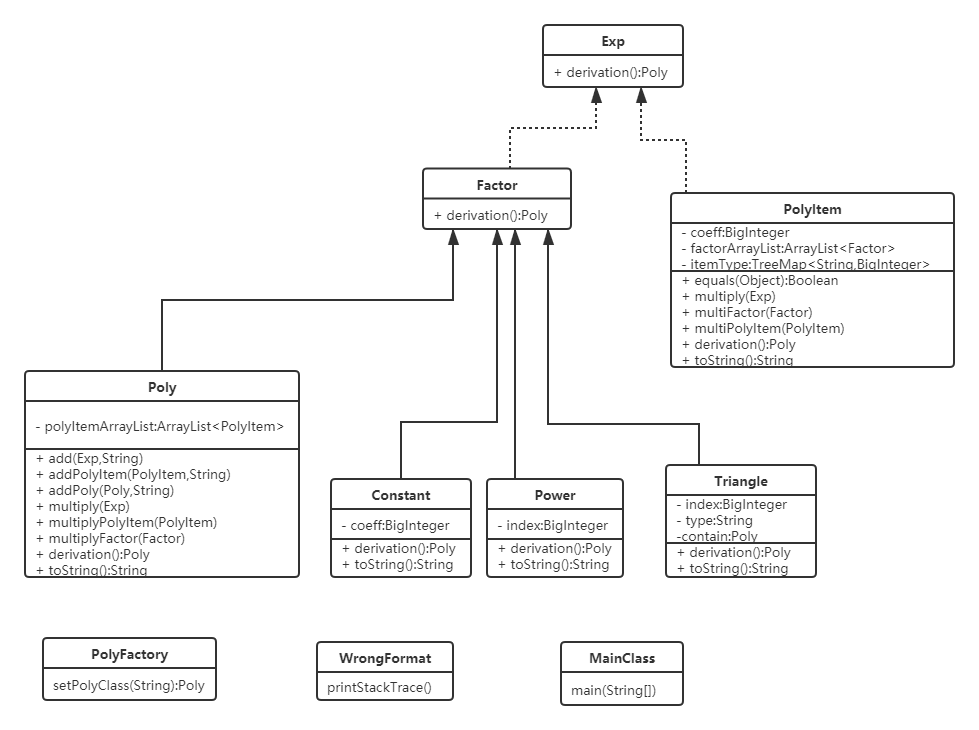
四种因子和项都有derivation()和toString()方法（toSring进行了覆写），分别实现了得到求导和结果输出，PolyItem的equals方法实现了判断两个项是否为同类项，此外还实现了PolyItem的乘法和Poly类的加乘运算方法。

3.字符串处理

字符串处理使用的是PolyFactory工厂模式的Poly setPolyClass(String string)方法，传入从标准输入获取的字符串，返回此字符串对应的Poly 实例。

在处理字符串之前先将所有的** 替换为 ^,方便后续匹配处理。

由于表达式可抽象成Factor([+*]Factor)*，只要在第一个Factor前加上一个加号即可抽象成一般形式([+*]Factor)+，然后利用matcher.find方法进行循环匹配即可完成表达式的建立。patternFactor正则表达式如下，为三个因子的并（幂函数|常数|三角函数）：

private static Pattern patternFactor = Pattern.compile(
        "((\\s*x\\s*(\\^\\s*([+-]?\\d+))?\\s*)|(\\s*([+-]?\\d+)\\s*)|" +
        "(\\s*((sin|cos)\\s*\\(\\s*(.+)\\s*\\))\\s*(\\s*\\^\\s*([+-]?\\d+))\\s*))");

在这里使用变量end来记录当前所匹配到的最后一个字符的下一个字符位置，matcher.find(int index)方法是从index开始查找第一个匹配的字符串，主体代码如下：

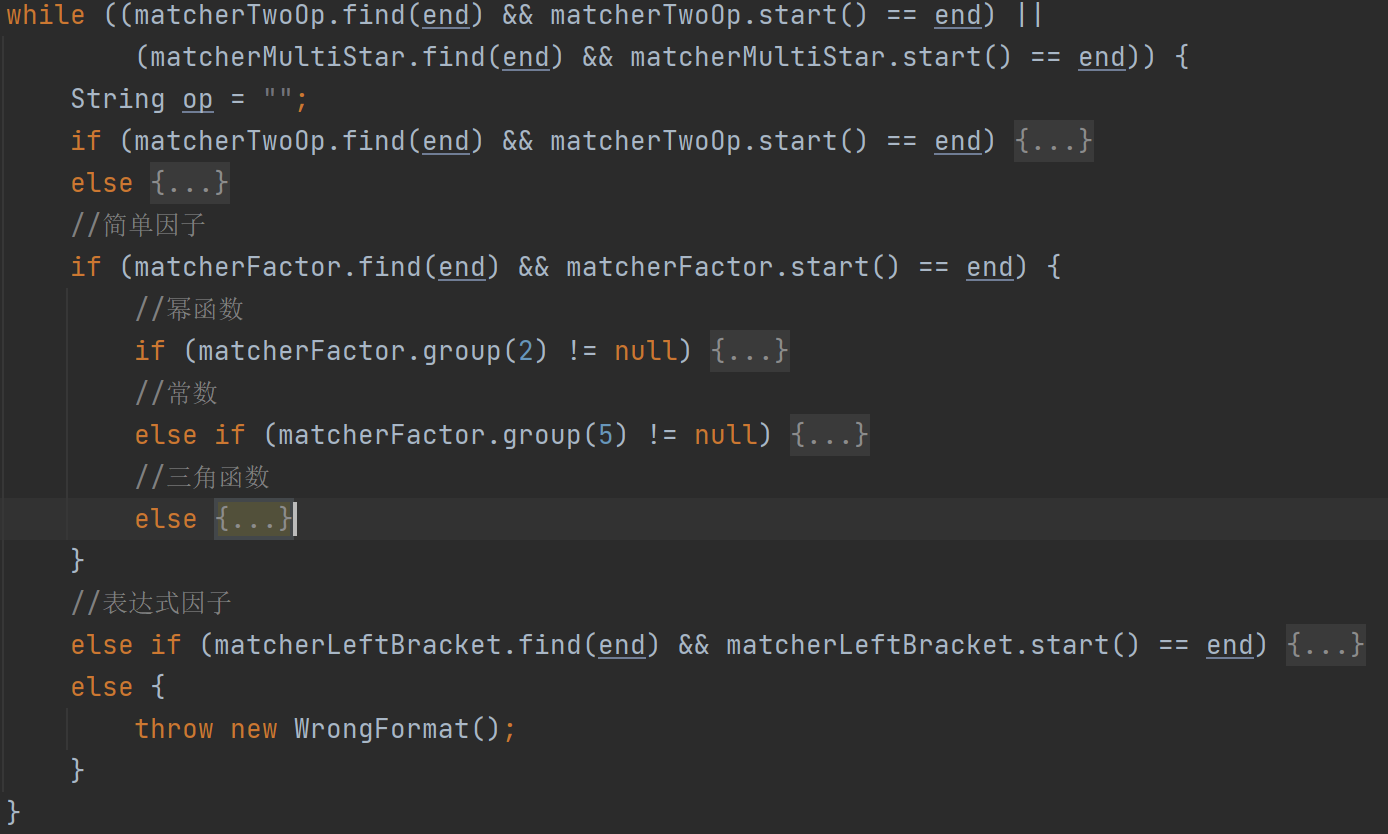
在匹配运算符的过程中，若匹配到的是加减运算符，则将现有的polyItem实例放入poly中(使用poly.add(polyItem,addOp))，并新建一个polyItem类，并使用addOp保存加减运算符；若匹配到乘号，则不更新polyItem。

在匹配完运算符后匹配因子，通过判断是哪一类因子，新建一个相应的实例，并放入polyItem中。

表达式因子的匹配方法是建立一个存左括号index的栈，从开始匹配的左括号的index开始，碰到左括号就入栈，碰到右括号就出栈，进行循环匹配，栈空则break，获取此时的左右括号index，再通过str.subString(left,right)来获取表达式因子对应的字符串，利用PolyFactory递归解析。

对于三角函数，由于正则表达式的贪婪匹配，匹配到的不一定是正确的三角函数（由于括号内部可以为表达式因子），所以在匹配到三角函数后，sin|cos后面的内部结构用表达式因子的匹配方法来处理。

4.求导过程

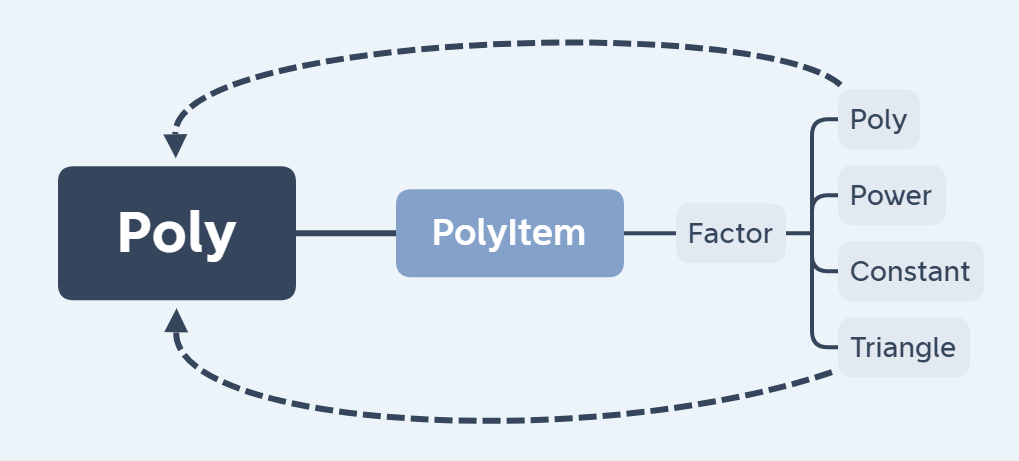
图中所有类都继承了Exp接口，即都有Poly derivation()求导方法，从输入字符串中解析出Poly类后，一步步向下层调用求导方法，最终得到其导数（Poly类）。每个求导方法都构造了新的Poly类实例来存放导数，在求导过程中不会改变原poly的内部值，保证了正确性。

下面简要介绍各类求导方法：

  1. Poly：PolyItem的导数之和。

  2. PolyItem：运用求导公式(ab)' = a'b + b'a，其中，a为factorArrayList的第一项，为factor类，b为factorArrayList的剩余项构成的remain（新构造的PolyItem），a'和b'为Poly类，上述求导公式即变成了a.dervation().multiply(b) + b.dervation().multiply(a)，再使用Poly类的add和multiply方法递归后可以得到最终的结果。

  3. Factor: Power和Constant显然，Poly类在前面已经提到，Triangle利用求导公式y'(t(x)) = y'(t)*t'(x)进行链式求导并将各部分相乘得到最后的导数。

5.toString输出

与求导过程类似，将下层toString方法的返回值传递给上层，最终得到Poly所对应的字符串。

6.WRONG FORMAT 判断

  1. 表达式格式错误：在匹配运算符时，若无法连续匹配会自动退出循环，故只要判断匹配的最后一个字符（运用matcher.end方法）是否和从输入读取的字符串长度相等即可；在匹配Factor时，如果匹配不到任何一个输出WRONG FORMAT!。

  2. 限制输入表达式中出现的指数（包括幂函数和三角函数）绝对值不超过50（十进制），超过此范围需要输出WRONG FORMAT!。

  3. 三角函数括号内为因子，不能为表达式或项，如果不是因子则输出WRONG FORMAT!。

  4. 处理字符串时，在将所有的** 替换为 ^之前现在顶层main函数内判断字符串是否含有非法字符^，有则输出WRONG FORMAT!。

7.一点点优化

  1. 相同的PolyItem项合并。

  2. 一些输出优化，比如系数为1或-1、指数为1等情况。

  3. 系数为0的项不输出。

（四）优点和缺点

1.优点

正确性尚可，运用了面向对象所学知识，除PolyFactory类外各类基本达到高内聚低耦合要求。

2.不足之处

PolyFactory类写的很长，但由于使用了大量matcher .find, .group, .start, .end参数过多，数据耦合度太高，尝试分成多个方法失败(风格分扣20警告)。

没有运用数据结构中建树的方法存表达式，数据存储方式较差。

有的类没有写构造方法，直接使用了set方法进行赋值，增加了未初始化的隐患。

使用了较多get set方法，对用户不透明。

优化做的比较粗糙，有的地方由于架构的问题导致优化较为困难，而且第二次作业还因为优化跪了，性能很一般。

三、踩过的坑、遇过的bug

由于懒惰，本单元没有学习写评测机，也没有进行大量测试，导致在强测互测中发现bug。所以，一定要进行大量测试包括覆盖性测试和边界测试！学会构造评测机！

在编程过程中遇到了深浅拷贝问题，后来通过每次求导建立新的Poly实例和不打开括号求导解决了这个问题。

由于有的函数没有构造方法直接使用get和set方法赋值，出现了"非静态方法引用静态参数"的错误，并且无法通过将方法改成静态解决，上网找寻解决方法最后通过设置构造方法解决，建立类后要建立构造方法，不仅能避免未初始化还能避免无法预测的问题。

第二次强测和互测中发现一个bug，原因是在PolyItem中第175行添加了如下代码以优化程序输出长度：

else if (poly.getPolyItemArrayList().size() == 1) {
    str = str + "*" + poly.getPolyItemArrayList().get(0).toString();
}

在项中出现只包含0的表达式因子即会出错，如(+0)*sin(x)，原因是在表达式递归中+0项的tostring方法的返回值为空字符串，去掉此段程序即可改正，要注意在程序中不要出现使用空容器的情况。

第三次作业中测bug: cos((x + 1 + x**2)) ** 3输出wrongformat，这是由于在PolyFactory中替换字符串后递归导致再次判断错误，递归函数要注意递归后的正确性，和栈溢出的风险。

互测bug1：PolyFactory类sin（表达式）没有对表达式使用.trim函数去两端空白符导致WRONG FORMAT!判断错误，个例问题，和架构有关，可以忽略。

bug2：在polyItem equals 方法中，由于第二次作业统一为sin（x），cos（x），itemtype的key写的是sin和cos，但此次括号内值不同，导致此种判断在item中出现的sin和cos次数相同时出错，key存的字符串修改为sin|cos（内含物）形式，扩展新功能时要查看以前的构造是否正确。

总结：从上述总结中看出，错误集中在PolyFactory类中的setPolyClass方法和PolyItem类,正是前文代码度量分析中代码行和圈复杂度较大的类和方法，这给了我构造类和方法时复杂度不要太高的经验教训。

三、找别人bug时的策略

由于本人没有构造评测机，而且精力和能力有限，互测时随缘盲测bug，没有结合被测程序的代码设计结构来设计测试用例。在构造样例时采取的策略是将题中所有元素和注意事项以及自己写程序时对特殊情况的处理构造的测试样例，这样做"中奖率很低"，三次作业只hack了两次（也是因为没有积极构造和提交测试数据，而且有两次作业都是进的大佬屋），以后一定学会搭建评测机。

四、重构经历总结

本次只进行了一次重构，在第二次作业的时候进行了重构，下面通过类图展示三次作业迭代过程。

第一次作业

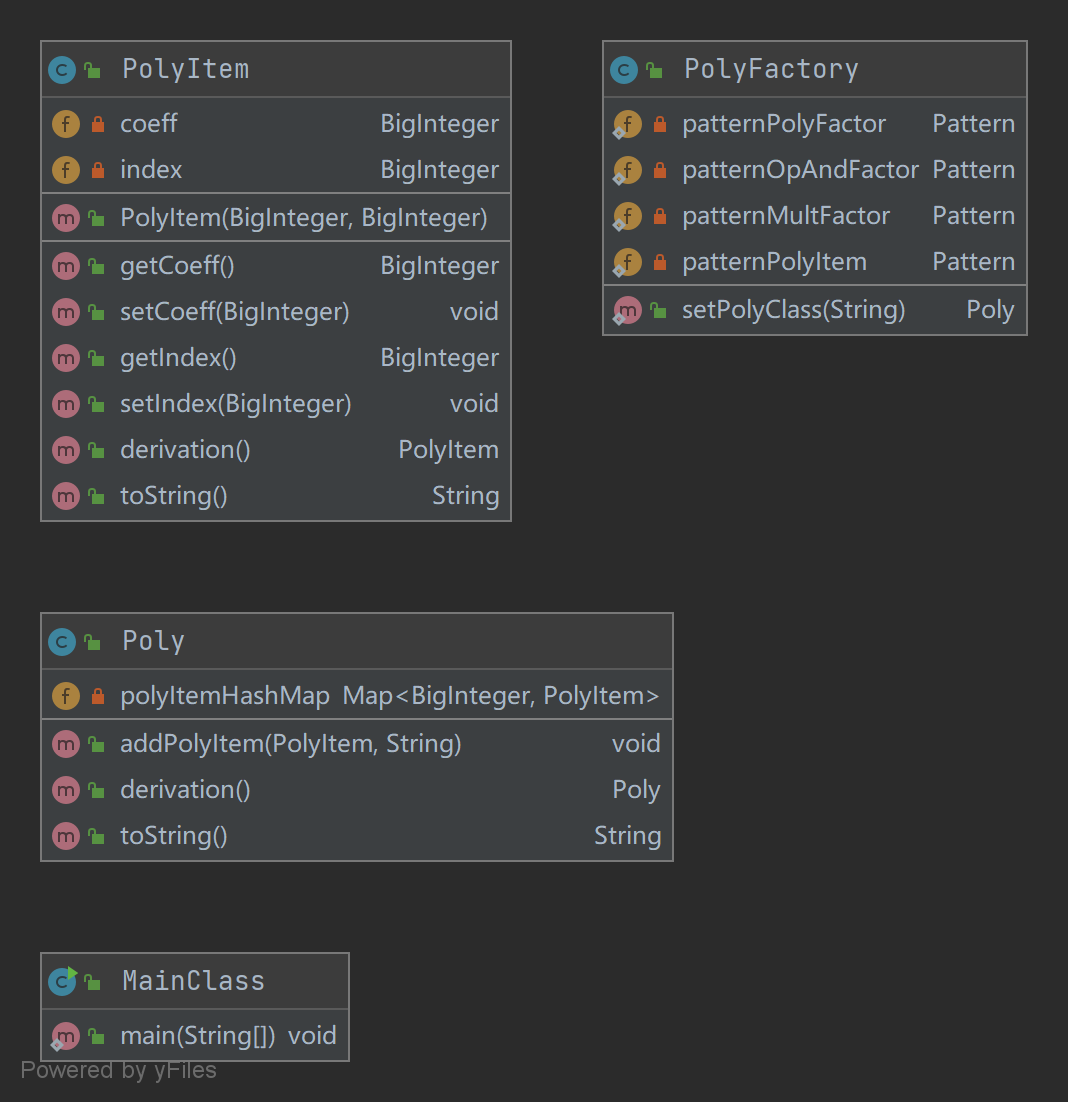
以下是第一次作业uml类图，第一次作业只是简单建立了PolyItem(项)和Poly(表达式)类，PolyItem的field包含coeff（系数）和index（指数），Poly使用TreeMap作为容器存储PolyItem，key为指数。

第二次作业

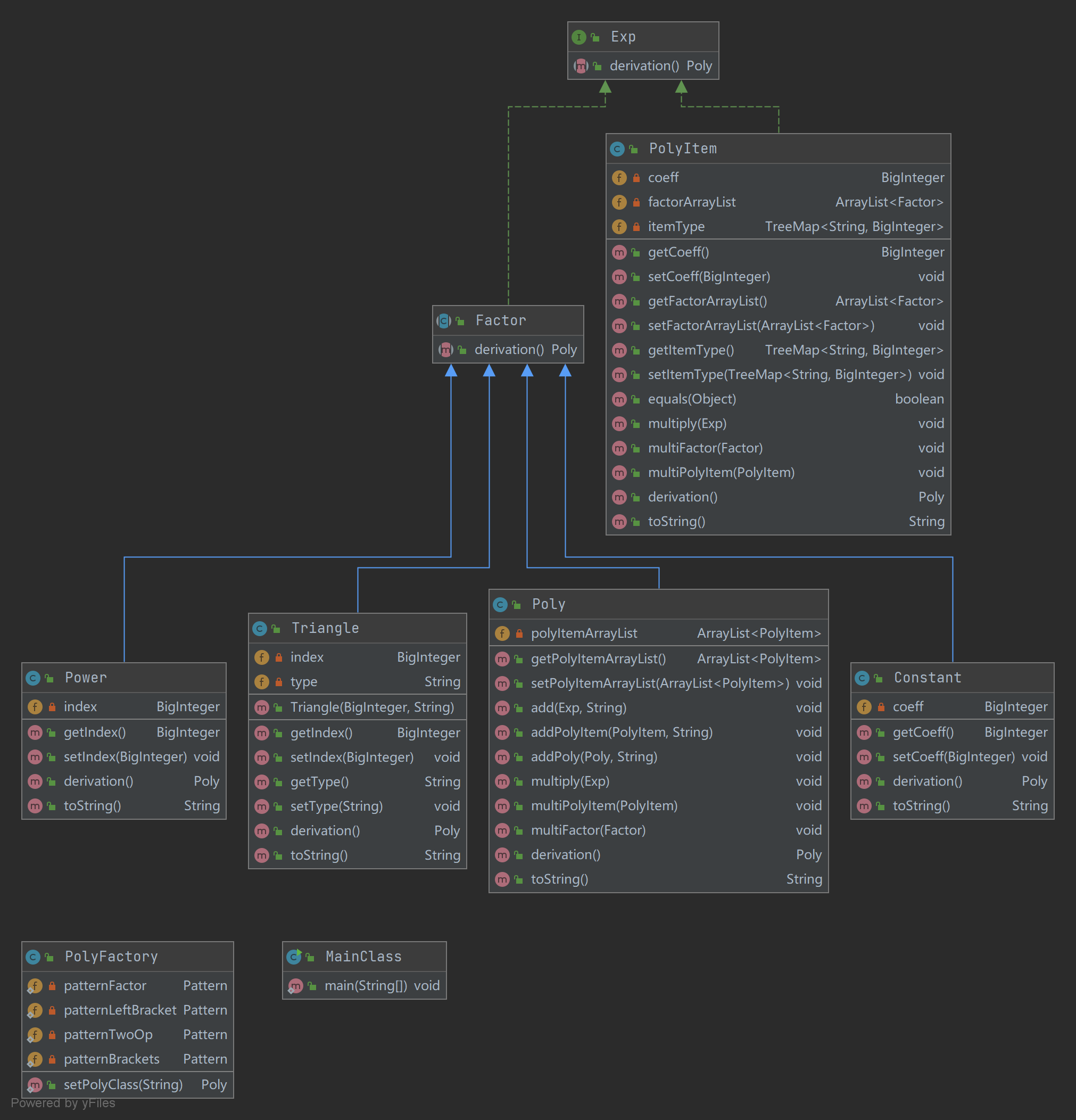
下图为第二次uml类图，本次作业着重构建了不同的容器类型和类的继承关系，实现了第一单元的大多数功能。

第三次作业

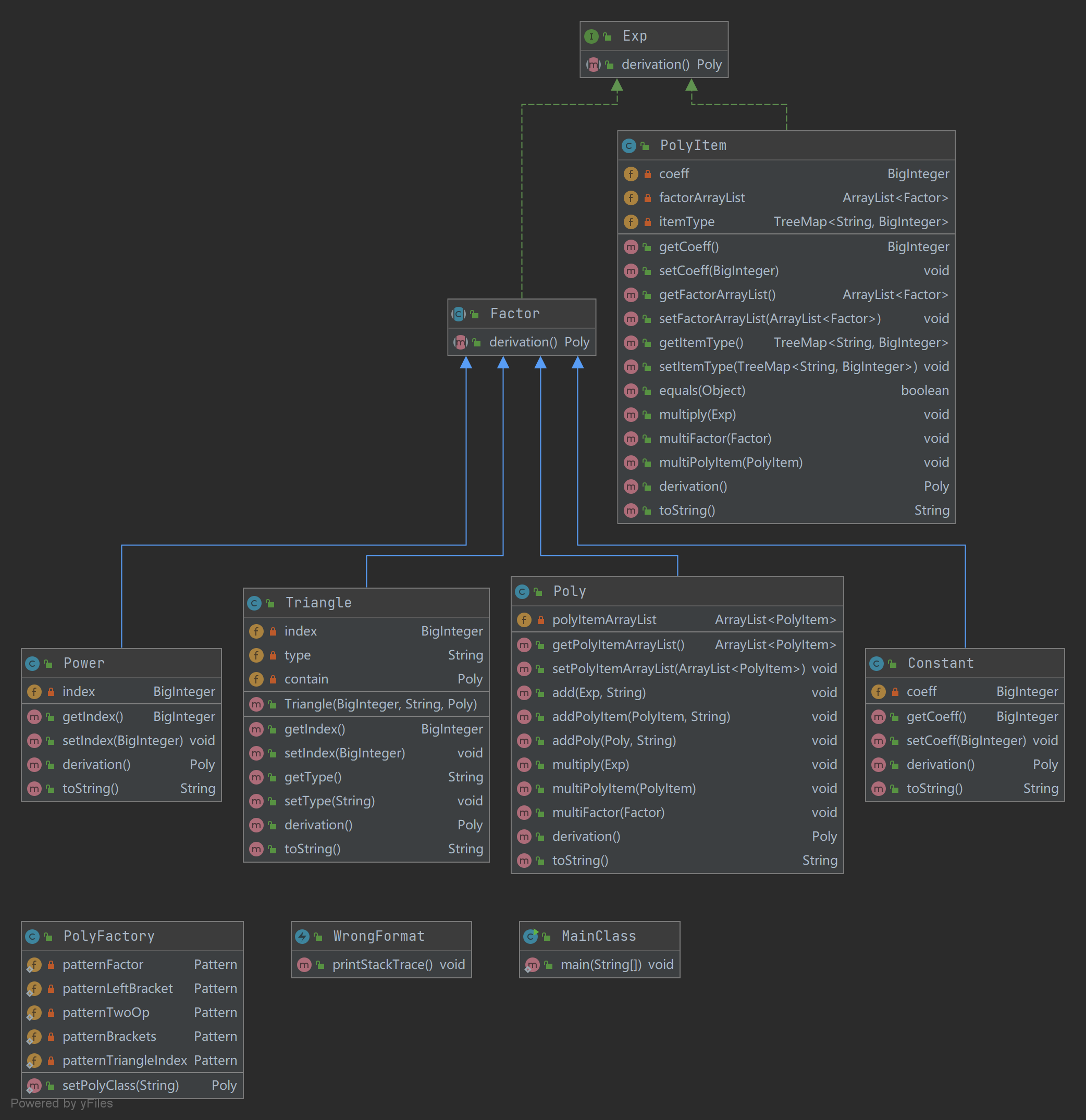
下图为第三次作业UML类图,可以看出仅新添了WrongFormat类，Triangle新增contain field。

五、心得体会

一定要进行大量测试包括覆盖性测试和边界测试！学会构造评测机！

好的构造是成功的一半，能减轻后序迭代的工作量，也能一定程度上减少bug

pre作业对本次作业有很大帮助。

OO确实挺肝的，de没给输入的测试点也挺头秃，但能学到东西，写完觉得自己编程能力upup，大概面向对象思想也有些提升

posted @ 2021-03-28 20:41  zxj9  阅读(145)  评论(0)    收藏  举报