LCT

$LCT$，全称 $Link$ $Cut$ $Tree$，可以解决动态树问题。

首先要知道一条虚边连接了 $2$ 个 $splay$，而这些 $splay$ 构成了 $LCT$。

动态树（LCT）

$isroot$ 操作

如果一个点不是根，则考虑它既不是父亲的左儿子也不是父亲的右儿子。代码：

bool isroot(int x){
    return tr[tr[x].p].s[0]!=x&&tr[tr[x].p].s[1]!=x;
}

$rotate$ 操作

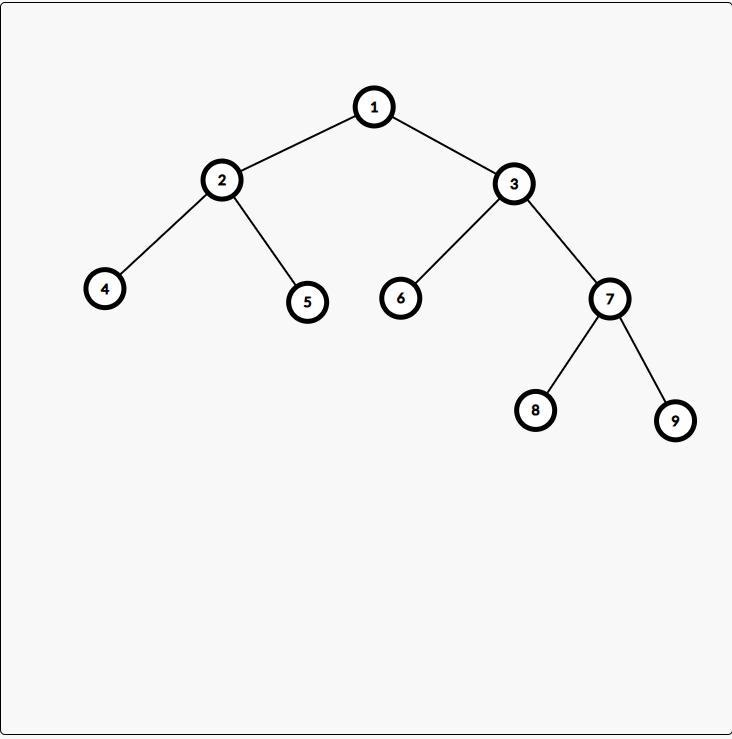
假设 $x$ 为 $7$，$y$ 为 $3$，$z$ 为 $1$，也就是说要把 $7$ 旋上去。考虑旋上去的话，就把父亲转到自己下面。于是先断开与父亲的边，连上与爷爷的边。

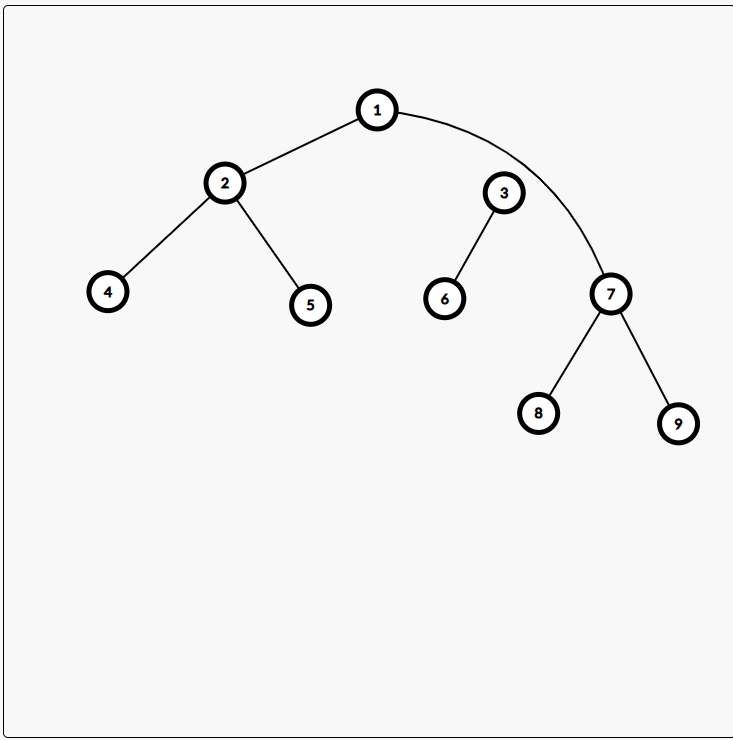
接下来发现父亲少了一个儿子，于是把自己的另外一边的儿子给父亲，同时把他连接自己的边断掉。

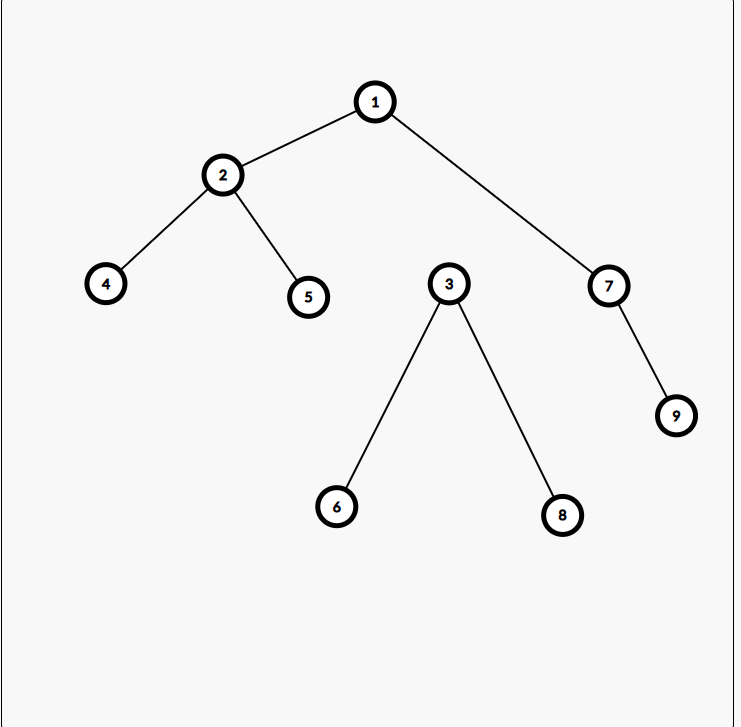
最后我们只需要链接 $x$ 和 $y$，只不过这次 $x$ 是父亲。

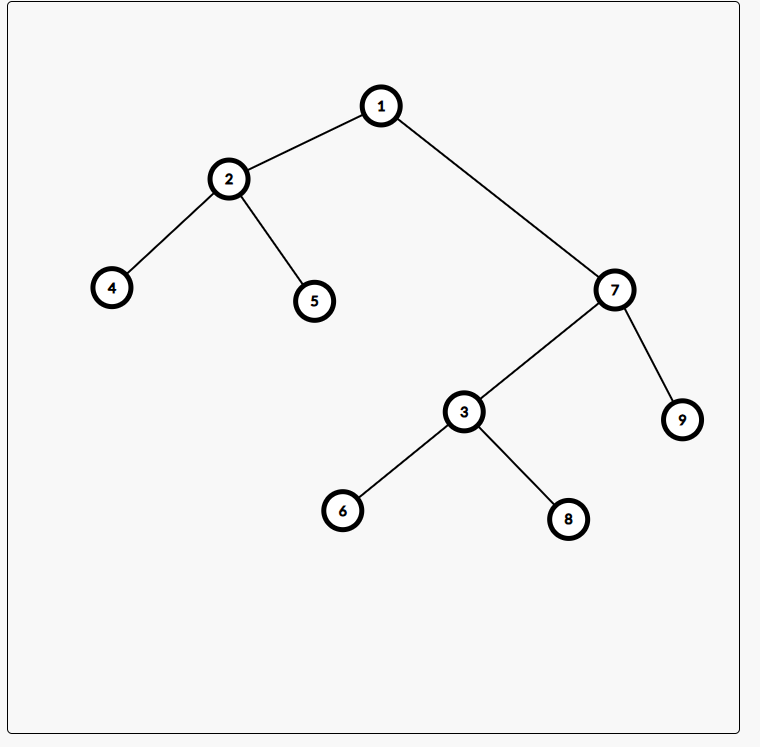
代码：

void rotate(int x){
    int y=tr[x].p,z=tr[y].p;
    int k=tr[y].s[1]==x;
    if(!isroot(y))tr[z].s[tr[z].s[1]==y]=x;
    tr[x].p=z;
    tr[y].s[k]=tr[x].s[k^1];
    tr[tr[x].s[k^1]].p=y;
    tr[x].s[k^1]=y;
    tr[y].p=x;
    pushup(y);
    pushup(x);
}

$splay$ 操作

先分类讨论一下，看 $x,y,z$ 在不在一条直线上，可以看一下图：

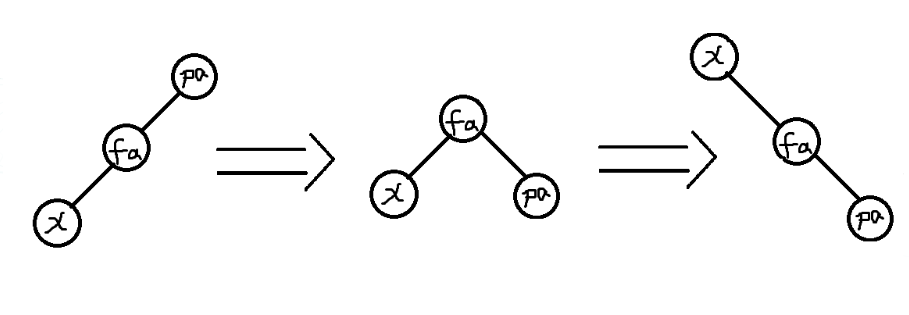
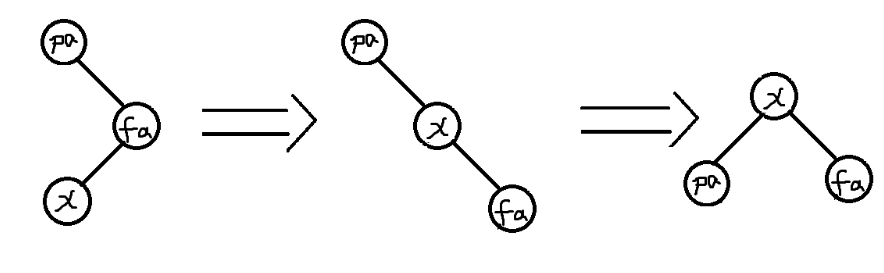
不难发现，如果在一条直线上，则先转 $y$，再转 $x$；否则连着转两下 $x$。这样一直操作直到 $x$ 被转到跟上。

但是在进行旋转之前，我们要先把转上去的路径做个 $pushdown$。代码：

void splay(int x){
    int top=0,r=x;
    stk[++top]=r;
    while(!isroot(r))stk[++top]=r=tr[r].p;
    while(top)pushdown(stk[top--]);
    while(!isroot(x)){
        int y=tr[x].p,z=tr[y].p;
        if(!isroot(y)){
            if((tr[y].s[1]==x)^(tr[z].s[1]==y))rotate(x);
            else rotate(y);
        }
        rotate(x);
    }
}

$access$ 操作

我们需要把根节点到 $x$ 的路径上的所有边变成实边。于是考虑先把 $x$ 在 $splay$ 上旋到根，然后更新右儿子（右儿子的原因是上面的 $rotate$ 是左旋，只有在右边才能转上去），再把 $x$ 变成其父亲，直到 $x$ 是根。代码：

void access(int x){
    int z=x;
    for(int y=0;x;y=x,x=tr[x].p){
        splay(x);
        tr[x].s[1]=y;
        pushup(x);
    }
}

$makeroot,findroot$ 操作

把 $x$ 换成整棵树的根。于是我们需要先把 $x$ 到根的路径上全部变成实边，然后把 $x$ 转到根上，最后传一下标记即可。代码：

void makeroot(int x){
    access(x);
    splay(x);
    pushrev(x);
}

找一个点的根其实就是，先把 $x$ 到根的路径上全部变成实边，然后把 $x$ 转到根上（这个和上面一样）。然后一直往左儿子走（因为 $access$ 动的是右儿子，这里转到根后往祖先走就是往左儿子走），走到的最后一个点就是根。代码：

int findroot(int x){
    access(x);
    splay(x);
    while(tr[x].s[0]){
        pushdown(x);
        x=tr[x].s[0];
    }
    splay(x);
    return x;
}

$split$ 函数

下面认为两件套指的是先打通 $x$ 到根的路径（换成实边），然后把 $x$ 转上去。

我们要拉出一条 $x\sim y$ 的路径作为一棵新的 $splay$，其实就是先把 $x$ 换成根，然后对 $y$ 做一个两件套。代码：

void split(int x,int y){
    makeroot(x);
    access(y);
    splay(y);
}

$link,cut$ 函数

首先连完边要保证是一棵树。于是先把 $x$ 换成根，然后看 $y$ 所在 $splay$ 的根是不是 $x$，如果不是，则把 $y$ 的父亲改为 $x$。代码：

void link(int x,int y){
    makeroot(x);
    if(findroot(y)!=x)tr[x].p=y;
}

断边直接把 $x,y$ 先单独拉出来，然后看 $y$ 的左儿子是不是 $x$ 和 $x$ 有没有右儿子。如果满足，则清空 $x$ 的父亲和 $y$ 的左儿子。代码：

void cut(int x,int y){
	split(x,y);
	if(tr[y].s[0]==x&&!tr[x].s[1])tr[x].p=tr[y].s[0]=0;
}

完整代码：

#include<bits/stdc++.h>
#define int long long
#define N 100005
using namespace std;
int n,m,stk[N];
struct node{
    int s[2],p,v,sum,rev;
}tr[N];
void pushrev(int x){
    swap(tr[x].s[0],tr[x].s[1]);
    tr[x].rev^=1;
}
void pushup(int x){
    tr[x].sum=tr[tr[x].s[0]].sum^tr[tr[x].s[1]].sum^tr[x].v;
}
void pushdown(int x){
    if(tr[x].rev){
        pushrev(tr[x].s[0]);
        pushrev(tr[x].s[1]);
        tr[x].rev=0;
    }
}
bool isroot(int x){
    return tr[tr[x].p].s[0]!=x&&tr[tr[x].p].s[1]!=x;
}
void rotate(int x){
    int y=tr[x].p,z=tr[y].p;
    int k=tr[y].s[1]==x;
    if(!isroot(y))tr[z].s[tr[z].s[1]==y]=x;
    tr[x].p=z;
    tr[y].s[k]=tr[x].s[k^1];
    tr[tr[x].s[k^1]].p=y;
    tr[x].s[k^1]=y;
    tr[y].p=x;
    pushup(y);
    pushup(x);
}
void splay(int x){
    int top=0,r=x;
    stk[++top]=r;
    while(!isroot(r))stk[++top]=r=tr[r].p;
    while(top)pushdown(stk[top--]);
    while(!isroot(x)){
        int y=tr[x].p,z=tr[y].p;
        if(!isroot(y)){
            if((tr[y].s[1]==x)^(tr[z].s[1]==y))rotate(x);
            else rotate(y);
        }
        rotate(x);
    }
}
void access(int x){
    int z=x;
    for(int y=0;x;y=x,x=tr[x].p){
        splay(x);
        tr[x].s[1]=y;
        pushup(x);
    }
}
void makeroot(int x){
    access(x);
    splay(x);
    pushrev(x);
}
int findroot(int x){
    access(x);
    splay(x);
    while(tr[x].s[0]){
        pushdown(x);
        x=tr[x].s[0];
    }
    splay(x);
    return x;
}
void split(int x,int y){
    makeroot(x);
    access(y);
    splay(y);
}
void link(int x,int y){
    makeroot(x);
    if(findroot(y)!=x)tr[x].p=y;
}
void cut(int x,int y){
	split(x,y);
	if(tr[y].s[0]==x&&!tr[x].s[1])tr[x].p=tr[y].s[0]=0;
}
signed main(){
    cin>>n>>m;
    for(int i=1;i<=n;i++){
        cin>>tr[i].v;
    }
    while(m--){
        int t,x,y;
        cin>>t>>x>>y;
        if(!t){
            split(x,y);
            cout<<tr[y].sum<<'\n';
        }
        else if(t==1)link(x,y);
        else if(t==2)cut(x,y);
        else{
            splay(x);
            tr[x].v=y;
            pushup(x);
        }
    }
    return 0;
}