AC自动机提高篇

文本生成器

首先考虑一个容斥，算出不包含任何一个单词的文章的数量。

我们设 \(dp_{i,j}\) 表示当前文章长度为 \(i\)，最后一个字符在 \(AC\) 自动机上的 \(j\) 号点的方案数。我们要求的答案就是 \(\displaystyle 26^m-\sum_{i=0}^{idx}f_{m,i}\)。

于是我们考虑怎么转移。

首先，我们在建立 \(AC\) 自动机的时候，如果发现一个节点 \(i\) 指向的 \(ne_i\) 节点有结束标记，那么我们把这个点也打上结束标记。其他东西没有区别

然后我们对于 \(AC\) 自动机上的每一个点 \(j\)，设他的其中一个字节点为 \(k\)。那么如果 \(k\) 节点没有结束标记，则 \(f_{i,k}+f_{i-1,j}\leftarrow f_{i,k}\)。于是就做完了，代码：

#include<bits/stdc++.h>
#define int long long
#define N 10005
#define M 105
#define mod 10007
using namespace std;
int tr[N][26],cnt[N],ne[N],n,m,idx,f[M][N];
char s[N];
//f_{i,j}表示字符串长度i，最后一个字符的点为j，且不包含任意一个模式串的方案数
int ksm(int x,int y){
	int res=1;
	while(y){
		if(y&1)(res*=x)%=mod;
		(x*=x)%=mod;
		y>>=1;
	}
	return res;
}
void ins(){
	int p=0;
	for(int i=0;s[i];i++){
		int t=s[i]-'A';
		if(tr[p][t]==0)tr[p][t]=++idx;
		p=tr[p][t];
	}
	cnt[p]=1;
}
void build(){
	queue<int>q;
	for(int i=0;i<26;i++){
		if(tr[0][i]!=0){
			q.push(tr[0][i]);
		}
	}
	while(!q.empty()){
		int t=q.front();
		q.pop();
		for(int i=0;i<26;i++){
			int c=tr[t][i];
			if(c==0){
				tr[t][i]=tr[ne[t]][i];
			}
			else{
				if(cnt[tr[ne[t]][i]]==1)cnt[tr[t][i]]=1;
				ne[c]=tr[ne[t]][i];
				q.push(c);
			}
		}
	}
}
signed main(){
	cin>>n>>m;
	for(int i=1;i<=n;i++){
		cin>>s;
		ins();
	}
	build();
	f[0][0]=1;//空字符串，方案数1
	for(int i=1;i<=m;i++){
		for(int j=0;j<=idx;j++){
			for(int k=0;k<26;k++){
				if(cnt[tr[j][k]]==1)continue;
				(f[i][tr[j][k]]+=f[i-1][j])%=mod;
			}
		}
	}
	int sum=ksm(26,m),res=0;
	for(int i=0;i<=idx;i++){
		(res+=f[m][i])%=mod;
	}
	if(sum<res)sum+=mod;
	cout<<sum-res;
	return 0;
}

数数

发现就是上一题的 \(dp\) 变成了数位 \(dp\)，于是我们采用记忆化搜索实现。

我们设 \(f_{i,j,k,l}\) 表示当前到了第 \(i\) 位数，最后一个数字在 \(AC\) 自动机上的位置为 \(j\)，并且当前前 \(i\) 位是或不是和限制的数完全相同，当前前 \(i\) 位是不是全是 \(0\)。

但是由于我们记搜是最后到只剩一位才返回答案，相当于是倒着算的，所以我们初始要把限制数字翻转。

剩下的 \(dp\) 方式几乎和上一题一样，代码：

#include<bits/stdc++.h>
#define int long long
#define N 1605
#define mod 1000000007
using namespace std;
int tr[N][10],cnt[N],ne[N],n,m,idx,f[N][N][2][2];
string t;
char s[N];
void ins(string s){
	int p=0;
	for(int i=0;s[i];i++){
		int t=s[i]-'0';
		if(tr[p][t]==0)tr[p][t]=++idx;
		p=tr[p][t];
	}
	cnt[p]=1;
}
void build(){
	queue<int>q;
	for(int i=0;i<10;i++){
		if(tr[0][i]!=0){
			q.push(tr[0][i]);
		}
	}
	while(!q.empty()){
		int t=q.front();
		q.pop();
		for(int i=0;i<10;i++){
			int c=tr[t][i];
			if(c==0){
				tr[t][i]=tr[ne[t]][i];
			}
			else{
				ne[c]=tr[ne[t]][i];
				cnt[c]|=cnt[ne[c]];
				q.push(c);
			}
		}
	}
}
int dp(int dep,int ac_pos,bool is_lim,bool has_zer){
	if(dep==0)return cnt[ac_pos]==0;
	if(cnt[ac_pos]==1)return 0;
	int &v=f[dep][ac_pos][is_lim][has_zer];
	if(v!=-1)return v;
	int lim=is_lim?(s[dep]-'0'):9ll;
	int sum=0;
	for(int i=0;i<=lim;i++){
		int p1=(has_zer&&(i==0))?0:tr[ac_pos][i];
		bool f1=(is_lim&&(i+'0'==s[dep]));
		bool f2=(has_zer&&(i==0));
		(sum+=dp(dep-1,p1,f1,f2))%=mod;
	}
	return v=sum;
}
signed main(){
	cin>>s+1>>n;
	int len=strlen(s+1);
	reverse(s+1,s+len+1);
	memset(f,-1,sizeof f);
	for(int i=1;i<=n;i++){
		cin>>t;
		ins(t);
	}
	build();
	int res=dp(len,0,1,1)+mod-1;
	if(res>mod)res-=mod;
	cout<<res;
	return 0;
}

阿狸的打字机

首先我们要建出失配树。什么是失配树？就是把每个点连向他的失配指针构成的一棵树。例如：

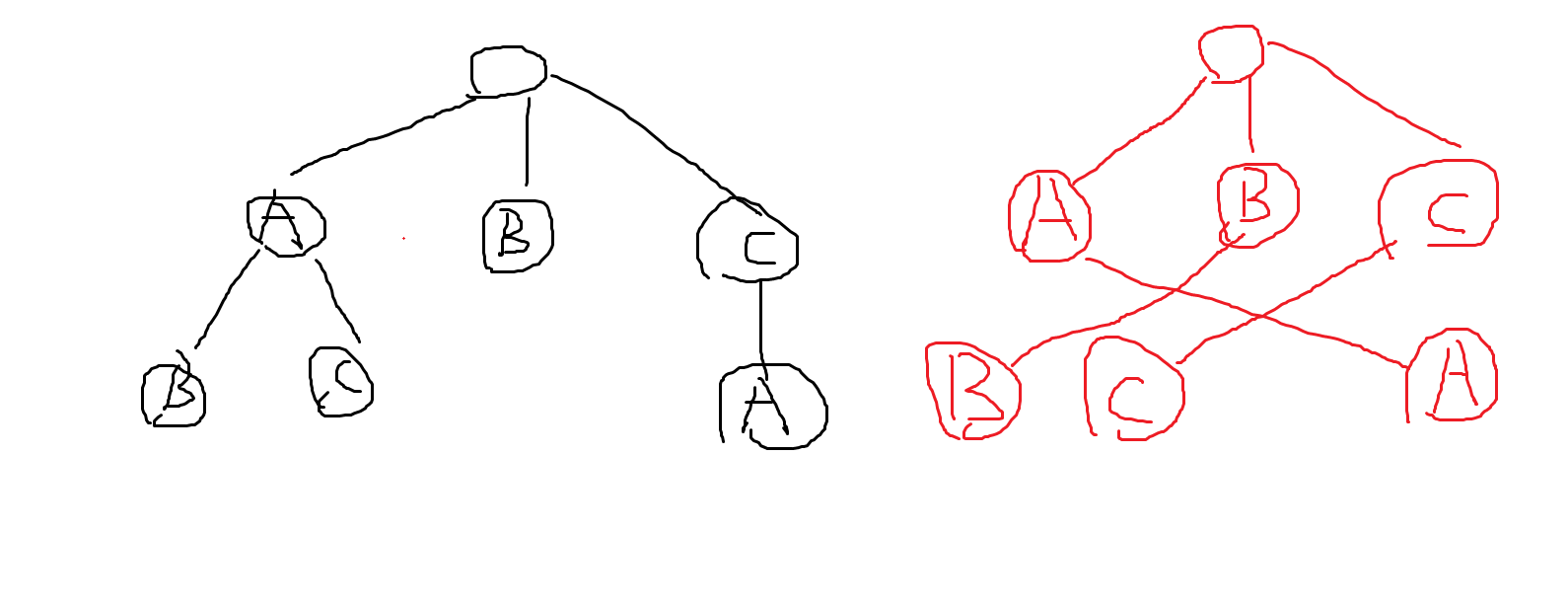
接着我们考虑先建出 \(AC\) 自动机：

小写字母，直接向下走。
P，存下这个点的编号。
B，回到父节点。

然后我们建出失配树。接着考虑怎么处理询问：

有多少个 \(x\) 在 \(y\) 中出现，事实上就是，有多少个 \(y\) 中的节点的 \(ne\) 指针直接或间接指向 \(x\) 的结束点。

于是我们对每个点 \(i\) 连一条 \(ne_i\rightarrow i\) 的边。如果 \(y\) 的一个点在 \(x\) 结束点为根的子树内，那么说明这个点的 \(ne\) 直接或间接指向 \(x\) 结束点。

所以我们把失配树做一个 \(dfs\) 序，使得一个点的子树变成一段区间，这就变成了一个单点修改，区间查询的问题。我们使用树状数组实现。

代码：

#include<bits/stdc++.h>
#define int long long
#define N 100005
using namespace std;
int n,m,tr[N][26],ne[N],idx;
int din[N],dout[N],res[N],sum,h[N];
int a[N],fa[N],tot;
string s;
struct edge{
	int to,nxt;
}e[N];
struct ask{
	int x,id;
};
vector<ask>q[N];
struct bit{
	int c[N];
	int lowbit(int x){
		return x&-x;
	}
	void modify(int x,int v){
		while(x<=sum){
			c[x]+=v;
			x+=lowbit(x);
		}
	}
	int qry(int x){
		int res=0;
		while(x){
			res+=c[x];
			x-=lowbit(x);
		}
		return res;
	}
}bits;
void add(int a,int b){
	e[++tot]={b,h[a]};
	h[a]=tot;
}
void ins(string s){
	int p=0;
	for(int i=0;s[i];i++){
		if(s[i]>='a'&&s[i]<='z'){
			int t=s[i]-'a';
			if(tr[p][t]==0){
				tr[p][t]=++idx;
				fa[tr[p][t]]=p;
			}
			p=tr[p][t];
		}
		else if(s[i]=='P')a[++n]=p;
		else p=fa[p];
	}
}
void dfs(int u,int f){
	din[u]=++sum;
	for(int i=h[u];i;i=e[i].nxt){
		int j=e[i].to;
		if(j==f)continue;
		dfs(j,u);
	}
	dout[u]=sum;
}
void build(){
	queue<int>q;
	for(int i=0;i<26;i++){
		if(tr[0][i]!=0){
			q.push(tr[0][i]);
		}
	}
	while(!q.empty()){
		int t=q.front();
		q.pop();
		for(int i=0;i<26;i++){
			int c=tr[t][i];
			if(c==0){
				tr[t][i]=tr[ne[t]][i];
			}
			else{
				ne[c]=tr[ne[t]][i];
				q.push(c);
			}
		}
	}
	for(int i=1;i<=idx;i++){
		add(ne[i],i);
	}
	dfs(0,0);
}
signed main(){
	cin>>s>>m;
	ins(s);
	build();
	for(int i=1;i<=m;i++){
		int x,y;
		cin>>x>>y;
		q[y].push_back({x,i});
	}
	int len=s.size();
	int id=0,p=0;
	for(int i=0;i<len;i++){
		if(s[i]>='a'&&s[i]<='z'){
			int t=s[i]-'a';
			p=tr[p][t];
			bits.modify(din[p],1);
		}
		else if(s[i]=='P'){
			id++;
			for(auto j:q[id]){
				int x=j.x,id=j.id;
				res[id]=bits.qry(dout[a[x]])-bits.qry(din[a[x]]-1);
			}
		}
		else{
			bits.modify(din[p],-1);
			p=fa[p];
		}
	}
	for(int i=1;i<=m;i++){
		cout<<res[i]<<'\n';
	}
	return 0;
}

posted @ 2024-07-30 00:28 zxh923 阅读(21) 评论(0) 收藏举报

刷新页面返回顶部

AC自动机 提高篇

文本生成器

数数

阿狸的打字机

公告

AC自动机提高篇