P4914 難題「龍の頸の玉 -五色の弾丸-」题解

P4914 難題「龍の頸の玉　-五色の弾丸-」

前置芝士：三角、反三角函数，正弦、余弦定理。

解法说明

根据题意，\(aa\) 发射的子弹有一个是背对辉夜的方向，其他龙玉发射方向与 \(aa\) 相同，可以发现无论五边形如何绕辉夜转，方向相对辉夜来说都是相同的，所以不需要 \(v\) 和 \(t\)。

五枚龙玉其中有两对龙玉是对称的，所以只需分讨三种情况。

1. \(aa\)

   因为有一发子弹背对辉夜，所以如果 \(k\) 是奇数，辉夜安全，反之危险。

2. 次外圈

   如下图，该三角形两边已确定。因为正五边形，故 \(r\) 与 \(R\) 夹角为 \(\frac{2\pi}{5}\)。通过余弦定理解出辉夜与龙玉的距离，再用正弦定理解出角 \(\theta\)，通过 \(k\) 算出两发子弹间隔，检验间隔是否整除角 \(\theta\) 即可。

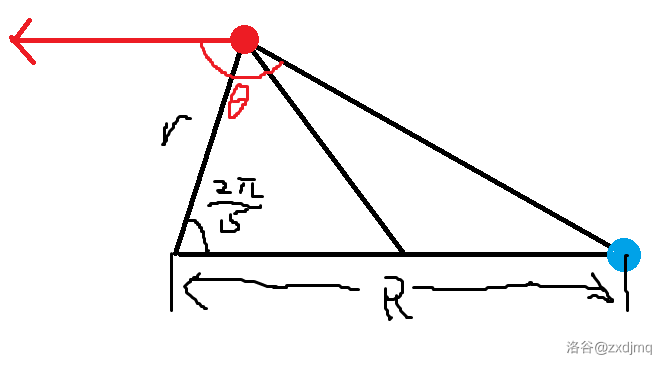
最外圈的解法与次外圈同理，只需把 \(\frac{2\pi}{5}\) 改为 \(\frac{4\pi}{5}\)。

单次询问时间复杂度为 \(O(1)\)。

代码

Code (C++)

#include<bits/stdc++.h>
using namespace std;
#define ld long double
#define int long long
const ld pi=acos(-1.0);
const ld inf=1e-10;
ld r,R,v,t;
int T,k;
signed main(){
    ios::sync_with_stdio(0);
    cin.tie(nullptr);
    cin>>T;
    while(T--){
        cin>>r>>R>>v>>t>>k;
        if((k&1)==0){cout<<"no\n";continue;}
        ld xi=r*r+R*R-2*r*R*cos(pi*0.4);
        ld ang=pi-asin(sin(pi*0.4)/xi*r);
        ld ans=ang/(2*pi/k);
        if(ceil(ans)-ans<inf){cout<<"no\n";continue;}
        xi=r*r+R*R-2*r*R*cos(pi*0.8);
        ang=pi-asin(sin(pi*0.8)/xi*r);
        ans=ang/(2*pi/k);
        if(ceil(ans)-ans<inf){cout<<"no\n";continue;}
        cout<<"yes\n";
    }
    return 0;
}