【pytorch学习】之概率

6 概率

简单地说，机器学习就是做出预测。根据病人的临床病史，我们可能想预测他们在下一年心脏病发作的概率。在飞机喷气发动机的异常检测中，我们想要评估一组发动机读数为正常运行情况的概率有多大。在强化学习中，我们希望智能体（agent）能在一个环境中智能地行动。这意味着我们需要考虑在每种可行的行为下获得高奖励的概率。当我们建立推荐系统时，我们也需要考虑概率。例如，假设我们为一家大型在线书店工作，我们可能希望估计某些用户购买特定图书的概率。为此，我们需要使用概率学。有完整的课程、专业、论文、职业、甚至院系，都致力于概率学的工作。所以很自然地，我们在这部分的目标不是教授整个科目。相反，我们希望教给读者基础的概率知识，使读者能够开始构建第一个深度学习模型，以便读者可以开始自己探索它。
现在让我们更认真地考虑第一个例子：根据照片区分猫和狗。这听起来可能很简单，但对于机器却可能是一个艰巨的挑战。首先，问题的难度可能取决于图像的分辨率。

虽然人类很容易以160 × 160像素的分辨率识别猫和狗，但它在40 × 40像素上变得具有挑战性，而且在10 × 10像素下几乎是不可能的。换句话说，我们在很远的距离（从而降低分辨率）区分猫和狗的能力可能会变为猜测。概率给了我们一种正式的途径来说明我们的确定性水平。如果我们完全肯定图像是只猫，我们说标签y是“猫”的概率，表示为P(y =“猫”)等于1。如果我们没有证据表明y =“猫”或y =
“狗”，那么我们可以说这两种可能性是相等的，即\(P(y ='猫') = P(y ='狗') = 0.5\)。如果我们不十分确定图像描绘的是一只猫，我们可以将概率赋值为0.5 < P(y =“猫”) < 1。
现在考虑第二个例子：给出一些天气监测数据，我们想预测明天北京下雨的概率。如果是夏天，下雨的概率为0.5。
在这两种情况下，我们都不确定结果，但这两种情况之间有一个关键区别。在第一种情况中，图像实际上是狗或猫二选一。在第二种情况下，结果实际上是一个随机的事件。因此，概率是一种灵活的语言，用于说明我们的确定程度，并且它可以有效地应用于广泛的领域中。

6.1 基本概率论

假设我们掷骰子，想知道看到1的几率有多大，而不是看到另一个数字。如果骰子是公平的，那么所有六个结果\({1, . . . , 6}\)都有相同的可能发生，因此我们可以说1发生的概率为\(\frac{1}{6}\)。
然而现实生活中，对于我们从工厂收到的真实骰子，我们需要检查它是否有瑕疵。检查骰子的唯一方法是多次投掷并记录结果。对于每个骰子，我们将观察到{1, . . . , 6}中的一个值。对于每个值，一种自然的方法是将它出现的次数除以投掷的总次数，即此事件（event）概率的估计值。大数定律（law of large numbers）告诉我们：随着投掷次数的增加，这个估计值会越来越接近真实的潜在概率。让我们用代码试一试！
首先，我们导入必要的软件包。

%matplotlib inline
import torch
from torch.distributions import multinomial
from d2l import torch as d2l

在统计学中，我们把从概率分布中抽取样本的过程称为抽样（sampling）。笼统来说，可以把分布（distribution）看作对事件的概率分配，稍后我们将给出的更正式定义。将概率分配给一些离散选择的分布称为多项分布（multinomial distribution）。为了抽取一个样本，即掷骰子，我们只需传入一个概率向量。输出是另一个相同长度的向量：它在索引i处的值是采样结果中i出现的次数。

fair_probs = torch.ones([6]) / 6
multinomial.Multinomial(1, fair_probs).sample()

tensor([0., 0., 1., 0., 0., 0.])

在估计一个骰子的公平性时，我们希望从同一分布中生成多个样本。如果用Python的for循环来完成这个任务，速度会慢得惊人。因此我们使用深度学习框架的函数同时抽取多个样本，得到我们想要的任意形状的独立样本数组。

multinomial.Multinomial(10, fair_probs).sample()

tensor([1., 0., 1., 2., 5., 1.])

现在我们知道如何对骰子进行采样，我们可以模拟1000次投掷。然后，我们可以统计1000次投掷后，每个数字被投中了多少次。具体来说，我们计算相对频率，以作为真实概率的估计。

# 将结果存储为32位浮点数以进行除法
counts = multinomial.Multinomial(1000, fair_probs).sample()
counts / 1000 # 相对频率作为估计值

tensor([0.1600, 0.1810, 0.1420, 0.1480, 0.1970, 0.1720])

因为我们是从一个公平的骰子中生成的数据，我们知道每个结果都有真实的概率\(\frac{1}{6}\)，大约是0.167，所以上面输出的估计值看起来不错。

我们也可以看到这些概率如何随着时间的推移收敛到真实概率。让我们进行500组实验，每组抽取10个样本。

counts = multinomial.Multinomial(10, fair_probs).sample((500,))
cum_counts = counts.cumsum(dim=0)
estimates = cum_counts / cum_counts.sum(dim=1, keepdims=True)
d2l.set_figsize((6, 4.5))
for i in range(6):
    d2l.plt.plot(estimates[:, i].numpy(),label=("P(die=" + str(i + 1) + ")"))
d2l.plt.axhline(y=0.167, color='black', linestyle='dashed')
d2l.plt.gca().set_xlabel('Groups of experiments')
d2l.plt.gca().set_ylabel('Estimated probability')
d2l.plt.legend();

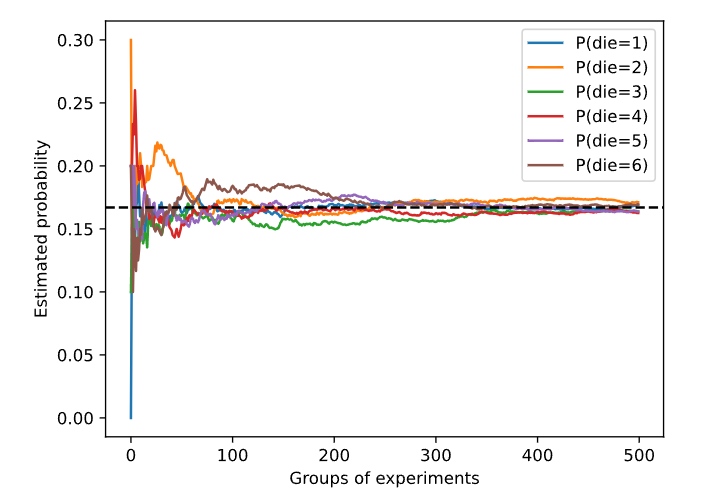
每条实线对应于骰子的6个值中的一个，并给出骰子在每组实验后出现值的估计概率。当我们通过更多的实验获得更多的数据时，这6条实体曲线向真实概率收敛。
概率论公理
在处理骰子掷出时，我们将集合S = {1, 2, 3, 4, 5, 6} 称为样本空间（sample space）或结果空间（outcomespace），其中每个元素都是结果（outcome）。事件（event）是一组给定样本空间的随机结果。例如，“看到5”（{5}）和“看到奇数”（{1, 3, 5}）都是掷出骰子的有效事件。注意，如果一个随机实验的结果在A中，则事件A已经发生。也就是说，如果投掷出3点，因为3 ∈ {1, 3, 5}，我们可以说，“看到奇数”的事件发生了。概率（probability）可以被认为是将集合映射到真实值的函数。在给定的样本空间S中，事件A的概率，表示为\(P(A)\)，满足以下属性
对于任意事件A，其概率从不会是负数，即P(A) ≥ 0；
整个样本空间的概率为1，即P(S) = 1；
对于互斥（mutually exclusive）事件（对于所有 \(( i \neq j )\)，有 \(( A_i \cap A_j = \emptyset )\)的任意一个可数序列\(A_1, A_2, . . .，\)序列中任意一个事件发生的概率等于它们各自发生的概率之和，即\(P(\cup_{i=1}^{\infty} A_i) = \sum_{i=1}^{\infty} P(A_i)\)。
以上也是概率论的公理，由科尔莫戈罗夫于1933年提出。有了这个公理系统，我们可以避免任何关于随机性的哲学争论；相反，我们可以用数学语言严格地推理
随机变量
在我们掷骰子的随机实验中，我们引入了随机变量（random variable）的概念。随机变量几乎可以是任何数量，并且它可以在随机实验的一组可能性中取一个值。考虑一个随机变量X，其值在掷骰子的样本空间S = {1, 2, 3, 4, 5, 6}中。我们可以将事件“看到一个5”表示为{X = 5}或X = 5，其概率表示为P({X =5})或P(X = 5)。通过P(X = a)，我们区分了随机变量X和X可以采取的值（例如a）。然而，这可能会导致繁琐的表示。为了简化符号，一方面，我们可以将P(X)表示为随机变量X上的分布（distribution）：分布告诉我们X获得某一值的概率。另一方面，我们可以简单用P(a)表示随机变量取值a的概率。由于概率论中的事件是来自样本空间的一组结果，因此我们可以为随机变量指定值的可取范围。例如，P(1 ≤ X ≤ 3)表示事件{1 ≤ X ≤ 3}，即{X = 1, 2, or, 3}的概率。等价地，P(1 ≤ X ≤ 3)表示随机变量X从{1, 2, 3}中取值的概率。
请注意，离散（discrete）随机变量（如骰子的每一面）和连续（continuous）随机变量（如人的体重和身高）之间存在微妙的区别。现实生活中，测量两个人是否具有完全相同的身高没有太大意义。如果我们进行足够精确的测量，最终会发现这个星球上没有两个人具有完全相同的身高。在这种情况下，询问某人的身高是否落入给定的区间，比如是否在1.79米和1.81米之间更有意义。在这些情况下，我们将这个看到某个数值的可能性量化为密度（density）。高度恰好为1.80米的概率为0，但密度不是0。在任何两个不同高度之间的区间，我们都有非零的概率。

6.2 处理多个随机变量

很多时候，我们会考虑多个随机变量。比如，我们可能需要对疾病和症状之间的关系进行建模。给定一个疾病和一个症状，比如“流感”和“咳嗽”，以某个概率存在或不存在于某个患者身上。我们需要估计这些概率以及概率之间的关系，以便我们可以运用我们的推断来实现更好的医疗服务。
再举一个更复杂的例子：图像包含数百万像素，因此有数百万个随机变量。在许多情况下，图像会附带一个标签（label），标识图像中的对象。我们也可以将标签视为一个随机变量。我们甚至可以将所有元数据视为随机变量，例如位置、时间、光圈、焦距、ISO、对焦距离和相机类型。所有这些都是联合发生的随机变量。当我们处理多个随机变量时，会有若干个变量是我们感兴趣的。
联合概率
第一个被称为联合概率（joint probability）P(A = a, B = b)。给定任意值a和b，联合概率可以回答：\(A =a\)和\(B = b\)同时满足的概率是多少？请注意，对于任何a和b的取值，P(A = a, B = b) ≤ P(A = a)。这点是确定的，因为要同时发生\(A = a\)和\(B = b\)，\(A = a\)就必须发生，\(B = b\)也必须发生（反之亦然）。因此，\(A = a\)和\(B = b\)同时发生的可能性不大于\(A = a\)或是$ = b$独发生的可能性。
条件概率
联合概率的不等式带给我们一个有趣的比率：\(0<\text{比率} = \frac{P(B = b | A = a)}{P(B = b)} <1\)我们称这个比率为条件概率（conditionalprobability），并用\(P(B = b | A = a) = \frac{P(A = a, B = b)}{P(A = a)}\)表示它：它是B = b的概率，前提是A = a已发生。
贝叶斯定理
使用条件概率的定义，我们可以得出统计学中最有用的方程之一：Bayes定理（Bayes’theorem）。根据乘法法则（multiplication rule )可得到\(P(A, B) = P(B | A)P(A)\),根据对称性，可得到\(P(A, B) = P(A | B)P(B)\)。
假设P(B) > 0，求解其中一个条件变量，我们得到$$P(A | B) = \frac{P(B | A) \times P(A)}{P(B)}$$

请注意，这里我们使用紧凑的表示法：其中P(A, B)是一个联合分布（joint distribution），\(P(A | B)\)是一个条件分布（conditional distribution）。这种分布可以在给定值A = a, B = b上进行求值。
边际化
为了能进行事件概率求和，我们需要求和法则（sum rule），即B的概率相当于计算A的所有可能选择，并将所有选择的联合概率聚合在一起：

\[P(A, B) = \sum_{\text A} P(B | A) \]

这也称为边际化（marginalization）。边际化结果的概率或分布称为边际概率（marginalprobability）或边际分布（marginal distribution）。
独立性
另一个有用属性是依赖（dependence）与独立（independence）。如果两个随机变量A和B是独立的，意味着事件A的发生跟B事件的发生无关。在这种情况下，统计学家通常将这一点表述为A ⊥ B。根据贝叶斯定理，马上就能同样得到P(A | B) = P(A)。在所有其他情况下，我们称A和B依赖。比如，两次连续抛出一个骰子的事件是相互独立的。相比之下，灯开关的位置和房间的亮度并不是（因为可能存在灯泡坏掉、电源故障，或者开关故障）。
由于P$ P(A | B) = \frac{P(B | A) \times P(A)}{P(B)}$ 等价于 $ P(A, B) = P(A) \times P(B) $因此两个随机变量是独立的，当且仅当两个随机变量的联合分布是其各自分布的乘积。同样地，给定另一个随机变量C时，两个随机变量A和B是条件独立的（conditionally independent）.
整：
根据贝叶斯定理，我们有：

$ P(A | B) = \frac{P(B | A) \times P(A)}{P(B)} $
如果我们将 $( P(A | B) $ 用 \(( P(A, B) )\) 表示，那么有：
$ P(A, B) = \frac{P(B | A) \times P(A)}{P(B)} $

进一步，如果$ P(A, B) = P(A) \times P(B) $，那么：

\[P(A) \times P(B) = \frac{P(B | A) \times P(A)}{P(B)} \]

如果我们将 $ P(B) $ 乘到等式的两侧，我们得到：

\[P(A) \times P(B) \times P(B) = P(B | A) \times P(A) \]

简化后得到：

\[P(B) \times P(A) = P(B | A) \times P(A) \]

这与原先的贝叶斯定理相符，所以 $ P(A, B) = P(A) \times P(B) $是贝叶斯定理的一个等价形式。

6.3 期望和方差

为了概括概率分布的关键特征，我们需要一些测量方法。一个随机变量X的期望（expectation，或平均值（average））表示为

\[E[X] = \sum_{i=1}^{n} x_i \times P(X = x_i) \]

当函数f(x)的输入是从分布P中抽取的随机变量时，f(x)的期望值为$$E_X \sim P[f(x)] = \sum_{x} f(x) \cdot P(x)$$
在许多情况下，我们希望衡量随机变量X与其期望值的偏置。这可以通过方差来量化

\[\text{Var}[X] = E[X^2] - (E[X])^2 \]