1.12练习

“快过年了，你可不能像邻家哥哥天天坐在电脑面前写不知道是啥的玩意”

原题地址https://www.luogu.com.cn/problem/P1064

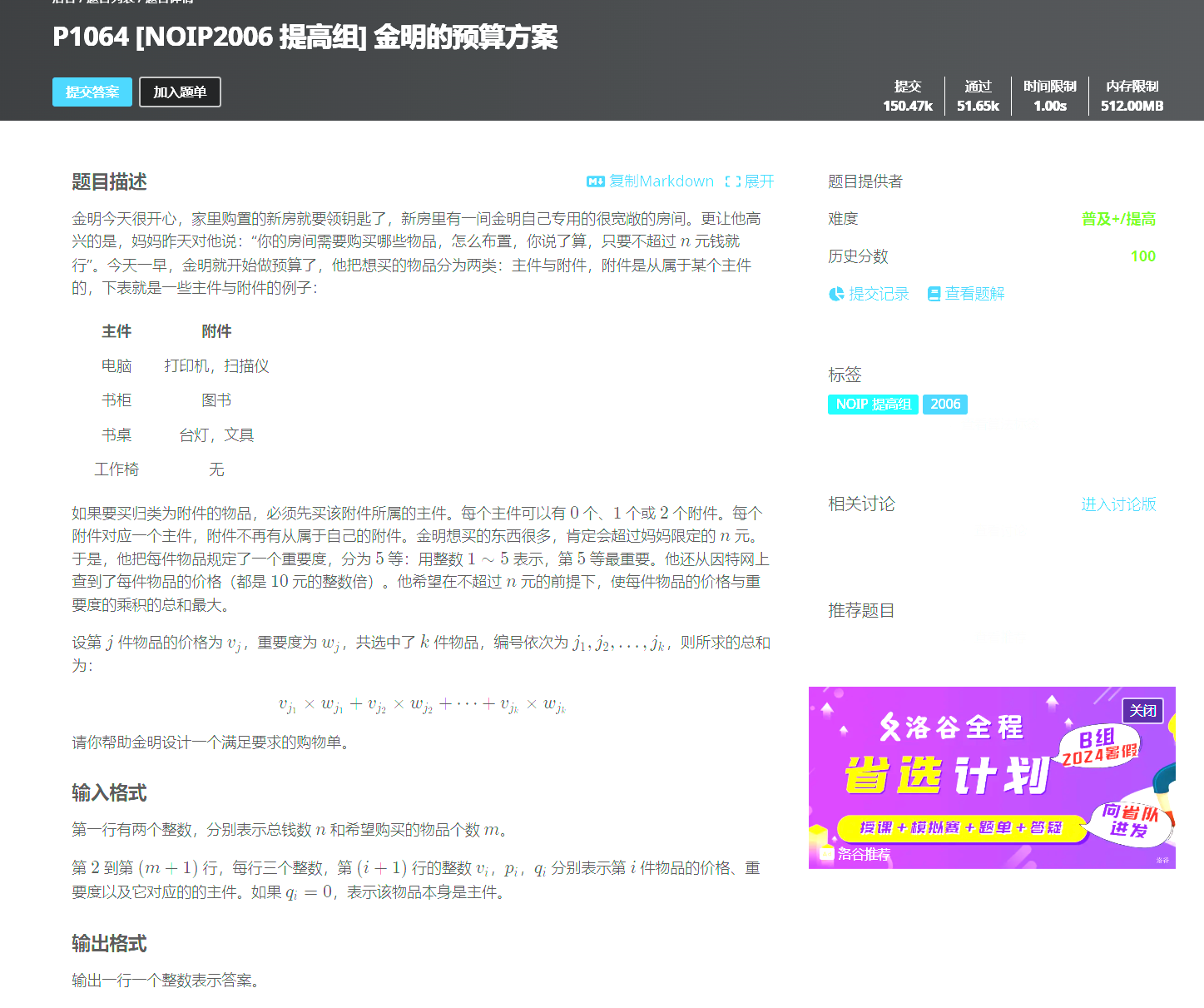
这个题目是一个背包dp问题，准确来说是01背包的变种。该题中商品只有买和不买两种判断，但是其中有部分商品必须在先买其他商品的前提下才能去购买。题意是每件物品都有一个价格和重要度，在预算为n元的情况下要使购买的物品的价格和重要度的乘积最大。同时物品分为主件和附件，购买附件就必须先购买附件对应的主件。所以可以先建立一个结构体动态数组用来表示价格和重要度，即：

戳这个

struct op{
	int v,p;
	//v为价格，p为重要度
};

以及：

戳这个

int n,m;
cin>>n>>m;
vector<op> zj(m+1);//主件的重量和价值
vector<op> fj1(m+1,{0,0}); //主件对应附件1，2的重量和价值
vector<op> fj2(m+1,{0,0});

其中n代表马内，也就是预算，而m代表商品的件数。
然后通过一个for循环来输入每个商品的价格，重要度，以及判断该商品是主件还是附件，是附件的话对应哪一个商品。由此可得：

戳这个

for(int i=1;i<=m;i++){
	int a,b,c;
	cin>>a>>b>>c;  //当c为0时输入主件，反之则输入附件
	if (c == 0){
	    zj[i].v=a;
	    zj[i].p=b; 
	} else if(fj1[c].v==0){ 
	    fj1[c].v=a;
	    fj1[c].p=b; 
	} else{ 
	    fj2[c].v=a;
	    fj2[c].p=b; 
	}
}

接下来对动态规划进行初始化：vector dp (n+1,0);
现在我们已经完成了基本数据的输入和动态规划的初始化。接下来进行动态规划的计算。为了遍历完所有主件，我们需要遍历m次，此时可能会超出存在的主件的范围，因此用if (zj[i].v==0) continue来跳过它们。然后接下来通过嵌套循环对主件，主件+附件1，主件+附件2，主件+附件1+附件2等四种情况进行判断（感谢龙哥帮我检查出来我少判断了一种条件），判断购买哪种组合的乘积最大，能得到以下状态转移方程：

1.只购买主件 𝑑𝑝[𝑗]=max⁡(𝑑𝑝[𝑗],𝑑𝑝[𝑗−𝑧𝑗[𝑖].𝑣]+𝑧𝑗[𝑖].𝑣×𝑧𝑗[𝑖].𝑝)
2.主件+附件1 𝑑𝑝[𝑗]=max⁡(𝑑𝑝[𝑗],𝑑𝑝[𝑗−𝑧𝑗[𝑖].𝑣−𝑓𝑗1[𝑖].𝑣]+𝑧𝑗[𝑖].𝑣×𝑧𝑗[𝑖].𝑝+𝑓𝑗1[𝑖].𝑣×𝑓𝑗1[𝑖].𝑝)
3.主件＋附件2 𝑑𝑝[𝑗]=max⁡(𝑑𝑝[𝑗],𝑑𝑝[𝑗−𝑧𝑗[𝑖].𝑣−𝑓𝑗2[𝑖].𝑣]+𝑧𝑗[𝑖].𝑣×𝑧𝑗[𝑖].𝑝+𝑓𝑗2[𝑖].𝑣×𝑓𝑗2[𝑖].𝑝)
4主件+附件1，2 𝑑𝑝[𝑗]=max⁡(𝑑𝑝[𝑗],𝑑𝑝[𝑗−𝑧𝑗[𝑖].𝑣−𝑓𝑗1[𝑖].𝑣−𝑓𝑗2[𝑖].𝑣]+𝑧𝑗[𝑖].𝑣×𝑧𝑗[𝑖].𝑝+𝑓𝑗1[𝑖].𝑣×𝑓𝑗1[𝑖].𝑝+𝑓𝑗2[𝑖].𝑣×𝑓𝑗2[𝑖].𝑝)

此时能得到以下代码：

还是戳这个

for(int i=1;i<=m;i++){    //动态规划
	if (zj[i].v==0) continue;  //主件的价值为0时说明不存在该主件，需要跳过
	for(int j=n;j>=0;j--){    //状态转移方程，主件，主件+附件1，主件+附件2，主件+附件1、2；
		if(j>=zj[i].v){
			dp[j]=max(dp[j],dp[j-zj[i].v]+zj[i].v*zj[i].p);
		}
		if(j>=zj[i].v+fj1[i].v){
			dp[j]=max(dp[j],dp[j-zj[i].v-fj1[i].v]+zj[i].v*zj[i].p+fj1[i].v*fj1[i].p);
		}
		if(j>=zj[i].v+fj2[i].v){
		 	dp[j]=max(dp[j],dp[j-zj[i].v-fj2[i].v]+zj[i].v*zj[i].p+fj2[i].v*fj2[i].p);
		}
		if(j>=zj[i].v+fj1[i].v+fj2[i].v){
			dp[j]=max(dp[j],dp[j-zj[i].v-fj1[i].v-fj2[i].v]+zj[i].v*zj[i].p+fj1[i].v*fj1[i].p+fj2[i].v*fj2[i].p);
		}
	}
}

最后输出在预算内可以达到的最大重要度，即dp[n]。
完整代码如下：

点击查看代码

#include <bits/stdc++.h>
using namespace std;
struct op{
	int v,p;
	//v为价格，p为重要度
};
int main()
{
	int n,m;
	cin>>n>>m;
	vector<op> zj(m+1);//主件的重量和价值
	vector<op> fj1(m+1,{0,0}); //主件对应附件1，2的重量和价值
	vector<op> fj2(m+1,{0,0});
	for(int i=1;i<=m;i++){
		int a,b,c;
		cin>>a>>b>>c;  //当c为0时输入主件，反之则输入附件
		if (c==0){
		    zj[i].v=a;
		    zj[i].p=b; 
		} else if(fj1[c].v==0){ 
		    fj1[c].v=a;
		    fj1[c].p=b; 
		} else{ 
		    fj2[c].v=a;
		    fj2[c].p=b; 
		}
	}
	vector <int> dp (n+1,0);  //动态规划初始化
	for(int i=1;i<=m;i++){    //动态规划
		if (zj[i].v==0) continue;  //主件的价值为0时说明不存在该主件，需要跳过
		for(int j=n;j>=0;j--){    //状态转移方程，主件，主件+附件1，主件+附件2，主件+附件1、2；
			if(j>=zj[i].v){
				dp[j]=max(dp[j],dp[j-zj[i].v]+zj[i].v*zj[i].p);
			}
			if(j>=zj[i].v+fj1[i].v){
				dp[j]=max(dp[j],dp[j-zj[i].v-fj1[i].v]+zj[i].v*zj[i].p+fj1[i].v*fj1[i].p);
			}
			if(j>=zj[i].v+fj2[i].v){
			 	dp[j]=max(dp[j],dp[j-zj[i].v-fj2[i].v]+zj[i].v*zj[i].p+fj2[i].v*fj2[i].p);
			}
			if(j>=zj[i].v+fj1[i].v+fj2[i].v){
				dp[j]=max(dp[j],dp[j-zj[i].v-fj1[i].v-fj2[i].v]+zj[i].v*zj[i].p+fj1[i].v*fj1[i].p+fj2[i].v*fj2[i].p);
			}
		}
	}
	cout<<dp[n]<<endl; // 输出在预算内可以达到的最大重要度
	return 0;
}

这样就能ac了。