机器学习-监督学习之降维算法（PCA）

一、降维算法概述

1.降维算法概述
　　降维就是一种针对高维度特征进行的数据预处理方法，是应用非常广泛的数据预处理方法。
　　降维算法指对高维度的数据保留下最重要的一些特征，去除噪声和不重要的特征，从而实现提升数据处理速度的目的。在实际的生产和应用中，在一定的信息损失范围内，降维可以节省大量的时间和成本。
　　机器学习领域中所谓的降维就是指采用某种映射方法，将原高维空间中的数据点映射到低维度的空间中。
2.降维算法的分类
主成分分析（Principal Component Analysis，PCA）法
　　试图在保证数据信息丢失最少的原则下，对多个变量进行最佳综合简化，即对高维变量空间进行降维处理。
因子分析（Factor Analysis，FA）法
　　因子分析法是从假设出发。
因子分析法有几个主要目的：一是进行结构的探索，在变量之间存在高度相关性的时候希望用较少的因子来概括其信息；二是把原始变量转换为因子得分后，使用因子得分进行其他分析，从而简化数据，如聚类分析、回归分析等；三是通过每个因子得分计算出综合得分，对分析对象进行综合评价。
3.降维算法的应用场景
　　降维算法通常应用于数据压缩与数据可视化中。

二、数据降维

数据降维(Dimensionality Reduction)：

数据降维案例(经济分析):

任务(真实事件):通过美国1929-1938年各年经济数据，预测国民收入与支出

数据包括:雇主补贴、消费资料和生产资料、纯公共支出、净增库存、股息、利息、外贸平衡等十七个指标

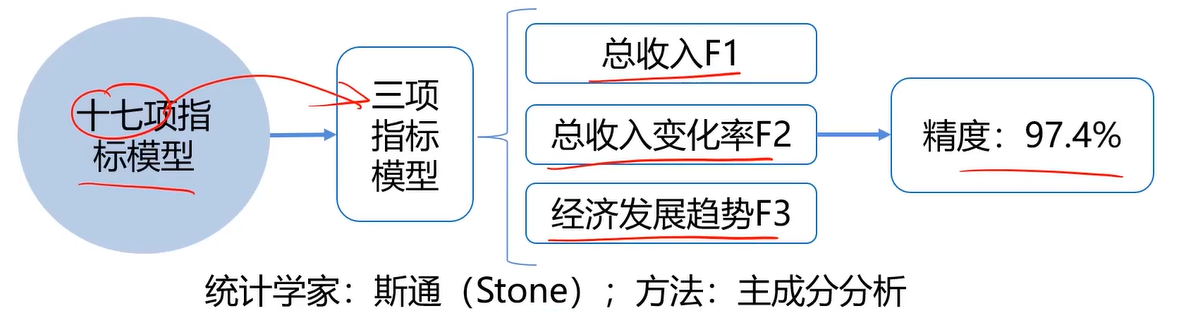
数据降维，是指在某些限定条件下，降低随机变量个数，得到一组“不相关”主变量的过程。

作用:减少模型分析数据量，提升处理效率，降低计算难度，实现数据可视化。

数据量下降举例:2D数据降维到1D数据

将二维数据投影到一条直线上面

数据量下降举例:3D数据降维到2D数据

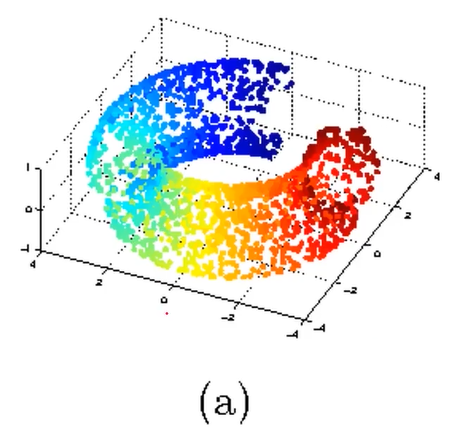
投影之后变成二维数据

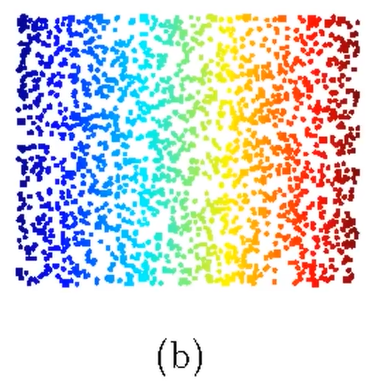
数据可视化举例:国家分布可视化(基于50项经济指标)

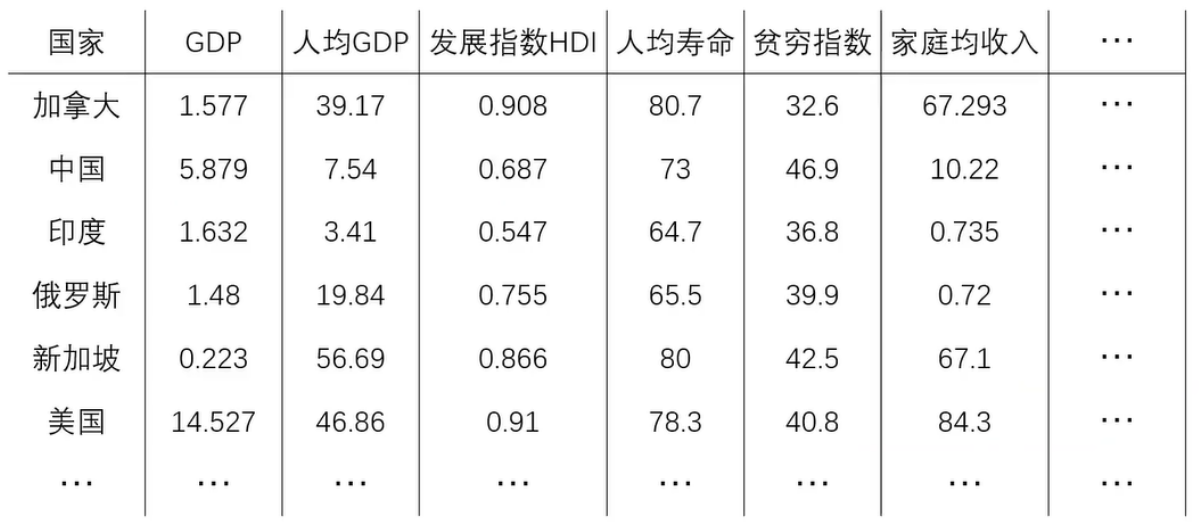
缩减为两项指标：复合指标F1和复合指标F2

这样就可以进行可视化展示：

三、主成分分析(PCA)

数据降维的实现:主成分分析(PCA)

PCA(principal components analysis):数据降维技术中，应用最最多的方法

目标:寻找k(k<n)维新数据，使它们反映事物的主要特征

核心:在信息损失尽可能少的情况下，降低数据维度。

二维数据PCA

三维数据PCA

 

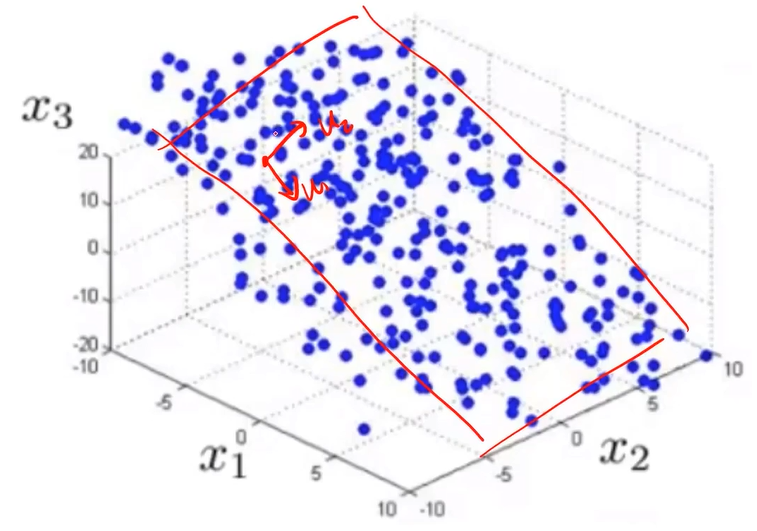
3D到2D:投影到u₁、u₂形成的平面

n维到k维：投影到u₁、u₂...u_k形成的空间

如何保留主要信息:

投影后的不同特征数据尽可能分得开(即不相关)

如何实现?

使投影后数据的方差最大，因为方差越大数据也越分散。

计算过程

（1）、原始数据预处理(标准化:μ=0,σ=1)，即将N维数据实现标准正态分布，即处理后均值为0，方差为1。

（2）、计算协方差矩阵特征向量、及数据在各特征向量投影后的方差，方差越大，相关性越小，将方差小的舍弃掉。

（3）、根据需求(任务指定或方差比例)确定降维维度k

（4）、选取k维特征向量，计算数据在其形成空间的投影

三、实战-PCA(iris数据降维后分类)

数据集

1、基于iris_data.csv数据，建立KNN模型实现数据分类(n_neighbors=3)

2、对数据进行标准化处理，选取一个维度可视化处理后的效果

3、进行与原数据等维度PCA，查看各主成分的方差比例

4、保留合适的主成分，可视化降维后的数据

5、基于降维后数据建立KNN模型，与原数据表现进行对比

1、加载数据

#加载数据
import torch
import pandas as pd
import numpy as np
from sklearn.metrics import accuracy_score
# from matplotlib import pyplot as plt
import matplotlib
matplotlib.use('TkAgg')
import matplotlib.pyplot as plt

data = pd.read_csv('./data/iris_data.csv')
print(data)

结果：

     sepal length  sepal width  ...          target  label
0             5.1          3.5  ...     Iris-setosa      0
1             4.9          3.0  ...     Iris-setosa      0
2             4.7          3.2  ...     Iris-setosa      0
3             4.6          3.1  ...     Iris-setosa      0
4             5.0          3.6  ...     Iris-setosa      0
..            ...          ...  ...             ...    ...
145           6.7          3.0  ...  Iris-virginica      2
146           6.3          2.5  ...  Iris-virginica      2
147           6.5          3.0  ...  Iris-virginica      2
148           6.2          3.4  ...  Iris-virginica      2
149           5.9          3.0  ...  Iris-virginica      2

2、定义X和y

#定义X,y
X = data.drop(['target','label'],axis=1) # 去掉最后两列
y = data.loc[:,'label']
print(X.shape,y.shape)#打印X，y的维度

结果：(150, 4) (150,)

3、建立KNN模型实现数据分类(n_neighbors=3)

选用最近的3个点来预测新的点属于哪一类

#建立KNN模型
from sklearn.neighbors import KNeighborsClassifier
KNN = KNeighborsClassifier(n_neighbors=3)
KNN.fit(X,y) # 训练
# 预测
y_predict = KNN.predict(X)
# 计算准确率
accuracy = accuracy_score(y,y_predict)
print(accuracy)

结果：0.96

第一步已经完成，接下来进入第二步：对数据进行标准化处理，选取一个维度可视化处理后的效果

4、对数据进行标准化处理

# 对数据进行标准化处理
from sklearn.preprocessing import StandardScaler
X_norm = StandardScaler().fit_transform(X)
print(X_norm)

结果：

[[-9.00681170e-01  1.03205722e+00 -1.34127240e+00 -1.31297673e+00]
 [-1.14301691e+00 -1.24957601e-01 -1.34127240e+00 -1.31297673e+00]
 [-1.38535265e+00  3.37848329e-01 -1.39813811e+00 -1.31297673e+00]
 ......
 [ 1.03800476e+00 -1.24957601e-01  8.19624347e-01  1.44795564e+00]
 [ 5.53333275e-01 -1.28197243e+00  7.05892939e-01  9.22063763e-01]
 [ 7.95669016e-01 -1.24957601e-01  8.19624347e-01  1.05353673e+00]
 [ 4.32165405e-01  8.00654259e-01  9.33355755e-01  1.44795564e+00]
 [ 6.86617933e-02 -1.24957601e-01  7.62758643e-01  7.90590793e-01]]

5、选取一个维度（sepal length）计算均值和方差

# 计算均值和方差
x1_mean = X.loc[:,"sepal length"].mean()
x1_sigma = X.loc[:,"sepal length"].std()
x1_norm_mean = X_norm[:,0].mean()
x1_norm_sigma = X_norm[:,0].std()
print(x1_mean,x1_sigma,x1_norm_mean,x1_norm_sigma)

结果：

5.843333333333334 0.8280661279778629 -4.736951571734001e-16 1.0

x1_norm_mean的值为-4.736951571734001e-16，相当于0了。

6、选取一个维度，可视化处理后的效果

# 选取一个维度，可视化处理后的效果
fig1 = plt.figure(figsize=(20, 5))
# 原来的数据分布
plt.subplot(121)
plt.hist(X.loc[:,"sepal length"],bins=100)
# 标准化处理之后的数据
plt.subplot(122)
plt.hist(X_norm[:,0],bins=100)
plt.show()

结果：

发现原来的sepal length这个维度的均值在6左右，标准化处理之后变为了0左右。

到这里第二步已经完成，现在来看第三步：进行与原数据等维度PCA，查看各主成分的方差比例

7、进行与原数据等维度PCA

# 进行与原数据等维度PCA，查看各主成分的方差比例
print(X.shape) # (150,4) 即原数据的维度为4
from sklearn.decomposition import PCA
pca = PCA(n_components=4) # 同等维度处理
# 等维度PCA后的数据x_pca
x_pca = pca.fit_transform(X_norm) # 参数为标准化处理之后的数据X_norm
print(x_pca)

结果:

[[-2.26454173e+00  5.05703903e-01  1.21943348e-01 -2.30733235e-02]
 [-2.08642550e+00 -6.55404729e-01  2.27250832e-01 -1.03208244e-01]
 [-2.36795045e+00 -3.18477311e-01 -5.14796236e-02 -2.78252250e-02]
 [-2.30419716e+00 -5.75367713e-01 -9.88604444e-02  6.63114622e-02]
  ......
 [ 1.55849189e+00 -9.05313601e-01  2.53819099e-02 -2.21322184e-01]
 [ 1.52084506e+00  2.66794575e-01 -1.79277203e-01 -1.18903043e-01]
 [ 1.37639119e+00  1.01636193e+00 -9.31405052e-01 -2.41461953e-02]
 [ 9.59298576e-01 -2.22839447e-02 -5.28794187e-01  1.63675806e-01]]

8、查看各主成分的方差比例

# 计算每个主成分的方差比例
var_ratio = pca.explained_variance_ratio_
print(var_ratio) # [0.72770452 0.23030523 0.03683832 0.00515193]

9、可视化各主成分的方差比例

# 可视化方差比例
fig2 = plt.figure(figsize=(20,5))
plt.bar([1, 2, 3, 4],var_ratio)
plt.xticks([1, 2, 3, 4],['PC1', 'PC2', 'PC3', 'PC4'])
plt.ylabel("variance ratio of each principle components")
plt.show()

结果：

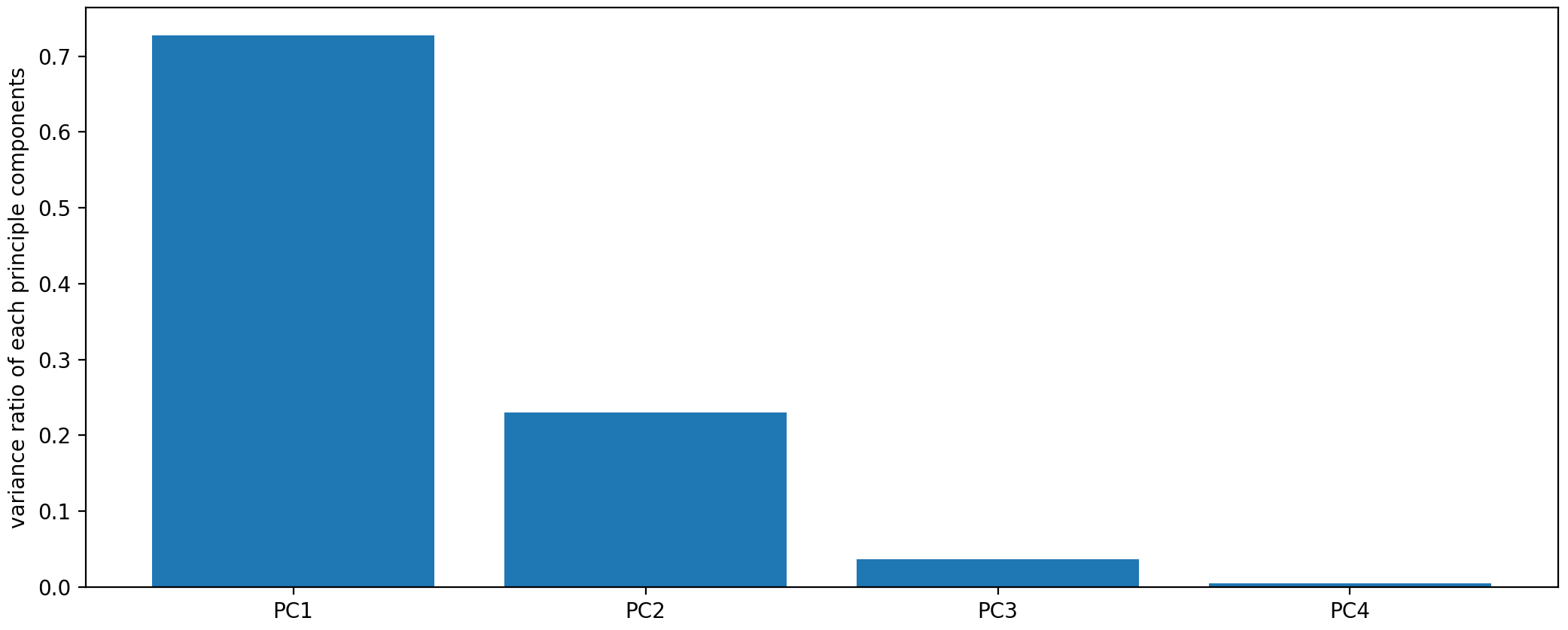
发现前面两个主成分的方差比例比较大， 后面两个比较小。

至此，第三步已经完成，现在来看第四步：保留合适的主成分，可视化降维后的数据

10、保留合适的主成分，只需要保留前面两个成分

pca = PCA(n_components=2) # 只需要保留前面两个成分 即开始降维
X_pca = pca.fit_transform(X_norm) # 降维后的数据
print(X_pca) # 4维数据变为2维数据
print(X_pca.shape) # （150，2）

结果:

[[-2.26454173e+00  5.05703903e-01]
 [-2.08642550e+00 -6.55404729e-01]
 [-2.36795045e+00 -3.18477311e-01]
 [-2.30419716e+00 -5.75367713e-01]
 [-2.38877749e+00  6.74767397e-01]
  .....
 [ 2.04330844e+00  8.64684880e-01]
 [ 2.00169097e+00  1.04855005e+00]
 [ 1.87052207e+00  3.82821838e-01]
 [ 1.55849189e+00 -9.05313601e-01]
 [ 1.52084506e+00  2.66794575e-01]
 [ 1.37639119e+00  1.01636193e+00]
 [ 9.59298576e-01 -2.22839447e-02]]
（150，2）

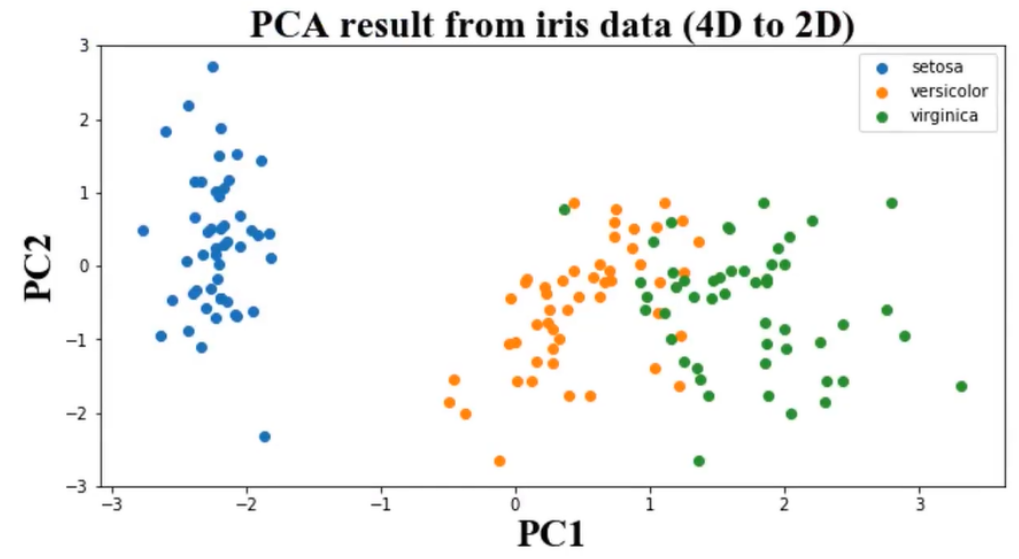
11、可视化降维后的数据

# 可视化展示pca结果
fig3 = plt.figure(figsize=(20, 10))
setosa = plt.scatter(X_pca[:, 0][y == 0], X_pca[:,1][y == 0])
versicolour = plt.scatter(X_pca[:, 0][y == 1], X_pca[:,1][y == 1])
virginica = plt.scatter(X_pca[:, 0][y == 2], X_pca[:,1][y == 2])
plt.legend((setosa, versicolour, virginica), ('setosa', 'versicolour', 'virginica'))
plt.show()

结果：

原来4维的话是无法可视化的，现在降为2维，从图中可以看到，蓝色是一种花，黄色是一种花，绿色是一种花，虽然黄色和绿色夹杂在一起，但是肉眼还是可以区分得开的。即通过PCA降维之后，这三种花实现了相关性最小。

至此第四步已经完成，现在来看第5步：基于降维后数据建立KNN模型，与原数据的表现（准确率）进行对比

12、基于降维后数据建立KNN模型

#建立KNN模型
from sklearn.neighbors import KNeighborsClassifier
KNN = KNeighborsClassifier(n_neighbors=3)
KNN.fit(X_pca,y)
# 预测
y_predict = KNN.predict(X_pca)
# 计算准确率
accuracy = accuracy_score(y,y_predict)
print(accuracy)

结果：0.9466666666666667

原来是0.96，下降了一点，说明效果其实还挺不错的。

完整代码：

#加载数据
import torch
import pandas as pd
import numpy as np
from sklearn.metrics import accuracy_score
# from matplotlib import pyplot as plt
import matplotlib
matplotlib.use('TkAgg')
import matplotlib.pyplot as plt

data = pd.read_csv('./data/iris_data.csv')
print(data)
#定义X,y
X = data.drop(['target','label'],axis=1) # 去掉最后两列
y = data.loc[:,'label']
print(X.shape,y.shape)#打印X，y的维度

#建立KNN模型
from sklearn.neighbors import KNeighborsClassifier
KNN = KNeighborsClassifier(n_neighbors=3)
KNN.fit(X,y) # 训练
y_predict = KNN.predict(X)# 预测
accuracy = accuracy_score(y,y_predict)# 计算准确率
print(accuracy)
# 对数据进行标准化处理(均值为0，方差为1)
from sklearn.preprocessing import StandardScaler
X_norm = StandardScaler().fit_transform(X)
print(X_norm)
# 计算均值和方差
x1_mean = X.loc[:,"sepal length"].mean()
x1_sigma = X.loc[:,"sepal length"].std()
x1_norm_mean = X_norm[:,0].mean()
x1_norm_sigma = X_norm[:,0].std()
print(x1_mean,x1_sigma,x1_norm_mean,x1_norm_sigma)

# 选取一个维度，可视化处理后的效果
fig1 = plt.figure(figsize=(20, 5))
# 原来的数据分布
plt.subplot(121)
plt.hist(X.loc[:,"sepal length"],bins=100)
# 标准化处理之后的数据
plt.subplot(122)
plt.hist(X_norm[:,0],bins=100)
plt.show()

# 进行与原数据等维度PCA，查看各主成分的方差比例
print(X.shape) # (150,4) 即元数据的维度为4
from sklearn.decomposition import PCA
pca = PCA(n_components=4) # 同等维度处理
# 等维度PCA后的数据x_pca
x_pca = pca.fit_transform(X_norm) # 参数为标准化处理之后的数据X_norm
print(x_pca)

# 计算每个主成分的方差比例
var_ratio = pca.explained_variance_ratio_
print(var_ratio) # [0.72770452 0.23030523 0.03683832 0.00515193]
# 可视化方差比例
fig2 = plt.figure(figsize=(20,5))
plt.bar([1, 2, 3, 4],var_ratio)
plt.xticks([1, 2, 3, 4],['PC1', 'PC2', 'PC3', 'PC4'])
plt.ylabel("variance ratio of each principle components")
plt.show()

pca = PCA(n_components=2) # 只需要保留前面两个成分 即开始降维
X_pca = pca.fit_transform(X_norm) # 降维后的数据
print(X_pca)
print(X_pca.shape)
# 可视化展示pca结果
fig3 = plt.figure(figsize=(20, 10))
setosa = plt.scatter(X_pca[:, 0][y == 0], X_pca[:,1][y == 0])
versicolour = plt.scatter(X_pca[:, 0][y == 1], X_pca[:,1][y == 1])
virginica = plt.scatter(X_pca[:, 0][y == 2], X_pca[:,1][y == 2])
plt.legend((setosa, versicolour, virginica), ('setosa', 'versicolour', 'virginica'))
plt.show()

# 基于降维后数据建立KNN模型，与原数据表现进行对比
#建立KNN模型
from sklearn.neighbors import KNeighborsClassifier
KNN = KNeighborsClassifier(n_neighbors=3)
KNN.fit(X_pca,y)
# 预测
y_predict = KNN.predict(X_pca)
# 计算准确率
accuracy = accuracy_score(y,y_predict)
print(accuracy)

总结：

1、通过计算数据对应的主成分(principle components)，可在减少数据维度同时尽可能保留主要信息;

2、为确定合适的主成分维度，可先对数据进行与原数据相同维度的PCA处理，再根据根据各个成分的数据方差确认主成分维度，即比例大的保留下来;