一个 Python 深度学习框架，它将数据封装成张量（Tensor）来进行处理。PyTorch 中的张量就是元素为同一种数据类型的多维矩阵。在 PyTorch 中，张量以 "类" 的形式封装起来，对张量的一些运算、处理的方法被封装在类中。
一、PyTorch-CPU版本环境配置
为了更好的管理不同的Python项目，通常建议创建一个虚拟环境。可以隔离不同项目的依赖项，避免项目之间的冲突。
（1）创建一个虚拟python环境：
conda create -n DL_Pytorch
conda activate DL_Pytorch
（2）查看虚拟环境列表
conda info --envs
conda info -e
conda env list
（3）激活虚拟环境
source activate .... （conda旧版本：4.3及更早的版本）
conda activate .... （conda新版本：4.4及以后）
（4）Pytorch的安装
pip install torch==1.10.0 -i https://pypi.tuna.tsinghua.edu.cn/simple
（5）Pytorch环境的删除
conda remove -n DL_Pytorch --all
下面进行操作：
1、打开anaconda Prompt
通过开始菜单：点击“开始”按钮，找到并点击“所有程序”，在列表中找到并点击“Anaconda”文件夹，然后选择“Anaconda Prompt”。
打开后界面如下：
2、查看有哪些环境
conda env list
如下所示：
3、创建一个虚拟python环境（基于3.11.5创建pytorch）
conda create -n DL_Pytorch python=3.11.5
查看有哪些环境
4、激活
conda activate DL_Pytorch
激活后，进入DL_Pytorch环境
5、安装pytorch
pip install torch==1.10.0 -i https://pypi.tuna.tsinghua.edu.cn/simple
结果：
我们不指定pytorch的版本重新安装
pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple
查看是否安装成功
6、安装完退出
conda deactivate
输入python，这样就可以执行代码了
二、张量的创建
在PyTorch中，张量（Tensor）是一种多维数组，可以表示各种类型的数据。
torch.size()是一个方法，而torch.shape是tensor的一个属性
1、张量基本类型
ndim查看维度
⚫ 0维张量：标量(scalar)
>>> import torch >>> scalar=torch.tensor(7) >>> scalar.ndim 0 >>> scalar.size() torch.Size([]) >>>
0维张量就是标量，即固定数值。0维没有方括号[]
torch.Size([])表示一个空的张量，即一个标量（scalar），它没有维度和元素。标量是一个单独的数值，没有其他维度信息。在PyTorch中，空的张量通常用于表示一个常数或者一个单独的数值
⚫ 1维张量：向量(vector)
>>> vector=torch.tensor([7,7]) >>> vector.ndim 1 >>> vector.size() torch.Size([2]) >>> vector.shape torch.Size([2]) >>>
向量是一维张量,1维只有一个方括号[]
torch.Size([1])表示一个具有一个维度的张量，该维度的大小为1。这个张量可以被认为是一个包含了一个元素的向量。虽然它只有一个元素，但它仍然具有一个维度信息。
⚫ 2维张量：矩阵(matrix)
>>> matrix=torch.tensor([[7,8],[9,10]]) >>> matrix.ndim 2 >>> matrix.size() torch.Size([2, 2]) >>> matrix.shape torch.Size([2, 2]) >>>
2维有两个方括号[[]]
⚫多维张量
>>> TENSOR=torch.tensor([[[1,2,3],[3,6,9],[2,4,5]]]) >>> TENSOR.ndim 3 >>> TENSOR.size() torch.Size([1, 3, 3]) >>> TENSOR.shape torch.Size([1, 3, 3]) >>>
3维张量有三个方括号[[[]]]
1表示[[1,2,3],[3,6,9],[2,4,5]]，第1个3表示[1,2,3],[3,6,9],[2,4,5]，第二个3表示1,2,3或3,6,9或2,4,5
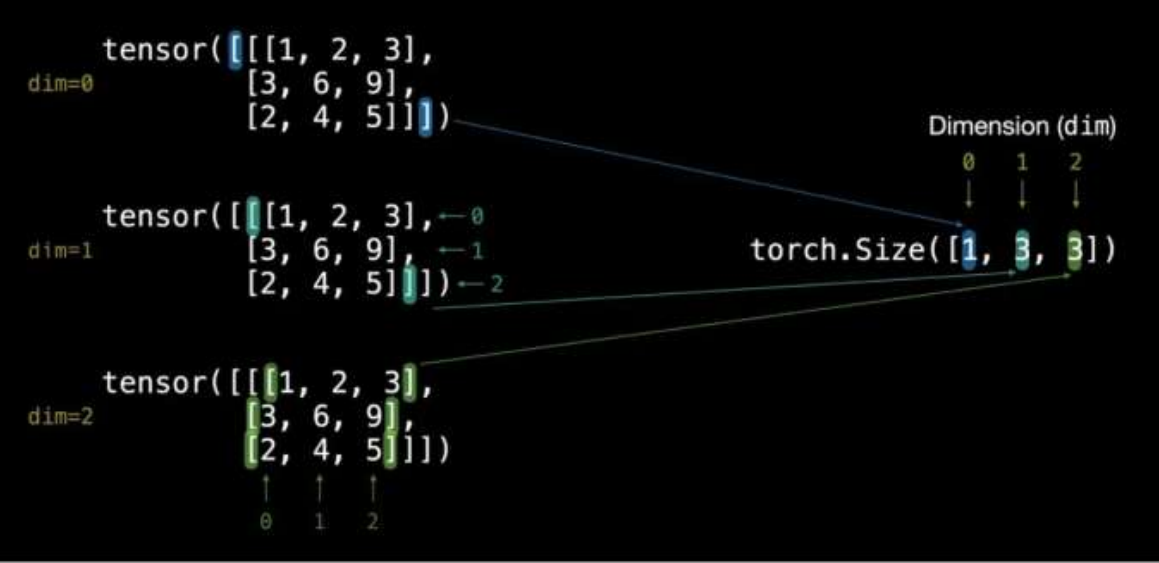
>>> data=torch.tensor([[[1,2,3,4],[3,6,9,7],[2,4,5,6]],[[1,2,3,6],[3,6,9,5],[2,4,5,7]]]) >>> data.ndim 3 >>> data.size() torch.Size([2, 3, 4]) >>> data.shape torch.Size([2, 3, 4]) >>>
`size()`返回张量的各个维度的大小
而通过指定索引，可以获取特定维度的大小。索引是从0开始的，所以`size(0)`是第一个维度，`size(1)`是第二个维度，以此类推。而`size(-1)`是Python中的负索引，表示最后一个维度，这在处理不定长度张量时特别有用，比如在自然语言处理中，序列长度可能变化，这时候用`size(-1)`可以方便地获取序列长度，而不需要知道总共有多少个维度。
import torch # 创建一个形状为 (2, 3, 4) 的三维张量 x = torch.randn(2, 3, 4) # 形状：batch=2, 序列长度=3, 特征维度=4 print(x.size(0)) # 输出第一个维度的大小：2 print(x.size(1)) # 输出第二个维度的大小：3 print(x.size(2)) # 输出第三个维度的大小：4
# 继续使用上述张量 x
print(x.size(-1)) # 输出最后一个维度的大小：4（等价于 x.size(2)）
print(x.size(-2)) # 输出倒数第二个维度的大小：3（等价于 x.size(1)）
print(x.size(-3)) # 输出倒数第三个维度的大小：2（等价于 x.size(0)）
2、张量基本创建方式
⚫ torch.tensor 根据指定数据创建张量
⚫ torch.Tensor 根据形状创建张量, 其也可用来创建指定数据的张量
⚫ torch.IntTensor、torch.FloatTensor、torch.DoubleTensor 创建指定类型的张量
1、torch.tensor() ：小写tensor表示根据指定数据创建张量(小写tensor只能接收数据)
import torch # 需要安装torch模块,虚拟环境中已经安装好了 import numpy as np # 1. 创建张量标量 data = torch.tensor(10) print(data) # 2. numpy 数组, 由于 data 为 float64, 下面代码也使用该类型 data = np.random.randn(2, 3)
print(data) data = torch.tensor(data) print(data) # 3. 直接传入2行3列的二维列表,加.表示float32, 下面代码使用默认元素类型 float32 data = [[10., 20., 30.], [40., 50., 60.]] data = torch.tensor(data) print(data)
numpy.random.randn(d1 , d2,…dn)
randn函数返回一个或一组样本，具有标准正太分布,dn表示每个维度,返回值为指定维度的array.
代码在pychartm中运行，但是要指定conda 环境
File→Setting→Project→Python Interpreter→Add Interpreter→
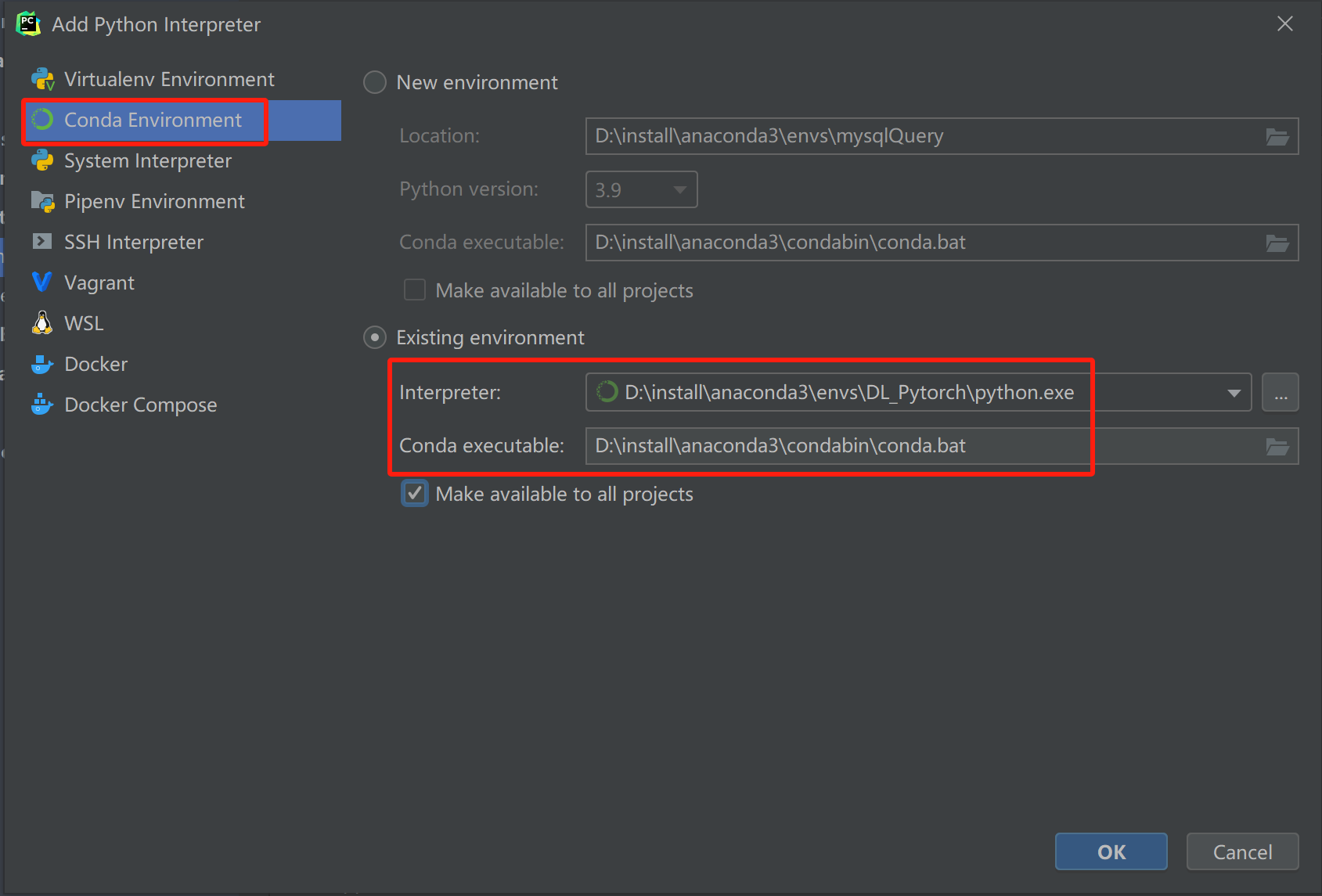
点击OK
运行结果如下：
tensor(10) [[-0.1013091 -0.6709214 0.37825196] [ 2.28405767 -0.12830494 0.14136493]] tensor([[-0.1013, -0.6709, 0.3783], [ 2.2841, -0.1283, 0.1414]], dtype=torch.float64) tensor([[10., 20., 30.], [40., 50., 60.]])
2.torch.Tensor() ：大写Tensor表示根据指定形状创建张量，也可以用来创建指定数据的张量（大写的Tensor可以指定形状也能指定数据）
import torch # 1. 创建2行3列的张量, 默认 dtype 为 float32 data = torch.Tensor(2, 3) print(data) # 2. 注意: 如果传递列表, 则创建包含指定元素的张量 data = torch.Tensor([10]) print(data) data = torch.Tensor([10, 20]) print(data)
结果：
tensor([[-2.1836e-11, 1.7768e-42, 0.0000e+00], [ 0.0000e+00, 0.0000e+00, 0.0000e+00]]) tensor([10.]) tensor([10., 20.])
3、torch.IntTensor()、torch.FloatTensor()、torch.DoubleTensor() 创建指定类型的张量（指定形状或数据的同事还指定类型）
Int表示int32，Short表示int16，Long表示int64，Float表示float32，Double表示float64
import torch # 1. 创建2行3列, dtype 为 int32 的张量 data = torch.IntTensor(2, 3) print(data) # 2. 注意: 如果传递的元素类型不正确, 则会进行类型转换,这里将小数点直接去掉，注意不是四舍五入 data = torch.IntTensor([2.5, 3.3]) print(data) # 3. 其他的类型 data = torch.ShortTensor(2,3) # int16 print(data) data = torch.LongTensor(2,3) # int64 print(data) data = torch.FloatTensor(2,3) # float32 print(data) data = torch.DoubleTensor(2,3) # float64 print(data)
结果：
tensor([[1770000736, 992, 0], [ 0, 0, 0]], dtype=torch.int32) tensor([2, 3], dtype=torch.int32) tensor([[0, 0, 0], [0, 0, 0]], dtype=torch.int16) tensor([[4262377685104, 0, 0], [ 0, 0, 0]]) tensor([[0., 0., 0.], [0., 0., 0.]]) tensor([[0., 0., 0.], [0., 0., 0.]], dtype=torch.float64)
3、创建线性和随机张量
⚫ torch.arange 和 torch.linspace 创建线性张量
⚫ torch.random.init_seed 和 torch.random.manual_seed 随机种子设置
⚫ torch.randn 创建随机张量
1、torch.arange()、torch.linspace() 创建线性张量
import torch # 1. 在指定区间按照步长生成元素 [start, end, step) data = torch.arange(0, 10, 2) print(data) # 2. 在指定区间按照元素个数生成 [start, end, steps] data = torch.linspace(0, 11, 10) print(data)
结果：
tensor([0, 2, 4, 6, 8]) tensor([ 0.0000, 1.2222, 2.4444, 3.6667, 4.8889, 6.1111, 7.3333, 8.5556, 9.7778, 11.0000])
2、torch.random.initial_seed()、torch.random.manual_seed() 随机数种子设置，torch.randn() 创建随机张量
import torch # 1. 创建随机张量 data = torch.randn(2, 3) # 创建2行3列张量 print(data) # 查看随机数种子 print('随机数种子:', torch.random.initial_seed()) # 2. 随机数种子设置 torch.random.manual_seed(100) data = torch.randn(2, 3) print(data) print('随机数种子:', torch.random.initial_seed())
结果：
tensor([[ 0.7593, 0.8782, -1.2609], [-2.2789, 0.2085, -1.5829]]) 随机数种子: 3696372704700 tensor([[ 0.3607, -0.2859, -0.3938], [ 0.2429, -1.3833, -2.3134]]) 随机数种子: 100
4、创建0-1张量
⚫ torch.ones 和 torch.ones_like 创建全1张量
⚫ torch.zeros 和 torch.zeros_like 创建全0张量
⚫ torch.full 和 torch.full_like 创建全为指定值张量
1、torch.ones()、torch.ones_like() 创建全1张量
import torch # 1. 创建指定形状全1张量 data = torch.ones(2, 3) print(data) # 2. 根据张量形状创建全1张量 data = torch.ones_like(data) print(data)
结果：
tensor([[1., 1., 1.], [1., 1., 1.]]) tensor([[1., 1., 1.], [1., 1., 1.]])
2、torch.zeros()、torch.zeros_like() 创建全0张量
import torch # 1. 创建指定形状全0张量 data = torch.zeros(2, 3) print(data) # 2. 根据张量形状创建全0张量 data = torch.zeros_like(data) print(data)
结果：
tensor([[0., 0., 0.], [0., 0., 0.]]) tensor([[0., 0., 0.], [0., 0., 0.]])
3、torch.full()、torch.full_like() 创建全为指定值张量
import torch # 1. 创建指定形状指定值的张量 data = torch.full([2, 3], 10) print(data) # 2. 根据张量形状创建指定值的张量 data = torch.full_like(data, 20) print(data) print(data.shape) print(data.size())
结果：
tensor([[10, 10, 10], [10, 10, 10]]) tensor([[20, 20, 20], [20, 20, 20]]) torch.Size([2, 3]) torch.Size([2, 3])
5、张量的类型转换
⚫ data.type(torch.DoubleTensor)
⚫ data.double()
1、data.type(torch.DoubleTensor)
import torch data = torch.full([2, 3], 10) print(data) print(data.dtype) # 将 data 元素类型转换为 float64 类型 data = data.type(torch.DoubleTensor) print(data) print(data.dtype)
结果:
tensor([[10, 10, 10], [10, 10, 10]]) torch.int64 tensor([[10., 10., 10.], [10., 10., 10.]], dtype=torch.float64) torch.float64
转换为其他类型
data = data.type(torch.ShortTensor) data = data.type(torch.IntTensor) data = data.type(torch.LongTensor) data = data.type(torch.FloatTensor)
2、data.double()
import torch data = torch.full([2, 3], 10) print(data.dtype) # 将 data 元素类型转换为 float64 类型 data = data.double() print(data.dtype)
结果：
torch.int64
torch.float64
转换为其他类型
data = data.short() data = data.int() data = data.long() data = data.float()
6、张量与NumPy数组互转
张量转换为NumPy数组
⚫ 使用 Tensor.numpy 函数可以将张量转换为 ndarray 数组，但是共享内存，可以使用 copy 函数避免共享。
import torch # 1. 将张量转换为 numpy 数组 data_tensor = torch.tensor([2, 3, 4]) print(type(data_tensor)) # 使用张量对象中的 numpy 函数进行转换 data_numpy = data_tensor.numpy() print(type(data_numpy)) # 注意: data_tensor 和 data_numpy 共享内存 # 修改其中的一个，另外一个也会发生改变 # data_tensor[0] = 100 data_numpy[0] = 100 print(data_tensor) print(data_numpy)
结果：
tensor([2, 3, 4]) <class 'torch.Tensor'> <class 'numpy.ndarray'> tensor([100, 3, 4]) [100 3 4]
使用Tensor.numpy()函数可以将张量转换为ndarray数组，但是共享内存，可以使用copy()函数避免共享
import torch # 2. 对象拷贝避免共享内存 data_tensor = torch.tensor([2, 3, 4]) # 使用张量对象中的 numpy 函数进行转换，通过copy方法拷贝对象 data_numpy = data_tensor.numpy().copy() print(type(data_tensor)) print(type(data_numpy)) # 注意: data_tensor 和 data_numpy 此时不共享内存 # 修改其中的一个，另外一个不会发生改变 # data_tensor[0] = 100 data_numpy[0] = 100 print(data_tensor) print(data_numpy)
结果：
<class 'torch.Tensor'> <class 'numpy.ndarray'> tensor([2, 3, 4]) [100 3 4]
NumPy数组转换为张量
⚫ 使用 from_numpy 可以将 ndarray 数组转换为 Tensor，默认共享内存，使用 copy 函数避免共享。
import torch import numpy as np data_numpy = np.array([2, 3, 4]) print(type(data_numpy)) # 将 numpy 数组转换为张量类型 # 1. from_numpy # 2. torch.tensor(ndarray) data_tensor = torch.from_numpy(data_numpy) print(type(data_tensor)) # nunpy 和 tensor 共享内存 # data_numpy[0] = 100 data_tensor[0] = 100 print(data_tensor) print(data_numpy)
结果：
<class 'numpy.ndarray'> <class 'torch.Tensor'> tensor([100, 3, 4], dtype=torch.int32) [100 3 4]
⚫ 使用 torch.tensor 可以将 ndarray 数组转换为 Tensor，默认不共享内存。
import numpy as np import torch data_numpy = np.array([2, 3, 4]) data_tensor = torch.tensor(data_numpy) # nunpy 和 tensor 不共享内存 # data_numpy[0] = 100 data_tensor[0] = 100 print(data_tensor) print(data_numpy)
结果：
tensor([100, 3, 4], dtype=torch.int32) [2 3 4]
7、标量张量和数字转换
⚫ 对于只有一个元素的张量，使用item()函数将该值从张量中提取出来
import torch # 当张量只包含一个元素时, 可以通过 item() 函数提取出该值 data = torch.tensor([20,]) print(data.item()) data = torch.tensor(30) print(data.item())
结果：
20 30
8、张量基本运算
加、减、乘、除、取负号：
add、sub、mul、div、neg
add_、sub_、mul_、div_、neg_（其中带下划线的版本会修改原数据）
加法：
import torch data = torch.randint(0, 10, [2, 3]) print(data) # 1. 不修改原数据 new_data = data.add(10) # 等价 new_data = data + 10 print(new_data) print(data) # 2. 直接修改原数据 注意: 带下划线的函数为修改原数据本身 new_data1 = data.add_(10) # 等价 data += 10 print(data) print(new_data1)
结果：
tensor([[9, 4, 6], [6, 2, 4]]) tensor([[19, 14, 16], [16, 12, 14]]) tensor([[9, 4, 6], [6, 2, 4]]) tensor([[19, 14, 16], [16, 12, 14]]) tensor([[19, 14, 16], [16, 12, 14]])
其他函数
print(data.sub(100)) print(data.mul(100)) print(data.div(100)) print(data.neg())
乘法：
import torch data = torch.randint(0, 10, [2, 3]) print(data) # 1. 不修改原数据 new_data = data.mul(10) # 等价 new_data = data + 10 print(new_data) print(data) # 2. 直接修改原数据 注意: 带下划线的函数为修改原数据本身 new_data1 = data.mul_(10) # 等价 data += 10 print(data) print(new_data1)
结果
tensor([[3, 2, 6], [2, 7, 7]]) tensor([[30, 20, 60], [20, 70, 70]]) tensor([[3, 2, 6], [2, 7, 7]]) tensor([[30, 20, 60], [20, 70, 70]]) tensor([[30, 20, 60], [20, 70, 70]])
全部运算
import torch data = torch.randint(0, 10, [2, 3]) print(data) # 1. 不修改原数据 new_data = data.add(10) # 等价 new_data = data + 10 print(new_data) print(data) # 2. 直接修改原数据 注意: 带下划线的函数为修改原数据本身 new_data1 = data.add_(10) # 等价 data += 10 print(data) print(new_data1) # 3. 其他函数 print(data.sub(100)) print(data.mul(100)) print(data.div(100)) print(data.neg())
结果:
tensor([[7, 8, 6], [3, 0, 0]]) tensor([[17, 18, 16], [13, 10, 10]]) tensor([[7, 8, 6], [3, 0, 0]]) tensor([[17, 18, 16], [13, 10, 10]]) tensor([[17, 18, 16], [13, 10, 10]]) tensor([[-83, -82, -84], [-87, -90, -90]]) tensor([[1700, 1800, 1600], [1300, 1000, 1000]]) tensor([[0.1700, 0.1800, 0.1600], [0.1300, 0.1000, 0.1000]]) tensor([[-17, -18, -16], [-13, -10, -10]])
9、点乘运算
点乘指（Hadamard）的是两个同维矩阵对应位置的元素相乘，使用mul 和运算符 * 实现。
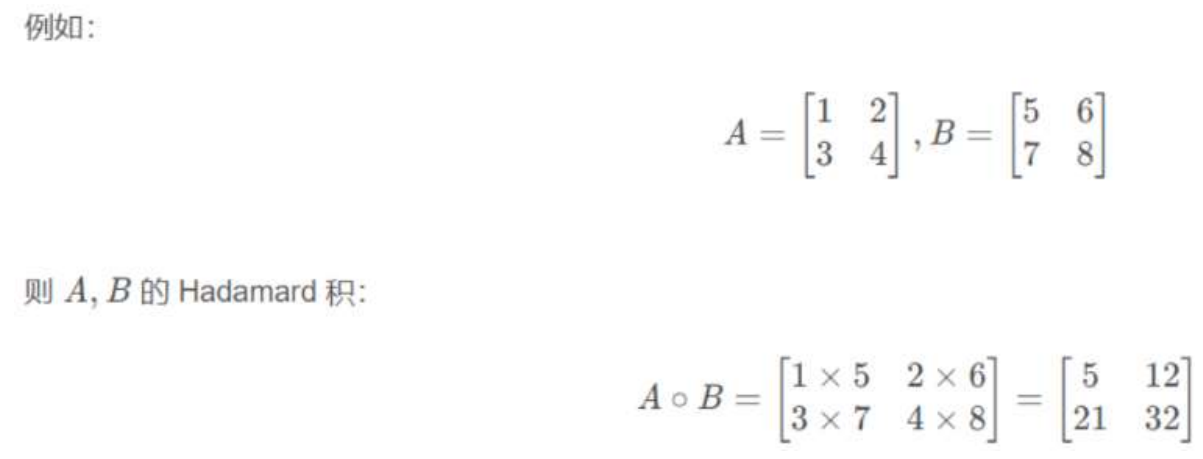
第一种方式：
import torch data1 = torch.tensor([[1, 2], [3, 4]]) data2 = torch.tensor([[5, 6], [7, 8]]) # 第一种方式 data = torch.mul(data1, data2) print(data)
结果：
tensor([[ 5, 12], [21, 32]])
第二种方式：
import torch data1 = torch.tensor([[1, 2], [3, 4]]) data2 = torch.tensor([[5, 6], [7, 8]]) # 第一种方式 # data = torch.mul(data1, data2) # print(data) # 第二种方式 data = data1 * data2 print(data)
结果：
tensor([[ 5, 12], [21, 32]])
10、矩阵乘法运算
矩阵乘法运算要求第一个矩阵 shape: (n, m)，第二个矩阵 shape: (m, p), 两个矩阵点积运算 shape 为: (n, p)。
1.运算符 @ 用于进行两个矩阵的乘积运算
2.torch.matmul 对进行乘积运算的两矩阵形状没有限定.对数输入的 shape 不同的张量, 对应的最后几个维度必须符合矩阵运算规则
方式一:
import torch # 点积运算 data1 = torch.tensor([[1, 2], [3, 4], [5, 6]]) print(data1.size()) # 3,2 data2 = torch.tensor([[5, 6], [7, 8]]) print(data2.size()) # 2,2 # 方式一: data3 = data1 @ data2 print("data3-->", data3) print(data3.size())
结果：
torch.Size([3, 2]) torch.Size([2, 2]) data3--> tensor([[19, 22], [43, 50], [67, 78]]) torch.Size([3, 2])
方式二：
import torch # 点积运算 data1 = torch.tensor([[1, 2], [3, 4], [5, 6]]) print(data1.size()) # 3,2 data2 = torch.tensor([[5, 6], [7, 8]]) print(data2.size()) # 2,2 # 方式一: # data3 = data1 @ data2 # print("data3-->", data3) # print(data3.size()) # 方式二: data4 = torch.matmul(data1, data2) print("data4-->", data4)
结果：
torch.Size([3, 2]) torch.Size([2, 2]) data4--> tensor([[19, 22], [43, 50], [67, 78]])
torch.mm
torch.mm是两个矩阵相乘，即两个二维的张量相乘
import torch mat1 = torch.randn(2,3) print("mat1=", mat1) mat2 = torch.randn(3,2) print("mat2=", mat2) mat3 = torch.mm(mat1, mat2) print("mat3=", mat3)
结果：
mat1= tensor([[ 1.5206, 1.0906, 0.4089], [-0.8510, -0.0643, -0.2519]]) mat2= tensor([[-0.4177, 0.4870], [ 0.3328, 1.2630], [ 0.7720, -0.2944]]) mat3= tensor([[ 0.0434, 1.9977], [ 0.1397, -0.4216]])
但是如果维度超过二维，则会报错。RuntimeError: self must be a matrix
torch.bmm
它其实就是加了一维batch，所以第一位为batch，并且要两个Tensor的batch相等。第二维和第三维就是mm运算了，同上了。
它的输入是三维张量，形状为 (batch_size, n, m) 和 (batch_size, m, p): 其中 n 是第一个矩阵的列数，m 是两个矩阵共享的维度，p 是第二个矩阵的列数。torch.bmm 将批中的每对矩阵相乘，返回一个新的三维张量，形状为 (batch_size, n, p)。
import torch mat1 = torch.randn(2, 2, 4) print("mat1=", mat1) mat2 = torch.randn(2, 4, 1) print("mat2=", mat2) mat3 = torch.bmm(mat1, mat2) print("mat3=", mat3, mat3.shape)
结果:
mat1= tensor([[[-0.6800, -1.6068, -3.0614, 0.7663], [ 0.8004, 0.2064, 0.8717, 0.8098]], [[ 1.0064, 0.2983, 0.0100, 0.8556], [-0.8972, -1.2213, -1.7379, 0.5852]]]) mat2= tensor([[[ 0.4274], [ 0.0815], [-0.4123], [-0.2875]], [[-0.3374], [ 1.1451], [ 1.2903], [ 0.9866]]]) mat3= tensor([[[ 0.6203], [-0.2334]], [[ 0.8589], [-2.7608]]]) torch.Size([2, 2, 1])
11、张量的运算函数
PyTorch 为每个张量封装很多实用的计算函数：
⚫ 均值
⚫ 平方根
⚫ 求和
⚫ 指数计算
⚫ 对数计算等等
常见运算函数
import torch data = torch.randint(1, 10, [2, 3], dtype=torch.float64) print(data) # 1. 计算均值 # 注意: tensor 必须为 Float 或者 Double 类型 print(data.mean()) print(data.mean(dim=0)) # 按列计算均值 print(data.mean(dim=1)) # 按行计算均值 # 2. 计算总和 print(data.sum()) print(data.sum(dim=0)) # 按列计算总和 print(data.sum(dim=1)) # 按行计算总和 # 3. 计算平方 print(torch.pow(data,2)) # 4. 计算平方根 print(data.sqrt()) # 5. 指数计算, e^n 次方 print(data.exp()) # 6. 对数计算 print(data.log()) # 以 e 为底 log(6)=ln6 print(data.log2()) #log2(6)=ln6/ln2 print(data.log10()) #log10(6)=ln6/ln10
结果：
tensor([[6., 8., 1.], [3., 3., 6.]], dtype=torch.float64) tensor(4.5000, dtype=torch.float64) tensor([4.5000, 5.5000, 3.5000], dtype=torch.float64) tensor([5., 4.], dtype=torch.float64) tensor(27., dtype=torch.float64) tensor([ 9., 11., 7.], dtype=torch.float64) tensor([15., 12.], dtype=torch.float64) tensor([[36., 64., 1.], [ 9., 9., 36.]], dtype=torch.float64) tensor([[2.4495, 2.8284, 1.0000], [1.7321, 1.7321, 2.4495]], dtype=torch.float64) tensor([[4.0343e+02, 2.9810e+03, 2.7183e+00], [2.0086e+01, 2.0086e+01, 4.0343e+02]], dtype=torch.float64) tensor([[1.7918, 2.0794, 0.0000], [1.0986, 1.0986, 1.7918]], dtype=torch.float64) tensor([[2.5850, 3.0000, 0.0000], [1.5850, 1.5850, 2.5850]], dtype=torch.float64) tensor([[0.7782, 0.9031, 0.0000], [0.4771, 0.4771, 0.7782]], dtype=torch.float64)
12、张量索引操作
在操作张量时，经常要去获取某些元素进行处理或者修改操作，在这里需要了解torch中的索引操作。
简单行、列索引
import torch # 随机生成数据 data = torch.randint(0, 10, [4, 5]) print(data) print(data[0]) # 获取第一行 print(data[:, 0]) # 获取第一列
结果：
tensor([[6, 5, 3, 3, 4], [5, 6, 3, 0, 2], [8, 3, 7, 0, 4], [7, 3, 6, 3, 5]]) tensor([6, 5, 3, 3, 4]) tensor([6, 5, 8, 7])
列表索引
import torch # 随机生成数据 data = torch.randint(0, 10, [4, 5]) print(data) print(data[0]) # 获取第一行 print(data[:, 0]) # 获取第一列 # 返回 (0, 1)、(1, 2) 两个位置的元素 print(data[[0, 1], [1, 2]]) # 返回 0、1 行的 1、2 列共4个元素 print(data[[[0], [1]], [1, 2]])
结果:
tensor([[8, 4, 9, 6, 3], [3, 3, 7, 6, 7], [3, 8, 6, 1, 8], [1, 9, 9, 9, 1]]) tensor([8, 4, 9, 6, 3]) tensor([8, 3, 3, 1]) tensor([4, 7]) tensor([[4, 9], [3, 7]])
范围索引
import torch # 随机生成数据 data = torch.randint(0, 10, [4, 5]) print(data) # 前3行的前2列数据 print(data[:3, :2]) # 第2行到最后的前2列数据 print(data[2:, :2])
结果:
tensor([[9, 6, 2, 9, 1], [0, 9, 1, 3, 8], [0, 0, 0, 6, 9], [8, 4, 6, 2, 2]]) tensor([[9, 6], [0, 9], [0, 0]]) tensor([[0, 0], [8, 4]])
布尔索引
import torch # 随机生成数据 data = torch.randint(0, 10, [4, 5]) print(data) # 第三列大于5的行数据 print(data[data[:, 2] > 5]) # 第二行大于5的列数据 print(data[:, data[1] > 5])
结果:
tensor([[0, 2, 3, 5, 1], [4, 9, 9, 4, 9], [8, 4, 5, 9, 6], [3, 2, 5, 6, 4]]) tensor([[4, 9, 9, 4, 9]]) tensor([[2, 3, 1], [9, 9, 9], [4, 5, 6], [2, 5, 4]])
多维索引
import torch data = torch.randint(0, 10, [3, 4, 5]) print(data) # 获取0轴上的第一个数据 print(data[0, :, :]) # 获取1轴上的第一个数据 print(data[:, 0, :]) # 获取2轴上的第一个数据 print(data[:, :, 0])
结果:
tensor([[[8, 6, 5, 5, 4], [3, 9, 5, 0, 2], [3, 3, 1, 8, 3], [5, 2, 6, 9, 8]], [[6, 4, 9, 6, 1], [4, 2, 5, 3, 7], [0, 5, 5, 7, 6], [8, 1, 9, 5, 9]], [[8, 9, 2, 1, 8], [8, 4, 9, 7, 7], [4, 8, 1, 1, 5], [0, 4, 7, 3, 5]]]) tensor([[8, 6, 5, 5, 4], [3, 9, 5, 0, 2], [3, 3, 1, 8, 3], [5, 2, 6, 9, 8]]) tensor([[8, 6, 5, 5, 4], [6, 4, 9, 6, 1], [8, 9, 2, 1, 8]]) tensor([[8, 3, 3, 5], [6, 4, 0, 8], [8, 8, 4, 0]])
多维张量的负数索引
mask[:, :, -2:] = 0的意思是将mask张量的每一个batch中的每一个序列的最后两个位置的值设为0。
# 生成掩码（示例：掩盖后两个位置） mask = torch.ones(batch_size, seq_len_q, seq_len_k) # (2,10,10) # 第一个维度全部保留，第二个冒号表示第二个维度全部保留，第三个部分是-2:，这表示从倒数第二个元素到最后一个元素，也就是最后两个元素。 mask[:, :, -2:] = 0 # 将最后两列设为 0
13、张量形状操作
reshape()函数reshape 函数可以在保证张量数据不变的前提下改变数据的维度，将其转换成指定的形状。
import torch data = torch.tensor([[10, 20, 30], [40, 50, 60]]) # 1. 使用 shape 属性或者 size 方法都可以获得张量的形状 print(data.shape, data.shape[0], data.shape[1]) # 2,3 2, 3 print(data.size(), data.size(0), data.size(1)) # 2. 使用 reshape 函数修改张量形状 new_data = data.reshape(1, 6) print(new_data) print(new_data.shape) new_data1 = data.reshape(3, 2) print(new_data1) print(new_data1.shape)
结果:
torch.Size([2, 3]) 2 3 torch.Size([2, 3]) 2 3 tensor([[10, 20, 30, 40, 50, 60]]) torch.Size([1, 6]) tensor([[10, 20], [30, 40], [50, 60]]) torch.Size([3, 2])
squeeze()和unsqueeze()函数
squeeze 函数删除形状为 1 的维度（降维），unsqueeze 函数添加形状为1的维度（升维）。
import torch mydata1 = torch.tensor([1, 2, 3, 4, 5]) print('mydata1--->', mydata1.shape, mydata1) # 一个普通的数组 1维数据 mydata2 = mydata1.unsqueeze(dim=0) # 在0维度上升维 print('在0维度上 拓展维度：', mydata2, mydata2.shape) #1*5 mydata3 = mydata1.unsqueeze(dim=1) # 在1维度上升维 print('在1维度上 拓展维度：', mydata3, mydata3.shape) #5*1 mydata4 = mydata1.unsqueeze(dim=-1) # 在-1维度上升维 print('在-1维度上 拓展维度：', mydata4, mydata4.shape) #5*1 mydata5 = mydata4.squeeze() print('压缩维度：', mydata5, mydata5.shape) #1*5
结果:
mydata1---> torch.Size([5]) tensor([1, 2, 3, 4, 5]) 在0维度上 拓展维度： tensor([[1, 2, 3, 4, 5]]) torch.Size([1, 5]) 在1维度上 拓展维度： tensor([[1], [2], [3], [4], [5]]) torch.Size([5, 1]) 在-1维度上 拓展维度： tensor([[1], [2], [3], [4], [5]]) torch.Size([5, 1]) 压缩维度： tensor([1, 2, 3, 4, 5]) torch.Size([5])
transpose()和permute()函数
transpose 函数可以实现交换张量形状的指定维度, 例如: 一个张量的形状为 (2, 3, 4) 可以通过 transpose 函数把 3 和 4进行交换, 将张量的形状变为 (2, 4, 3) 。 permute 函数可以一次交换更多的维度。
import torch import numpy as np data = torch.tensor(np.random.randint(0, 10, [3, 4, 5])) print('data shape:', data.size()) print(data) # 1 交换1和2维度 mydata2 = torch.transpose(data, 1, 2) print(mydata2) print('mydata2.shape--->', mydata2.shape)
结果:
data shape: torch.Size([3, 4, 5]) tensor([[[2, 2, 4, 3, 0], [9, 7, 2, 6, 4], [7, 7, 3, 0, 3], [1, 9, 1, 2, 2]], [[9, 5, 2, 1, 4], [7, 5, 5, 4, 6], [4, 7, 9, 9, 7], [7, 2, 9, 8, 9]], [[1, 7, 1, 0, 9], [6, 1, 6, 0, 8], [2, 0, 0, 1, 3], [9, 4, 3, 3, 0]]], dtype=torch.int32) tensor([[[2, 9, 7, 1], [2, 7, 7, 9], [4, 2, 3, 1], [3, 6, 0, 2], [0, 4, 3, 2]], [[9, 7, 4, 7], [5, 5, 7, 2], [2, 5, 9, 9], [1, 4, 9, 8], [4, 6, 7, 9]], [[1, 6, 2, 9], [7, 1, 0, 4], [1, 6, 0, 3], [0, 0, 1, 3], [9, 8, 3, 0]]], dtype=torch.int32) mydata2.shape---> torch.Size([3, 5, 4])
将data 的形状修改为 (4, 5, 3), 需要变换多次
import torch import numpy as np data = torch.tensor(np.random.randint(0, 10, [3, 4, 5])) print('data shape:', data.size()) print(data) # 2 将data 的形状修改为 (4, 5, 3), 需要变换多次 mydata3 = torch.transpose(data, 0, 1) # 交换0和1维度变为(4,3,5) print(mydata3) mydata4 = torch.transpose(mydata3, 1, 2) # 交换1和2维度变为(4,5,3) print(mydata4) print('mydata4.shape--->', mydata4.shape)
结果:
data shape: torch.Size([3, 4, 5]) tensor([[[5, 6, 8, 8, 0], [6, 0, 7, 7, 4], [6, 5, 9, 6, 1], [0, 5, 8, 9, 1]], [[8, 1, 0, 6, 8], [5, 9, 2, 6, 9], [7, 7, 4, 7, 5], [1, 1, 5, 4, 6]], [[2, 5, 2, 8, 0], [8, 8, 0, 6, 7], [0, 9, 1, 0, 6], [3, 5, 1, 9, 8]]], dtype=torch.int32) tensor([[[5, 6, 8, 8, 0], [8, 1, 0, 6, 8], [2, 5, 2, 8, 0]], [[6, 0, 7, 7, 4], [5, 9, 2, 6, 9], [8, 8, 0, 6, 7]], [[6, 5, 9, 6, 1], [7, 7, 4, 7, 5], [0, 9, 1, 0, 6]], [[0, 5, 8, 9, 1], [1, 1, 5, 4, 6], [3, 5, 1, 9, 8]]], dtype=torch.int32) tensor([[[5, 8, 2], [6, 1, 5], [8, 0, 2], [8, 6, 8], [0, 8, 0]], [[6, 5, 8], [0, 9, 8], [7, 2, 0], [7, 6, 6], [4, 9, 7]], [[6, 7, 0], [5, 7, 9], [9, 4, 1], [6, 7, 0], [1, 5, 6]], [[0, 1, 3], [5, 1, 5], [8, 5, 1], [9, 4, 9], [1, 6, 8]]], dtype=torch.int32) mydata4.shape---> torch.Size([4, 5, 3])
transpose是PyTorch中的方法，用于交换张量的两个维度。参数-2和-1是维度的索引，这里使用负数表示从后往前数的维度。例如，对于一个三维张量(batch_size, seq_len, d_model)，-1对应的是d_model，-2对应的是seq_len，-3对应的是batch_size。
K.transpose(-2, -1)的作用就是交换倒数第二和倒数第一的维度。假设K的形状是(batch_size, seq_len, d_k)，那么转置后的形状会变成(batch_size, d_k, seq_len)。
import torch # 假设 K 是一个三维张量，形状为 (batch_size, seq_len, d_k) K = torch.randn(2, 10, 64) # 形状 (2, 10, 64) # 转置最后两个维度 K_transposed = K.transpose(-2, -1) # 转置后的形状为 (2, 64, 10)
使用 permute 函数将形状修改为 (4, 5, 3)
方法一:
import torch import numpy as np data = torch.tensor(np.random.randint(0, 10, [3, 4, 5])) print('data shape:', data.size()) print(data) # 3 使用 permute 函数将形状修改为 (4, 5, 3) # 3-1 方法1 mydata5 = torch.permute(data, [1, 2, 0]) print('mydata5.shape--->', mydata5.shape) print(mydata5)
结果:
data shape: torch.Size([3, 4, 5]) tensor([[[1, 1, 4, 8, 9], [5, 2, 3, 1, 8], [6, 6, 8, 6, 5], [8, 9, 6, 4, 6]], [[1, 4, 2, 0, 1], [9, 8, 9, 7, 4], [9, 8, 5, 9, 8], [4, 8, 5, 7, 2]], [[7, 2, 3, 6, 7], [7, 3, 5, 7, 3], [6, 4, 6, 5, 5], [6, 5, 3, 1, 9]]], dtype=torch.int32) mydata5.shape---> torch.Size([4, 5, 3]) tensor([[[1, 1, 7], [1, 4, 2], [4, 2, 3], [8, 0, 6], [9, 1, 7]], [[5, 9, 7], [2, 8, 3], [3, 9, 5], [1, 7, 7], [8, 4, 3]], [[6, 9, 6], [6, 8, 4], [8, 5, 6], [6, 9, 5], [5, 8, 5]], [[8, 4, 6], [9, 8, 5], [6, 5, 3], [4, 7, 1], [6, 2, 9]]], dtype=torch.int32)
方法二:
import torch import numpy as np data = torch.tensor(np.random.randint(0, 10, [3, 4, 5])) print('data shape:', data.size()) print(data) # 3 使用 permute 函数将形状修改为 (4, 5, 3) # 3-2 方法2 mydata6 = data.permute([1, 2, 0]) print('mydata6.shape--->', mydata6.shape) print(mydata6)
结果:
data shape: torch.Size([3, 4, 5]) tensor([[[9, 8, 9, 8, 4], [9, 5, 0, 5, 7], [1, 1, 7, 8, 3], [3, 7, 0, 1, 4]], [[6, 6, 6, 3, 3], [9, 7, 3, 0, 2], [7, 6, 8, 4, 9], [3, 7, 1, 9, 2]], [[7, 7, 9, 5, 1], [4, 3, 2, 6, 7], [1, 1, 3, 7, 3], [6, 9, 8, 0, 0]]], dtype=torch.int32) mydata6.shape---> torch.Size([4, 5, 3]) tensor([[[9, 6, 7], [8, 6, 7], [9, 6, 9], [8, 3, 5], [4, 3, 1]], [[9, 9, 4], [5, 7, 3], [0, 3, 2], [5, 0, 6], [7, 2, 7]], [[1, 7, 1], [1, 6, 1], [7, 8, 3], [8, 4, 7], [3, 9, 3]], [[3, 3, 6], [7, 7, 9], [0, 1, 8], [1, 9, 0], [4, 2, 0]]], dtype=torch.int32)
view()和contiguous()函数
view 函数也可以用于修改张量的形状，只能用于存储在整块内存中的张量。在 PyTorch 中，有些张量是由不同的数据块组成的，它们并没有存储在整块的内存中，view 函数无法对这样的张量进行变形处理，例如: 一个张量经过了transpose 或者 permute 函数的处理之后，就无法使用 view 函数进行形状操作。
import torch # 1 一个张量经过了 transpose 或者 permute 函数的处理之后，就无法使用view 函数进行形状操作 # 若要使用view函数, 需要使用contiguous() 变成连续以后再使用view函数 # 2 判断张量是否使用整块内存 data = torch.tensor( [[10, 20, 30],[40, 50, 60]]) print('data--->', data, data.shape) # 1 判断是否使用整块内存 print(data.is_contiguous()) # True # 2 view mydata2 = data.view(3, 2) print('mydata2--->', mydata2, mydata2.shape) # 3 判断是否使用整块 print('mydata2.is_contiguous()--->', mydata2.is_contiguous()) # True
结果:
data---> tensor([[10, 20, 30], [40, 50, 60]]) torch.Size([2, 3]) True mydata2---> tensor([[10, 20], [30, 40], [50, 60]]) torch.Size([3, 2]) mydata2.is_contiguous()---> True
使用 transpose 函数修改形状
import torch # 1 一个张量经过了 transpose 或者 permute 函数的处理之后，就无法使用view 函数进行形状操作 # 若要使用view函数, 需要使用contiguous() 变成连续以后再使用view函数 # 2 判断张量是否使用整块内存 data = torch.tensor( [[10, 20, 30],[40, 50, 60]]) print('data--->', data, data.shape) # 4 使用 transpose 函数修改形状 mydata3 = torch.transpose(data, 0, 1) print('mydata3--->', mydata3, mydata3.shape) print('mydata3.is_contiguous()--->', mydata3.is_contiguous()) # False # 5 需要先使用 contiguous 函数转换为整块内存的张量，再使用 view 函数 print (mydata3.contiguous().is_contiguous()) # True mydata4 = mydata3.contiguous().view(2, 3) print('mydata4--->', mydata4.shape, mydata4)
结果:
data---> tensor([[10, 20, 30], [40, 50, 60]]) torch.Size([2, 3]) mydata3---> tensor([[10, 40], [20, 50], [30, 60]]) torch.Size([3, 2]) mydata3.is_contiguous()---> False True mydata4---> torch.Size([2, 3]) tensor([[10, 40, 20], [50, 30, 60]])
14、张量拼接操作
torch.cat()函数可以将两个张量根据指定的维度拼接起来，不改变维度数。
import torch data1 = torch.randint(0, 10, [1, 2, 3]) data2 = torch.randint(0, 10, [1, 2, 3]) print(data1) print(data2) # 1. 按0维度拼接 new_data = torch.cat([data1, data2], dim=0) print(new_data) print(new_data.shape) # 2. 按1维度拼接 new_data = torch.cat([data1, data2], dim=1) print(new_data) print(new_data.shape) # 3. 按2维度拼接 new_data = torch.cat([data1, data2], dim=2) print(new_data) print(new_data.shape)
结果
tensor([[[5, 0, 3], [7, 1, 9]]]) tensor([[[5, 3, 0], [9, 7, 1]]]) tensor([[[5, 0, 3], [7, 1, 9]], [[5, 3, 0], [9, 7, 1]]]) torch.Size([2, 2, 3]) tensor([[[5, 0, 3], [7, 1, 9], [5, 3, 0], [9, 7, 1]]]) torch.Size([1, 4, 3]) tensor([[[5, 0, 3, 5, 3, 0], [7, 1, 9, 9, 7, 1]]]) torch.Size([1, 2, 6])
15、自动微分模块
pytorch的自动微分是一种自动计算导数和梯度的技术
手动计算梯度的代码
import numpy as np import matplotlib.pyplot as plt def f(x): # 计算二次函数f(x)=x^2+3*x+2的值 return x*x + 3*x + 2 def df(x): # 手动推导出改函数的导数 return 2*x + 3 if __name__ == '__main__': x = np.linspace(-6.5,3.5, 1000);# 使用linespace 生成自变量x的序列 y_f = f(x) # 计算函数值 y_df = df(x) # 计算导函数值 # 绘制f和df的图像 plt.plot(x,y_f, label = 'f(x)=x*x + 3*x + 2') plt.plot(x, y_df, label='f(x)=2x + 3') plt.legend() plt.grid(True); plt.show()
结果：定义域的范围[-6.5,3.5]
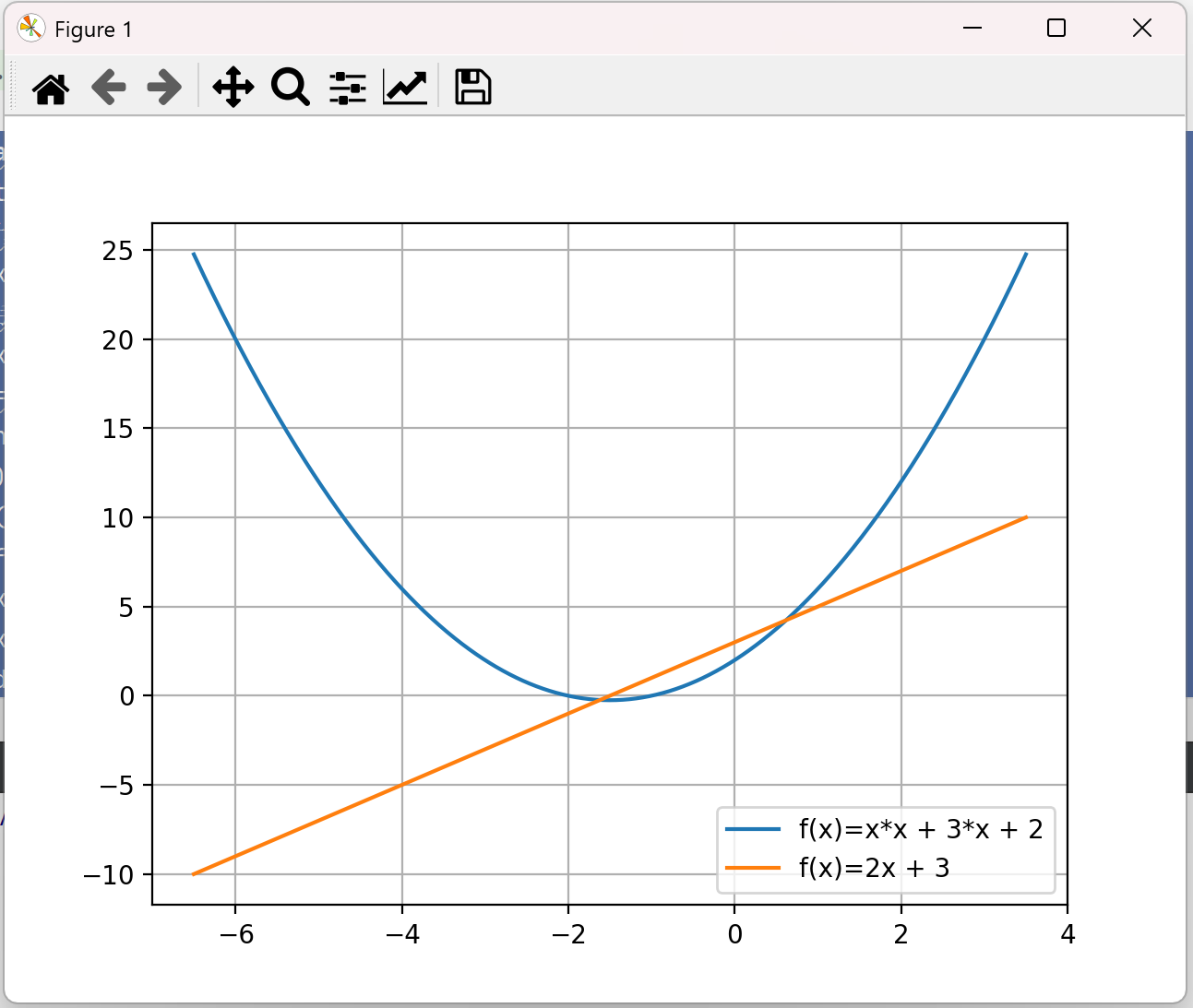
使用pytorch的自动微分功能，只需要定义原函数f(x)，不再需要定义导函数df(x)。我们可以通过backward函数自动计算梯度
import torch import matplotlib.pyplot as plt def f(x): # 计算二次函数f(x)=x^2+3*x+2的值 return x*x + 3*x + 2 if __name__ == '__main__': #生成自变量序列x，张量x，需要自动微分功能 x= torch.linspace(-6.5, 3.5, 1000, requires_grad=True) y_f = f(x) # 计算函数f的值 # 使用backward函数，计算f(x)关于x的梯度 # 这样，所有的梯度值，就都会保存在x.grad中 y_f.sum().backward() # 因为backward()函数只能对标量进行操作 #需要先使用y_f.sum，将y_f中的元素求和，将其转换为一个标量 #再在这个标量上调用backward，计算梯度 # 将梯度值x.grad、函数值y_f、自变量x，从pytorch张量转换为numpy数组 # 注意，转换前需要调用detach函数 y_df = x.grad.detach().numpy() y_f = y_f.detach().numpy() x = x.detach().numpy() # detach方法会创建一个原张量的副本，该副本不会跟踪张量的梯度 # 使用detach后，才能正常的将张量转换为numpy数组 # 而不影响自动梯度的计算 # 绘制f和df的图像 plt.plot(x,y_f, label = 'f(x)=x*x + 3*x + 2') plt.plot(x, y_df, label='f(x)=2x + 3') plt.legend() plt.grid(True); plt.show()
结果：
使用backward函数，计算f(x)关于x的梯度，所有的梯度值，就都会保存在x.grad中
grad.zero_方法用于将张量中的梯度清零，是梯度下降过程中必须要调用的方法
def f(x):# 定义原函数f return x*x-4*x-5 def df(x):# 定义导函数df，导函数用于验证程序的结果 return 2*x-4 import torch #初始化一个带有梯度的张量 x=torch.tensor([0.0],requires_grad=True) y=f(x) # 计算函数值y y.backward() # 调用backward计算y关于x的梯度 print("第1次打印:") print("x的值:",x.data)#打印X print("x的梯度值:",x.grad.data)#打印x.grad print("验证，x的梯度值:",df(x).data)#打印函数df验证梯度值 print("") x.grad.zero_() # 将梯度清零 y=f(x) y.backward() print("第2次打印:") print("x的值:",x.data)#打印X print("x的梯度值:",x.grad.data)#打印x.grad print("验证，x的梯度值:",df(x).data)#打印函数df验证梯度值 print("") # 第三次计算y和梯度前，不再使用grad.zero_ y=f(x) y.backward() print("第3次打印:") print("x的值:",x.data)#打印X print("x的梯度值:",x.grad.data)#打印x.grad print("验证，x的梯度值:",df(x).data)#打印函数df验证梯度值 print("")
结果：
第1次打印: x的值: tensor([0.]) x的梯度值: tensor([-4.]) 验证，x的梯度值: tensor([-4.]) 第2次打印: x的值: tensor([0.]) x的梯度值: tensor([-4.]) 验证，x的梯度值: tensor([-4.]) 第3次打印: x的值: tensor([0.]) x的梯度值: tensor([-8.]) 验证，x的梯度值: tensor([-4.])
第一次计算之后，使用了grad.zero_对梯度进行了清零，故第二次计算梯度为-4是正确的，第三次计算之前没有使用grad.zero_对梯度进行清零，在调用backward时，梯度都会累加到已有的梯度上，也就是-4+(-4)=-8
使用自动微分，实现梯度下降
下面我们使用pytorch的自动微分，实现函数f(x,y)=x2 +y2 ，当x=0,y=0，函数取得极小值0
def f(x,y): return x**2+y**2 import torch # 随意设置初始值 x=torch.tensor([1.1],requires_grad=True) y=torch.tensor([2.1],requires_grad=True) n=100 # 迭代轮数 alpha =0.05 #迭代速率，alpha用于控制“一小步”的大小 for i in range(1,n+1):# 进入梯度下降算法的循环 z =f(x,y)#计算函数值 z.backward()#调用backward，计算z关于x和y的梯度 #使用backward方法后，梯度会累加到对应张量的grad属性中 # 计算的梯度值会保存到x.grad和y.grad中 # 更新x.data和y.data x.data -= alpha * x.grad.data y.data -= alpha * y.grad.data print("x的梯度值%s y的梯度值%s" % (x.grad.data, y.grad.data)) # 如果后续要重复调用backward，为下一次迭代做准备 x.grad.zero_() #将张量中的梯度清零 y.grad.zero_() #将张量中的梯度清零 print(f'After {i} iterations,'# 迭代轮数i f'x= {x.item():.3f}，'# 自变量X f'y = {y.item():.3f}，'# 自变量y f'f(x，y)= {z.item():.3f}，' )# 函数值f(x,y)
结果：
x的梯度值tensor([2.2000]) y的梯度值tensor([4.2000]) After 1 iterations,x= 0.990，y = 1.890，f(x，y)= 5.620， x的梯度值tensor([1.9800]) y的梯度值tensor([3.7800]) After 2 iterations,x= 0.891，y = 1.701，f(x，y)= 4.552， x的梯度值tensor([1.7820]) y的梯度值tensor([3.4020]) After 3 iterations,x= 0.802，y = 1.531，f(x，y)= 3.687， x的梯度值tensor([1.6038]) y的梯度值tensor([3.0618]) After 4 iterations,x= 0.722，y = 1.378，f(x，y)= 2.987， x的梯度值tensor([1.4434]) y的梯度值tensor([2.7556]) After 5 iterations,x= 0.650，y = 1.240，f(x，y)= 2.419， x的梯度值tensor([1.2991]) y的梯度值tensor([2.4801]) After 6 iterations,x= 0.585，y = 1.116，f(x，y)= 1.960， x的梯度值tensor([1.1692]) y的梯度值tensor([2.2321]) After 7 iterations,x= 0.526，y = 1.004，f(x，y)= 1.587， ....... After 95 iterations,x= 0.000，y = 0.000，f(x，y)= 0.000， x的梯度值tensor([9.8960e-05]) y的梯度值tensor([0.0002]) After 96 iterations,x= 0.000，y = 0.000，f(x，y)= 0.000， x的梯度值tensor([8.9064e-05]) y的梯度值tensor([0.0002]) After 97 iterations,x= 0.000，y = 0.000，f(x，y)= 0.000， x的梯度值tensor([8.0158e-05]) y的梯度值tensor([0.0002]) After 98 iterations,x= 0.000，y = 0.000，f(x，y)= 0.000， x的梯度值tensor([7.2142e-05]) y的梯度值tensor([0.0001]) After 99 iterations,x= 0.000，y = 0.000，f(x，y)= 0.000， x的梯度值tensor([6.4928e-05]) y的梯度值tensor([0.0001]) After 100 iterations,x= 0.000，y = 0.000，f(x，y)= 0.000，
训练神经网络时，最常用的算法就是反向传播。在该算法中，参数（模型权重）会根据损失函数关于对应参数的梯度进行调整。为了计算这些梯度，PyTorch内置了名为 torch.autograd 的微分引擎。它支持任意计算图的自动梯度计算：
接下来我们使用这个结构进行自动微分模块的介绍。我们使用 backward 方法、grad 属性来实现梯度的计算和访问.
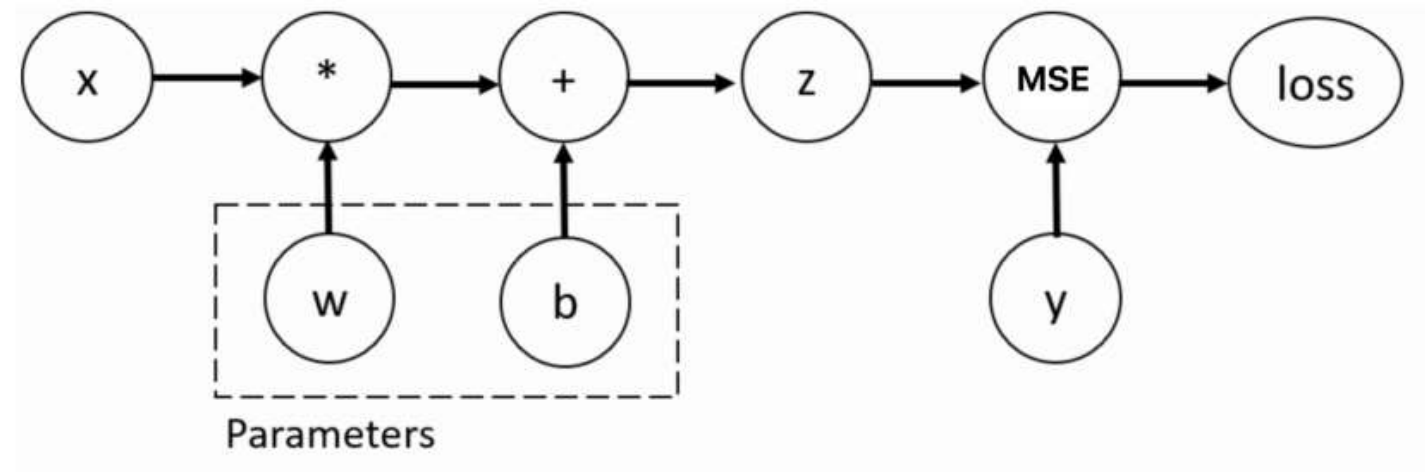
import torch # 1. 当X为标量时梯度的计算 def test01(): x = torch.tensor(5) # 目标值 y = torch.tensor(0.) # 设置要更新的权重和偏置的初始值 w = torch.tensor(1., requires_grad=True, dtype=torch.float32) b = torch.tensor(3., requires_grad=True, dtype=torch.float32) # 设置网络的输出值 z = x * w + b # 矩阵乘法 # 设置损失函数，并进行损失的计算 loss = torch.nn.MSELoss() loss = loss(z, y) # 自动微分 loss.backward() # 打印 w,b 变量的梯度 # backward 函数计算的梯度值会存储在张量的 grad 变量中 print("W的梯度:", w.grad) print("b的梯度", b.grad) test01()
结果:
W的梯度: tensor(80.) b的梯度 tensor(16.)
当X为矩阵时梯度的计算
import torch def test02(): # 输入张量 2*5 x = torch.ones(2,5) print(x) # 目标值是 2*3 y = torch.zeros(2,3) # 设置要更新的权重和偏置的初始值 w = torch.randn(5, 3,requires_grad=True) b = torch.randn(3, requires_grad=True) # 设置网络的输出值 z = torch.matmul(x, w) + b # 矩阵乘法 # 设置损失函数，并进行损失的计算 loss = torch.nn.MSELoss() loss = loss(z, y) # 自动微分 loss.backward() # 打印 w,b 变量的梯度 # backward 函数计算的梯度值会存储在张量的 grad 变量中 print("W的梯度:", w.grad) print("b的梯度", b.grad) test02()
结果:
tensor([[1., 1., 1., 1., 1.], [1., 1., 1., 1., 1.]]) W的梯度: tensor([[ 1.8749, -1.6302, 0.7990], [ 1.8749, -1.6302, 0.7990], [ 1.8749, -1.6302, 0.7990], [ 1.8749, -1.6302, 0.7990], [ 1.8749, -1.6302, 0.7990]]) b的梯度 tensor([ 1.8749, -1.6302, 0.7990])
本小节主要讲解了 PyTorch 中非常重要的自动微分模块的使用和理解。我们对需要计算梯度的张量需要设置 requires_grad=True 属性。
15、线性回归案例
掌握PyTorch构建线性回归模型相关API
我们使用 PyTorch 的各个组件来构建线性回归的实现。在pytorch中进行模型构建的整个流程一般分为四个步骤：
⚫ 准备训练集数据
⚫ 构建要使用的模型
⚫ 设置损失函数和优化器
⚫ 模型训练
要使用的API
⚫ 使用 PyTorch 的 nn.MSELoss() 代替自定义的平方损失函数
⚫ 使用 PyTorch 的 data.DataLoader 代替自定义的数据加载器
⚫ 使用 PyTorch 的 optim.SGD 代替自定义的优化器
⚫ 使用 PyTorch 的 nn.Linear 代替自定义的假设函数
代码如下:
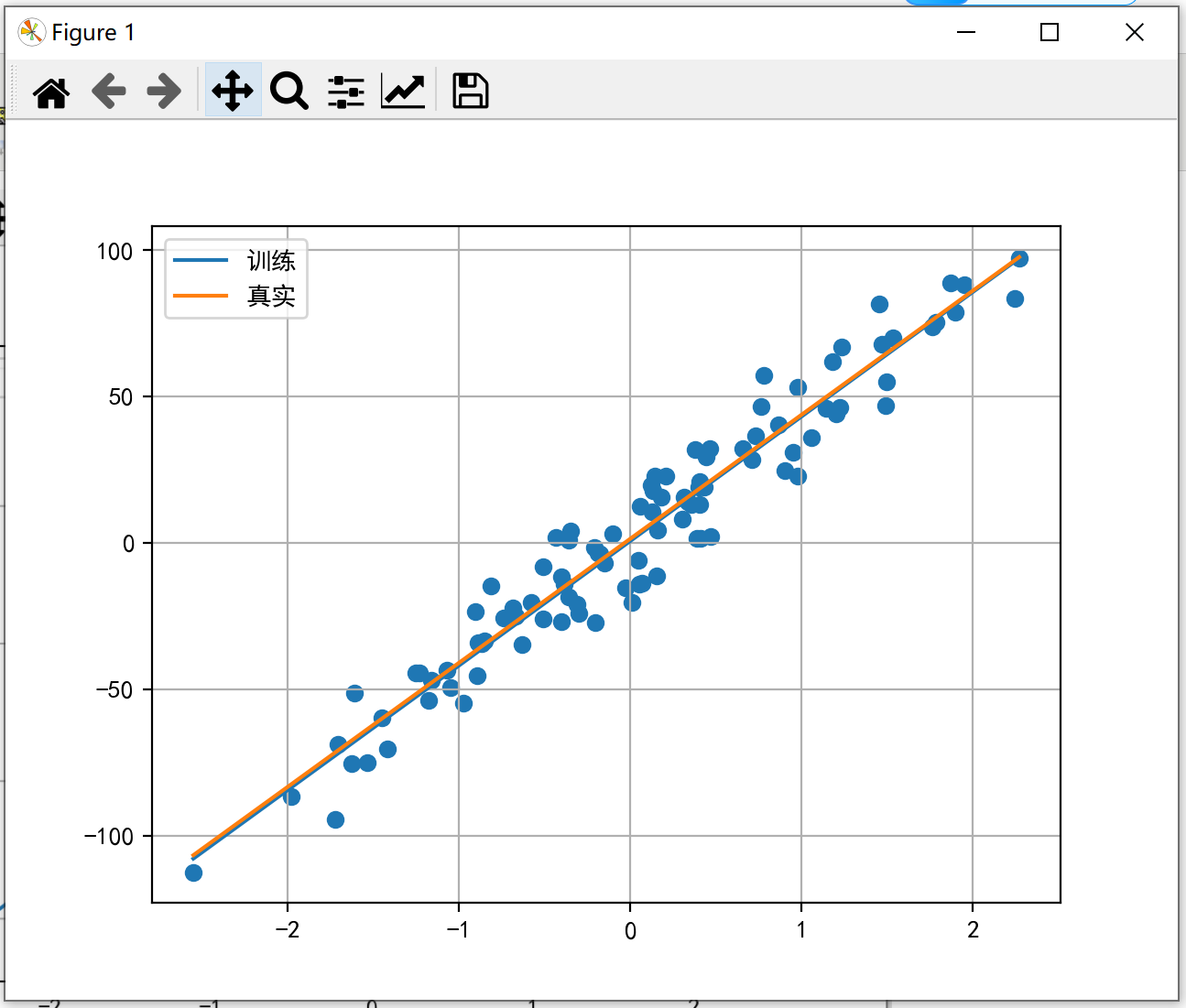
# 导入相关模块 import torch from torch.utils.data import TensorDataset # 构造数据集对象 from torch.utils.data import DataLoader # 数据加载器 from torch import nn # nn模块中有平方损失函数和假设函数 from torch import optim # optim模块中有优化器函数 from sklearn.datasets import make_regression # 创建线性回归模型数据集 import matplotlib.pyplot as plt plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签 plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号 # 数据集构建 def create_dataset(): x, y, coef = make_regression(n_samples=100, n_features=1, noise=10, coef=True, bias=1.5, random_state=0) # 将构建数据转换为张量类型 x = torch.tensor(x) y = torch.tensor(y) return x, y, coef if __name__ == "__main__": # 生成的数据 x, y, coef = create_dataset() # 绘制数据的真实的线性回归结果 plt.scatter(x, y) x = torch.linspace(x.min(), x.max(), 1000) y1 = torch.tensor([v * coef + 1.5 for v in x]) plt.plot(x, y1, label='real') plt.grid() plt.legend() plt.show() #使用dataloader构建数据加载器并进行模型构建 # 构造数据集 x, y, coef = create_dataset() # 构造数据集对象 dataset = TensorDataset(x, y) # 构造数据加载器 # dataset=:数据集对象 # batch_size=:批量训练样本数据 # shuffle=:样本数据是否进行乱序 dataloader = DataLoader(dataset=dataset, batch_size=16, shuffle=True) # 构造模型 # in_features指的是输入张量的大小size # out_features指的是输出张量的大小size model = nn.Linear(in_features=1, out_features=1) #设置损失函数和优化器 # 构造平方损失函数 criterion = nn.MSELoss() # 构造优化函数 optimizer = optim.SGD(params=model.parameters(), lr=1e-2) # 模型训练 epochs = 100 # 损失的变化 loss_epoch = [] total_loss = 0.0 train_sample = 0.0 for _ in range(epochs): for train_x, train_y in dataloader: # 将一个batch的训练数据送入模型 y_pred = model(train_x.type(torch.float32)) # 计算损失值 loss = criterion(y_pred, train_y.reshape(-1, 1).type(torch.float32)) total_loss += loss.item() train_sample += len(train_y) # 梯度清零 optimizer.zero_grad() # 自动微分(反向传播) loss.backward() # 更新参数 optimizer.step() # 获取每个batch的损失 loss_epoch.append(total_loss / train_sample) # 绘制损失变化曲线 plt.plot(range(epochs), loss_epoch) plt.title('损失变化曲线') plt.grid() plt.show() # 绘制拟合直线 plt.scatter(x, y) x = torch.linspace(x.min(), x.max(), 1000) y1 = torch.tensor([v * model.weight + model.bias for v in x]) y2 = torch.tensor([v * coef + 1.5 for v in x]) plt.plot(x, y1, label='训练') plt.plot(x, y2, label='真实') plt.grid() plt.legend() plt.show()
如遇报错:AttributeError: module 'backend_interagg' has no attribute 'FigureCanvas'.
解决办法:关闭show plots in tool window
运行代码,结果如下:
浙公网安备 33010602011771号