欧几里得算法-公因子分解

#coding=utf-8

'''
    目标：对公因子实现分解
    gcd(a,b)=xa+by,且x,y均为int,解出x,y的值
    a=bq0+r0
    b=r0q1+r1
    r0=r1q2+r2
    r1=r2q3+r3

    ...
    rn=rn+1qn+2+rn+2
    ri=xia+yib
    xi=xi-2-qixi-1   yi=xi-2-qixi-1
    记录qi 每次的不完全商
    a/b=qi x0=x-2-q0x-1
    x1=x-1-q1x0
    x[i]=x[i-2]-q[i]x[i-1]
    法一：全局列表
    x[-2]=1 x[-1]=0 y[-2]=0 y[-1]=1
    i=2
    x[i]=x[i-2]+q*x[i-1]
    x-2=1 x-1=0 y-2=0 y-1=1


'''
x=[1,0]
y=[0,1]  #可以循环利用

def gcd_x_y(a,b):
    '''
    欧几里得扩展算法+递推公式
    '''
    i,na,nb=2,a,b
    while (a%b):
        r,q=a%b,int(a/b)
        x.append((x[i-2]-q*x[i-1]))
        y.append((y[i-2]-q*y[i-1]))
        a,b,i=b,r,i+1
    print("%d和%d的公因子：%d,x:%d,y:%d"%(na,nb,b,x[i-1],y[i-1]))
gcd_x_y(8142,11766)

示例一的程序存在缺点：没有考虑到a与b的大小关系，会输出两个x,y从而造成不唯一，而实际上是唯一的。

#coding=utf-8

'''
    目标：对公因子实现分解
    gcd(a,b)=xa+by,且x,y均为int,解出x,y的值
    a=bq0+r0
    b=r0q1+r1
    r0=r1q2+r2
    r1=r2q3+r3

    ...
    rn=rn+1qn+2+rn+2
    ri=xia+yib
    xi=xi-2-qixi-1   yi=xi-2-qixi-1
    记录qi 每次的不完全商
    a/b=qi x0=x-2-q0x-1
    x1=x-1-q1x0
    x[i]=x[i-2]-q[i]x[i-1]
    法一：全局列表
    x[-2]=1 x[-1]=0 y[-2]=0 y[-1]=1
    i=2
    x[i]=x[i-2]+q*x[i-1]
    x-2=1 x-1=0 y-2=0 y-1=1


'''
x=[1,0]
y=[0,1]  #可以循环利用

def gcd_x_y(a,b):
    '''
    欧几里得扩展算法+递推公式
    '''
    if(a<b):
        a,b=b,a  #书上的方法默认a>=b,然后计算
    i,na,nb=2,a,b
    while (a%b):
        r,q=a%b,int(a/b)
        x.append((x[i-2]-q*x[i-1]))
        y.append((y[i-2]-q*y[i-1]))
        a,b,i=b,r,i+1
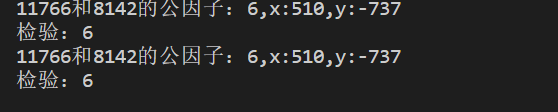
    print("%d和%d的公因子：%d,x:%d,y:%d"%(na,nb,b,x[i-1],y[i-1]))
    print("检验：%d"%(na*x[i-1]+nb*y[i-1]))
gcd_x_y(8142,11766)
gcd_x_y(11766,8142)

#coding=utf-8

'''
    目标：对公因子实现分解
    gcd(a,b)=xa+by,且x,y均为int,解出x,y的值
    a=bq0+r0
    b=r0q1+r1
    r0=r1q2+r2
    r1=r2q3+r3

    ...
    rn=rn+1qn+2+rn+2
    ri=xia+yib
    xi=xi-2-qixi-1   yi=xi-2-qixi-1
    记录qi 每次的不完全商
    a/b=qi x0=x-2-q0x-1
    x1=x-1-q1x0
    x[i]=x[i-2]-q[i]x[i-1]
    法一：全局列表
    x[-2]=1 x[-1]=0 y[-2]=0 y[-1]=1
    i=2
    x[i]=x[i-2]+q*x[i-1]
    x-2=1 x-1=0 y-2=0 y-1=1


'''
x=[1,0]
y=[0,1]  #可以循环利用

def gcd_x_y(a,b):
    '''
    欧几里得扩展算法+递推公式
    '''
    if(a<b):
        a,b=b,a  #书上的方法默认a>=b,然后计算
    i,na,nb=2,a,b
    while (a%b):
        r,q=a%b,int(a/b)
        x.append((x[i-2]-q*x[i-1]))
        y.append((y[i-2]-q*y[i-1]))
        a,b,i=b,r,i+1
    print("%d和%d的公因子：%d,x:%d,y:%d"%(na,nb,b,x[i-1],y[i-1]))
    print("检验：%d*%d+%d*%d=%d"%(na,x[i-1],nb,y[i-1],na*x[i-1]+nb*y[i-1]))
gcd_x_y(8142,11766)