基础算法（2）

高精度加法

（常规只能到10^6次方）

思想：1、大整数存储：每一位存入数组，个位存在前，高位存在后（和常规表示是反的）；

　　　2、模拟手算加法的步骤，进位　

 

#include <iostream>
#include <vector> 
using namespace std;
const int n = 1000010; 

vector<int> add(vector<int> &A, vector<int> &B)
{
    vector<int> C; 
    int t = 0 ; //进位
    for(int i=0; i<A.size() || i<B.size(); i++ )
    {
        if( i<A.size()) t+=A[i];
        if( i<B.size()) t+=B[i];
        C.push_back( t%10 ); 
        t /= 10; 
     } 
     if(t) C.push_back(1);
     return C;
}

int main() {
    
    string a,b ; //太长了，用字符串读 
    vector<int> A,B,C;
    
    cin>>a>>b; 
    for(int i=a.size()-1 ; i>=0; i--)    //逆序 
        A.push_back(a[i]-'0'); //A = [6,5,4,3] 
    for(int i=b.size()-1 ; i>=0; i--) 
        B.push_back(b[i]-'0');
    
    C = add(A,B);  //进行加法 
    
    for (int i=C.size()-1 ; i>=0; i--) //输出结果 
        printf("%d", C[i]);
        
    return 0;
}

 

 

 

高精度减法

思想上差不多，但是借位方面较为麻烦，另外需要考虑两个数相减的为”大数“-”小数“来得到绝对值，而结果的正负另外判断：

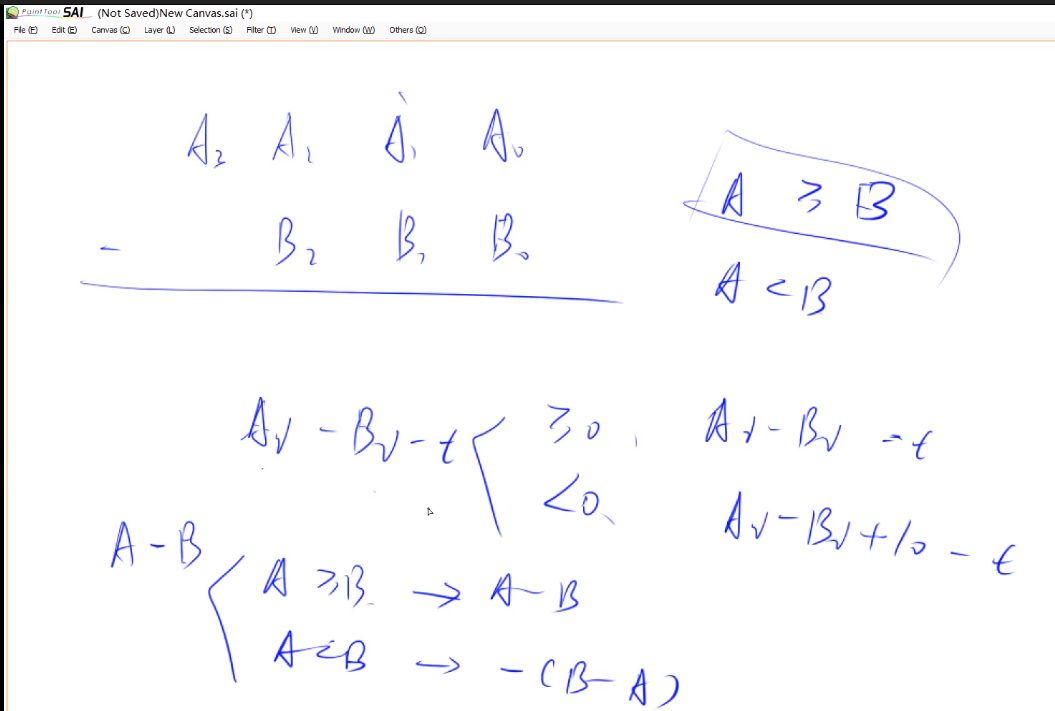
#include <iostream>
#include <vector> 
using namespace std;
const int n = 1000010; 

// 判断是否 A>=B 
bool cmp(vector<int> &A, vector<int> &B)
{
    if( A.size() != B.size() ) return A.size() > B.size();
    for( int i = A.size() - 1; i>=0; i--)
        if (A[i]!=B[i]) 
            return  A[i]>B[i] ; 
    return true;
}

vector<int> sub(vector<int> &A, vector<int> &B )
{
    vector<int> C ; 
    int t = 0;  
    for( int i=0 ; i<A.size(); i++) //默认 A>=B
    {
        t = A[i]-t ;
        if( i<B.size()) t-=B[i];
        C.push_back((t+10)%10);
        if( t<0 ) t=1; //发生借位 
        else t=0;     //没有借位 
    } 
    //对于类似的结果003，删除前导0 
    while (C.size() > 1 && C.back() == 0) C.pop_back();
    
    return C; 
}

int main() {
    
    string a,b ; //太长了，用字符串读 
    vector<int> A,B,C;
    
    cin>>a>>b; 
    for(int i=a.size()-1 ; i>=0; i--)    //逆序 
        A.push_back(a[i]-'0'); //A = [6,5,4,3] 
    for(int i=b.size()-1 ; i>=0; i--) 
        B.push_back(b[i]-'0');
    
    if(cmp(A,B)) 
        C = sub(A,B); 
    else
    {
        C = sub(B,A);
        printf("-");
    }
    
    for (int i=C.size()-1 ; i>=0; i--) //输出结果 
        printf("%d", C[i]);
        
    return 0;
}

高精度乘法

 

与加法类似，这里实现的是“较大数”X“较小数”

 

#include <iostream>
#include <vector> 
using namespace std;
const int n = 1000010; 

vector<int> mul(vector<int> &A, int b)
{
    vector<int> C ; 
    int t = 0 ;
    for( int i =0; i<A.size() || t!=0 ; i++ )
    {
        if(i<A.size()) t+=A[i]*b ; 
        C.push_back(t%10);
        t /= 10;
    }
    
    while(C.size()>1 && C.back()==0 ) C.pop_back();
    
    return C; 
}

int main() {
    
    string a; //较大数 
    int b; //较小数 
    vector<int> A,C;
    
    cin>>a>>b; 
    for(int i=a.size()-1 ; i>=0; i--)    //逆序 
        A.push_back(a[i]-'0'); //A = [6,5,4,3] 
    
    C = mul(A,b) ;
    
    for (int i=C.size()-1 ; i>=0; i--) //输出结果 
        printf("%d", C[i]);
        
    return 0;
}

 

高精度除法

 先上图：

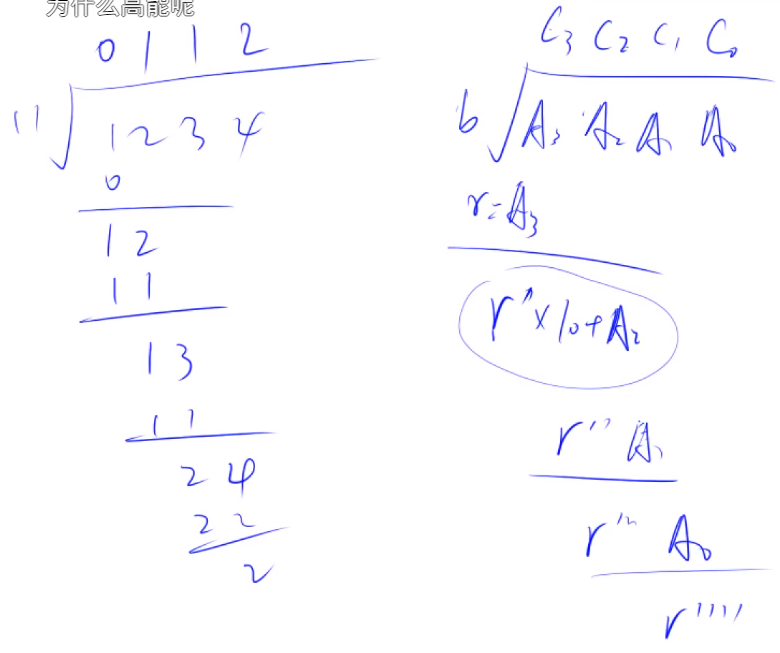
具体代码：

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std ; 

vector<int> div(vector<int> &A , int b, int &t)
{
    vector<int> C; 
    t=0;
    for(int i=A.size()-1 ; i>=0 ; i-- )
    {
        t=t*10+A[i]; 
        C.push_back(t/b); 
        t%=b ; 
    }
    reverse(C.begin(), C.end());
    while(C.size()>1 && C.back()==0) C.pop_back();
    return C; 
}

int main(){
    vector<int> A,C ; 
    string a;  int b,r ;
    cin>>a>>b ; 
    for(int i=a.size()-1; i>=0;i--) A.push_back(a[i]-'0'); 
    C = div(A,b,r); 
    for(int i=C.size()-1; i>=0;i--) printf("%d",C[i]);
    cout<<endl<<r;
    return 0;
}

 

前缀和

核心： S[i+1] = s[i] + a[i+1] ; 

 

             a[left] +... +a[right] = S[r] - S[l-1]

计算区间和：

 

#include <iostream>
using namespace std ; 

const int N = 1e6+10;
int q[N],S[N];


int main(){
    int n,m;
    cin>>n>>m; 
    for(int i=1; i<=n ;i++) cin>>q[i]; 
    for(int i=1; i<=n; i++) S[i]=S[i-1]+q[i];
    while(m--)
    {
        int l,r; 
        cin>>l>>r;
        cout<<S[r]-S[l-1]<<endl;
    }
    
    return 0;
}

 

对于二维（矩阵）形式的前缀和，

核心：S22 - S21 - S12 + S11 

 

　　　Sij =  Si-1,j + Si,j-1 - Si-1,j-1 + aij

 区间和的计算：

#include <iostream>
using namespace std ; 

const int N = 1e3+10;
int a[N][N],S[N][N];
int n,m,q;

int main(){
    cin>>n>>m>>q; 
    for(int i=1; i<=n;i++)
        for(int j=1;j<=m;j++)
        {
            scanf("%d",&a[i][j]);
            S[i][j] += S[i][j-1]+S[i-1][j]-S[i-1][j-1]+a[i][j];
        }
    while(q--)
    {
        int x1,y1,x2,y2;
        scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
        printf("%d\n", S[x2][y2] - S[x1-1][y2] - S[x2][y1-1] + S[x1-1][y1-1]) ;
    }
    return 0;
}

差分

本质上是前缀和的逆运算

作用：O(n)的范围内，达到 A->B

 

#include <iostream>
using namespace std ; 

const int N = 1e6+10;
int n,m,a[N],b[N]; 

void Insert(int l, int r, int c)
{
    b[l]+=c; 
    b[r+1]-=c; 
}

int main(){
      cin>>n>>m ; 
      for(int i=1;i<=n;i++) cin>>a[i]; // 1 2 3 4
      for(int i=1;i<=n;i++) Insert(i,i,a[i]);    //插入 1 2-1 3-2 4-3
    while(m--)
    {
        int l,r,c;  
        scanf("%d%d%d",&l,&r,&c) ;    // 1 2 1 
        Insert(l,r,c);                 // 1 1 1 1 -> 1 2 1 0
    } 
    for(int i=1; i<=n;i++) b[i]+=b[i-1]; //1 3 4 4
    for(int i=1; i<=n;i++) printf("%d ",b[i]);
    return 0;
}

二维：

#include <iostream>
using namespace std ; 

const int N = 1e3+10;
int n,m,q,a[N][N],b[N][N]; 

void insert(int x1, int y1,int x2,int y2, int c)
{
    b[x1][y1] += c ; 
    b[x1][y2+1] -= c ; 
    b[x2+1][y1] -= c ; 
    b[x2+1][y2+1] += c ;
}

int main(){
       
      cin>>n>>m>>q; 
      for(int i=1;i<=n;i++)
          for(int j=1; j<=m; j++)
              {
                  cin>>a[i][j]; 
                  insert(i,j,i,j,a[i][j]);
            }
          
      while(q--)
      {
          int x1,y1,x2,y2,c; 
          cin>>x1>>y1>>x2>>y2>>c; 
          insert(x1,y1,x2,y2,c);
    }
    
    for(int i=1; i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            b[i][j] += b[i][j-1] + b[i-1][j] - b[i-1][j-1];
            cout<<b[i][j]<<' ';
        }
        cout<<endl;
    }
    return 0;
}