基础算法（1）

快速排序（O(NlogN)）

思路：确定分界点（序列里随机一个数都可以）：左边界、右边界、中值；调整范围；递归处理左、右两段

核心：每次j指针落在i指针前面位置时，将q[i]、q[j]进行swap操作（先分两边，再递归左右）

y总讲解的图示：

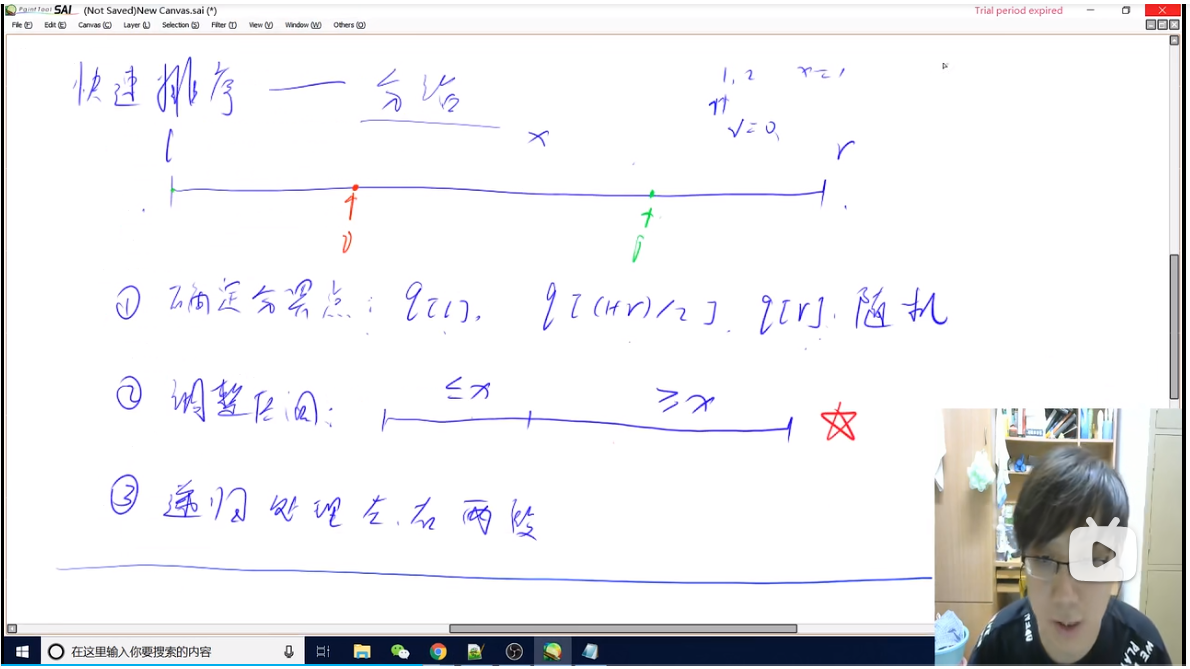
代码模板：

#include <iostream>
using namespace std;

// 快速排序 
const int N = 1e6+10;

int n,q[N]; // 规模 开辟空间大小 

void quick_sort(int q[], int left, int right)
{
    if (left >= right) return;   //判断边界 
    
    int x=q[left+right >> 1]; //x是判定条件 
    int i=left-1, j=right+1 ; 
    while(i<j) //每次移动并交换 
    {
        do i++; while( q[i]<x); //对比目标，希望将i移到x右边
        do j--; while( q[j]>x); //对比目标，希望将j移到x左边
        if (i<j) swap(q[i], q[j]);    //出现问题，那就交换
    }    
    
    quick_sort(q, left, j);  //递归左半部分 
    quick_sort(q, j+1, right);//递归右半部分 
}

int main() {
    
    scanf("%d", &n);
    
    for(int i=0; i<n ; i++)
        scanf("%d", &q[i]);
    
    quick_sort(q, 0, n-1);
    
    for(int i=0; i<n; i++)
        printf("%d ", q[i]);
    
    return 0;
}

归并排序（O(NlogN)）

思路：确定分界点（中值）；递归排序左右边；将有序数组合并成有序数组（归并）；

核心：分界点为中心点，也是双指针算法i、j（先递归左右，再分左右）

代码模板：

#include <iostream>
using namespace std;

// 归并排序 
const int N = 1e6+10;
int n,q[N],newarray[N]; // 规模 开辟空间大小 

// 图示 l_____mid______r
//        l_____mid
//         mid_____r

void merge_sort(int q[], int left, int right)
{
    if (left >= right) return; 
    
    int mid = left+right >> 1 ;  
    merge_sort(q, left, mid);  //递归左半部分 
    merge_sort(q, mid+1, right);//递归右半部分 
    
    int k=0, i=left, j=mid+1;
    while( i<=mid && j<=right)
        if (q[i]<=q[j]) newarray[k++]=q[i++]; //上 > 下，上面的放到新数组
        else newarray[k++]=q[j++];    //否则下面的放到新数组 
    
    while( i<=mid) newarray[k++]=q[i++];//剩余没排序完的直接加入新数组 
    while( j<=right) newarray[k++]=q[j++];
    
    for (i=left, j=0; i<=right; i++,j++)
        q[i] = newarray[j];        //把新数组copy到原数组里面 
}

int main() {
    
    scanf("%d", &n);
    
    for(int i=0; i<n ; i++)
        scanf("%d", &q[i]);
    
    merge_sort(q, 0, n-1);
    
    for(int i=0; i<n; i++)
        printf("%d ", q[i]);
    
    return 0;
}

习题（788.逆序对的数目）

题目：给定一个长度为

这个题就是在每次归并排序中，对于“上面的<下面的”情况（else），计算（mid+1）-（i）

例如序列：2 3 4 5 6 1，在最后的递归中，序列应该排序成了这样子：2 3 4 1 5 6

此时，mid+1相当于是右半部分的起点，而i是判定位置，两者之差就是逆序对的数量。

具体代码如下：（本题被y总修改过，int会爆掉，可以采用long long）

#include <iostream>
using namespace std;

const int N = 1000010 ; 
long long n,q[N],newarray[N],ans=0; 

long long merge_sort(long long q[],long long l,long long r)
{
    if(l>=r) return 0;
    long mid = (l+r)/2;
    ans = merge_sort(q, l, mid)+merge_sort(q, mid+1, r);
    
    int k=0;
    int i=l, j=mid+1;
    while( i<=mid && j<=r )
    {
        if( q[i]<=q[j] ) newarray[k++] = q[i++];
        else
        {
           ans += mid-i+1 ;
           newarray[k++] = q[j++]; 
        }
    } 
    while(i<=mid) newarray[k++]=q[i++];
    while(j<=r) newarray[k++]=q[j++];   
    
    for ( i=l,j=0; i<=r; i++,j++ ) 
    {
        q[i] = newarray[j];
    }
    
    return ans;
}

int main(){
    
    cin>>n ;
    
    for( int i=0; i<n; i++ ) cin>>q[i];
    
    ans = merge_sort(q, 0, n-1);
    
    cout<<ans<<endl;
    
    return 0;
}

二分

整数二分：设定中值；左、右边界点与中值比较；

（1）mid = （left + right + 1）/ 2 ； true后面是l=mid，此时必须+1，防止当left=right-1时，程序发生死循环

（2）mid = （left + right）/ 2 ；

思路：在一个区间内部，每次选择一个答案所在的区间进行处理，每次都要保证区间内有答案。当区间长度为1时，区间内的数一定是答案。

图示：

模板代码：

#include <iostream>
using namespace std;
const int N = 100010 ;
int n,m, q[N];  
// 二分查找 有序数列中某数的始末坐标
// 1 1 2 2 3 3 4 中 3的输出为 4 5 

int main() {
    
    cin>>n>>m ; 
    
    for(int i=0; i<n; i++ ) cin>>q[i]; 
    
    while(m--)
    {
        int x; cin>>x; 
        int left=0, right=n-1; 
        
        while(left<right)
        {
            int mid=left+right>>1;
            if(q[mid] >= x) right=mid;
            else left=mid+1;
        }
        
        if (q[left] != x ) cout<<"-1 -1"<<endl;//没找到 
        else
        {
            cout<<left<<' '; 
            
            int left = 0, right = n-1; 
            while(left<right)
            {
                int mid = left+right+1 >> 1 ;
                if (q[mid] <= x) left=mid; 
                else right=mid-1 ; 
            }
            cout<<left<<endl;
        }
    }
    
    return 0;
}

浮点数二分：本质与整数二分相同，不需要处理边界，相对来说更简单

模板代码：（找平方根）

#include <iostream>
using namespace std;
const int N = 100010 ;
int n, q[N];  

int main() {
    
    double l, r; 
    double x; 
    cin >> x;
    
    while(r-l > 1e-8) //浮点数切忌 == 
    {
        double mid = (l+r)/2 ; 
        if ( mid*mid >= x ) r=mid ; 
        else l = mid ; 
    } 
    
    printf("%1f\n", l);
    return 0;
}

习题（790.数的三次方根）

题目：给定一个浮点数n

具体代码如下：

#include <iostream>
#include <cmath>
#include <iomanip>
using namespace std;
const int N = 100010;

int main(){
    
    double n;
    bool flag=true; 
    cin>>n; 
    if(n<0) flag = false;//输入有可能是负数
    double l=0, r=N; //r指定一个常数
   
    while( r-l > 1e-8)
    { 
        double mid = (l+r)/2;
        if( pow(mid,3) > abs(n) ) r=mid; 
        else l=mid;
    }
    if(!flag) cout<<'-'; //负数加‘-’
    cout<<fixed<<setprecision(6)<<l;
}

posted @ 2023-03-05 23:16 尊滴菜阅读(28) 评论(0) 收藏举报

刷新页面返回顶部

闲时记录

——岁月无从贷款

基础算法（1）

公告