数据结构与算法之插入排序与归并排序
插入排序
插入排序举个最好的例子就是扑克牌,当我们手里拿了N张无序的牌,如果要对牌进行排序,最好的思路是从第二张开始,我们设置这个为i,让它和前边的牌做比较如果需要换位置就换,换了以后继续往前在看需不需要换。如果i-x牌不需要和i交换
则终止,然后i向后移动,直到手里的扑克牌到最后一张也跟前边的依次对比过了。所以插入排序就是个双层循环。此算法的时间复杂度为O(n^2)
public static int[] charu(int[] arr) {
for (int i = 1; i < arr.length; i++) {
for (int j = i; j > 0; j--) {
int left = arr[j - 1];
int right = arr[j];
if (right < left) {
int temp = left;
arr[j - 1] = right;
arr[j] = left;
} else {
break;
}
}
}
return arr;
}

归并排序
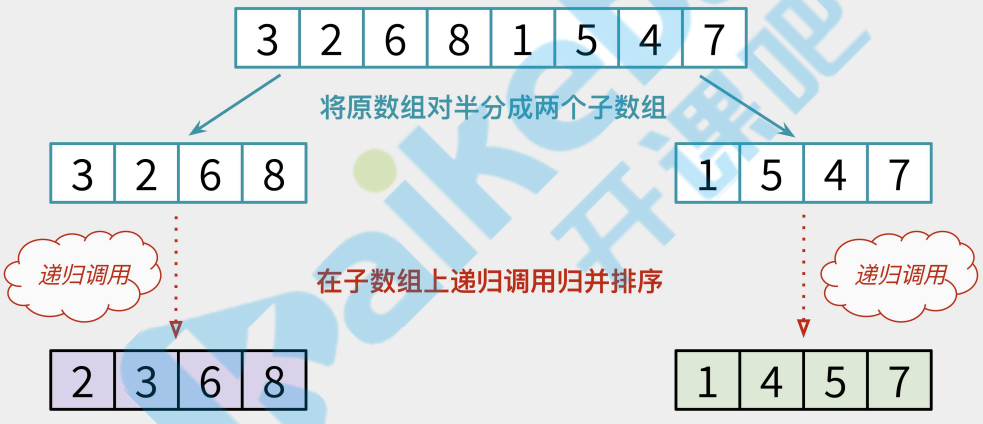
归并排序像是它的名字一样,先将数据归类,然后合并.以下归并排序先将源数组递归拆分,一直拆到数组中只包含一个元素.一个简单的例子.数组长度是2,将数组拆分为left和right两个数组,然后对这两个数组
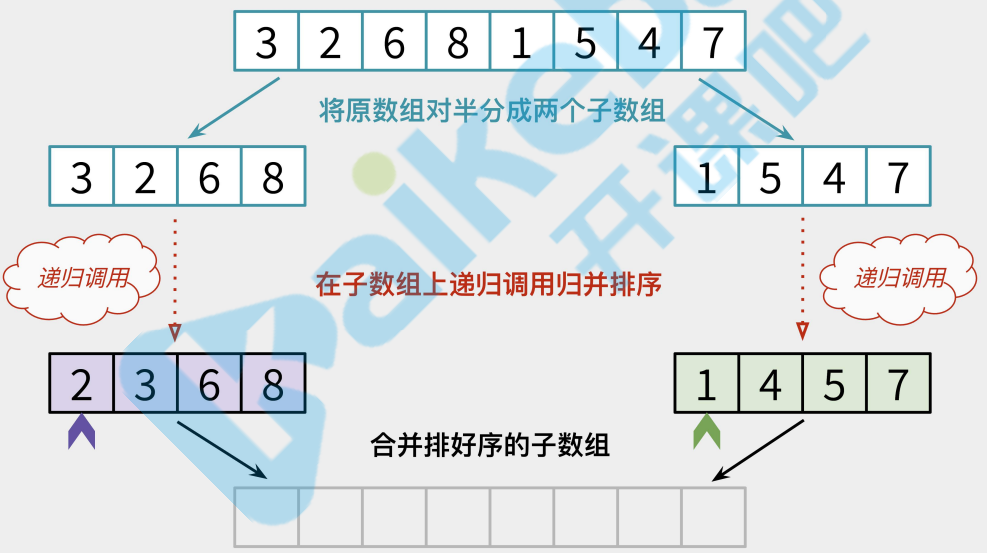
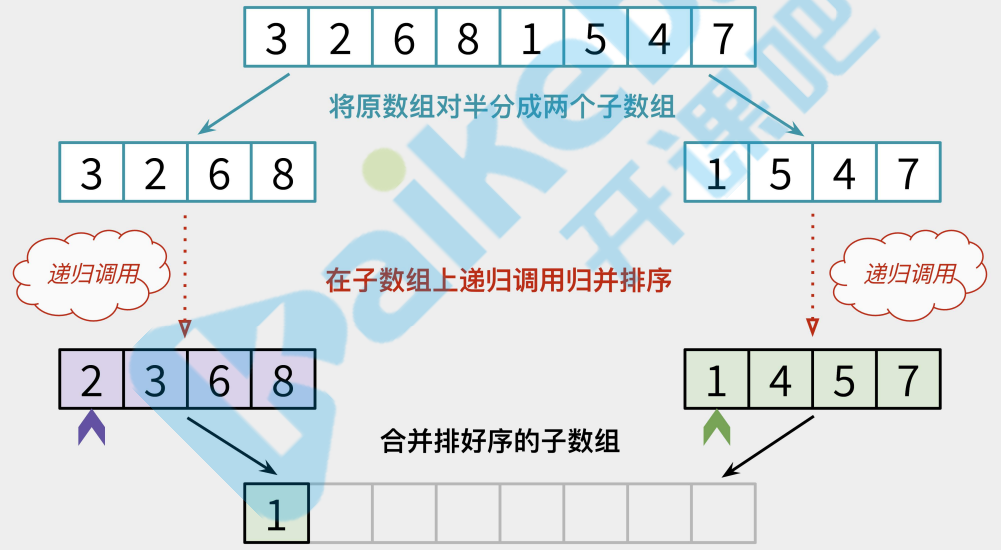
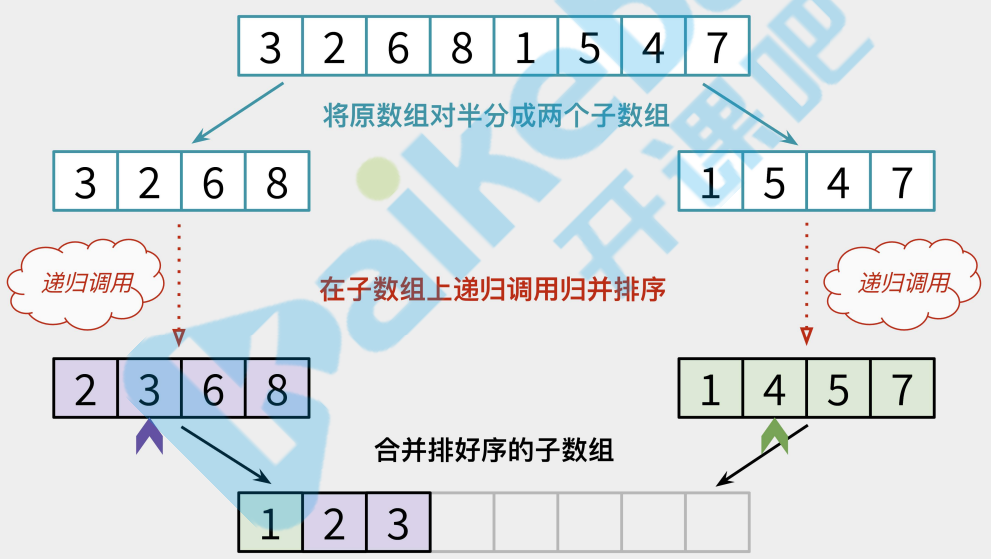
进行合并.合并的操作稍微复杂,核心思路是用A数组的元素依次和B数组对比,如果发现A[0]比B[0]大则将B[0]添加到新数组C中,同时B数组的指针右移一位,直到B[N]比A[0]大.如果是A[0]比B[0]小,则将A[0]
添加到数组C中,移动A.最后如果A或B有一个数组已经到达末尾,则将另一个数组的剩下元素转义到数组C中.此算法的时间复杂度为O(nlogn)
//归并排序
public static int[] guibing(int[] arr) {
if (arr.length <= 1) {
return arr;
}
int[] left = guibing(Arrays.copyOfRange(arr, 0, arr.length / 2));
int[] right = guibing(Arrays.copyOfRange(arr, arr.length / 2, arr.length));
return merge(left, right);
}
private static int[] merge(int[] left, int[] right) {
int[] longArr = left;
int[] shortArr = right;
if (left.length < right.length) {
longArr = right;
shortArr = left;
}
int[] result = new int[longArr.length + shortArr.length];
int shortIndex = 0;
int longIndex = 0;
int resultIndex = 0;
while (shortIndex < shortArr.length && longIndex < longArr.length) {
if (shortArr[shortIndex] < longArr[longIndex]) {
result[resultIndex] = shortArr[shortIndex];
resultIndex++;
shortIndex++;
} else {
while (longIndex < longArr.length && shortArr[shortIndex] >= longArr[longIndex]) {
result[resultIndex] = longArr[longIndex];
resultIndex++;
longIndex++;
}
}
}
if (shortIndex != shortArr.length) {
System.arraycopy(shortArr, shortIndex, result, resultIndex, shortArr.length - shortIndex);
}
if (longIndex != longArr.length) {
System.arraycopy(longArr, longIndex, result, resultIndex, longArr.length - longIndex);
}
return result;
}
以下是一个测试方法,保证了以上归并排序的准确性.
public static void main(String[] args) {
Random random = new Random();
while (true) {
int length = random.nextInt(100);
int[] arr = new int[length];
for (int x = 0; x < length; x++) {
arr[x] = random.nextInt(100);
}
int[] guibing = guibing(arr);
Arrays.sort(arr);
boolean equals = Arrays.equals(guibing, arr);
System.out.println(equals);
if (!equals) {
break;
}
}
}
拆分流程
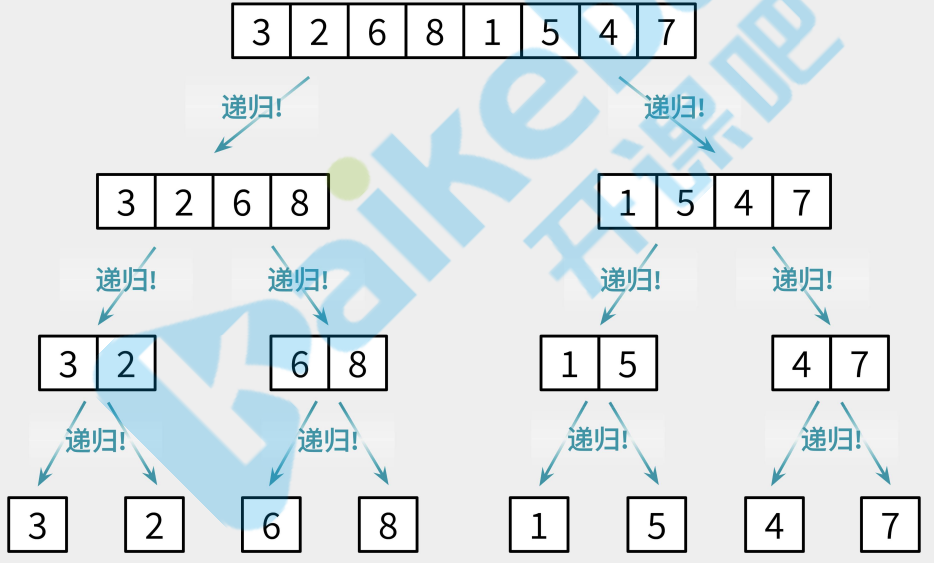
合并流程
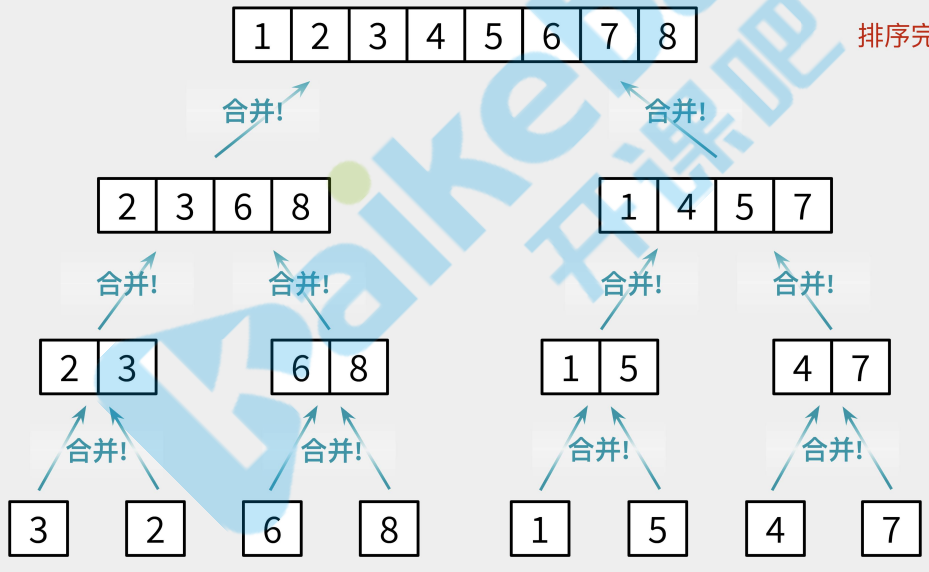
合并过程中两个数组对比