集美大学课程实验报告-实验4:树、二叉树与查找
| 项目名称 | 内容 |
|---|---|
| 课程名称 | 数据结构 |
| 班级 | 网安2411 |
| 指导教师 | 郑如滨 |
| 学生姓名 | 马梦佳 |
| 学号 | 202321514092 |
| 实验项目名称 | 实验4:树、二叉树与查找 |
| 上机实践日期 | 2025年4月17日 |
| 上机实践时间 | 4学时 |
一、目的(本次实验所涉及并要求掌握的知识点)
-学习并掌握二叉树的基本操作,包括创建、遍历(先序、层次)、求高度等
-熟练掌握熟练掌握树的递归结构及在其上的递归算法
-掌握二叉排序树(BST)的搜索、创建与删除操作
-运用哈希表解决实际问题,理解哈希表的工作原理,掌握哈希函数设计与冲突处理方法
二、实验内容与设计思想
题目1:(PTA编程)先序序列创建二叉树
主要内容:实现一个函数,删除顺序表中指定区间内的元素。
函数相关伪代码
结构体 BiTNode
数据成员
char data
BiTNode* lchild
BiTNode* rchild
函数 CreateBTree(string s, int index)
如果 index >= s.size() 或 s[index] == '#'
index = index + 1
返回 nullptr
创建一个新的 BiTNode 节点 node
node.data = s[index]
index = index + 1
node.lchild = CreateBTree(s, index)
node.rchild = CreateBTree(s, index)
返回 node
函数 InOrder(BTree root)
如果 root 为空
返回
调用 InOrder(root.lchild)
输出 root.data
调用 InOrder(root.rchild)
主函数 main
循环读取输入字符串 s
初始化 index = 0
调用 CreateBTree(s, index) 创建二叉树
调用 InOrder(root) 中序遍历二叉树并输出
输出换行符
函数代码
#include <iostream>
#include <string>
using namespace std;
typedef struct BiTNode {
char data;
struct BiTNode *lchild, *rchild;
} BTNode, *BTree;
BTree CreateBTree(string &s, int &index) {
if (index >= s.size() || s[index] == '#') {
index++;
return nullptr;
}
BTNode* node = new BTNode();
node->data = s[index];
index++;
node->lchild = CreateBTree(s, index);
node->rchild = CreateBTree(s, index);
return node;
}
void InOrder(BTree root) {
if (!root) return;
InOrder(root->lchild);
cout << root->data << " ";
InOrder(root->rchild);
}
int main( ) {
string s;
while (getline(cin, s) && !s.empty()) {
int index = 0;
BTree root = CreateBTree(s, index);
InOrder(root);
cout << endl;
}
string name, num;
cout << "姓名:";
cin >> name;
cout << "学号:";
cin >> num;
return 0;
}
时间复杂度与空间复杂度
- 时间复杂度:O(n)
- 空间复杂度:O(logn)
题目2:(PTA函数)先序输出叶结点
主要内容:按照先序遍历的顺序输出给定二叉树的叶结点。
函数相关伪代码
函数 PreorderPrintLeaves(BinTree BT)
如果 BT 为空
返回
如果 BT.Left 为空 且 BT.Right 为空
输出 BT.Data
调用 PreorderPrintLeaves(BT.Left)
调用 PreorderPrintLeaves(BT.Right)
函数代码
void PreorderPrintLeaves( BinTree BT ) {
if (BT == NULL) {
return;
}
if (BT->Left == NULL && BT->Right == NULL) {
printf(" %c", BT->Data);
}
PreorderPrintLeaves(BT->Left);
PreorderPrintLeaves(BT->Right);
}
时间复杂度与空间复杂度
- 时间复杂度:O(n)
- 空间复杂度:O(logn)
题目3:(PTA函数)求二叉树高度
主要内容:要求给定二叉树的高度。
函数相关伪代码
函数 GetHeight(BinTree BT)
如果 BT 为空
返回 0
leftHeight = GetHeight(BT.Left)
rightHeight = GetHeight(BT.Right)
返回 max(leftHeight, rightHeight) + 1
函数代码
int GetHeight(BinTree BT) {
if (BT == NULL) {
return 0;
}
int leftHeight = GetHeight(BT->Left);
int rightHeight = GetHeight(BT->Right);
return (leftHeight > rightHeight ? leftHeight : rightHeight) + 1;
}
时间复杂度与空间复杂度
- 时间复杂度:O(n)
- 空间复杂度:O(logn)
题目4:(PTA编程)二叉树层次遍历(广度优先)
主要内容:层次遍历树中所有节点。
函数相关伪代码
结构体 BiTNode
数据成员
char data
BiTNode* lchild
BiTNode* rchild
函数 createTree(string s, int i)
如果 i >= s.size() 或 s[i] == '#'
返回 nullptr
创建一个新的 BiTNode 节点 node
node.data = s[i]
node.lchild = createTree(s, 2 * i)
node.rchild = createTree(s, 2 * i + 1)
返回 node
函数 levelOrder(BTree T)
如果 T 为空
输出 "NULL"
返回
创建一个队列 q
将 T 加入队列 q
创建一个向量 res
当队列 q 不为空
弹出队列 q 的队头节点 node
将 node.data 加入 res
如果 node.lchild 不为空
将 node.lchild 加入队列 q
如果 node.rchild 不为空
将 node.rchild 加入队列 q
遍历 res
如果不是第一个元素
输出空格
输出 res[i]
主函数 main
读取一行输入字符串 s
初始化 root 为 nullptr
如果 s 的长度大于 1
调用 createTree(s, 1) 创建二叉树
调用 levelOrder(root) 层序遍历二叉树并输出
函数代码
#include <iostream>
#include <string>
#include <queue>
#include <vector>
using namespace std;
typedef struct BiTNode {
char data;
struct BiTNode *lchild, *rchild;
} BTNode, *BTree;
BTree createTree(const string& s, int i) {
if (i >= s.size() || s[i] == '#') {
return nullptr;
}
BTree node = new BTNode();
node->data = s[i];
node->lchild = createTree(s, 2 * i);
node->rchild = createTree(s, 2 * i + 1);
return node;
}
void levelOrder(BTree T) {
if (T == nullptr) {
cout << "NULL";
return;
}
queue<BTree> q;
q.push(T);
vector<char> res;
while (!q.empty()) {
BTree node = q.front();
q.pop();
res.push_back(node->data);
if (node->lchild) q.push(node->lchild);
if (node->rchild) q.push(node->rchild);
}
for (size_t i = 0; i < res.size(); ++i) {
if (i != 0) cout << " ";
cout << res[i];
}
}
int main() {
string s;
getline(cin, s);
BTree root = nullptr;
if (s.size() > 1) {
root = createTree(s, 1);
}
levelOrder(root);
return 0;
}
时间复杂度与空间复杂度
- 时间复杂度:O(n)
- 空间复杂度:O(n)
题目5:
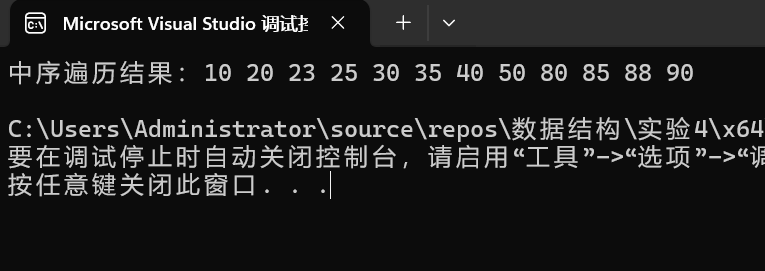
主要内容:给定一串50 30 80 20 40 90 10 25 35 85 23 88 #创建二叉排序树并对其进行中序遍历。
函数相关伪代码
结构体 TNode
数据成员
ElementType Data
BinTree Left
BinTree Right
函数 NewNode(ElementType data)
创建一个新的 TNode 节点 node
node.Data = data
node.Left = NULL
node.Right = NULL
返回 node
函数 Insert(BinTree BST, ElementType X)
如果 BST 为空
返回 NewNode(X)
如果 X < BST.Data
BST.Left = Insert(BST.Left, X)
否则如果 X > BST.Data
BST.Right = Insert(BST.Right, X)
返回 BST
函数 InorderTraversal(BinTree BST)
如果 BST 不为空
调用 InorderTraversal(BST.Left)
输出 BST.Data
调用 InorderTraversal(BST.Right)
主函数 main
定义一个整数数组 values
计算数组长度 n
初始化 BST 为 NULL
遍历数组 values
调用 Insert(BST, values[i]) 构建二叉排序树
输出 "中序遍历结果:"
调用 InorderTraversal(BST) 输出中序遍历结果
输出换行符
函数代码
#include <stdio.h>
#include <stdlib.h>
typedef int ElementType;
typedef struct TNode* Position;
typedef Position BinTree;
struct TNode {
ElementType Data;
BinTree Left;
BinTree Right;
};
BinTree NewNode(ElementType data) {
BinTree node = (BinTree)malloc(sizeof(struct TNode));
node->Data = data;
node->Left = NULL;
node->Right = NULL;
return node;
}
BinTree Insert(BinTree BST, ElementType X) {
if (BST == NULL) {
return NewNode(X);
}
if (X < BST->Data) {
BST->Left = Insert(BST->Left, X);
}
else if (X > BST->Data) {
BST->Right = Insert(BST->Right, X);
}
return BST;
}
void InorderTraversal(BinTree BST) {
if (BST) {
InorderTraversal(BST->Left);
printf("%d ", BST->Data);
InorderTraversal(BST->Right);
}
}
int main() {
int values[] = { 50, 30, 80, 20, 40, 90, 10, 25, 35, 85, 23, 88 };
int n = sizeof(values) / sizeof(values[0]);
BinTree BST = NULL;
for (int i = 0; i < n; i++) {
BST = Insert(BST, values[i]);
}
printf("中序遍历结果:");
InorderTraversal(BST);
printf("\n");
return 0;
}
时间复杂度与空间复杂度
- 时间复杂度:O(nlogn)
- 空间复杂度:O(n)
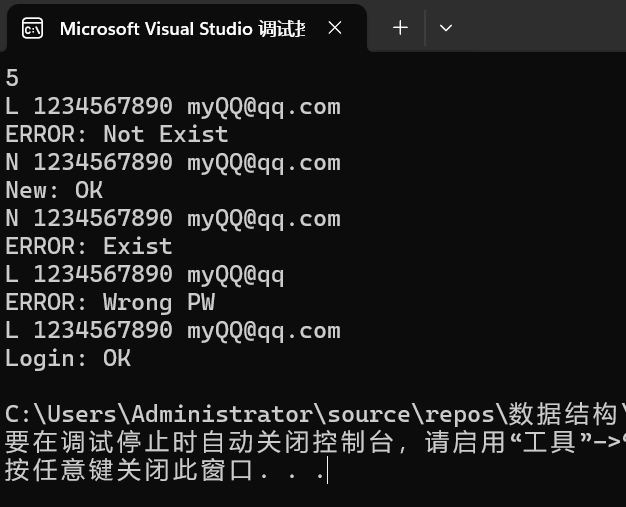
题目6:(哈希表的应用)QQ账户查询
主要内容:。
函数相关伪代码
主函数 main
读取输入 N
创建一个哈希表 accounts
循环 N 次
读取命令 cmd 和字符串 qq, pw
如果 cmd 是 'N'
如果 accounts 中存在键 qq
输出 "ERROR: Exist"
否则
在 accounts 中插入键值对 (qq, pw)
输出 "New: OK"
否则如果 cmd 是 'L'
在 accounts 中查找键 qq
如果找不到键 qq
输出 "ERROR: Not Exist"
否则如果 找到的值不等于 pw
输出 "ERROR: Wrong PW"
否则
输出 "Login: OK"
函数代码
#include <iostream>
#include <string>
#include <unordered_map>
using namespace std;
int main() {
int N;
cin >> N;
unordered_map<string, string> accounts;
for (int i = 0; i < N; i++) {
char cmd;
string qq, pw;
cin >> cmd >> qq >> pw;
if (cmd == 'N') {
if (accounts.find(qq) != accounts.end()) {
cout << "ERROR: Exist" << endl;
} else {
accounts[qq] = pw;
cout << "New: OK" << endl;
}
} else if (cmd == 'L') {
auto it = accounts.find(qq);
if (it == accounts.end()) {
cout << "ERROR: Not Exist" << endl;
} else if (it->second != pw) {
cout << "ERROR: Wrong PW" << endl;
} else {
cout << "Login: OK" << endl;
}
}
}
return 0;
}
时间复杂度与空间复杂度
- 时间复杂度:O(n)
- 空间复杂度:O(n)
三、实验使用环境(本次实验所使用的平台和相关软件)
- 操作系统:Windows 11
- 编程语言:C++
- 开发工具:Visual Studio 2022
- 编译器:C/C++ 17.13
四、实验步骤和调试过程(实验步骤、测试数据设计、测试结果分析)
题目1:(PTA编程)先序序列创建二叉树
本机运行截图
PTA提交截图
题目2:(PTA函数)先序输出叶结点
本机运行截图

PTA提交截图
题目3:(PTA函数)求二叉树高度
本机运行截图

PTA提交截图

题目4:(PTA编程)二叉树层次遍历(广度优先)
本机运行截图

PTA提交截图

题目5:创建二叉排序树并遍历
本机运行截图
题目6:(哈希表的应用)QQ账户查询
本机运行截图
PTA提交截图
![PTA提交截图]()
五、实验小结(实验中遇到的问题及解决过程、实验体会和收获)
遇到的问题及解决方法:
- 问题:在使用先序序列创建二叉树时,没有正确处理“#”,导致程序栈溢出或死循环。
- 解决方法:当遇到#时返回空节点,否则创建新节点并递归构建左右子树。
- 问题:刚开始判断叶节点时只用了左子树为空,未检查右子树是否也为空,导致误判。
- 解决方法:修改判断条件为 root->left == NULL && root->right == NULL,确保是真正意义上的叶节点。
- 问题:在插入节点到二叉排序树时,对于插入位置的判断存在错误,导致树的结构不符合二叉排序树的性质。
- 解决方法:通过增加对查找失败情况的判断和处理,完善了查找功能。
实验体会和收获:
- 通过这次实验,掌握了如何根据先序序列递归创建二叉树,以及如何通过递归和队列实现二叉树的各种遍历操作,学会了二叉排序树的创建和中序遍历算法,理解了二叉排序树的性质和操作原理,学会了如何使用哈希表实现快速查询功能,并能够根据实际需求设计合适的哈希表存储结构。
- 在实验过程中,我学会了使用 Visual Studio 的调试功能,通过设置断点、单步调试,逐步跟踪程序执行流程,对二叉树的创建、遍历等操作有了更深刻的理解。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号