关于Levenshtein Distance的一些简单拓展
Levenshtein Distance,也被称为Edit Distance,即编辑距离,一般用它来表示两个字符串的差异程度,它指的是一个字符串s由删除,插入,修改而变成另一个字符串t的最短操作。
一、基础编辑距离问题。
题目地址:https://www.luogu.com.cn/problem/P2758
题目描述:给定两个字符串,问编辑距离。
解答:用两个for循环,dp[i][j]表示第一个字符串运行到i,第二个字符串运行到j的编辑距离,edit distance的一般递推形式如下。
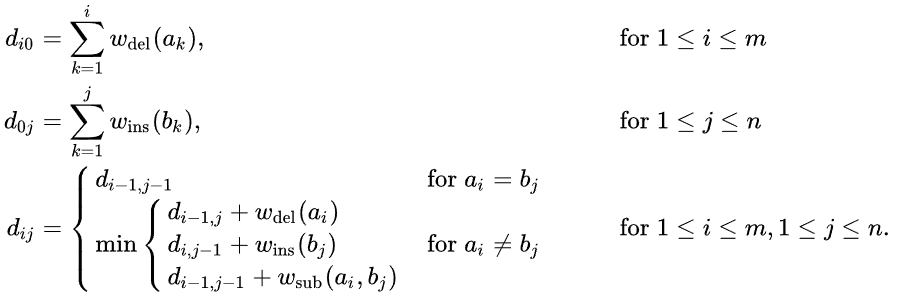 (摘自wiki)
(摘自wiki)

inline int solve(string s1,string s2) { int ar[2010][2010]; memset(ar,0,sizeof(ar)); int m=s1.size(); int n=s2.size(); for (int i=0;i<=n;i++) ar[0][i]=i; for (int i=0;i<=m;i++) ar[i][0]=i; for (int i=1;i<=m;i++) { for (int j=1;j<=n;j++) { ar[i][j]=min(min(ar[i][j-1]+1,ar[i-1][j]+1),ar[i-1][j-1]+(s1[i-1]==s2[j-1] ? 0 : 1)); } } return ar[m][n]; }
另外 ,Edit Distance 满足三角不等式,即dis(A,B)+dis(B,C)>=dis(A,C).
二、与01串的编辑距离为1的不同01串的个数期望值
题目描述:对于任意一个长度为n的01串,问与该串编辑距离为1的不同的01串的期望值是多少?
1.对于转换操作,我们很容易得出有n个答案。
对于删除和增加操作,我们可以知道答案应当与数据游程数有关。相邻数据两两之间不同或者相同的期望值为$ \frac {n-1} 2 $,则游程数的期望值为$ \frac {n-1} 2 $+1(初始游程)$ = \frac{n+1} 2 $.2.对于删除操作,只有操作使游程数发生变化时会产生新串,答案是$ \frac {n+1} 2 $.
3.对于增加操作,如果操作没有使得游程数增加,那么显然在01交界处的和在相同数字之间增加的串是一样的,所以答案一样是$ \frac {n+1} 2 $.
4.如果操作使得游程数增加,那么就是在包括头部前和尾部后的每一个相同点的位置都有可能加上一个不同的数字,即 $ (n+1) - \frac {n-1} 2 = \frac {n+3} 2 $
因此总的期望值为 $ E(f(X))=n+\frac{n+1}2+\frac{n+1} 2+\frac{n+3}2=\frac52(n+1)$
用以上方式分类讨论也可以得出与一个01串的编辑距离为1的01串的实际个数。
三、长度为n的01串与之编辑距离为2的等长01串的个数期望值
题目描述:给定一个长度为n(n>=2)的01串,求与之等长的编辑距离为2的01串的个数期望值。
1.对于转换操作,显然存在$C_n^2$种选择方式。
2.由于删除和增加操作会造成长度的删减,因此一定是一个删除操作和一个增加操作,我们先假设增加操作在删除操作左边(不可能在同一位置),然后将答案乘以2。
那么我们的操作就相当于选定一个长度为k的区间,将该区间的第一项删除然后全部右移一位。如果k为2,那么该操作相当于直接将两位进行替换操作,因此k一定要大于等于3.
其次,对于一个游程,删除游程中的一个数字和删除游程开头的一个数字影响是一样的,在游程中增加一个相同的数字和增加在其末尾或开头影响是一样的,因此我们删除的时候要删除区间第一第二项不同的时候才是有效删除,两项相异的概率为$\frac 12 $,而增加的时候一定要增加和末尾相异的数字。因此这部分的总和为
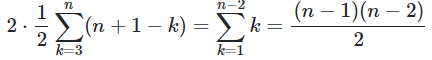
3.当我们选择的区间除了前两项以外每一项都与前一项相同,例如选择的区间为11110,最后会变为01111,相当于转换两个位置,这种情况我们要完全剔除,对于一个区间(前两项一确定互补),这种情况有
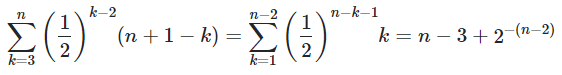
4.当我们选择的区间产生01不断交替出现的情况,此时我们左删右增或是左增右删产生的结果是一样的,因此我们只保留一个,故这种情况有是上式的1/2,
综上,最终的答案是
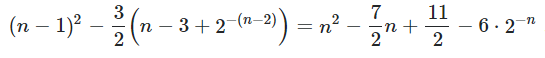



 浙公网安备 33010602011771号
浙公网安备 33010602011771号