专题整理：数论（1）

本博客包含：乘法逆元三种求法、同余方程、拓展欧几里得、欧拉定理等

一、题目链接：https://www.luogu.com.cn/problem/P3811

二、题目描述&引入概念

给定n，p(1<=n<=3*10⁶,n<p<20000528，p为质数)求1~n中所有整数在模p意义下的乘法逆元。

什么是逆元？

简单来说，就是某个数倒数，只不过这个倒数是在取模意义下的倒数，在某个模数下，某个数乘以其逆元后取模要等于1,。

用式子来表示就是ax≡1（mod p），此时x称为a在mod p意义下的乘法逆元。

举例来说，a=10，p=13.当x=4的时候，（4*10）%13=1，则称10为4在模13意义下的逆元。

显然某个a在模某个p意义下的逆元不止一个。

三、求逆元方法一----拓展欧几里得

3-1、辗转相除法（欧几里得法）求最小公倍数

基本原理是：两个数的最大公约数等于它们中较小的数和两数之差的最大公约数。因此不断通过辗转相除减小两数大小求得最大公约数（gcd）

简单证明：设k为a和b(a>b)的最大公约数，a=n1·k，b=n2·k。又a%b=a-(a/b)·b，故a%b=k·(n1-a/b*n2），它和b的最大公因数仍为k。

 

inline int gcd(int a,int b)
{
    if(0==b) return a;
    else return gcd(b,a%b);
}

3-2、同余方程

3-2-1、题目地址：https://www.luogu.com.cn/problem/P1082

题目描述：给定a和b，求关于同余方程ax≡1(mod b)的最小整数解。

可以看出此时的x就是a在%b意义下的最小逆元。

我们将ax≡1(mod b)转换一下可以得到ax+by=1,并且此时y应当是一个负数。

3-2-2、裴蜀定理

内容：若a与b是整数，且gcd(a,b)=d,则对于任意整数x,y。ax+by必定是d的倍数。特别地，一定存在x和y，使ax+by=gcd(a,b)成立。

也可以这样表述：对于不定方程ax+by=m，其有解的充要条件是m整除gcd(a,b)。

推论：a,b互质的充要条件是存在整数x,y使ax+by=1。

由此我们可以得知a和b是互质的，gcd(a,b)=1。

裴蜀定理证明

必要性的证明比较显然，由于a和b整除gcd(a,b)，故m=ax+by必定整除gcd(a,b)

充分性的证明则需要用到扩展欧几里得。

3-3、拓展欧几里得

3-3-1、简述：

用于求解ax+by=gcd(a,b)的所有整数解的一种算法。

思路首先算出一组公式的一组特解，然后推广到所有解中去。

3-3-2、如何求特解:

由辗转相除法知道gcd(a,b)=gcd(b,a%b);

ax+by=gcd(a,b)------(1)

设bx+(a%b)y=gcd(b,a%b) -----(2)。

假设有一组解x₀,y₀满足式子(2)，则有

bx₀+(a%b)y₀=gcd(b,a%b)=gcd(a,b)=ax+by又a%b=a-(a/b)·b

故bx₀+(a%b)y₀=ax+by=bx₀+(a-a/b*b)y₀=b(x₀-a/b*y₀)+ay₀

即ax+by=ay₀+b(x₀-a/b*y₀)

所以有x=y₀,y=x₀-a/by₀

当a=gcd(a,b)时，易知有一个解为x0=1,y0=0。

利用递归法就可以求得特解。

代码：

inline void exgcd(int a,int b)
{
    if(b==0){x=1;y=0;return ;}     //由于x和y是不断变化的，所以x和y被设为了全局变量 
    else
    {
        exgcd(b,a%b);
        int k;
        k=x-a/b*y;
        x=y;
        y=k;
        return ;
    }
}

通过本方法，我们可以：

1、求得该题的同余方程的一个特解，如何得到最小解思路在后面。

2、证明裴蜀定理的充分性(即当m整除gcd(a,b)时，ax+by=m有解)

证明如下：由扩展欧几里得得知ax+by=gcd(a,b)有解x0,y0。设m=k*d，易知x=k*x0,y=k*y0为方程解。

3、求得乘法逆元。

3-3-3、如何推广所有解：

先说结论：

x=x0+(b/gcd(a,b))*t

y=y0-(a/gcd(a,b))*t

推导：

ax+by=gcd(a,b)=ax0+by0

同时除以gcd(a,b)有

a/gcd(a,b)*(x-x0)=b/gcd(a,b)*(y0-y)

已知a/gcd(a,b)和b/gcd(a,b)互质

所以通过以上式子可以看出，当x0减小的时候，y0相应的应当增加

又由于x和y为整数，距离X0和y0最近的整数解就是x+b/gcd(a,b)和y0-a/gcd(a,b)

故x=x0+b/gcd(a,b)*t

y=y0-a/gcd(a,b)*t

因此，对于同余方程那题，我们得到一个特解后，假设lim=b/gcd(a,b),只需要将(x0%lim+lim)%lim可得答案

又由于题目中的gcd(a,b)=1，故lim=b,x=(x0%lim+lim)%lim。

四、求逆元方法二------费马小定理

4-1、快速幂

利用数二进制性质快速求取a^x的大小。

基本思路：二进制的每一位对应一个十进制的值，将幂次转为二进制，相当于每次将指数对半分而底数进行平方运算，然后从小往大相乘，可以将O(n)的逐个相乘的复杂度降为O(longn)。

举例：假设x=11，其二进制是1011，故可将a^x=a^{2^0}*a^{2^1}*a^{2^3}

代码：

inline int ksm(int a,int b)
{
    int ans=1,lim=a;
    while(b>0)
    {
        if(b&1) 
        {
            ans*=lim;
            ans%=p;
        }
        lim*=lim;
        lim%=p;
        b>>=1;
    }
    return ans;
 } 

4-2、费马小定理

4-2-1、简述

若a是不能被质数p整除的正整数，则有a^p-1≡1(mod p)

故a*a^p-2推知a^p-2为a的逆元。

4-2-2、证明

引论1：若a,b,c为三个整数，m为正整数，(m,c)=1则当a*c≡b*c(mod m)时，a≡b(mod p)

 引论1证明：用取模运算的性质易证，(a*b)%p=(a%p*b%p)%p。

引论2：设m为整数且m>1，b为整数且(m,b)=1若a1,a2···an为模m的一个完全剩余系，则b*a1,b*a2,b*a3···b*an亦为其完全剩余系。

剩余类：由关于模m同余的数的集合，每一个集合叫做关于模m同余的剩余系

比如模5的一个剩余系：0，3，6，9...

完全剩余系：在模n的剩余类中各取一个元素，则这n个数就构成了模n的一个完全剩余系。

比如模3的一个完全剩余系：0，1，2

引论2证明：假设存在两个数b*a1和b*a2模p同余，则由取模运算性质可知((b%p)*(a1%p))%p=((b%p)*(a2%p))%p此时易知a1≡a2(mod p),与完全剩余系的定义相违背，舍去。

费马小定理证明：

构造模p的一个完全剩余系{0,1,2,3…p-1}

则{0，a1,2a1…(p-1)*a1}亦为其剩余系故将其中的正数相乘有：

1*2*3*...*(p-1)≡a1*2a1*3a1...(p-1)*a1(mod p)

→(p-1)!≡a1^p-1*(p-1)!(mod p)

→a1^p-1≡1(mod p)

得证。

代码：

inline ll ksm(ll a,ll b)
{
    ll ans=1,lim=a;
    while(b>0)
    {
        if(b&1) 
        {
            ans*=lim;
            ans%=p;
        }
        lim*=lim;
        lim%=p;
        b>>=1;
    }
    return ans;
 } 

int main()
{
    read(n);read(p);
    for(ll i=1;i<=n;i++)
    {
        printf("%lld\n",ksm(i,p-2));   
    }
    return 0;
}

也可以使用欧拉函数和欧拉定理证明

4-3、欧拉函数&欧拉定理

4-3-1、欧拉函数

欧拉函数φ(x)表示小于等于n中与n互质的数的数目(故有φ(1)=1)

欧拉函数通式：

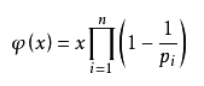
通式推导：

假设x为质数p的k次幂

φ(x)=p^k-p^k-1=(p-1)*p^k-1

由分解质因数可知n=p1^a1*p2^a2*p3^a3...pk^ak

由乘法定理有φ(n)=∏(pi-1)*p^api-1=n*∏(1-1/pi)

4-3-2、性质：

欧拉函数是不完全积性函数

积性函数：若a,b互质且f(ab)=f(a)*f(b),则f(x)是积性函数

完全积性函数：若a,b不互质且也有f(ab)=f(a)*f(b),则f(x)是完全积性函数

例如φ(12)=φ(2²*3¹)=φ(2²)*φ(3¹)=4

4-3-3、欧拉定理

内容：若a、n(n>2)为互质正整数，则有a^φ(n)≡1(mod n)

证明(和费马小定理证明方法相似)：

1、设x1,x2...xn为小于n的与n互质的数字，ax1ax2...axn对n取模后模数互不相同且获得的集合是x1,x2...xn

举例：4有1,3，若a为3，则3,9对4取模后为3,1。

证明方法与4-2-2的引论2的证明方法一致。

故x1*x2*...*xn≡ax1*ax2*...*axn(mod n)

→a^φ(n)≡1(mod n)

费马小定理就是当欧拉定理中的n为质数时的特殊形式。

五、求逆元方法三——线性算法

5-1、优化

费马小定理简便，拓展欧几里得算法通用，但是它们都有一个缺点，那就是耗时过多，对于这题的数据上限来说肯定是要超时的，我们考虑推导O(n)的线性算法

设p=k*i+r(1<r<i<p) (即k=p/i,r=p%i)

k*i+r≡0(mod p)

同时乘以i^-1和r^-1则

k*r^-1+i^-1≡0(mod p)

→i^-1≡-k*r^-1(mod p)

→i^-1≡-[p/i]*(p%i)^-1(mod p)

5-2、代码

int main()
{
    read(n);read(p);
    inv[1]=1;
    for(int i=2;i<p;i++) inv[i]=(p-p/i)*inv[p%i]%p;
    for(int i=1;i<=n;i++) printf("%lld\n",inv[i]);
    return 0;
}