SUMS
8.14
T1
简单贪心,照着题意模拟即可。
T2
给一棵树,有点权与边权,定义一棵子树 \(f(x)\) 为子树里权值为 \(x\) 的点两两距离和,并给定 \(k_i\),求以 \(i\) 为根的子树里满足 \(f(x)\) 最大的 \(x\) 与 \(i\) 的子树里编号 \(k_i\) 小的 \(y\) 的 \(f(y)\)。
那么借助转移数组,用 $ g(x,i) $ 去表示我们 \(i\) 子树的所有权值为 \(x\) 的点到点 \(i\) 的距离和,而 $ h(x,i) $ 为 \(i\) 子树里权值为 \(x\) 的点的数目。
随便搞个数据结构去维护所有出现过的权值的 \(f,h,g\) 三个数组,自底向上地启发式合并。那么就只需要考虑如何用点 \(v\) 去更新父节点 \(u\) 的信息。
我们记录 $ f'(x,u) $ 为 \(v\) 并入之前的 $ f(x,u) , g',h' $ 同理。
就会有
直接查询就行。
T3
萌萌结论题,不能被 \(ax+by\) 表示的数有 $ \frac{(a-b)(b-1)}{2} $ 个,并且最大不能被表示的数为 $ a*b-a-b $,然后用枚举的思想去找接近的项即可。
8.15
T1
牛逼的多项式,给你一个 \(n\) 维的多维体去在表面刷漆求表面被刷了 \(i\) 层漆的块分别有几个。也就是三维的一个立方体表面刷一层色,求刷了 \(i\) 层色的立方体的个数的高维度版本。
这里给出每一维度的边长 \(a_i\)。
那么分类讨论, \(a_i=1\),所有的小锥体都只会增加染色面,两个面变为了锥体。
而 $a_i \ge 2 $ 时,会发现只有两边的小锥体会增加一个染色面,中间的虽然也会增加两个面但是并不会染色,所以染色面不变。
可以分别得到式子 \(x^2\),\(2x+(a_i-2)\)
NTT就行。
T2
李超树简单题,开值域树然后直接覆盖就行。
注意操作不均衡,我们用分块去优化一下即可。
也就是对于单点修改直接插入李超树,而区间修改用分块维护,便于操作。
T3
神仙期望,题意难懂,咕咕咕
9.1
T1
给你 \(n\) 个人围成圈,每个人手里分别 \(a_i\) 个球,每个人可以选择手里 $ 0-a[i]$ 个球传递向右手边的那个人,把每个可能产生的新序列设为 \(S\),求 \(\sum\Pi a_i\),对\(998244353\)取模。
也就是对于每一种可能的序列求所有球个数的乘积再加起来。
那么就去分析性质,首先每个人给的球数量不同不代表最后序列不同。
如果每个人都会至少给出一个球,就可以让每个人都少给出相同的个数,效果也就会相同。所以至少会有一个人不传球,才会产生新的方案。
那么可以得到暴力DP式子 $ f(i,j) $ 表示第\(i\)个人给\(j\)个球的前缀乘积和,然后为了不重不漏,我们指定\(i\)是不给球的那个,并且指定他前面的人都必须给球。
最后答案是把所有的 \(f(i,0)\) 加起来。
考虑优化
那么求出来两项就可以完成转移,但是还是不能接受。
接着设 $ w(j)=\sum\limits_{l=0}^{a_j}f(j,l) $, $ g(j)=\sum\limits_{l=0}^{a_j}f(j,l)\times l,h_1(x)=\frac{(1+x)\times x}{2},h_2=\frac{x\times(x+1)\times(2x+1)}{6} $
可得到
所以我们只需要累加 $ a_jw(i-1)+g(i-1) $,矩阵维护一下即可达到 \(o(n)\) 级别。
#define int long long
#define ll long long
#define Maxn 100010
const ll p = 998244353;
inline ll qp(int a, int b)
{
ll res = 1;
while (b)
{
if (b & 1)
res = 1ll * res * a % p;
a = 1ll * a * a % p;
b >>= 1;
}
return res;
}
const ll inv2 = qp(2, p - 2), inv6 = qp(6, p - 2);
int n;
ll a[Maxn], f[Maxn][2];
inline ll sum(ll x)
{
return x * (x + 1) % p * inv2 % p;
}
inline ll psum(ll x)
{
return x * (x + 1) % p * (x * 2 + 1) % p * inv6 % p;
}
inline int sol(int x, int o)
{
memset(f, 0, sizeof(f));
f[1][o]=1;
for (int i = 1; i <= n; i++)
{
f[i + 1][0] = (f[i + 1][0] + (sum(a[i] - x) * f[i][0] % p)) % p;
f[i + 1][1] = (f[i + 1][1] + (a[i] * sum(a[i]) % p - psum(a[i]) + p) % p * f[i][0] % p) % p;
f[i + 1][0] = (f[i + 1][0] + (a[i] + 1 - x) * f[i][1] % p) % p;
f[i + 1][1] = (f[i + 1][1] + (sum(a[i]) * f[i][1] % p)) % p;
}
return f[n + 1][o];
}
inline void work()
{
n = read();
for (int i = 1; i <= n; i++)
a[i] = read();
write(((sol(0, 0) + sol(0, 1)) % p - (sol(1, 0) + sol(1, 1)) % p + p) % p);
return dwd;
}
signed main()
{
work();
return 0;
}
T2
CF1470E。

T3
一个集合的装饰子集为不被其他任何数包含的子集, \(a\) 包含 \(b\) 当且仅当二进制下 \(b\) 为 \(1\) 的位上 \(a\) 也为 \(1\)。
那么考虑一下原序列的装饰子集 \(S\),并且设 \(x\in S\)。那么 \(x\) 不被任何数包含,也就是说对于任意子串同样是不会被包含。所以 \(x\) 肯定是属于某个子集的装饰子集。
那么也就是说所有子串装饰子集等于 \(S\)。
我们用 \(l_i\) 表示让 \([l_i,i]\) 包含所有的 \(S\) 内元素的最大 \(l_i\) ,双指针求出即可。
直接DP, \(f_i\) 就表示 $ [1,i] $ 的答案,初始化为0。那么对于一个可能的 \(l_i\),有 $ f(i)=\sum\limits_{j=0}^{l_i-1}f(j) $,也就表示了 \([j,i]\) 为合法子串。可以前缀和优化到 $O(n) $。
对于 \(S\),直接求就行。
#define int long long
#define Maxn 3000010
const int p = 1e9 + 7;
const int Maxv = 1 << 21;
int n, cnt, sum;
int ansx;
int a[Maxn], sums[Maxn], t[Maxv];
int f[Maxn], T[Maxv], vis[Maxv];
inline void work()
{
n = read();
for (int i = 1; i <= n; i++)
a[i] = read(), t[a[i]] = vis[a[i]] = 1;
for (int LEN = 2; LEN <= Maxv; LEN <<= 1)
for (int i = 0, k = LEN / 2; i < (Maxv); i += LEN)
for (int j = 0; j < k; j++)
t[i + j] += t[i + j + k];
for (int i = 0; i < Maxv; i++)
vis[i] &= (t[i] == 1), sum += vis[i];
f[0] = sums[0] = 1;
for (int j = 1, i = 1; i <= n; i++)
{
if (vis[a[i]])
cnt += (T[a[i]] == 0), T[a[i]]++;
while (cnt == sum and (vis[a[j]] == 0 or T[a[j]] > 1))
{
if (vis[a[j]])
T[a[j]]--;
j++;
}
if (cnt == sum)
f[i] = sums[j - 1];
sums[i] = (sums[i - 1] + f[i]) % p;
}
write(f[n]);
return dwd;
}
signed main()
{
work();
return 0;
}
9.2
T1
模拟。
T2
就是一个必须经过P个点的最短路问题。比较暴力的一种方式是BFS,每次都去枚举下一步搜索哪个点,但是一大问题是搜索考虑了顺序问题,因此会有大量的无意义的搜索树,而我们只关心是否P个点全都经过。观察到P很小,所以采用状压的方法去表示还未经过的点,然后去更新。
那么设 $ dis[x][y][s] $ 来表示还没去过 \(s\) 集合中的点,并且当前坐标在 \((x,y)\) 的最短距离。
直接BFS更新。
又发现 $ dis[x][y][s] $ 的三维中 \(s\) 在很多点用不到,那么就会有浪费。
所以直接在P个点定义 $ dis[i][s] $,在第 \(i\) 个点时的最短路。转移的时候利用两个点的最短路即可。
关于体积问题,在每个点都会重新膨胀,那么其实在每个点的最大膨胀值是可以处理出来的,直接在BFS过程中加入答案一起统计即可。
9.3
T1
组合数,树转化为序列,那么组合就是子序列。所以对于每一个子序列,都定义其最大值为最大值里位置最靠后的。那么我们就需要枚举这个最大值,看看有多少个子序列的最大值是它,也就是转化为每个点的贡献。
那么我们就需要去满足子序列在这个位置左边的,数字不会超过这个位置上的数,在位置右侧的子序列,数字都小于这个位置上的数字(最靠后)。
若我们一共找出有 $ m $ 个这种数字,那么 $ C_m^{K-1} $ 就是这种序列的个数。
怎么找这种数字?考虑把序列按照值为第一关键字,位置为第二关键字去从小到大排序。之后就发现对于每个位置,如果它的排名是 $ p-1 $,那么数字的总数就是 \(p-1\) 。
那么扫一遍就可以统计出答案了。
T2
发现按照题目要求的话最终一定会回到起点。
那么我们考虑去从最终到达的特定位置向单一方向出发,那么设辅助数组 \(F(x,y)\) 去表示单次出行离开最终的位置 \(x\) 的时间时你距离最终位置距离为 \(y\) 的方案数。
那么有 $ F(1,1)=1,F(x,y)=F(x-1,y-1)+F(x-1,y+1) $。
那么就有递推式子,用矩阵乘法优化即可通过。
T3
对于等差数列的二进制下,会有第 \(i\) 项与第 \(2^K+i\) 项在 \(K\) 位上的数字相同。
然后原数列就会有循环节,拆出来就行。
9.5
T1
先转化一下 \(i|j==k\) ,那么答案就是前缀最大。
那么就直接去考虑每个 \(K\) 怎么求答案,发现可以直接枚举子集。
但是直接枚举显然不行,那么我们去借助高位前缀和。
造一个结构体去捆绑一下每一个 \(K\) 代表的最大值和次大值,那么初始的时候最大值为当前值,次大值为0.然后高位前缀和,但是这里的“前缀和”所代表的时所有前缀的最大值。
T2
题目要求把两个连续的1或者0去进行操作,我们发现会不可避免地去选择它是属于前面还是后面,那么我们就去把下标为偶数的位置全部取反,记我们操作之后地字符串为 \(s',t'\)。那么不难发现,我们把元字符两个相邻并且相同的位置取反之后,等价于在新的字符串上交换这两个字符。
那么也就是说转化为,交换 \(s'\) 里两个相邻的字符,至少需要多少次操作才能把一个字符串变成另一个字符串。
那么显然如果有解的话肯定是两个字符串里相同的字符出现的次数相同。那么我们去考虑怎么计算次数。
如果对于一般的序列,我们通常去计算逆序对来解决问题,但是对于这种特殊的01序列我们会有一个更简单的方法。
设我们 \(s'\) 里第 \(i\) 个 \(1\) 的下标为 \(x_i\), \(t'\) 里第 \(i\) 个 \(1\) 下标为 \(y_i\),那么最小的交换次数就是 $ \sum\limits_{i=1}^{c} |x_i-y_i| $。
但是还是很麻烦,我们去接着化简。有一个套路的方法 \(a_i\) 为 \(s'\) 前 \(i\) 个里 \(1\) 的出现次数, \(b_i\) 同理,那么答案就是 $ \sum\limits_{i=1}^{c} |a_i-b_i| $。
因为每次交换两个数的时候,最多只会让一个前缀和发生变化。
有了结论之后就很简单了,直接蒜就行。
记 $ pre(i,j) $ 为前 \(i\) 个数让 $ a_i-b_i=j $ 的方案数,$ suf(i,j) $ 表示对应的后缀的方案数,那么贡献就是 $ pre(i,j) \times suf(i+1,-j) \times |j| $。
T3
就是每次可以更改一个位置上的数,希望让有特定位置关系的极差变小,求最小操作数。
我们去按照前缀最小值把序列分段,发现每段时互不影响的。
那么对于每一段我们也需要去考虑最小值和最大值 \(x,y\)。如果 $ y-x==f(a) $,那么我们必须去选择一个位置 \(i\),把它之前的 \(x\) 和它之后的 \(y\) 全部删掉,最终也就是求最小值。
直接前后缀和做就行。
9.6
T1
求出一个排列并且有形如 $ (a,b) $ 限制条件表示 $ a $ 必须在 $ b $ 之前,最大化它的子段和。
那么我们考虑枚举这个最大的子段和包含了哪些数,一个方案合法的充要条件是要满足下面的限制:
若存在 \(i->j->k\) 的路径,若选择 \(i,k\) ,则必选 \(j\)。
这等价于对每一条路径的点都可以分成“不选->选->不选”的形式。
我们把每个点都拆成 $ S->i_1->i_2->T,然后割三条边分别表示在某一段中,那么每个限制就是限制 \(a\) 的段小于等于 \(b\) 的段,直接把 $ (a_1,b_1),(a_2,b_2) $ 连上正无穷的边即可。
s
也就是先把权值为正的所有数都放在一起,但是全选的话也就代表着需要选很多负的,所以我们考虑直接把其中一些点扔走(左右),或者直接选上的负点来让左右两边的段都变大。
所以直接跑最小割,正值之和减去最小割即可。
T2
Latex太多了,不打了
原题:ARC127F
T3
这种异或的题一般都放到01Tire上,这题也不例外。
我们去直接设 $ f(u,v) $ 表示从 \(u,v\) 的子树中选一些数,使得凉凉异或不大于 \(X\) 的方案数。
那么答案就是 $ f(1,1) $
如果 X 当前位是0,那么 $ f(u,v)=f(ls_u,ls_v)+f(rs_u,rs_v)−1 $,减 \(1\) 是为了减掉出现两次的空集,如果 \(u≠v\),也就是更高位出现了\(1\),如果现在只在一颗子树中选相当于撤回了更高位的\(1\),就不需要考虑这一位了,补上对应的方案。
如果 \(X\) 当前位是\(1\),如果 \(u=v,f(u,u)=f(ls_u,rs_u)\),如果 \(u≠v\),发现 $f(ls_u,rs_v) $ 与 $ f(rs_u,ls_v) $ 相互独立,也就是 \(f(u,v)=f(ls_u,rs_v)×f(rs_u,ls_v)\)。
DP即可。
9.8
T1
树形DP+容斥。
我们定义 \(g_i\) 去表示 \(i\) 个点两两配对的方案数,若是奇数则为 \(0\),偶数就是小于 \(i\) 的拘束的积。
那么我们接着设 \(f_{i,j}\) 表示 \(i\) 的子树里,包含 \(i\) 的连通块大小为 \(j\) 的方案数,并且设 $ f_{i,0} $ 为 \(i\) 的子树内全部匹配的方案数。
大概就像树形背包一样转移。
我们对于 \(f_{i,0}\) 的转移,需要加上一个 \(-1\) 的系数,原因是它上面还有一条边链向父亲,需要割掉,集合大小 \(+1\),并且其转移为 $ f_{i,0}=-\sum\limits_{j=0}^{siz} f_{i,j}\times g_j $。
最后对于根的集合大小则不用 \(+1\),直接输出 \(-f{1,0}\)。
T2
无解情况显然可以判定,我们考虑怎么去用最小的花费转移为回文串。
我们发现对于每种字符,他总是首尾匹配的。更具体地说,我们直接从前往后扫,如果扫到一个没有匹配上的,我们就将这种字符的最后一个同种字符与他相匹配即可。也就是说如果这个字符位置为 \(i\),与之匹配的位置就是 \(n-i+1\)。
可以验证这种交换方式是最优的。
所以直接求逆序对就行。
T3
阴间题,大体来说就是维护两个栈,同时碰到首尾相同的字符就消掉,看能不能消完即可。因为是贺的,所以不再阐述。
9.9
T1
区间LCM,想一想LCM的性质,本质就是把两个数质因子分解,然后每个因子的次数取个最大值。
考虑根号分治,先想因子小于等于 \(\sqrt{a}\) 的情况:
发现对于值域内不会超过\(86\)个质因子,那么就是对于每个因子次数区间求最大值,直接线段树。
对于另一种情况,我们发现这么大的质因子对于每个 \(a_i\) 只可能有一个,如果有就直接单独处理即可。对于不含有此因子的数,视为 \(1\)。
那么就是询问区间内所有不同的大质数的乘积。
我们和区间统计数字种类相似的,预处理一个 \(pre\) 数组去表示每个大质数数上次出现的位置,然后询问就变成了区间里 \(pre\) 小于等于询问左端点的所有 \(a_i\) 中大质数的乘积。
那么直接用主席树维护,每个位置 \(i\) 都用一棵线段树去维护 \(1-i\) 内 \(pre\) 在一段区间内的大质数乘积即可。
最后别忘了乘上就行。
T2
神必的期望。
考虑枚举第一格的数,那么我们需要知道 \(f[i][j]\) 表示长度限制为 \(i\),结束时第一格为 \(j\) 的概率,\(g[i][j]\) 表示此时答案的期望。
求 \(f\) 和 \(g\) 时需要知道 \(x[i][j]\) 表示长度限制为 \(i\),第一格弄出 \(j\) 的概率,以及 \(u[i][j]\) 表示长度限制为 \(i\),初始时第一格为 \(j\) 的期望答案。
具体转移方程可以参考标程。
写出转移方程后不难发现将 \(g[i][j]\) 改为长度限制为 \(i\),初始时第一格为 \(j\),结束时第一格还是 \(j\) 的概率*期望,就可以不用记 \(f[i][j]\),同时转移方程会简化很多,
复杂度还会少个 \(log(\)模数\()\)。
时间复杂度 \(O(nm)\)。
#include <cstdio>
#include <iostream>
using namespace std;
typedef long long ll;
const int P = 1e9 + 7;
const int N = 2005;
int n, m, t;
ll g[N];
ll f[N][N];
ll p[N][N];
ll q[N][N];
ll qpow(ll a, ll b);
int main()
{
cin >> n >> m >> t;
int maxn = min(t, n + m - 1);
ll invm = qpow(m, P - 2);
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= maxn; j++)
{
p[i][j] = p[i][j - 1] * p[i - 1][j - 1] % P;
if (j <= m)
(p[i][j] += invm) %= P;
q[i][j] = 1;
if (j != maxn)
q[i][j] = (q[i][j] - p[i - 1][j] + P) % P;
}
for (int j = maxn; j >= 1; j--)
{
ll tmp = (q[i][j] * j % P + g[i - 1]) % P;
if (j != maxn)
tmp = (tmp - p[i - 1][j] * f[i - 1][j] % P + P) % P;
f[i][j] = tmp;
if (j != maxn)
(f[i][j] += (1 - q[i][j] + P) * f[i][j + 1] % P) %= P;
(g[i] += p[i][j] * tmp % P) %= P;
}
}
cout << g[n];
}
ll qpow(ll a, ll b)
{
ll ans = 1;
a %= P;
for (; b; b >>= 1, a = a * a % P)
if (b & 1)
ans = ans * a % P;
return ans;
}
T3
若可以变成回文串,则至多有一种字母出现了奇数次。
那么我们考虑状压,二进制一位代表一个字母,那么整个路径的疑惑和要么是0要么是 \(2^x\)。
那么我们设 $ f(x) $ 表示 \(x\) 到根节点的异或和,然后 $ f(u) xor f(v) $ 为 \(0\) 或者 \(2^k\) 时,代表 \((u,v)\) 是一条合法路径。
那么每个点先从子树继承答案,然后开桶,子树之间计算贡献。
重儿子的话就直接继承即可。
9.12
T1
把这个需要统计的东西莫反一下,变为 \(k|gcd\) 的数量。那么我们对于每个边权都只保留质因子是否存在即可,那么每个数的质因子都不会超过 \(7\) 个。对于每一个 \(k\),把边权是 \(k\) 的倍数的边都取出来,然后用并查集统计答案。对于我们修改涉及到的边,开始并不加入并查集,然后枚举时间轴时再逐一将其加入,统计答案,再删除即可。
T2
我们定义一下 \(w\) 为前缀异或,即为 \(w_k=0 \ \oplus \ 1 \ \oplus...(k-1)\),那么我们就可以把问题转化为寻找数对满足 \(0 \le i < A,0\le j<B,w_i\oplus w_j=V\)。
那么对于 \(w\),有一个经典结论: $ w_{4x}=4x,w_{4x+1}=1,w_{4x+2}=4x+3,w_{4x+3}=0 $
那么发现只需要确定了 \(i,j\) 模 \(4\) 的余数所有可能的情况即可。
直接把 \(V/4\) 和 \(V\mod 4\) 分开算,分别取枚举 \(l\mod 4,r\mod 4\)。计算有多少个 \(l/4,r/4\)异或和为 \(V/4\),寄搜就行。
T3
看到这种条件计数题,可以思考一下什么样的图形符合条件。
画一画图发现,不可能有 \(\le 3\) 个黄色的分开部分,否则就会有一行多个蓝色块。
并且不可能黄色全连通并且蓝色也全连通。
假设现在统计黄色的两个部分分开的方案数,这时候就需要多画图,找出符合条件的情况。
情况如下,这是左边黄色块在右边黄色块下面的情况。也可以在上面,只要把答案乘上 2 。
如何计算个数?
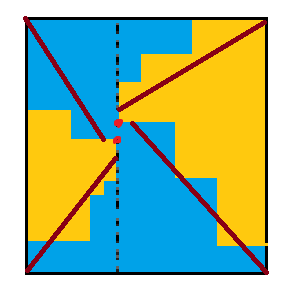
考虑枚举中间那条虚线的位置,再枚举 2 个红点的位置,计算符合条件的黄色块边界数量。
这个可以通过 4 个角到某几个点的路线方案数乘起来计算,路径方案数显然是组合数。
见下图:(由于枚举的是右上角,左下角,所以最后一步的方向是确定的。)
然后前缀和优化即可。
还要计算蓝色两块分开的方案数,直接交换 \(n,m\) 算就行了。
然后就会发现算重了,蓝色、黄色都分开的重复算了。
其实很好处理,在算蓝色的时候强制让两个红点相差 \(\ge 1\) 即可。
有一点点细节,画画图就会了。
9.13
T1
你在 \(A\) 上建棵主席树,每个点都去储存到根节点路径上的信息。
然后求出来每个点在 \(B\) 树上的DFS序,在 \(A\) 树上建主席树的时候把每个点在 \(B\) 树上的子树对应区间去进行一个最大值的覆盖的做。
然后询问就成了询问点的最大值。
T2

T3
神必的数数题。
把他放在二维的坐标系上,\(x,y\)轴分别表示它往左走和往右走的步数,每个机器人的坐标就分别表示了它需要走的步数,那么一个机器人在何时溜走就看他是先过 \(x\) 轴上的界限还是 \(y\) 轴了。
那么若一个机器人的坐标定义为 \((a_i-0.5,b_i-0.5)\),所有在曲线左上方的都会从左侧的出口溜走,右下方的反之。
那么对于每一个从右侧出口溜走的机器人集合,就可以构造出一个唯一的与之相对应的折线。
方案数显然就是这种直线的个数。令 \(f_i\) 去表示延伸到 \(i\) 的机器人,并且这是个机器人,那么转移方程就是 $ f_i=\sum\limits_{a_j<a_i,b_j<b_i}f_{j+1} $。
那么借助树状数组去数点,优化到 \(O(nlogn)\)。
9.14
T1
区间出现概率严格大于 \(p\) 的数,由于题目给出的限制较为宽松,只要包含即可,那么我们就直接用摩尔投票在多人情况下的拓展即可解决,剩下的就是普通的线段树维护了。
摩尔投票:找区间绝对众数的方法,具体方法是一个一个去抵消,可以理解为粉丝给爱豆投票,两个粉丝发生冲突的时候会互相把对面打残了然后就不能参加投票了。
T2
CTSC题,牛的一比。
我们先直接去考虑暴力做法。发现一种方法是我们把 SAM 建出来,然后 \(O(n)\) 去枚举起点,\(O(n)\) 去 dfs ,不断拓展 v,那么就可以边 dfs 边在 SAM 上匹配字符串,最终复杂度 \(O(n^2)\)。
考虑另外一种暴力做法,我们发现每一对 \(u,v\) 都会有一个 LCA,并且可能会有很多对不同的点对 LCA 相同,那么我们考虑一个 LCA 可以对它所“管辖”的点对造成多少贡献。
我们不妨定义 $ F(x)=\sum\limits_{x\in k的子树}\sum\limits_{y\in k的子树}Occur(Path(x,k)+Path(k,y)) $ ,那么我们所
求的以 \(k\) 为根的子树的答案就是
$ F(k)-\sum\limits_{x\in k的直接孩子}F(x) $,也就是所有链对的出现次数和减去最近公共祖先不在Z的所有链对的出现次数和。
函数 \(F\) 的计算可以使用我们刚才讨论的方法。 我们建立母串S的后缀树和母串 S 的逆序串 Srev 的后缀树,然后从 \(k\) 结点出发 DFS 一遍,记录下各个结点在两棵后缀树上对应到达的位置。 然后对两棵后缀树均 DFS 一遍,把标记推下去到叶子结点(对应着匹配的后缀在串中位置,从而得到串中的每个位置开始各能匹配多少个 \(k\) 出发的串,然后把对应位置的匹配数目相乘并求和,即可求出 \(F(k)\) 的值。
那么我们发现这个朴素算法可以改进一下,算法中的 \(n^2\) 实际上是各个子树的大小之和。但是这是一棵无根树对吧,所以我们考虑淀粉质去选取树的中心作为根节点来分治,可以把复杂度优化到 $ O(NlogN+MN) $。
有了上面点分治的改进后,我们发现,时间复杂度的瓶颈已经变成了每次 DFS 后缀树
的 $ O(M) $。 而这个复杂度难以优化。我们发现,计算 \(ans(k)\) 的复杂度不管 \(k\) 的子树有多大都
始终是 $ O(M) $,这对于较小的子树显然很浪费。 而朴素算法晁的复杂度正好是与 \(M\) 无关的,始终是子树大小的平方。于是我们产生了一个想法,如果分治得到的子树足够小了,就不妨把任务交给第一种朴素算法来做,这样显然比用朴素算法划算很多。
我们不妨假设当子树大小不超过某个值 \(S\) 时我们将使用第一个朴素算法。因为我们选取重心作为根结点进行点分治,所以我们可以保证,每次分治得到的最大子树大小不会超过原子树大小的一半。复杂度可以得到保证(O(能过))。
9.16
T1

T2

T3
首先我们使用 01Trie 上二分的方式来求出“第K大”,令求出来的为 kth
当然这一步也可以直接二分 \(O(nlog^2n)\),但是可以做到 \(O(nlogn)\)。
然后我们需要求出所有“大于第k大”的异或和的和
怎么做呢?
我们贪心地从大到小考虑 kth 的每一位,如果发现某一位为 \(0\),那就说明有空隙
我们就得把所有异或和中 "这一位为\(1\)" 的数求个和,然后累加到答案。
这玩意我们可以预处理处 \(cnt[x][y]\) 表示 以 \(x\) 为根的子树中有多少个数有 \(y\) 这一位,然后每次要求和的时候拆位,一位一位累加,可以做到 \(O(nlog^2n)\) 的复杂度。
别忘了long long。
9.20
T1
怪题,看到数据范围我啪的一下就是一个表啊,很快啊
直接DP转移打表即可。

T2
这玩意一看就一眼不可做。。。
我们先把和转化为期望,然后最后再乘上方案数即可。
由于Latex不好打,我们这里直接放图片。


T3
显然我们移动肯定是比不动要更快的,所以直接考虑怎么移动。
那么这个操作的本质就是给原序列分为很多小组,并且认为划定一个峰点,峰点左侧向右走,右侧向左走,最后双向奔赴。
那么每个点都会由两种状态构成,要么先向左匹配之后再回头匹配,要么就是先向右匹配。
所以我们定义一下如果 $ p_i $ 行为 \(2\) 而 $ p_{i+1} $ 行为 \(1\),那么 \(i,i+1\) 均为匹配状态。
那么有一个结论:最优解中是不存在连续两个不匹配的点的。
所以我们直接强制让 \(f_i\) 为匹配 \(i,i-1\),dp即可。
9.22
T1
注意到了 $ |a_i -b_i|\le 12 $,可以状压连通块了。
看上去状态很多,实际上因为它图本身限制,你在跑的时候判断一下连通性的话就可以省掉很多的无用状态,
所以实际上跑的飞快。。。
然后状压就行。
T2
ARC135F
T3
如果把所有可能的最终集合排序并且找到字典序(我也不知道怎么表述了……)最大的。显然就是在第 \(i\) 次插入时插入 \(i\) 可以使得字典序最大。
那么,如果一种集合的字典序大于这个最大的字典序,那肯定无法构造。反之则必定可以构造,下面是一种方案
把所有出现在最终集合中的数从小到大插入,如果碰到操作2就插一个不在最终集合内的数垫背。
最后再写一个 \(O(n^2)\) dp,就很简单了。
9.23
T1
给定 \(1 \dots N\) 的一个排列 \(a\),共有 \(M\) 次操作,包含两种:
1 l m r表示将区间 \([l,r]\) 内的元素修改为 \(merge(\lbrace a_l,\ a_l+1,\ \dots,a_m \rbrace, \lbrace a_{m+1},\ a_{m+2},\ \dots,\ a_r)\)。2 x表示询问 \(a_x\) 的值。其中
merge(a,b)表示归并操作,代码如下:def merge(a,b): c=[] while a.size() and b.size(): if a[0]<b[0]: c.append(a[0]) a.pop_front() else: c.append(b[0]) b.pop_front() return c+a+b\(N,\ M \leq 10^5,\ 1=l \leq m < r \leq N,\ 1 \leq i \leq N\)。
对于每一组 \(1\) 操作,我们先考虑区间 \([m+1,r]\) 内的元素最终的位置在哪。不妨设 \(f(i)\) 为区间 \([l,i]\) 的最大值,\(g(i)\) 为区间 \([m+1,i]\) 的最大值,那么右区间的一个元素 \(a_i\),经过一轮 merge操作后的位置就是 \(k+i-m\),其中 \(k\) 为满足 \(f(k)<g(i)\) 的最大值。
形象地说,在每一次 merge 操作结束后,区间 \([m+1,r]\) 的每一个元素最终所处的位置将区间 \([l,r]\) 划分为了若干小段,每个小段都是原区间 \([l,m]\) 的一段连续子区间。显然上文所说的 \(k\) 可以通过二分在 \(O(\log n)\) 的时间内得到,我们需要做的就是维护一个支持区间分裂合并的数据结构,这里使用 \(Fhq-treap\) 实现。
利用上述方法,发现左区间同样对右区间产生着相同的贡献,相应的维护即可。这样的时间复杂度是均摊的,不会理性证明,但是可以这样感性理解:设 \(P_i\) 为第 \(i\) 次操作后整个排列 \(a\) 的前缀最大值所构成的序列,显然 \(P_i\) 的字典序是单调不上升的,而当某一次操作导致 \(P\) 的字典序最小后,整个序列变为有序,此时进行 \(1\) 操作的时间复杂度为 \(O(1)\) ,而在这个时刻之前的修改操作所花费的时间也在随着 \(P_i\) 字典序的变小而降低,根据实际表现,最终大概会均摊至 \(O(n \log^2 n)\) 左右的复杂度。
T2
给出一个序列 \(\lbrace 1,\ 2,\dots,\ n \rbrace\),可以对它进行 \(m\) 次以下操作:
- 删除任意一个数,将它加到这个序列的开头或者末尾。
最后你需要得到序列 \(\lbrace a_i \rbrace\),其中 \(a_i\) 同样是 \(1-n\) 的一个排列。求合法的方案数模 \(998244353\)。
两种操作方案相同当且仅当每次操作都选择了相同的元素,移动到了相同的方向。
\(2 \leq n \leq 3000,\ 1 \leq m \leq 3000\)。
首先注意到,对于一个数,只有最后一次操作有意义。
那么对于每个数只保留最后一次操作,称其为简化操作序列,假设长度为 \(k\)。那么出去简化操作之外的其它操作的方案数就是: \(\dbinom{m}{k} \times 2^{m-k}\)。
接下来考虑简化操作序列的方案数。发现如果把序列 \(1-n\) 中的一些数抽出去,那么中间剩下的就是一段递增的数列。在 \(a\) 中枚举这个递增区间 \([l,r]\),那么 $a_{1},\ a_{2},\dots a_{l-1} $的最后一次操作就是向左的,而 $ a_{r+1} \dots a_{n} $ 就是向右的。
那么我们已经把操作方向确定,并且向左的操作之间的顺序也已经确定,但是左右操作之间的交换顺序还是任意的,可以随便排列。
随意这部分的方案数 $ \dbinom{l-1+n-r}{l-1} $。
那么答案就是 $ \sum\limits_{k=0}{n}f(k)\dbinom{m}{k}2 $。
其中 $ f(k) $ 表示长度为 \(k\) 的合法简化操作序列数量。
T3
在一个长度为 \(n\) 的序列里面挑 \(m\) 个数使得挑出来的数在原序列里面不相邻,对每一种合法方案都求出这个序列的 \(sum\),求所有合法方案的 \(sum\) 和对 \(998244353\) 取模。
一道F题。
我们先定义一下 $ ring(n,k) $ 在一个长度为 \(n\) 的环里面选取 \(k\) 个的方案数,而 $ line(n,k) $ 表示在一个长度为 \(n\) 数组里取 \(k\) 个的方案数。
那么我们由插板法可得 $ line(n,k)=\dbinom{n-k+1}{k} $, $ ring(n,k)=line(n-1,k)\times$ 第一个元素不取 $ +line(n-3,k-1)\times $ 第一个元素取,所以都是可以直接求的。
那么就把原题转化为一个数可以在多少个满足条件的序列里存在,乘起来再加上就是答案。
那么我们发现为环时, $ cnt_i=\frac{ring(n,k)\times k}{n} $。
为序列时,只多了 \(a_1,a_n\) 都可以取到的情况,那么就可以直接递归了。
最终复杂度 \(O(n)\)。
当然这题还有个EX,具体就是把不能选连续的 \(2\) 个原序列元素改为了不能选连续的 \(d\) 个,感兴趣的可以思考一下我不会。
9.26
T1
大体来说就是在 $ n*m $ 的街道上走路,然后水平方向上移动的代价都相同,在竖直方向上每条路的代价都相互独立,各自给出,求从 \((0,0)\) 的起点到任意 $ (i,j) $ 的终点最短路之和。
那么发现走最短路无非是两种情况(如图)
那么可以发现从编号小的列走向编号大的列的情况下横向移动的花费是固定的(显然可利用平移线段证明)
那么求 \(t_i\) 时就可以直接求成其前缀最小值,并不影响答案。
那么最后一列的每个位置的最短路都是和这个位置的行有关的一个一次函数(变量是横向移动,竖向移动的时候我们强制设置它是走我们选中的这条竖线)。
那么走到后面再走回来的时候也就相当于了加上一个相同的贡献。
所以本质上我们就是维护了一堆一次函数,我们分别从其中选取几段构成一个凸包的上凸壳即可保证最终花费为最少的。
那么发现当列变大时,一次函数斜率不会增加,所以斜率优化DP即可解决。
T2
就是维护一个区间乘,单点除,区间和,同时模数任意。
那么瓶颈就在于除操作。
乘一下发现 \(p\le 1e9+10\),所以 \(P\) 里面不会超过 \(9\) 个不同的质因子。
所以考虑对于 \(P\) 进行分解,然后进行除法的时候我们把除数也分解,分解为一部分是与 \(P\) 的质因子有重叠部分的,另一部分与 \(P\) 互质。
第一部分在处理的时候直接进行次数的加减即可,第二部分由于是互质,所以我们可以直接求逆元。
没了。
T3
先考虑一种特殊的情况--链。
我们发现在为链的时候找到这条链的中点,将分成两部分的链互相指过去,可以证明这是答案的上界。
对于更平凡的情况,类似的,我们找到树的重心,那么对于被划分出来的几个子树,我们对它的处理和链上类似,
依旧是去找答案的上界,那么我们考虑容斥。
对于一个大小为 $ siz_i $ 的子树,我们令其中的 \(i\) 个点是强制不合法的,那么贡献为 $ (C_{x}{i})2i! $。
即为钦定 \(i\) 个点乘上钦定 \(i\) 个 \(p\) 乘上交换的顺序。
那么对于每个子树有 \(i\) 个点不合法的数量都可以快速计算,那么考虑直接合并到重心,用树形背包即可。
对于根,我们合并出来一个 \(f_i\) 来表示有 \(i\) 个点不合法的情况,所以答案就为 $ \sum\limits_{i=0}^{n} (-1)^if_i(n-i) $。
这里的复杂度为 \(O(N^2)\),考虑进一步优化。
可以发现树形背包本质上可以看作是一个卷积的形式,也就是可看作把若干个总长为 \(n\) 的多项式相乘。
我们这里用启发式的思想,每次选长度最小的多项式都去用 NTT相乘,最终可以优化到 \(O(Nlog^2N)\) 的复杂度。
9.28
T1
\(u\) 在 一条链上动时,\(\sum\limits_{i=l}^{r}=dis(u,i)\) 是凸的,因为凸函数的和还是凸函数。
那么我们从一个点出发,一直往小的方向走就能走到开会点。这个过程可以用树分治加速,当且仅当某个子树内 \([L,R]\) 的点超过一半,往这个方向走会变小
所以可以主席树维护。
但是直接分治碰到菊花图会退化,所以先三度化。
三度化就避免了单个点的度数太高导致分治被卡成暴力复杂度。
具体来说就是把 \(N\) 的图处理成一个 \(2N\) 的二叉树,通过每两个点之间加一个中间点来实现。
T2
CF618G
发现直接求不好求,那么就套路地转化一下,去考虑每个数出现地期望次数与对这个序列的贡献。
那么我们去尝试蒜一下某个数至少出现一次的概率、某个数出现恰好一次的概率、当最左边的数是 \(x\) 的时候出现的概率等辅助数组,然后就预处理出来四个dp数组,转移即可。
那么再发现一个数出现次数为50次及以上时概率几乎为0,可以忽略,那么最终答案是一个递推的形式,矩乘优化一下即可。
(其实我说这一堆废话还是因为有原题捏)
T3
CF1609G
由于它给出了一个很牛逼的单调性质,使得我们可以有一种并不怎么显然的贪心策略:每次直接挑选向右走或者向左走里值更小的。
证明的话其实你发现你走这条路本质上都得走一遍一个“基础值”,然后你走不同的道路的差别就是a数组和b数组的的差分数组之和。
也就是说我们这个贪心策略的本质还是走差分数组更小的值的道路。
那么我们发现 \(n,m\) 严重不同阶,那么对于小一点的 a 我们去暴力修改,大一点的 b 则作为我们需要维护的主体,每次 a 数组的修改直接插进 b 数组即可。
那么在插入的时候我们需要寻找前驱后继去找位置,那么直接开一个数据结构维护即可。
9.29
T1
说实话我没看出来这是个 \(n^2k^2\) 的dp。
那么 k 比较小的时候我们发现策略比较显然:
如果 k = 1,那么除了最长的链我们都被走了两次。
如果 k = 2,那么如果一开始有分叉的话,我们最优策略肯定是可以节省一个直径的距离。
接着考虑推广。
在最优方案里,如果进入一个子树大于两个,那么肯定不会都回来。
如果至少两个分身进入一个子树,那么这些子树应该都停留在这个子树内。否则的话,要么一个进去,否则都不出来。
那么我们直接枚举边考虑贡献,相当于把我们需要的东西预处理一下,需要的时候再累加,那么复杂度就会有保证了。
T2
有向图邻接矩阵的幂敛指数与周期。
半个结论题?
设 \(k\) 为幂敛指数,\(d\) 为周期。
那么求 \(d\) 的话结论是一个强连通分量的周期就是所有环的长度的gcd。
设共有 \(cnt\) 个强连通分量,那么整张图的周期就是 \(lcm(d_1,d_2...d_{cnt})\) 。
那么剩下的 \(k\) 显然可以倍增求解。
矩阵运算太慢的话考虑使用bitset优化即可。
ybt一些可能有用的idea
看上去一脸不可做的题先别走,见到和gcd有关的就想想奇偶分类,想想唯一分解,想想维护最小质因子。
见到多个离谱限制的观察一下是否和交集啥的有关系。
看看数据有没有任何能够状压的,想想有没有任何数可以根号分治的。
碰到毒瘤数据结构不要想着死磕,打完暴力剩下的时间做别的题效果好得多。
关于顺序问题考虑考虑数值和下标的对应关系,使劲瞅瞅有没有东西有单调性可以二分。
关与奇偶想一想位运算尤其是异或,有能力的话也想一想FWT(虽然我不会)
树上问题多想一想子树和的性质之类的,还有类似求后缀有关的东西不妨想一想倒着构建,转化为熟悉的已知的。
关于树上最长链条的转移问题,考虑最长+次长解决。类似的转移难以实行的时候可以考虑启发式合并降低复杂度。
遇到偏序问题维度太高,我们考虑去看是否有一些条件是可以相互推导出来的,比如说移项之后消掉剩下的就可以CDQ分治之类的做法。
如果不是必要不要打树套树,因为我很容易写挂。权值线段树加主席树一定程度下可以用树状数组替代。
看到题目没思路就看特殊性质即可。
10.3
T1
直接把字符串倒过来插到trie树上,然后在开头打上个标记,然后dfs去贪心选取即可,因为我们只关注数量,并不关注谁与谁匹配。
T2
ARC136E
数学题。
我们去考虑x可以到达y的条件,然后发现与因子有关,我们就去考虑按照奇偶性分类。
分完之后搞个牛逼的区间,然后神奇的发现区间有交就代表了可达。那么就可以通过这些神奇的区间交来搞出我们所求的。
T3
不可做题。
大体思路是回滚莫队,但我不会。
10.5
T1
一眼N次剩余板题,没什么好说的,就是被卡常了
把所有数乘起来发现就是个 $a^{\frac{(n)\times (n-1)}{2}} \equiv b (mod \ p) $ 的形式,直接爆蒜即可。
T2
发现排序之后对于一个 \(a_i\) 可以找到一个相匹配的 \(a_j\) ,那么 \(a_{j+1}\) 及其之后的也一定可以与 \(a_i\) 相匹配。
但是如果我们每次都去贪心的匹配可以发现可能会浪费匹配机会,也就是类似前面半部分的数都比较离散,但是后面的分布的很密集,后面的部分本来可以与前半部分相匹配但是贪心策略之下无法得到匹配。
所以我们把序列平分成两部分,分别用两部分的开头去枚举匹配即可,这样可以保证是有正确性的。
T3
令 \(f_i\) 表示现在在第 \(i\) 格,跳到到 \(i\) 为止能到到位置的前缀最大值所经过的挂的编号,\(g_i\) 则类似地表示前缀次大值所经过地编号。
每次查询时 ban 了一个挂,那么每次跳的边要么是 \(f\) 要么是 \(g\)。只要先倍增跳 \(f\),当要跳的 \(f\) 边被 ban 了时就倍增跳 \(g\) ,直到 \(f\) 不再被 ban 然后就接着倍增跳 \(f\) 即可,类似一个贪心的思路。
T4
就是搞个维护编号为 \(l-r\) 的点构成的联通块个数。
我们设 \(f_i\) 为以 \(i\) 做右端点,最小的左端点满足答案为 \(YES\),那么显然 \(f_i\) 单调上升。
考虑每一位都开一个并查集,那么这个并查集会从当前编号开始不断添加编号递减的边,直到不能再加的时候就可以求出 \(f_i\)。
那么考虑一下先去求出来 \(f_n\),直接倒着枚举判断就行
之后类似的求出来 \(f_i\),用线段树分治维护上面的操作即可。
10.6
T1
寻找一个序列变成单峰/谷所需要的最小步数,同时多次询问是以每次都在结尾插入的形式。
对于一个静态的序列,交换次数显然是对应的原数组下标的逆序对个数。
我们排序之后从两边向中间加数,那么就显然可以放左边可以放右边。
那么一个数的贡献也就是对于中间还没有加入的数的逆序对个数。
考虑动态起来,插入一个数去想一下它的影响。
下标是最大的,那么肯定是放在右半部分,而本身不会产生贡献。
但是在插入之前就比它大的数显然也会增加1的贡献。
那么也就是动态找下标比它大的数力第k的值比它大的数的下标,直接主席树二分。
T2
去类似贪心地想,每种杠杆都对任意时刻所需求的量取个max,可以最大限度减少我们在放、取圆盘上的无用时间,也就是我们最大化了它的“公共”部分。
那么发现相似的,我们可以把他看成一个区间DP的形式,去枚举断点即可。
T3
就是把匈牙利套了层皮放到所谓坐标点图上,没了。
T4
Skip
10.7
T1
n<=8,所以爆搜即可。
发现爆搜还是会T,那就加个折半搜索优化即可。
T2
经典线性期望,拆分成 \(e(x)+e(y)-e(lca(x,y))*2\),后发现正常的e可以直接套公式计算,只需要维护一个前缀和,而lca的贡献发现出现频率与a是有一致性的,也是直接递推即可。
T3
淀粉质就行。
T4
本质就是去枚举一下图不连通的方案数然后做个容斥。

10.10
T1
是在链上进行的,先把每只猫的限制改成一个我们更容易处理的形式,把所有的猫都放在节点 \(1\),也就是设个 $ a_i=t_i-h_i $,相当于求了每只猫如果等待时间为 \(0\) 的话一个饲养员该啥时候开始出发。
那么把这个玩意排个序,就可以用 \(f[i][j]\) 这个二维的状态表示前 \(i\) 只猫被 \(j\) 个饲养员带走的最小代价了。
那么式子也可以很快的写出来 $ f[i][j]=min(f[i][j],f[p][j-1]+a[i]*(i-p)-(sums[i]-sums[p])) $,其中 \(sums[i]\) 表示前 \(i\) 只猫等待的前缀和。
然后把式子移项即可得到 \(kx+b=y\) 的形式,斜率优化就行。
T2
CF1553F
可以套路地把mod拆成定义式,然后bit维护即可。
T3
可以发现如果存在一段区间 \([l,r]\) 合法,那么如果 \(l\le i,j\le r\),$ [i,j] $ 也是合法的区间。
那么就考虑一个二分的做法,对于每一个 \(i\) 都去求一个 \(w_i\) 表示对于 \(i\) 为左端点的合法区间的右端点最大值。
最终答案就是把 \(w_i-i\) 加起来就行。
10.11
T1

离散化完了就是典题,把列的贡献往行上堆,用线段树维护每行最近满足条件的点和距离,最后再加起来就行。
T2

考虑去找每种可能长度的贡献再加起来。
那么我们可以考虑容斥一下,对于全体选若干个长度为 \(L\) 的上升区间的方案,然后求容斥系数和。
那么如果两段上升区间有相交部分可以直接合并。
T3
ARC112F
发现这玩意是一个类似进位的东西,那么可以考虑把所有的贡献都“回退”到第一位,可以发现回退完之后贡献与原来的相同。
那么显然贡献就是
那么去求极值呗,我们需要在有解的情况下求最小值,用裴蜀定理可得需要使得 $ d=gcd(b_1,b_2...b_n,2^nn!-1) $,那么就是 $ v\equiv val_{first} (mod\ d) $。
下一步考虑根号分治
$ d>\sqrt{2^nn!} $
直接暴力枚举 \(val\),贪心换。
$ d\le\sqrt{2^nn!} $
搞同余最短路就好了。
10.12
10.14
T1
吓人题,$ k $ 段求和的 \(gcd\) 等于 $ K $ 段右端点的前缀和的 $ gcd $。
那么也就是求最大的数 \(x\) 使得 $ x|sum_n $,并且有 \(k-1\) 个 \(p\) 满足 $ x|sum_p $。
T2
比较经典的去考虑减少限制,首先建出来笛卡尔树干掉我们最大值的限制,然后剩下的区间异或用前缀的方式优化为单点操作,然后直接在笛卡尔树上01Trie合并,用启发式合并优化到log级别。
T3
去找循环节然后剥蒜即可。
T4
P5161
大体就是转化为了差分数组,然后转化为连续区间相同的个数,那么剥蒜一下再容斥,借鉴了优秀的拆分的思路,去找关键点然后分别计算不同长度的贡献即可。
其中有个求区间lcp的,P4248是相同的操作。用后缀数组加单调栈即可。
10.15
T1
欧拉筛,筛到 \(min(k,\sqrt{R})\) ,对于范围内的质数\(p\),后把在 $[max(L,2p),R] $ 内 \(p\) 的倍数标记一下然后剥蒜即可。
T2
CROC 2016-Elimination Round E
蒜一下当前的子序列个数,剩下的往里填数可以用矩阵优化。
求子序列个数的时候可以先强制选它当前是啥,然后去减去相同个数就是减去前驱的贡献。
求子序列个数是
解释一下的话就是如果有前驱的话减去前驱的贡献,因为你现在强制选上了当前的数,也就是避免了算重。
+1是当前是全新的元素,可以把他作为开头。
满足下一个条件你发现要保留最终答案最大,那么删的越少越好,那么就按照pre排个序,然后每次选最小的同时更新一下,发现这个过程是可以矩阵优化的。
T3
\YLCH/ \YLCH/ \YLCH/

推个式子然后最终就是kx+b的形式,线段树直接维护。
T4
显然建个虚树然后瞎跑就行。
显然就是让你找bfs深度最深的点的深度是啥,每次分类讨论答案点落在哪里。
落在虚树结点上直接树形DP,落在空的子树上我们需要预处理一下子树内的最远点然后把儿子按照这个值排序,如果落在了虚树边上我们只需要二分边上分界点在哪,预处理一下倍增数组求出来就行。。。
10.16
T1
随便挑一个节点当根,那么所有的叶子节点的状态是已经确定的,然后又能确定倒数第二层的状态,也就是说,如果有解的话解唯一,所以我们就把每个连通块 dfs 一遍,如果一条边下面连的子树有奇数个黑点,那么这条边就一定选,否则一定不选,最后判一下选出来的方案合不合法即可。
T2
考虑对删掉某种颜色后的联通块统计答案,因为能换颜色,所以就相当于走两个不同颜色的相邻连通块,但是答案不能直接加,需要减去重合部分,设一个连通块不走 \(1\) ,另一个连通块不走 \(2\) ,那么重合的部分就是只走 \(3\) 且两个连通块都包含的部分,这个也可以枚举每个点处理。
T3
考虑每条边的贡献,设这条边所连的深度较大的点是 \(x\),我们把 \(x\) 子树内的点都标记为 \(1\),子树外的点都标记为 \(0\), 那么这条边的贡献就是所有既包含 \(0\) 又包含 \(1\) 的区间,可以容斥一下,用总区间数减去只有 \(0\) 和只有 \(1\) 的区间,这个线段树维护前后缀 \(0,1\) 的个数即可,然后再写个线段树合并就可以过了。
T4
\(\operatorname{shuffle}(S)\) 操作本质上是个置换,而置换可以拆成若干个简单环,答案上界就是 \(\operatorname{lcm}(环的大小)\),而每个环的大小都是 \(\varphi(n-1)\) 的约数。
每个操作相当于原来为 \(i\) 位置的数转移到了 \(2i \bmod (n-1)\) 的位置(下标从 \(0\) 开始), 我们把每个环单独考虑,那么一次置换只看某个环的话就相当于把这个环循环左移,我们可以算出来循环串的最小循环节,然后算出这个环需要左移几次才能变成 \(T\),最后可以用 set 或者解同余方程的方式算出最终答案。
10.17
T1
看数据范围和取数方式知肯定是一道区间DP。
设 \(f(l,r)\) 为从区间 \([l,r]\) 中任意取数的最大价值。
若 \([l+1,r-1]\) 内的数都被取完,则可以同时取 \(l, r\) 处的数。
判断 \([l+1,r-1]\) 是否被取完只需判断满不满足 \(f(l,r)=\sum_{i=l}^r b_i\)。
零一种就是套路的转移: 枚举断点,将区间分成两部分,左右分别加起来就行。
T2
首先看到 \(0 \le c \le 9\) 可知每条边只会对答案的某一位产生贡献。因为要让最终答案最小,所以先保证答案的位数尽量少,再保证答案的高位尽量小,这启示我们进行 bfs 分层。
因为前导 \(0\) 不会使答案变大,所以先从 \(n-1\) 开始 bfs,只走 \(0\) 的边,这些点都可以作为终点,然后从 \(0\) bfs 分层,处理出每个点到 \(0\) 的最小距离(贡献在答案的哪一位),然后从高位到低位开始贪心,每次选一些当前层边权最小的点拓展(边权大的会使答案的当前位更大,后面的低位无法弥补,直接舍弃即可),如果有多个边权最小的就先拓展到 \(n-1\) 边数最少的,每次拓展一层,并记录每个点的前驱边,当到第 \(0\) 层时即找到最小方案,此时通过前驱边输出方案即可。
T3
我们定义一个点的点权是它连出去的边的异或和,这样定义可以使一条路径整体异或变为只有两个点异或。
现在我们需要做的就是每次同时给两个数异或一个相同的值,问最少几次能将他们全变成 \(0\)。
首先我们发现所有点权的总异或和为 \(0\), 所以答案显然有一个上界: \(n-1\),如果我们能把所有的点划分成 \(c\) 个点权异或和为 \(0\) 的集合,那么答案的上界就变成了 \(n-c\)。
想一下可以知道最小答案即为划分出最大的 \(c\)。
首先我们可以把相等的值两两匹配,最终会剩下最多 \(2^{16}\) 种数,我们可以进行一个状压 DP 的做,枚举子集来得到状态为 \(S\) 时最多可以分出多少点权异或和为 \(0\) 的集合。
10.18
T1
Nim游戏罢了
T2
ARC104F
遇到这种一一对应的题就去想一下树形结构,大多数情况下都是可以直接转化过来的。
那么我们要求的就是树的方案数。
那么考虑区间DP。
主要就是在转移的时候我们是由树转移到森林,主要的就是注意到不能直接由森林全转移到森林,因为可能会出现 \(2,2->4=1,3->4\) 算重的尴尬局面。
根据这题的特殊性,转移有两种,一种是一棵树转移到森林的一棵树后面接起来,另一种则是这棵树直接作为个体加入森林,树的数量增加了!
最后前缀和优化一下。
T3
ARC133E
数学思维题。
中位数,考虑把一个数关于一个标杆 \(k\) 的大小关系分为 \(1,0\) 两类,发现 \(1,1/0,0\) 情况下的中位数都可以直接求出来。
那么我们去尽量避免掉 \(0,1\) 的情况即可。
并且由于 \(0,1\) 的对称性可得, \(k=p\) 所导致的 \((a,0,0)\) 情况数量和 \(k=V-p\) 导致 \((a,1,1)\)的情况数量一样,那么直接算即可。
最后就是个神奇的小式子辣
T4
CF1140F
放到平面直角坐标系上发现就是对于所有出现 \(x,y\) 的位置都去配对,对于这一行或者这一列上有点的就是围成一个个实心的柱子。
那么考虑按照x,y搞成一个二分图的形式,然后发现答案就是连通块内左点数量×右点数量然后加起来。
关于撤销操作,搞个线段树分治去记录有效时间即可。
关于连通块操作。。。并查集就能维护,注意撤销操作的时候也要撤销并查集的更新,可以用栈结构维护。
10.20
T1
找最短公共非子序列,那么它删掉一个字符肯定是A和B的公共子序列,又因为只包含了0和1,那么显然我们可以预处理出来前驱位置便可以直接DP了。
又由于字典序最小,那么倒着推的时候贪心地选0就好了。
T2
直接dfs的时候统计有多少点已经走过了,那么已经走过的就可以连边而不会转移,最终答案就是 \(2^{cnt}\),用树状数组维护即可。
T3
发现每行每列最多只会刷一次,那么就假设每行是没有刷的,然后去对每一个点都检索一边即可。
T4
直接DP,发现最难处理的是递归合并,所以多开一维去存储是否能合并即可。
10.22
T1
给定一个 \(n \times m\) 的 \(01\) 矩阵,求包含 \([l,r]\) 个 \(1\) 的子矩形个数。
那么发现 \(n\) 较小,所以直接去枚举子矩形的上下边界,同时把矩阵右边界向右推的过程中去维护左边界的 \([l,r]\) 两个指针,复杂度为 \(n^2m\)。
LL calc(int x){
LL res = 0;
for(int l = 1; l <= n; l ++)
for(int r = l; r <= n; r ++){
for(int i = 1, j = 0, t = 0; i <= m; i ++){
// 此时的i相当于右边界,j为左边界。
b[i] = a[r][i] - a[l - 1][i], t += b[i];
while(t > x) t -= b[++ j];
res += i - j;
}
}
return res;
}
int main(){
scanf("%d%d", &n, &m);
for(int i = 1; i <= n; i ++){
scanf("%s", s + 1);
for(int j = 1; j <= m; j ++)
a[i][j] = (s[j] == '1') + a[i - 1][j];
}
scanf("%d%d", &l, &r);
LL res = calc(r);
if(l) res -= calc(l - 1);
printf("%lld\n", res);
}
T2
给定 \(n\) 个 正整数序列 \(a_1,a_2,...,a_n\),每个序列长度为 \(m\) 。 选择至少 \(1\) 个序列,然后在每个被选择的序列中选择恰好一个元素,求出所有被选择的元素的 \(gcd\) 。求所有方案的结果之和,答案对 \(10^9+7\) 取模。两种方案不同,当且仅当存在至少一个元素,在一种方案中被选择,在另一种中没有。
那么我们发现直接求 \(gcd=d\) 时的方案数并不好求,那么我们转化为 \(d|gcd\) 时的方案书,最后做一遍差分。
那么我们只需要满足所有选的数都是 \(d\) 的倍数,即对每一个数列都求 \(\sum_{n|d} f(d)\),其中 \(f(d)\) 为 \(d\) 在第 \(i\) 个序列中出现的次数。
那么这个过程就是一个迪利克雷前缀和的形式,可以直接用定义法做到 \(n\ ln\ n\)。
#define Maxn 24
#define Maxm 1000100
int n,m,mxn,Mxn,ansx;
int g[Maxm],t[Maxm];
int a[Maxn][Maxm];
int f[Maxn][Maxm];
inline void work()
{
n=read(),m=read();
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
a[i][j]=read(),mxn=max(mxn,a[i][j]);
for(int i=1;i<=n;i++)
{
memset(t,0,sizeof(t));
Mxn=0;
for(int j=1;j<=m;j++)
t[a[i][j]]++,Mxn=max(Mxn,a[i][j]);
for(int j=1;j<=Mxn;j++)
for(int k=j;k<=Mxn;k+=j)
f[i][j]+=t[k];
}
for(int i=mxn;i;i--)
{
g[i]=1;
for(int j=1;j<=n;j++)
g[i]=g[i]*(f[j][i]+1)%P;
g[i]--;
for(int j=i+i;j<=mxn;j+=i)
g[i]=(g[i]-g[j]+P)%P;
(ansx+=g[i]*i%P)%=P;
}
write(ansx);
return dwd;
}
这里补充一下迪利克雷前缀和,是用来求 \(f(i)=\sum\limits_{d|i}g(i)\) 形式的式子,那么我们的解决方法是先筛素数,然后用 \(g(i)\) 更新 \(f(i)\)。
for(int i=1;i<=cnt;i++)
for(int j=1;j*pri[i]<=n;j++)
g[pri[i]*j]+=g[i];
其实本质上就是个质因子拆分的逆形式,给他变成了累乘质因子。
注意这里的 \(pri[i]*j<=n\) 并不是说 \(j\) 是去枚举倍数,而是枚举因数,\(j\) 只是当前的一项因子。是为了限制上界不让他超过去。
T3
发起进攻。
在二维母世界诞生的你,第一次见到了三维世界的恢弘壮阔。可惜你无暇过多欣赏,你接收到的命令是:斩草除根!
三维世界可以看成是一个 \(A \times B \times C\) 的立方体,由于你的文明还没有完全掌握三维世界的结构,现在你还只有三种不够成熟的进攻路线:
\(1 a b\): 将所有 \(x\leq a, y\leq b\) 的世界毁灭。
\(2 a b\): 将所有 \(y\leq a, z\leq b\) 的世界毁灭。
\(3 a b\): 将所有 \(z\leq a, x\leq b\) 的世界毁灭。
最终你计划了 \(n\) 次进攻,你想知道你摧毁了这个世界多少的体积。
我们实际上是要对三个阶梯图形求并,那么我们首先考虑其中一种进攻路线的并,之后便可以得到一个二位的阶梯图形并且高相等。之后再考虑另外两种路线,实际上就是对于高度分层之后求一个阶梯和两个矩形的并。
T4
神题,不会。
10.24
T1
询问字符串任意组合能组合出来多少字符串三角形,这里我们把大小比较重载为字典序的大小。
神题,但是数据水可以哈希乱搞(
T2
你有 \(N\) 个朋友,他们会来你家玩,第 \(i\) 个人 \(1..A_i\) 天来玩,然后 \(A_i+1..2A_i\) 天不来,然后 \(2A_i+1..3A_i\) 又会来,以此类推
每天你会选一个来玩的人,给他颁个奖,如果没人来玩,你就不颁奖
你要给每个人都颁 \(K\) 个奖,问至少需要多少天
那么考虑去二分答案然后check,考虑把天和人拆成两部点,发现就是需要我们去检验是否有二分图完备匹配。
注意到有Hall定理为一个二分图有完美匹配,当且仅当二分图其中的一个点集的子集向另外一个点集连边,任意这样的子集所能够连到的对应的结点集合大小等于当前集合。
那么我们可以提前与处理一下你家的朋友的状态,之后考虑一天在 \(i\) 这个子集里面有边,当且仅当这一天所代表的自己与 \(i\) 有交集。
那么我们只需要知道 \(i\) 的补集所对应的天数,再用总天数去减掉,那么剩下的就是与 \(i\) 的交集。
所以我们只需要判断这个天数是否大于等于 \(nk\) 即可,其中 \(n\) 是状态中 \(1\) 的数量。
所以我们设 \(f_i\) 的自己代表的朋友匹配的天数,可以用高维前缀和处理。
const int Maxn = 20;
const int Maxs = 1 << Maxn;
const int Maxk = 1e5 + 10;
const int Maxm = Maxn * Maxk * 3;
int l, r, s;
int n, k, m, ansx;
int a[Maxn], djb[Maxm];
int t[Maxs], bit[Maxs];
inline bool check(int x)
{
memset(t, 0, sizeof t);
for (int i = 1; i <= x; i++) ++t[djb[i]];
for (int i = 0; i < n; i++)
{
int now = (1 << i) - 1;
for (int j = 0; j <= s; j++)
{
int cur = (j & now) | ((j & ~now) << 1);
t[cur | (1 << i)] += t[cur];
}
}
for (int i = 1; i <= s; i++)
if ((x - t[i ^ s]) < (bit[i]))
return 0;
return 1;
}
inline void work()
{
n = read(), k = read(), m = n * k * 3;
for (int i = 1; i <= n; i++) a[i] = read();
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
if (!(((j - 1) / a[i]) & 1))
djb[j] |= (1 << i - 1);
l = n * k, r = m, s = (1 << n) - 1;
for (int i = 1; i <= s; i++) bit[i] = bit[i & (i - 1)] + k;
while (l <= r)
{
int mid = (l + r) >> 1;
if (check(mid)) ansx = mid, r = mid - 1;
else l = mid + 1;
}
write(ansx);
return dwd;
}
T3
一场考试的时间为 \(T\) ,有 \(n\) 道题,每道题都可以花 \(t1_i\) 的时间获得 \(s1_i\) 的暴力分,并且可以在打完暴力后再花 \(t2_i\) 的时间多获得 \(s2_i\) 的分,但有 \(p_i\) 的概率写挂正解。求最大期望得分以及最大期望得分下的最小期望罚时(这里罚时定义为最后一次提交代码的时间)
那么我们设用时为 \(i\) 的时候期望最大得分为 \(f_i\),期望罚时为 \(g_i\)。
那么若是我们决定暴力,那么方程是
\( f_i=f_{i-t_1}+s_1,g_i=g_{i-t_1}+t_1 \)。
如果决定打正解,方程为
\( f_i=f_{i-t_1-t_2}+s_1+s_2\times p \)
\( g_i=(g_{i-t_1-t_2}+t_1)\times(1-p)+i\times p \)
那么我们现在的问题就是安排一个合理的开题顺序使得罚时最小。
那么设最后开的两道题分别为 \(i,j\),如果 \(j\) 对了,罚时就是 \(i,j\) 的总耗时;如果 \(i\) 对了但是 \(j\) 挂了,那么罚时就是 \(i\) 的耗时;当两个题都挂了的时候,那么他们对答案没有贡献。
所以可以有个式子
\( p_j\times(t2_i+t2_j)+(1-p_j)\times p_i \times t2_i \)
那么是 \(i\) 在前还是 \(j\) 在前?假设前者的罚时更小,那么有
\(
p_j\times (t2_i+t2_j)+(1-p_j)\times p_i\times t2_i < p_i\times (t2_j+t2_i)+(1-p_i)\times p_j\times t2_j
\)
整理一下就是
\(
(1-p_i)\times p_j \times t2_i<(1-p_j)\times p_i \times t2_j
\)
\( (1-p_i)\times t2_i/p_i <(1-p_j) \times t2_j/p_j \)
直接按照式子排序即可。
10.26
T1
就是给定一个树的结构,你需要从一个给定点开始往外拓展,按照题目给定顺序去在已经拓展完的点的出边里选一条去拓展,但是你可以自由选择,最终让树的直径长度最大。
其实就是个区间DP,你把那条直径抽出来之后其他的枝干就是为了存放权值小的点,而这条直径就是一条序列。
我们这里称不在直径上的点为劣点。
那么我们会发现无法确定路径的两个端点能够存储多少个这种劣点,因为端点可以向任意方向拓展。
所以我们需要把端点所拓展的方向也放进我们的状态里,那么DP就可以设出来状态 \(f(u,v,t,m)\),其中 \(m\in [0,3]\),\(t\) 表示已经在序列A中用掉了 \(t\) 个数。
那么
$ f(u,v,t,0) $ 表示 \(u->v\) 的最大长度,并且路径不再想两端拓展。
$ f(u,v,t,1) $ 表示 $ u->p_v $ 的最大长度(\(p_v\) 表示 \(u->v\) 中 \(v\) 的前一个结点),并且端点 \(u\) 不再拓展,但是 \(p_v\) 会向 \(v\) 拓展。也就是说不能向 \(p_v->v\) 这条边以及后续的边放劣点。
$ f(u,v,t,2) $ 表示 $ p_u->v $ 的最大长度(\(p_u\) 表示 \(u->v\) 中 \(u\) 的后一个结点),并且端点 \(v\) 不再拓展,但是 \(p_u\) 会向 \(u\) 拓展。也就是说不能向 \(p_u->u\) 这条边以及后续的边放劣点。
$ f(u,v,t,3) $ 表示 $ p_u->p_v $ 的最大长度,并且端点 \(p_u\) 向 \(u\) 拓展,端点 \(p_v\) 向 \(v\) 拓展。
那么最终答案就是 $ max(f(u,v,n,0)) $。
T2
ARC126E
直接把贡献差了,发现肯定是运算次数更多的时候对整个答案的贡献越大。
剩下的就是维护操作辣
T3
给一个长度为 \(N\) 的排列\(A\),现在你要在序列上选一些数,当前局面下,一个数可选当且仅当选完该数后已选的数构成的子序列单调递增。若有可选的数,等概率选出一个,否则结束。问期望选出多少个数
直接区间DP
设 $C =\sum\limits_{L<K<R,A_L<A_K<A_R} $
$ F_{L,R}=( \sum\limits_{L<K<R,A_L<A_K<A_R} F_{L,K}+F_{K,R})/C+1 $
int n, m;
struct Bit
{
int c[Maxn];
#define lowbit(x) x &(-x)
inline void INIT()
{
for (int i = 0; i <= n; i++)
c[i] = 0;
}
inline void add(int x, int k)
{
while (x <= n)
(c[x] += k) %= P, x += lowbit(x);
return;
}
inline int ask(int x)
{
int res = 0;
while (x)
(res += c[x]) %= P, x -= lowbit(x);
return res;
}
inline int query(int l, int r)
{
return (ask(r) - ask(l - 1) + P) % P;
}
#undef lowbit
} L, R[Maxn], cnt;
int a[Maxn];
int f[Maxn][Maxn];
int fac[Maxn], invfac[Maxn];
inline void INit()
{
fac[0] = 1;
for (int i = 1; i <= n; i++)
fac[i] = fac[i - 1] * i % P;
invfac[n] = qp(fac[n], P - 2);
for (int i = n - 1; i >= 1; i--)
invfac[i] = invfac[i + 1] * (i + 1) % P;
invfac[0] = 1;
for (int i = n; i >= 1; i--)
invfac[i] = invfac[i] * fac[i - 1] % P;
return;
}
inline void work()
{
n = read();
for (int i = 1; i <= n; i++)
a[i] = read();
n++, a[n] = n;
INit();
for (int l = n - 2; l >= 0; l--)
{
cnt.INIT();
L.INIT();
for (int r = l + 2; r <= n; r++)
{
R[r].add(a[l + 1], f[l + 1][r]);
L.add(a[r - 1], f[l][r - 1]);
cnt.add(a[r - 1], 1);
int Down = cnt.ask(a[r] - 1) - cnt.ask(a[l]);
if (Down <= 0)
continue;
int s1 = L.query(a[l] + 1, a[r] - 1);
int s2 = R[r].query(a[l] + 1, a[r] - 1);
s1 = (s1 + s2) % P;
f[l][r] = (s1 * invfac[Down] % P + 1) % P;
}
}
write(f[0][n]);
return dwd;
}
11.1
T1
Alice和Bob要竞选魔方市市长。
有\(n\)个选民,编号为\(1~n\),它们中有的人支持Alice,有的人支持Bob,还有的人保持中立。
现在你需要把选民分成若干个区间,每个区间的长度在\([l,r]\)中。如果一个区间中支持Alice的人比支持Bob的人多,那么Alice得一票,一个区间中支持Bob的人比支持Alice的人多,那么Bob得一票。
Alice想要赢得选举,于是它请你合理地分区间,使得它获得的票数减去Bob获得的票数最大。
暴力非常好写,考虑优化。
那么可以按照数的前缀和 \(s\) 建线段树,同时每个电上都都存一个单调队列。
那么每次操作相当于是跨一个段,将 \(f[i-l]\) 加入我们的值域线段树,就可以直接更新出 $ f[i] $,之后为了保证区域正确,需要删除 $ f[i-r] $。
const int Maxn = 1e6 + 10;
const int inf = 0x3f3f3f3f;
const int Maxs = 1e6;
int a[Maxn], f[Maxn];
multiset<int> st[Maxn << 2];
inline void gtmax(int &x, int y, int z, int t)
{
x = x > y ? x : y;
x = x > z ? x : z;
x = x > t ? x : t;
return;
}
struct Seg
{
int t[Maxn << 3];
int type;
#define ls(i) (i << 1)
#define rs(i) (i << 1 | 1)
inline void up(int i)
{
t[i] = max(t[ls(i)], t[rs(i)]);
return;
}
inline void add(int i, int l, int r, int x, int k)
{
if (l == r)
{
if (type == 1)
st[i].insert(k);
else
st[i].erase(st[i].find(k));
if (st[i].size())
t[i] = *(--st[i].end());
else
t[i] = -inf;
return;
}
int mid = (l + r) >> 1;
if (x <= mid)
add(ls(i), l, mid, x, k);
else
add(rs(i), mid + 1, r, x, k);
up(i);
return;
}
inline int ask(int i, int l, int r, int L, int R)
{
if (L <= l and r <= R)
return t[i];
int mid = (l + r) >> 1;
if (R <= mid)
return ask(ls(i), l, mid, L, R);
if (L > mid)
return ask(rs(i), mid + 1, r, L, R);
return max(ask(ls(i), l, mid, L, R), ask(rs(i), mid + 1, r, L, R));
}
} T;
inline void work()
{
int n = read(), ll = read(), rr = read();
memset(f, -0x3f, sizeof(f));
memset(T.t, -0x3f, sizeof(T.t));
for (int i = 1; i <= n; i++)
a[i] = read(), a[i] = a[i - 1] + a[i];
f[0] = 0, T.type = 1;
if (ll == 1)
T.add(1, -Maxs, Maxs, a[0], f[0]);
for (int i = 1; i <= n; i++)
{
f[i] = max({f[i], T.ask(1, -Maxs, Maxs, -Maxs, a[i] - 1) + 1, T.ask(1, -Maxs, Maxs, a[i] + 1, Maxs) - 1,
T.ask(1, -Maxs, Maxs, a[i], a[i])});
// gtmax(f[i],T.ask(1,-Maxs,Maxs,-Maxs,s[i]-1)+1,T.ask(1,-Maxs,Maxs,s[i]+1,Maxs)-1,T.ask(1,-Maxs,Maxs,s[i],s[i]));
if (i - rr >= 0)
T.type = 0, T.add(1, -Maxs, Maxs, a[i - rr], f[i - rr]);
if (i - ll + 1 >= 0)
T.type = 1, T.add(1, -Maxs, Maxs, a[i - ll + 1], f[i - ll + 1]);
}
write(f[n]);
return dwd;
}
T2
小象有\(n\)张卡片,第\(i\)张卡片上有一个数字\(ai\)。Alice和Bob轮流选择卡片 (不能重复),如果某次选择后已选择的卡片上的数字的最大公约数为1或者没有卡片可以选择,那么当前角色失败。
你需要求出:1、如果双方都选择最优策略,谁会获胜;2、如果双方都随机选取,Alice获胜的概率。
暴力是直接对着卡片状压,考虑优化。那么我们发现当前状态只与当前的gcd和已选的卡片数量有关,然后直接记录这两个信息即可。但是实际上状态数应该是把 \(a_i\) 中相同的质因数去掉,最终状态数还可以更少,可以达到我们的预期。
const int Maxn = 110;
const int Maxs = 100010;
int n, a[Maxn];
int tmp[Maxs];
int f[Maxs][Maxn];
double g[Maxs][Maxn];
#define dwd void()
inline void work()
{
int T;
cin >> T;
while (T--)
{
memset(g, 0, sizeof(g)), memset(f, 0, sizeof(f)), memset(tmp, 0, sizeof(tmp));
scanf("%d", &n);
for (int i = 1; i <= n; i++)
scanf("%d", &a[i]);
for (int i = 1; i <= n; i++)
for (int j = 1; j * j <= a[i]; j++)
if (a[i] % j == 0)
{
tmp[j]++;
if (j * j != a[i])
tmp[a[i] / j]++;
}
for (int i = 1; i <= n; i++)
f[1][i] = g[1][i] = 1;
for (int i = 2; i <= 100000; i++)
for (int j = tmp[i]; j >= 1; j--)
{
g[i][j] = (1 - g[i][j + 1]) * (tmp[i] - j);
if (j != tmp[i])
f[i][j] = f[i][j + 1] ^ 1;
for (int k = 1; k <= n; k++)
if (a[k] % i)
{
int v = __gcd(a[k], i);
g[i][j] += 1 - g[v][j + 1];
f[i][j] |= f[v][j + 1] ^ 1;
}
if (j < n)
g[i][j] /= n - j;
}
bool ans1 = 0; double ans2 = 0;
for (int i = 1; i <= n; i++)
{
ans1 |= f[a[i]][1] ^ 1;
ans2 += (1 - g[a[i]][1]) / n;
}
printf("%d %.4f\n", ans1, ans2);
}
return dwd;
}
T3
神他妈带修的天天爱跑步,我还是天台爱跑步罢,20pts无修改滚蛋
Task1:无操作2、3,重回联赛赛场
Task2、3:操作2、3只出现一个:正解少考虑一些情况
Task4:直接用LCT维护树,然后每次询问暴力o(n)更新答案,logn加边删边, O(1)修改。
All:我们发现这道题很难用一些数据结构对答案进行维护,比较通用的方法是分块。我们考虑把所有操作每S个分一块。由于天天爱跑步的做法需要在静态树上完成,且必须固定每个点的W值,所以我们可以在每一块开始之间把树的形态已经每个点在最初的W值预处理完成。我们把同一个块内的所有询问放到一起做一遍noip题。那么现在需要考虑的就是同一个块内发生2、3操作对答案的影响。对于每个操作3,可以暴力扫一遍所有询问,判断这个点在W修改之前是否会观察到这个询问的玩家、修改之后是否会观察到这个询问的玩家。如果在修改前能够观察到而修改之后不能观察到,那么在做noip题时它会使答案多增加1,我们在这里预先-1即可。同理,如果修改前不能观察到而修改后能够观察到,那么在做noip题时它将忽略这次询问的贡献,我们需要预先给它+1。然后考虑2号操作,由于2号操作会导致两点之间路径的变化,所以不能直接用静态树完成。但是注意到块的大小为S,那么最多发生S次删边加边,那么我们可以把整张图缩点,如果一条边在这个块内不发生变化,那么就把它连接的两个点缩起来。这样我们就可以得到一张点数为O(s)级别的图。每次询问时我们可以暴力BFS整张图来寻找两个点之间的路径经过了哪些连通块,并给这些连通块打上询问标记。把整个块扫完之后对每个连通块分别做一遍noip题即可。
在处理时有一些小细节,我们在S个操作结束后,先用tarjan求lca,得到在一个连通块内两点之间的距离,然后再依次扫一遍询问经过的所有连通块得到一个询问在某个连通块的开始时间和结束时间。得到了这些信息之后我们才能处理操作3,判断一个点在W修改前和修改后能否观察到一个询问的玩家,判断方法是一个点在一条链上(用DFS序判断一个点是否在一条链上+用深度来判断到达当前点的时刻)。
11.3
T1
一个图上有一堆障碍,多次询问每次询问一个大正方形能否在不触碰障碍的情况下平移到某个位置,给你这个玩意的边长和起始位置终止位置的右下角的坐标。
发现询问可以离线,那么我们考虑预处理出来每个点作为右下角可以存放的最大正方形的边长,那么这个问题就变成了点图上的可达性问题。
那么询问离线之后可以对一些相同的坐标点按照问问的正方形的边长大小去排序,之后发现如果大的可以到达那么小的一定可达,可以加速这个过程。
typedef pair<int,int> pir;
const int N = 1005;
const int Q = 1e5+10;
const int dx[] = {0, 1, 1};
const int dy[] = {1, 0, 1};
const int dx2[] = {1, -1, 0, 0};
const int dy2[] = {0, 0, 1, -1};
namespace dsu {
int fa[N*N], siz[N*N];
void init(int n)
{
for(int i = 1; i <= n; i++)
fa[i] = i, siz[i] = 1;
}
int find(int x)
{
return fa[x] == x ? x : fa[x] = find(fa[x]);
}
void merge(int x, int y)
{
x = find(x), y = find(y);
if(x == y) return void();
if(siz[x] < siz[y]) swap(x, y);
siz[x] += siz[y]; fa[y] = x;
}
bool check(int x, int y)
{
return find(x) == find(y);
}
}
struct query { int x1, y1, x2, y2, w, id; };
int n, m, q;
int siz[N][N];
char s[N][N];
query qry[Q];
vector<pir> id[N];
bool ans[Q];
void prework();
#define pos(i,j) ((i-1)*m+j)
int main()
{
cin >> n >> m >> q;
for(int i = 1; i <= n; i++)
cin >> (s[i]+1);
prework();
for(int i = 1; i <= q; i++)
{
cin >> qry[i].x1 >> qry[i].y1;
cin >> qry[i].x2 >> qry[i].y2;
cin >> qry[i].w; qry[i].id = i;
}
sort(qry+1, qry+q+1, [](query a, query b){
return a.w > b.w;
});
dsu::init(n*m);
for(int i = 1, j = min(n,m); i <= q; i++)
{
while(j > 0 and j >= qry[i].w)
{
for(auto x : id[j])
{
for(int k = 0; k < 4; k++)
{
int nx = dx2[k]+x.first;
int ny = dy2[k]+x.second;
if(1 <= nx and nx <= n and 1 <= ny and ny <= m and siz[nx][ny] >= j)
dsu::merge(pos(x.first,x.second), pos(nx,ny));
}
}
j--;
}
if(qry[i].x1 != qry[i].x2 or qry[i].y1 != qry[i].y2)
ans[qry[i].id] = dsu::check(pos(qry[i].x1,qry[i].y1), pos(qry[i].x2,qry[i].y2));
else
ans[qry[i].id] = (siz[qry[i].x1][qry[i].y1] >= qry[i].w);
}
for(int i = 1; i <= q; i++)
cout << (ans[i] ? "Yes" : "No") << "\n";
}
void prework()
{
memset(siz, -1, sizeof(siz));
queue<pir> q; int x;
for(int i = 1; i <= n; i++)
for(int j = 1; j <= m; j++)
if(s[i][j] == '1')
q.push({i, j}), siz[i][j] = 0;
for(int i = 1; i <= n; i++)
q.push({i, 0}), siz[i][0] = 0;
for(int i = 1; i <= m; i++)
q.push({0, i}), siz[0][i] = 0;
while(!q.empty())
{
auto a = q.front(); q.pop();
for(int k = 0; k < 3; k++)
{
int nx = dx[k]+a.first;
int ny = dy[k]+a.second;
if(nx <= n and ny <= m and siz[nx][ny] == -1)
{
siz[nx][ny] = siz[a.first][a.second]+1;
q.push({nx, ny});
}
}
}
for(int i = 1; i <= n; i++)
for(int j = 1; j <= m; j++)
if(siz[i][j] != -1) id[siz[i][j]].push_back({i, j});
}
T2
对于一个01串,定义
\( f(s)=\sum\limits_{i=0}^{\frac{|>s|}{2}-1} s_i=s_{ |s| - 1 - i} \)
求其所有非空子序列的 \(f(s)\) 之和,对 \(998244353\) 取模。
那么考虑把贡献转化到每一对数上,把 \(C\) 拆开之后用多项式乘法加速即可。
typedef long long ll;
const int Maxn = 6e5 + 10;
const int P = 998244353;
int n, len;
char s[250010];
ll pw[20][Maxn], Fac[Maxn], invfac[Maxn], pw2[Maxn];
ll f[Maxn], g[Maxn],ans;
inline ll Add(const ll &x, const ll &y) { return (x + y < P) ? x + y : x + y - P; }
inline ll Sub(const ll &x, const ll &y) { return (x - y < 0) ? x - y + P : x - y; }
inline ll qp(ll x, ll y) { ll res = 1; for (; y; y >>= 1, x = x * x % P) if (y & 1) res = res * x % P; return res; }
inline void Init(const int MAXN=500000)
{
for (int w = 2, hh = 1; w <= MAXN+30000; w <<= 1, hh++) { ll pwr = qp(3, (P - 1) / w); pw[hh][0] = 1; for (int j = 1; j < (w >> 1); j++) pw[hh][j] = pw[hh][j - 1] * pwr % P; }
Fac[0] = 1; for (int i = 1; i <= MAXN; i++) Fac[i] = Fac[i - 1] * i % P;
invfac[MAXN] = qp(Fac[MAXN], P - 2);
for (int i = MAXN-1; ~i; i--) invfac[i] = invfac[i + 1] * (i + 1) % P;
pw2[0] = 1; for (int i = 1; i <= MAXN; i++) pw2[i] = pw2[i - 1] * 2 % P;
}
inline void NTT(ll *a, int n, int Type)
{
static int r[Maxn];
for (int i = 1; i < n; i++) r[i] = (r[i >> 1] >> 1) | ((i & 1) ? (n >> 1) : 0);
for (int i = 1; i < n; i++) if (i < r[i]) swap(a[i], a[r[i]]);
for (int w = 2, i = 1; w <= n; w <<= 1, i++) for (int k = 0; k < n; k += w) for (int j = k; j < k + (w >> 1); j++)
{ ll u = a[j], t = a[j + (w >> 1)] * pw[i][j - k] % P; a[j] = Add(u, t); a[j + (w >> 1)] = Sub(u, t); }
if (Type == -1) { reverse(a + 1, a + n); ll Inv = qp(n, P - 2); for (int i = 0; i < n; i++) a[i] = a[i] * Inv % P; }
}
inline void work()
{
scanf("%s", s + 1); n = strlen(s + 1); Init(); for (len = 1; len <= n; len <<= 1);
memset(f, 0, sizeof(f)); memset(g, 0, sizeof(g));
for (int i = 1; i < n; i++) g[i] = pw2[i - 1] * Fac[n - 1 - i] % P;
for (int i = 1; i <= n; i++) if (s[i] == '0') f[i] = invfac[i - 1];
NTT(f, len << 1, 1); NTT(g, len << 1, 1);
for (int i = 0; i < (len << 1); i++) f[i] = f[i] * g[i] % P; NTT(f, len << 1, -1);
for (int i = 1; i <= n; i++) if (s[i] == '0') ans = Add(ans, f[i] * invfac[n - i] % P); memset(f, 0, sizeof(f));
for (int i = 1; i <= n; i++) if (s[i] == '1') f[i] = invfac[i - 1]; NTT(f, len << 1, 1);
for (int i = 0; i < (len << 1); i++) f[i] = f[i] * g[i] % P; NTT(f, len << 1, -1);
for (int i = 1; i <= n; i++) if (s[i] == '1') ans = Add(ans, f[i] * invfac[n - i] % P);
printf("%lld", ans);
}
T3
大力分讨+阅读理解
const int Maxn = 5010;
const int P = 998244353;
int n, k, ansx;
int g[Maxn], f[Maxn];
int ls[Maxn], rs[Maxn];
int s1[Maxn], s2[Maxn];
void dfs(int x, int fa, bool dep, int a, int b)
{
if (!ls[x]) { f[x] = 1; g[x] = k * k; s1[x] = k * a, s2[x] = k * b; return; }
dfs(ls[x], x, !dep, a, b); dfs(rs[x], x, !dep, a, b);
if (dep) { f[x] = (f[ls[x]] * s2[rs[x]] + s2[ls[x]] * f[rs[x]]) % P; s1[x] = (s1[ls[x]] * g[rs[x]] + g[ls[x]] * s1[rs[x]]) % P; s2[x] = 2 * s2[ls[x]] * s2[rs[x]] % P; }
else { f[x] = (f[ls[x]] * s1[rs[x]] + s1[ls[x]] * f[rs[x]]) % P; s1[x] = 2 * s1[ls[x]] * s1[rs[x]] % P; s2[x] = (s2[ls[x]] * g[rs[x]] + g[ls[x]] * s2[rs[x]]) % P; }
g[x] = 2 * g[ls[x]] * g[rs[x]] % P;
}
inline void work()
{
n=read(),k=read();
for (int i = 2,x; i <= n; i++) { x=read()+1; ls[x] = rs[x]; rs[x] = i; }
for (int i = 1; i <= k; i++) for (int j = 1; j <= k; j++) { dfs(1, 0, 0, i, j); ansx = (ansx + f[1]) % P; }
write(ansx);
return dwd;
}
signed main()
{
work();
return 0;
}
11.5
T1
给一个二维平面,每次走曼哈顿距离为 \(k\) 的一步,然后让在最小步数内到指定坐标并且求出路径
那么发现点图可能存在负下标,先不管,输出答案时统一处理即可。
那么每次的操作都相当于把\(k\)瓜分为\(x\),\(y\)。那么只有 \(k\) 为偶数且 \(x+y\) 为奇数时无解,因为怎么拆最终下标的和都只能是偶数。
那么我们尝试反过来走,把步骤压在栈里面再输出。
那么考虑进行一个搜索的做,为了方便处理我们直接钦定 \(x<y\),在过程中如果违反了规则就直接swap。当 \(x+y>=2*k\) 的时候,因为我们终点此时成了 \((0,0)\),那么无论是哪边走多少都是可以快速接近终点。但是这里我们为了让在接近之后更快速的调整,决定使得\(x,y\)更均摊,直接俄使\(y-k\)即可。
如果\(x+y==k\),那么就是直接到了终点前的一步了,可以直接走。
那么剩下的情况就需要我们去调整步数。那么就是在两步之内直接到达我们的目标位置,可以列一个二元一次方程组来求出我们中转的位置,结论是 $ (-(k-(x+y)/2),(x+y-(x+y)/2)) $。
#define pr pair<int, int>
#define mp make_pair
int k, X, Y, tp;
pr st[1 << 20];
inline pr f(int x, int y)
{
if (x > y)
{
pr res = f(y, x);
return mp(res.second, res.first);
}
else if (x < 0)
{
pr res = f(-x, y);
return mp(-res.first, res.second);
}
else if (x + y >= 2 * k)
{
pr res = mp(x, y - k);
return mp(res.first, res.second);
}
else if (x + y == k)
{
pr res = mp(0, 0);
return mp(res.first, res.second);
}
else
{
pr res = mp(-(k - (x + y) / 2), x + y - (x + y) / 2);
return mp(res.first, res.second);
}
}
int main()
{
scanf("%d%d%d", &k, &X, &Y);
if (k % 2 == 0 and abs((X + Y)) % 2 == 1)
{
printf("-1");
return 0;
}
tp = 1;
st[tp] = make_pair(X, Y);
while (!(X == 0 and Y == 0))
{
st[++tp] = f(X, Y);
X = st[tp].first, Y = st[tp].second;
}
printf("%d\n", --tp);
while (tp)
{
printf("%d %d\n", st[tp].first, st[tp].second);
tp--;
}
return 0;
}
T2
有 \(n\) 种需要满足的条件, \(m\) 个人,提供 \(a_{i,j}\) 的代价可以让第 \(j\) 个人满足第 \(i\) 个条件。同时如果第 \(j\) 个人出手,需要付出 \(b_j\) 的全局花费,即只需要缴纳一次即可。求最小代价。
对于每一行考虑排序之后差分一下原数组。
那么找到第一个在已选人的状态集合之内的数,给他加上第 \(i\) 个差分值,那么发现最终这个状态的答案就是他的补集的子集贡献之和,再与处理一下对于每个状态的 \(b\) 之和即可。
之所以要加的是补集的子集和,是因为你需要统计的贡献是没有选中的前缀差分和。
#define lowbit(x) (x&(-x))
#define Maxn 100010
#define Maxm 31
#define Maxs 34000000
int n,m;
int a[Maxm],b[Maxm];
int id[Maxm];
ll f[Maxs],g[Maxs],ans;
inline bool cmp(int x,int y)
{
return a[x]<a[y];
}
inline void work()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++)
id[i]=i;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
scanf("%d",&a[j]);
sort(id+1,id+1+m,cmp);
int S=0;
for(int j=1;j<=m;j++)
f[S]+=a[id[j]]-a[id[j-1]],S|=(1<<(id[j]-1));
}
for(int i=0;i<m;i++)
scanf("%d",&b[i]);
int S=(1<<m),s=1;
for(int w=0;s<S;w++,s<<=1)
for(int i=0,len=s<<1;i<S;i+=len)
for(int j=0;j<s;j++)
f[i+j+s]+=f[i+j];
g[0]=0;
for(int i=1;i<S;i++)
g[i]=g[i^lowbit(i)]+b[__builtin_ctz(i)];
ans=LLONG_MAX;
for(int i=1;i<S;i++)
ans=min(ans,f[(S-1)^i]+g[i]);
cout<<ans;
return ;
}
T3
给定两个序列\(a,b\),求一个排列,使得 $\sum\limits_{1}^{n}\lceil \frac{max(b_i-c_{a_i},0)}{k} \rceil $ 最小,输出答案与方案。
那么可以弹性你,首先把问题转化为每次操作把某个 $b_i -k $,然后求最小的操作次数使得存在排列 \(b_i\le a_{c_i}\)。
那么对比目前的 \(a,b\) 中最大值,若 \(a\) 的最大值大于 \(b\),那么显然可以直接把这两个数配对,否则就把 \(b\) 的最大值减少 \(k\)。
考虑如何加速这个过程,可以直接把 $ \frac{b_i}{k} $ 相同的 $ b_i $ 一起处理。
#define Maxn 1000010
struct Node
{
int x, id;
Node()
{
}
Node(int x, int i) : x(x), id(i)
{
}
friend bool operator<(const Node a, const Node b)
{
return a.x == b.x ? a.id < b.id : a.x < b.x;
}
friend bool operator>(const Node a, const Node b)
{
return a.x == b.x ? a.id > b.id : a.x > b.x;
}
friend bool operator==(const Node a, const Node b)
{
return a.x == b.x && a.id == b.id;
}
};
Node a[Maxn];
map<int, set<Node>> Set;
int n, k;
int ansx, ps[Maxn];
inline void work()
{
n = read(), k = read();
for (int i = 1; i <= n; i++)
a[i].x = read(), a[i].id = i;
for (int i = 1; i <= n; i++)
{
int x = read();
Set[x / k].emplace(x % k, i);
}
sort(a + 1, a + 1 + n, greater<Node>());
for (int i = 1; i <= n; i++)
{
while (Set.size())
{
auto b = Set.rbegin()->first;
auto &s = Set.rbegin()->second;
if (!s.size())
{
Set.erase(--Set.end());
continue;
}
if (a[i].x >= b * k + s.begin()->x)
{
auto p = --s.lower_bound(Node(a[i].x - b * k + 1, 0));
ps[p->id] = a[i].id;
s.erase(p);
break;
}
auto t = max(1ll, b - a[i].x / k);
ansx += t * s.size();
auto &Tmp = Set[b - t];
if (s.size() > Tmp.size()) swap(s, Tmp);
Tmp.insert(s.begin(), s.end());
Set.erase(--Set.end());
}
}
write(ansx), putchar('\n');
for (int i = 1; i <= n; i++)
write(ps[i]), putchar(' ');
return dwd;
}
11.8
T1
首先发现 $ (n,k)!=1 $ 时肯定无解,证明如下:
我们设 \(s[i]\) 里所有 \(1\) 的位置的下标和为 $ W_i $,假设 $ s[i] $ 可以通过循环移位得到 $ s[i+1] $,那么必然可以存在整数 \(x\),使得 $ W_i+x\times k\equiv W_{i+1}(mod\ n) $。又有 $ W_{i+1}\equiv W_{i+1}(mod\ n) $,那么由两式可以得到 \(x\times k \equiv 1(mod\ n)\),那么这是有解的必要条件。
当 \(n,k\) 互质时,我们所要求的本质就是满足那个下标和的式子。那么就是把满足有解的条件的 \(k\) 挪过去,得到 \(s[0]\) 的 $ \frac{0}{k},\frac{1}{k}...\frac{k-1}{k} $ 位置为 \(1\),哦同样的对于 \(s[i]\),我们使得 $ \frac{i}{k},\frac{i+1}{k}...\frac{k+i-1}{k} $ 处为 \(1\),那么显然从 $ s[i]->s[i+1] $ 可以通过向右循环移位 $ \frac{1}{k} $ 实现,同时发现了 $ \frac{i}{k}+1=\frac{k+(i+1)-1}{k} $,那么我们也就把 $ s[i] $ 的 $ \frac{i}{k} $ 变成 \(0\), $ \frac{i}{k}=1 $ 变成 \(1\) 即可用 \(b\)操作实现变换。
int T;
int n, k, l;
char s[Maxn];
inline int exgcd(int a, int b, int &x, int &y)
{
int d = a;
if (!b) y = 0, x = 1;
else d = exgcd(b, a % b, y, x), y -= a / b * x;
return d;
}
inline int inv(int a,int P)
{
int x,y;
exgcd(a,P,x,y);
return (x+P)%P;
}
inline void work()
{
cin >> T;
while (T--)
{
scanf("%d%d%d", &n, &k, &l);
if(__gcd(n,k)!=1) puts("NO");
else
{
puts("YES");
int Inv=inv(k,n);
for(int i=1;i<=l;i++)
{
memset(s,'0',sizeof(s));
for(int j=0;j<k;j++)
s[(i+j)*Inv%n]='1';
s[n]='0';
for(int j=0;j<n;j++)
cout<<s[j];
cout<<'\n';
}
}
}
return dwd;
}
T2
const int Maxn = 60;
int n, m;
int pre[Maxn], Id[Maxn];
int pos[Maxn], len[Maxn];
string s[Maxn], str[Maxn], ansx;
string tmp, cpy;
inline int cmpr(int a, int b)
{
string txt1 = str[a], txt2 = str[b];
int len1 = txt1.size(), len2 = txt2.size();
while (txt1.size() != txt2.size())
{
if (txt1.size() < txt2.size()) txt1 = txt1 + str[a];
else txt2 = txt2 + str[b];
}
if (txt1 > txt2) return 1;
else if (txt1 < txt2) return -1;
else return 0;
}
inline bool cmp(int a, int b)
{
int res = cmpr(a, b);
if (res == 0) return s[a].substr(pos[a]) + 'Z' > s[b].substr(pos[b]) + 'Z';
else return (res == -1);
}
inline void work()
{
cin >> n;
for (int i = 1; i <= n; i++)
cin >> s[i], m = max(m, (int)s[i].size());
if (m == 1)
{
sort(s + 1, s + 1 + n);
for (int i = 1; i <= n; i++) putchar(s[i][0]);
return dwd;
}
for (int i = 1; i <= n; i++)
{
int len = s[i].size();
for (int j = 1; j <= len; j++)
{
bool flag = 1;
for (int k = j; k < len; k++)
{
if (s[i][k] < s[i][k % j]) { flag = 0; break; }
else if (s[i][k] > s[i][k % j]) { flag = 1; break; }
}
if (flag) { str[i] = s[i].substr(0, j); break; }
}
if (!str[i].size()) str[i] = s[i];
int len2 = str[i].size(), j;
for (j = len2; j < len; j += len2)
if (str[i] != s[i].substr(j, len2)) { pos[i] = j; break; }
if (!pos[i]) pos[i] = j;
}
for (int i = 1; i <= n; i++) Id[i] = i;
sort(Id + 1, Id + 1 + n, cmp);
ansx = s[Id[n]][0];
for (int i = n - 1; i > 0; i--)
{
int j = 1;
tmp = s[Id[i]][0] + ansx;
cpy = tmp;
for (j=j; j < s[Id[i]].size(); j++)
{
tmp = ansx;
for (int k = j; k >= 0; k--) tmp = s[Id[i]][k] + tmp;
if (cpy > tmp) { pre[Id[i]] = j; cpy = tmp; }
}
for (int j = pre[Id[i]]; j >= 0; j--) ansx = s[Id[i]][j] + ansx;
}
cout<<ansx<< "\n";
return dwd;
}
T3
发现贪心地从上往下选的话会被hack,原因是决策时只考虑了当前一层的决策点,而非全局最优,那么很可能会被下面的更优点给替换掉,所以我们考虑换一种策略。
我们考虑从叶子往上一层一层地合并,把我们进出点可以获得正贡献的点合并为一个,然后记录进入这个点的所需要的前提费用与进入子树直到贡献为负时返回的最大贡献,那么显然我们进行完缩点之后剩下的点都是只需要考虑是否进入即可,之后按照进入费用排序,每次贪心地选择一个最小的但是贡献为正的结点然后去获取他能够贡献出来的贡献,再与直接到母矿的路径的前提费用进行比较,如果更小的话就显然可以直接进入从而得到答案了。
using namespace __gnu_pbds;
#define pds __gnu_pbds
#define int long long
#define Maxn 200001
const int inf = 1e18;
int to[Maxn],nxt[Maxn],head[Maxn],ecnt;
inline void add(int u,int v)
{
to[++ecnt]=v;
nxt[ecnt]=head[u];
head[u]=ecnt;
return;
}
struct Node
{
int ned,get;
friend bool operator<(Node a,Node b) { return ((a.ned^b.ned)?(a.ned<b.ned):(a.get>b.get)); }
friend bool operator>(Node a,Node b) { return b<a; }
};
int n;
int val[Maxn],cst[Maxn];
pds::priority_queue<Node,greater<Node>> q[Maxn];
inline void dfs(int x)
{
for(int i=head[x];i;i=nxt[i])
{
int v=to[i];
dfs(v);
q[x].join(q[v]);
}
int Need=cst[x];
int Val=val[x]-cst[x];
while(q[x].size() and (Val<0 or Need>=q[x].top().ned))
{
Node now=q[x].top();
q[x].pop();
if(Need+Val<=now.ned)
Need+=now.ned-(Need+Val);
Val+=now.get;
}
if(Val>0)
q[x].push({Need,Val});
return;
}
inline void work()
{
n=read(),cst[1]=inf;
for(int i=2;i<=n;i++)
{
int fr=read()+1;
val[i]=read(),cst[i]=read();
add(fr,i);
if(val[i]==-1)
val[i]=inf*2;
}
dfs(1);
write(q[1].top().ned-inf);
return dwd;
}
11.9
T1
给定一个树每个点进入的时候会强制让你加上一个点权,一个点可以多次经过。多次询问从点 \(s\) 到 \(t\) 在 \(x\) 的初始代价下能不能到达。
那么我们肯定是希望能直接到就直接到的,所以可以预处理,就快速查询两点之间的最短距离,也就是预处理出来路径上的代价前缀最小值,如果这个值比初始更小的话肯定到不了。
如果不能的话肯定也是希望去找一个能够无限获得正代价的边,那么我们可以用树上DP去预处理出来,每次查询的时候也是和当前初始代价比一下。
当然我们还可以发现第一种情况的前缀最小值肯定是整条路经或者刨掉终点,否则的话路径上就会有无限正代价的点辣。
#define int long long
const int inf = 1e18;
const int Maxn = 1e6+10;
int n,q;
int a[Maxn],dis2[Maxn];
int mini[Maxn];
vector<int> e[Maxn];
bool vis[Maxn];
namespace SP
{
int siz[Maxn],dep[Maxn],son[Maxn],top[Maxn],dis[Maxn],fa[Maxn];
inline void dfs1(int x)
{
siz[x]=1;
dep[x]=dep[fa[x]]+1;
dis[x]=dis[fa[x]]+a[x];
if(a[x]+a[fa[x]]>0) vis[x]=1;
for(auto v:e[x])
{
if(v!=fa[x])
{
fa[v]=x; dfs1(v);
if(a[x]+a[v]>0) vis[x]=1;
siz[x]+=siz[v];
if(siz[v]>siz[son[x]]) son[x]=v;
if(mini[v]>=-inf) mini[x]=max(mini[x],min(a[x],mini[v]+a[x]));
}
}
if(vis[x])
mini[x]=max(mini[x],a[x]),dis2[x]=1;
return;
}
inline void dfs2(int x,int fr)
{
top[x]=fr;
dis2[x]+=dis2[fa[x]];
if(mini[fa[x]]>=-inf) mini[x]=max(mini[x],min(a[x],a[x]+mini[fa[x]]));
if(son[x]) dfs2(son[x],fr);
for(auto v:e[x])
if(v!=fa[x] and v!=son[x])
dfs2(v,v);
}
inline int LCA(int x,int y)
{
while(top[x]!=top[y])
{
if(dep[top[x]]<dep[top[y]])
swap(x,y);
x=fa[top[x]];
}
return dep[x]<dep[y]?x:y;
}
inline int dist(int s,int t,int lca) { return dis[s]+dis[t]-dis[lca]*2+a[lca]; }
}
inline void work()
{
scanf("%lld%lld",&n,&q);
memset(mini,-63,sizeof(mini));
for(int i=1;i<=n;i++) scanf("%lld",&a[i]);
for(int i=1;i<n;i++)
{
int u,v;
scanf("%lld%lld",&u,&v);
e[u].push_back(v);
e[v].push_back(u);
}
SP::dfs1(1); SP::dfs2(1,1);
while(q--)
{
int x,s,t;
scanf("%lld%lld%lld",&x,&s,&t);
int lca=SP::LCA(s,t);
if(mini[s]>=-x)
puts("Yes");
else
{
int d;
int d1=SP::dist(s,t,lca);
if(lca!=t) d=d1;
else d=SP::dis[s]-SP::dis[t];
if(d1>=-x and d>=-x and dis2[s]+dis2[t]-2*dis2[lca]+(int)vis[lca]==0)
puts("Yes");
else
puts("No");
}
}
}
T2
对于一个 \(1,\dots,n\) 的排列 \(a_1,\dots,a_n\),定义 \(i\) 处的顺序对数 \(f(i)\) 为满足 \(1\leq j<i\) 且 \(a_j<a_i\) 的 \(j\) 的数量,定义 \(i\) 处的逆序对数 \(g(i)\) 为满足 \(i<j\leq n\) 且 \(a_j<a_i\) 的 \(j\) 的数量。
给定 \(n\),对于每个 \(k=0,1,\dots,n-1\),求出满足 \(\max_{i=1}^n|f(i)-g(i)|=k\) 的 \(a_1,\dots,a_n\) 的数量模 \(10^9+7\) 的值。
转换一下,我们求出来 \(\le k\) 的贡献,差分一下就是 \(k\) 的答案。
现在想想怎么实现。
那么我们可以把题目更加一般地转换,模拟为从一个空排列开始,从 \(1...n\) 插入到当前排列的某个位置,那么显然这种构造的方法可以考虑到所有的排列。
那么过程中去考虑 \(i+1\) 插入的位置不同所产生的贡献差异。
如果当前 \(i+1\) 插在 \(p,p+1\)(位置)
之间,那么 \(i+1\) 所对应地顺序对数为 \(p\),而逆序对数为 \(i-p\)(因为我们是从小到大插入的)。只需要保证 \(|p-(i-p)|\le k\) 即可。
记插入 \(i+1\) 时满足条件的 \(p\) 的数量为 \(c(i)\),那么可以得到:
于是转化为对每个 \(k\) 算 \(\prod\limits_{i=0}^n c(i)\)。
求完之后差分一下就是 \(\max_{i=1}^n |f(i)-g(i)| = k\) 的答案。
因为发现\(c\)的乘数要么是 \(k\) 要么是 \(k+1\),或者为 \(i+1\),显然直接按照奇偶性可以快速统计出来各个因数的个数,所以对单个 \(k\) 容易 \(O(\log n)\) 计算,总时间复杂度 \(O(n \log n)\)。
const int Maxn = 1e6+10;
const int P = 1e9+7;
int n;
inline int qp(int a,int b)
{
int res=1;
while(b)
{
if(b&1) res=res*a%P;
a=a*a%P,b>>=1;
}
return res;
}
inline void work()
{
n=read();
int lst=0,fac=1;
for(int k=0;k<n;k++,fac=fac*k%P)
{
int p=(n-k)/2;
int ansx=fac*qp(k+1,p+((n-k)&1))%P*qp(k,p)%P;
write((ansx-lst+P)%P);putchar(' ');
lst=ansx;
}
return dwd;
}
T3
现在有一个长度为 \(n\) 的字符串 \(S\) 与一个长度为 \(m\) 的字符串 \(T\)。
定义字符串 \(S_i\) 表示将从 \(S\) 的第 \(i\) 个字符后断开得到 \(A\),\(B\),将 \(B\) 从尾到头形成的字符串设为 \(B'\),将 \(B'\) 接在 \(A\) 后面得到的字符串。
对于每个 \(i\),FAT 想知道 \(T\) 在 \(S_i\) 中出现的次数。
把贡献拆成三部分的,\(A,B'\) 两部分预处理,再加上中间一部分拼接的即可。
那么现在就考虑怎么计算第三种。
发现 \(T\) 的一个后缀与 \(B'\) 前缀匹配,剩余的前缀与 \(A\) 的后缀匹配。
那么可以预处理出来所有和 \(B'\) 的前缀所匹配的 \(T\) 后缀,然后快速询问他们剩余的前缀有多少个是 \(A\) 的后缀。
那么直接失配树。
const int Maxn = 2000100;
char s[Maxn],t[Maxn];
int nxt1[Maxn],nxt2[Maxn];
int lens[Maxn],ansx[Maxn],suf[Maxn];
int dfn1[Maxn],dfn2[Maxn];
int c[Maxn<<1],cnt;
vector<int> e[Maxn],vec;
#define lowbit(x) (x&(-x))
inline void add(int x,int k)
{
while(x<=cnt) c[x]+=k,x+=lowbit(x);
return;
}
inline int ask(int x)
{
int res=0;
while(x) res+=c[x],x-=lowbit(x);
return res;
}
inline void kmp(char s[],int nxt[],int n)
{
nxt[1]=0;
int p=0;
for(int i=2;i<=n;i++)
{
while(p and s[i]!=s[p+1]) p=nxt[p];
if(s[i]==s[p+1]) p++;
nxt[i]=p;
}
return;
}
inline void dfs(int x)
{
dfn1[x]=++cnt;
for(auto v:e[x])
dfs(v);
dfn2[x]=++cnt;
return;
}
int n,m,p=0;
inline void work()
{
scanf("%s%s",s+1,t+1);
n=strlen(s+1),m=strlen(t+1);
kmp(t,nxt1,m);
p=0;
for(int i=1;i<=n;i++)
{
while(p and s[i]!=t[p+1])
p=nxt1[p];
if(s[i]==t[p+1])
p++;
lens[i]=p;
ansx[i]=ansx[i-1];
if(p==m)
p=nxt1[p],ansx[i]++;
}
for(int i=1;i<=m;i++)
e[nxt1[i]].push_back(i);
dfs(0);
reverse(t+1,t+1+m);
kmp(t,nxt2,m);
p=0;
for(int i=1;i<=n;i++)
{
while(p and s[i]!=t[p+1])
p=nxt2[p];
if(s[i]==t[p+1])
p++;
if(p==m)
p=nxt2[p],suf[i-m+1]=1;
}
while(p) vec.push_back(p), p=nxt2[p];
for(int i=n;i>=1;i--)
{
while(vec.size() and i+vec.back()<=n)
{
add(dfn1[m-vec.back()],1);
add(dfn2[m-vec.back()]+1,-1);
vec.pop_back();
}
suf[i]+=suf[i+1];
ansx[i]+=ask(dfn1[lens[i]]);
}
for(int i=1;i<=n;i++)
printf("%d\n",ansx[i]+suf[i+1]);
return dwd;
}
11.10
T1
多组数据,给定 \(n,m,a\) ,求 $ \sum\limits_{i=1}^{n} \sum\limits_{j=1}^{m} [gcd(i,j)\le a]\ lcm(i,j) \pmod {1e9+7}$
\( \sum\limits_{d=1}^{a}\sum\limits_{i=1}^{n/d} \sum\limits_{j=1}^{m/d} d\times i\times j[gcd(i,j)==1] \)
\( \sum\limits{d=1}^{a}\sum\limits_{i=1}^{n/d}\sum\limits_{j=1}^{m/d} d\times i\times j \sum\limits_{k|gcd(i,j)} \mu(k) \)
\( \sum\limits_{d=1}^{a}d\sum\limits_{k=1}\mu(k)k^2S(\lfloor\frac{n}{dk} \rfloor)S(\lfloor\frac{m}{dk} \rfloor) \)
\( \sum\limits_{p=1} S(\lfloor\frac{n}{p}\rfloor)S(\lfloor\frac{m}{p}\rfloor)\sum\limits_{1\le d\le a,d|p}\frac{p^2}{d}\mu(\frac{p}{d}) \)
直接爆蒜!
发现后面一坨是独立的,那么可以考虑整除分块。
对于每一段 $\lfloor\frac{n}{p}\rfloor,\lfloor\frac{m}{p}\rfloor $ 相同的部分分一块。
那么按照询问 \(a\) 从小到大排序,当 \(a\) 增大的时候,只有 \(a|p\) 的 \(p\) 所对应的后面一部分会改变。
直接用树状数组维护即可。
T2
动态维护平面图的连通性问题与连通块个数,同时强制在线,多次操作有删边
平面图转对偶图,发现出现新的连通块当且仅当对偶图上删掉了一个环。
那么直接用并查集维护连通块,处理的时候需要启发式分裂。
#include <bits/stdc++.h>
#define OpTimiSM false
bool Attitude;
using namespace std;
inline int read()
{
int s=0,w=1; char c=getchar();
while(!isdigit(c) and c!=EOF) { if(c=='-') w=-1;c=getchar();}
while(isdigit(c)) { s=s*10+c-'0';c=getchar();}
return s*w;
}
inline void Read(char &c){while((c != '?')and(c != '-')) c = getchar(); return; }
const int Maxn = 1e6 + 5;
#define pr pair<int,int>
int n, q;
int fa[Maxn], t, cnt, lst, t1;
int belong[Maxn], in[Maxn];
vector<int> e[Maxn],vec1, vec2;
map<pr, int> f, id;
map<int, int> mp[Maxn];
map<int, int>::iterator to[Maxn];
inline int find(int x) { return fa[x] == x ? x : fa[x] = find(fa[x]); }
inline bool Push_in(vector<int> &vec, int &p)
{
for (p=p;p<vec.size();p++)
{
auto v=vec[p];
for (auto k = to[v]; k != mp[v].end(); to[v] = ++k)
{
int a = k->first;
if (!in[a])
{
in[a] = 1, vec.push_back(a);
to[a] = mp[a].begin();
return true;
}
}
}
return false;
}
inline void work()
{
n=read(),q=read();
for (int i=1,k;i<=n;i++)
{
k=read();
for (int j=1,x;j<=k;j++)
{ x = read(),e[i].push_back(x); mp[i][x] = 1,id[pr(i, x)] = ++t,fa[t] = t; }
}
for (int i=1;i<=n;i++)
{
int lens=e[i].size();
for (int j = 1; j < lens; j++) fa[find(id[pr(i, e[i][j - 1])])] = find(id[pr(e[i][j], i)]);
fa[find(id[pr(i, e[i].back())])] = find(id[pr(e[i][0], i)]);
}
for (int i=1;i<=n;i++)
{
int l=e[i].size();
for (int j=0;j<l;j++) f[pr(i, e[i][j])] = find(id[pr(i, e[i][j])]);
}
for (int i=1;i<=t;i++) fa[i] = i; cnt=1;
while (q--)
{
char c=getchar(); Read(c);
int x=read()^lst,y=read()^lst;
if (c == '-')
{
int u=f[pr(x, y)],v=f[pr(y, x)];
mp[x].erase(y),mp[y].erase(x);
if (find(u)==find(v))
{
int p1=0,p2=0; cnt++;
vec1.clear(),vec1.push_back(x);
vec2.clear(),vec2.push_back(y);
to[x]=mp[x].begin(),to[y]=mp[y].begin();
while (1)
{
if (!Push_in(vec1, p1)) { t1++; for (auto v:vec1) belong[v] = t1; break; }
if (!Push_in(vec2, p2)) { t1++; for (auto v:vec2) belong[v] = t1; break; }
}
for (auto v:vec1) in[v] = 0; for (auto v:vec2) in[v] = 0;
}
else fa[find(u)] = find(v);
printf("%d\n", lst = cnt);
}
else printf("%d\n", lst = (belong[x] == belong[y]));
}
}
signed main() { do { work(); }while((Attitude=OpTimiSM)); return 0; }
11.14
T1
鸽子位于平面直角坐标系上的点 \((a,b)\),他每次可以朝上下左右走一步但是需要保证坐标非负,鸽子需要走到 \((c,d)\)。每次走的一个新的节 \((x,y)\) 会加上 \([x \& y != 0]\) 的代价。求用最小的代价走回家的贡献。(起点终点贡献不计入)多组数据,\(T \le 1e5,0\le a,b,c,d \le 1e18\)。
打出两两数之间异或值是否为真的表后发现所有 \(0\) 点是连通的,所有 \(1\) 点则构成了直角三角形的谢尔宾斯基三角形,发现最小贡献的话就是走出当前的三角形所花费贡献。
那么就把起点终点走出三角形的贡献加起来即可,但是需要注意到两点位于同一三角形内的情况,需要和直接走取个 \(min\)。
注意到不能直接计算,但是如果位于三角形的左上部分可以快速跳到一个更小的三角形里面计算,而大小不会改变,也就是递归到一个最小的三角形里面去计算贡献。
关于确定点在正方形的左上角还是右下角,可以用 \([x+y>k]\) 判断。注意在三角形内走到边的最小距离为 \(min({x+y-L,L-y-1,L-x-1})\) ,其中 \(L\) 为正方形边长。
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define Cruel false
bool World;
int T;
inline int qp(int a,int b)
{
int res=1;
while(b)
{
if(b&1)
res=res*a;
a=a*a;
b>>=1;
}
return res;
}
inline int gt(int x)
{
return qp(2,floor(log2(x))+1);
}
inline int calc(int x,int y)
{
if((x&y)==0)
return 0;
int res;
while(true)
{
if(x>y)
swap(x,y);
res=gt(y);
if(x+y>=res)
break;
else
y-=res/2;
}
return min({x+y-res,res-y-1,res-x-1});
}
inline void work()
{
T=read();
while(T--)
{
int ansx=0;
int a=read(),b=read(),c=read(),d=read();
if(a==c and b==d)
write(0);
else
write(min((calc(a,b)+calc(c,d)),abs(c-a)+abs(d-b)-1));
putchar('\n');
}
return dwd;
}
signed main()
{
do work();
while((World=Cruel));
return 0;
}
T2
给出多组数据,求字符串里最多出现了多少不相交的子序列为 \(abab\)。
可以转化为找俩 \(ab\) 匹配。考虑去类似贪心地匹配,也就是每个 \(b\) 找到距离最近的 \(a\) 点匹配。
有一种贪心思路是直接将匹配的 \(ab\) 点数量除以 \(2\),但是显然是错误的,可以被形如 \(aabb\) 的数据卡掉。
咋办呢?发现只有这种特殊的构造可以把我们的正确性卡掉,原因是因为出现了交叉的匹配,也就是 \(a\) 跑到了上一个需要撇皮 \(b\) 前面。
那么不能同时选的 \(ab\) 会存在一个位置 \(p\),使得所有 \(a\) 的位置小于 \(p\),\(b\) 的位置则在右。
那么我们在最小化 \(ab\) 相交的最大值的情况下即可构造出答案。
我们设 \(ab\) 相交的最大值最小为 \(mxn\),最多有 \(cnt\) 对 \(ab\),那么答案就为 $ min(\lfloor\frac{cnt}{2}\rfloor,cnt-mxn) $。
也就是说我们的贪心选取方式匹配出来的区间要么是互相包含,要么是互相远离没有相交,而没有一个大区间完全包含另一个小区间的样子。
那么我们可以把类似 \(aab...ba...abb\) 去变成 \(ab...ab\) 和 \(abab\),也就是说把两对都相互包含的互相“中和”一下就可以得到两个 \(abab\)。
也就是说 \(cnt\) 实际上是一个包含的大区间里面有多少需要和外面配对的,我们用外面的去和里面的配对即可。
#include<bits/stdc++.h>
using namespace std;
#define dwd void()
#define Cruel false
bool World;
const int Maxn = 1e7+10;
int T,n,ansx;
int tp,tot;
int st[Maxn],sums[Maxn];
char s[Maxn];
inline void work()
{
ios::sync_with_stdio(0);
cin>>T;
while(T--)
{
cin>>s;
n=strlen(s);
tp=tot=0;
for(int i=0;i<n;i++)
{
if(s[i]=='b')
{
if(tp)
{
sums[i+1]--,sums[st[tp]+1]++;
tp=tp-1,tot=tot+1;
}
}
else
st[++tp]=i;
}
int mxn=0;
for(int i=1;i<=n;i++)
sums[i]+=sums[i-1];
for(int i=1;i<=n;i++)
mxn=max(mxn,sums[i]);
cout<<min(tot/2,tot-mxn)<<"\n";
for(int i=0;i<=n;i++)
sums[i]=0;
}
return dwd;
}
signed main()
{
do work();
while((World=Cruel));
return 0;
}
T3
用 \(0\) 代表空树,如果一个节点没有左子树,那么认为它的左子树是空树(右子树同理)。对任意二叉树 \(A\),\(0\le A\) 成立;对任意非空二叉树 \(A\),\(A\le 0\) 不成立。用 \(ls\) 代表左子树,\(rs\) 代表右子树,则对于非空二叉树 \(A,B\),\(A\le B\) 当且仅当 \(ls(A)\le ls(B)\) 且 \(rs(B)\le rs(A)\)。\(A=B\) 当且仅当 \(A\le B\) 且 \(B\le A\)。否则 \(A\neq B\) 。
给定节点编号为 \(1∼n\) 的二叉树 \(A\)。\(B\) 的初始值为 \(A\)。对 \(B\) 重复进行以下操作:任选 \(B\) 中的一个儿子数量不超过 \(1\) 的节点,为这个节点增加一个儿子(使得 \(B\) 仍然是二叉树)。左右有区别。问共有多少不同(定义见上文) 的 \(B\) 满足 \(B\) 的节点数为 \(n+m\) 且 \(A\le B\)。\(1\le n,m\le 1e6\)
我只能说题意挺抽象。
实际上对于给定形态的树,每个结点的大小关系是确定的,并且很好求。
根节点 \(A\le B\),那么所有点的左子树都和根节点一样,右子树则和根节点相反,直接遍历一遍树就可以求出来哪些点可以放,其中可以放的点是和根节点一个状态的。
那么问题就转化为了 \(c\) 个独立的位置,放 \(m\) 个点形成我们的二叉树森林,询问方案树。
那么显然 \(c=1\) 的时候是卡特兰数,这是个加强版。
那么考虑设 \(f[c][m]\) 为上述式子结构,可得
复杂度 \(n^3\),考虑换个角度。
我们如果第 \(c\) 个位置大于 \(0\),可以拿走根节点,把他分为两个相互独立的位置;如果等于 \(0\),那么可以删去这个位置。所以有
复杂度 \(n^2\)。
再转换一下,把他放在坐标系里,那么就可以转化为路径计数:
当一个点位于 \((x,y)\) 时,下一步可以走到 \((x−1,y+1)\) 或 \((x+1,y)\)。且 \(x>0\)。求 \((1,0)\) 到 \((c,m)\) 的方案数。
把 \((x,y)\) 代换为 \((x+y,y)\),可以得到:
当一个点位于 \((x,y)\) ,下一步可以走到 \((x,y+1)\) 或 \((x+1,y)\)。且 \(x>y\)。求 \((1,0)\) 到 \((c+m,m)\) 的方案数。
我的评价是不做评价,答案为 $ C_{c+2m-1}^{m} - C_{c+2m-1}^{c+m} $。
先不考虑 $ x>y $ 的限制,就是求向上走 $ m $ 步,向右走 $ c+m-1 $ 步的方案数,即 $ C_{c+2m-1}^{m} $ 。然后对于超过直线 $ y=x $ 的路径,关于过其第一次超过直线 \(y=x\) 的点、斜率为 \(1\) 的直线做轴对称,发现路径的终点变成了 \((m,c+m)\) ,方案数为 $ C_{c+2m-1}^{c+n} $。最后答案为 $ C_{c+2m-1}^{m} - C_{c+2m-1}^{c+m} $。
#define Cruel false
bool World;
const int P = 1914270647;
inline int qp(int a,int b)
{
int res=1;
while(b)
{
if(b&1)
res=res*a%P;
a=a*a%P;
b>>=1;
}
return res;
}
const int Maxn = 3e6+10;
int fac[Maxn];
inline void Init(int n)
{
fac[1]=1,fac[0]=1;
for(int i=1;i<=n;i++)
fac[i]=fac[i-1]*i%P;
return;
}
inline int C(int n,int m)
{
if(n<m or m<0)
return 0;
return fac[n]*qp(fac[m],P-2)%P*qp(fac[n-m],P-2)%P;
}
int n,m,c;
int ls[Maxn],rs[Maxn];
unordered_map<int,bool> vis;
inline void dfs(int x,int Type)
{
if(!x)
{
c+=(!(Type));
return;
}
dfs(ls[x],Type);
dfs(rs[x],Type^1);
return;
}
inline void work()
{
Init(Maxn-10);
n=read(),m=read();
for(int i=1;i<=n;i++)
{
ls[i]=read(),rs[i]=read();
vis[ls[i]]=vis[rs[i]]=1;
}
for(int i=1;i<=n;i++)
if(!vis.count(i))
dfs(i,0);
write((C(c+m*2-1,c+m-1)-C(c+m*2-1,c+m)+P)%P);
return dwd;
}
signed main()
{
do work();
while((World=Cruel));
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号