浅谈分块与莫队
块状数组
实际上,分块是一种思想,块状数组仅仅是其实现方式之一
把一个整体划分为若干个小块,对于整块整体处理,零散处仅需要优雅的处理即可
我们首先介绍块状数组,即用分块思想处理区间问题的一种数据结构。
一般来说我们取块长为 $ \sqrt{n} $ 以平衡复杂度,最差情况下仅需处理接近 \(\sqrt{n}\) 个整块,并且需要对长度为 \(\frac{2n}{\sqrt{n}}\) 的零散处进行单独处理,总体复杂度为\(O(\sqrt{n})\),是一种牛逼的根号算法。
显然在一些情况下我们的根号算法比不上对数级算法,但是用巨大的时间所换来的是我们更高的灵活性。块状数组显然维护东西的时候不需要结合律,也不用依靠线段树的递归结构去传递$ tag $。当然了,我们也可以直接把它看做是一颗高度为3的树,不是二叉树
没了。
主要还是去看具体怎么维护一些东西
我们在这里就以Loj上的序列分块入门为例子来浅浅地实现一下
入门1:
观察数据范围显然分块可做
提前预处理出来每个块的左右端点,根据题意模拟。
因为是单点查询,类似于线段树的\(lazytag\),我们也对于每一个块也整一个\(tag\)。这样你就可以在处理整个块的时候直接对于整个块进行加减。
当左右端点没有越过两个块的时候,直接优雅地处理
否则,找到两个端点所在块,于中间的块进行整体处理,对于两边的块依旧优雅地处理。有句话说得好,越简单的算法就越优雅
#include<bits/stdc++.h>
using namespace std;
int n;
int num,len;
int le[50010],re[50010];
int belong[50010];
int tag[51000];
int a[50010];
inline void work1(int l,int r,int c)
{
int p1=belong[l];
int p2=belong[r];
if(p2-p1<=2)
{
for(register int i=l;i<=r;i++)
a[i]+=c;
}
else
{
for(register int i=p1+1;i<=p2-1;i++)
tag[i]+=c;
for(register int i=l;i<=re[p1];i++)
a[i]+=c;
for(register int i=le[p2];i<=r;i++)
a[i]+=c;
}
return ;
}
inline void work2(int r)
{
printf("%d\n",a[r]+tag[belong[r]]);
return ;
}
inline void work()
{
n=read();
num=sqrt(n);
len=(n-1)/num+1;
for(register int i=1;i<=n;i++)
{
a[i]=read();
belong[i]=(i-1)/num+1;
}
le[1]=1; re[1]=num;
for(register int i=2;i<=len;i++)
{
le[i]=re[i-1]+1;
re[i]=le[i]+num-1;
}
for(register int i=1;i<=n;i++)
{
int opt;
int l,r,c;
opt=read();
l=read(); r=read(); c=read();
if(opt==0)
work1(l,r,c);
else
work2(r);
}
return ;
}
int main(void)
{
work();
return 0;
}
入门2:
带修查找区间内小于某个值的元素数量
我们写分块时主要考虑的是修改和查询之间的关系,我们要让所维护的东西尽量去靠拢查询,便于我们处理
因为我们是优雅地解题,所以我们优雅地处理。
对于问题,我们发现这东西不好去简单的维护,那就先想想大力维护。
如果整个序列无序,那么我们只能直接遍历判断。
但是我们是分块。
如果某个块内有序,是否可以更快的得到答案?事实证明可以。
有序之后直接二分可以在\(log\)时间内找到此块的答案。
秉承着这个思路,我们考虑怎么实现修改
我们更改元素后如果是整块地修改那么显然相对大小不变。对于零散块来说,显然这玩意又无序了。咋办呢?再排一遍。
我们可以用vector来帮助我们实现
剩下的预处理啥的和入门1一样,不再阐述
#include<bits/stdc++.h>
using namespace std;
int n;
int Size,len;
int a[50010*2];
int belong[50010*2];
int le[510],ri[510];
int tag[510];
vector<int> v[510];
inline void lnit(int x)
{
v[x].clear();
for(register int i=le[x];i<=ri[x];i++)
v[x].push_back(a[i]);
sort(v[x].begin(),v[x].end());
}
inline void work1(int l,int r,int c)
{
int bl=belong[l],br=belong[r];
for(register int i=l;i<=min(ri[bl],r);i++)
a[i]+=c;
lnit(bl);
for(register int i=bl+1;i<=br-1;i++)
tag[i]+=c;
if(bl!=br)
{
for(register int i=le[br];i<=r;i++)
a[i]+=c;
lnit(br);
}
return;
}
inline void work2(int l,int r,int c)
{
int bl=belong[l],br=belong[r];
int ansx=0; long long mod=c*c;
for(register int i=l;i<=min(ri[bl],r);i++)
{
if(mod>a[i]+tag[bl])
ansx++;
}
for(register int i=bl+1;i<=br-1;i++)
{
ansx+=lower_bound(v[i].begin(),v[i].end(),mod-tag[i])-v[i].begin();
}
if(bl!=br)
{
for(register int i=le[br];i<=r;i++)
{
if(mod>a[i]+tag[br])
ansx++;
}
}
printf("%d\n",ansx);
return;
}
inline void work()
{
n=read();
Size=sqrt(n);
len=(n-1)/Size+1;
for(register int i=1;i<=n;i++)
a[i]=read(),belong[i]=(i-1)/Size+1;
for(register int i=1;i<=n;i++)
v[belong[i]].push_back(a[i]);
for(register int i=1;i<=belong[n];i++)
sort(v[i].begin(),v[i].end());
le[1]=1; ri[1]=Size;
for(register int i=2;i<=len;i++)
{
le[i]=ri[i-1]+1;
ri[i]=le[i]+Size-1;
}
for(register int i=1;i<=n;i++)
{
int opt,l,r,c;
opt=read();
l=read();
r=read();
c=read();
if(opt==0)
work1(l,r,c);
else
work2(l,r,c);
}
return;
}
int main(void)
{
work();
return 0;
}
入门3:
带修找前驱
和上一个题一样,因为都是找小于某个数,同样考虑二分
别的操作都差不多,只不过是你的查找变成了值
直接lower_bound一下找位置就是所求
再给每个块所求的取个max
没了
#include <bits/stdc++.h>
using namespace std;
#define int long long
int n, Size, len;
int a[100010];
int be[100010];
int tag[100010];
int le[101000], ri[100010];
set<int> s[100010];
inline void add(int l, int r, int c)
{
int bl = be[l], br = be[r];
for (register int i = l; i <= min(ri[bl], r); i++)
{
s[bl].erase(a[i]);
a[i] += c;
s[bl].insert(a[i]);
}
if (bl != br)
{
for (register int i = le[br]; i <= r; i++)
{
s[br].erase(a[i]);
a[i] += c;
s[br].insert(a[i]);
}
}
for (register int i = bl + 1; i <= br - 1; i++)
tag[i] += c;
return;
}
inline void ask(int l, int r, int c)
{
int ansx = -1;
int bl = be[l], br = be[r];
for (register int i = l; i <= min(ri[bl], r); i++)
{
int v = a[i] + tag[bl];
if (v < c)
ansx = max(v, ansx);
}
if (bl != br)
{
for (register int i = le[br]; i <= r; i++)
{
int v = a[i] + tag[br];
if (v < c)
ansx = max(ansx, v);
}
}
for (register int i = bl + 1; i <= br - 1; i++)
{
int now = c - tag[i];
set<int>::iterator it = s[i].lower_bound(now);
if (it == s[i].begin())
continue;
--it;
ansx = max(ansx, *it + tag[i]);
}
printf("%d\n", ansx);
return;
}
inline void work()
{
n = read();
Size = sqrt(n);
len = (n - 1) / Size + 1;
for (register int i = 1; i <= n; i++)
{
a[i] = read();
be[i] = (i - 1) / Size + 1;
s[be[i]].insert(a[i]);
}
le[1] = 1;
ri[1] = Size;
for (register int i = 2; i <= len; i++)
{
le[i] = ri[i - 1] + 1;
ri[i] = le[i] + Size - 1;
}
ri[len] = n;
for (register int i = 1; i <= n; i++)
{
int opt;
int l, r, c;
opt = read();
l = read();
r = read();
c = read();
if (opt == 0)
{
add(l, r, c);
}
else
{
ask(l, r, c);
}
}
return;
}
signed main()
{
work();
return 0;
}
入门4:
水
入门5:
区间开方,区间求和
好消息,不带修
所以也是水,直接模拟
是肯定不行的,因为开方慢的一批
我们想想开方的性质,你会发现一个\(2^{32}\)的数开5,6次就会成1
也就是说一个数开几次后就不用开了,因为此时这个数不是1就是0
那么对于这种开方前后没有区别的块就可以跳过
如何判断这种块呢?(智慧核心
整个flag数组表示每个块是否有这种特殊性质
好啦我们节省了很多时间
那么怎么开方呢?
优雅地对于所有数开方即可
所以我们
#include <bits/stdc++.h>
using namespace std;
#define int long long
int n, Size, len;
int a[50010];
int be[50010];
int sums[50100];
int le[50100], ri[50010];
bool flag[5010];
inline void sq(int x)
{
if (flag[x])
return;
flag[x] = 1;
sums[x] = 0;
for (register int i = le[x]; i <= ri[x]; i++)
{
a[i] = sqrt(a[i]);
sums[x] += a[i];
if (a[i] > 1)
flag[x] = 0;
}
return;
}
inline void work1(int l, int r)
{
int bl = be[l], br = be[r];
for (register int i = l; i <= min(ri[bl], r); i++)
{
sums[bl] -= a[i];
a[i] = sqrt(a[i]);
sums[bl] += a[i];
}
if (bl != br)
{
for (register int i = le[br]; i <= r; i++)
{
sums[br] -= a[i];
a[i] = sqrt(a[i]);
sums[br] += a[i];
}
}
for (register int i = bl + 1; i <= br - 1; i++)
sq(i);
return;
}
inline void work2(int l, int r)
{
int bl = be[l], br = be[r];
int ansx = 0;
for (register int i = l; i <= min(ri[bl], r); i++)
{
ansx += a[i];
}
if (bl != br)
{
for (register int i = le[br]; i <= r; i++)
ansx += a[i];
}
for (register int i = bl + 1; i <= br - 1; i++)
{
ansx += sums[i];
}
printf("%d\n", ansx);
return;
}
inline void work()
{
n = read();
Size = sqrt(n);
len = (n - 1) / Size + 1;
for (register int i = 1; i <= n; i++)
{
a[i] = read();
be[i] = (i - 1) / Size + 1;
sums[be[i]] += a[i];
}
le[1] = 1;
ri[1] = Size;
for (register int i = 2; i <= len; i++)
{
le[i] = ri[i - 1] + 1;
ri[i] = le[i] + Size - 1;
}
ri[be[n]] = n;
for (register int i = 1; i <= n; i++)
{
int opt, l, r, c;
opt = read();
l = read();
r = read();
c = read();
if (opt == 0)
{
work1(l, r);
}
else
{
work2(l, r);
}
}
return;
}
signed main()
{
work();
return 0;
}
入门6:
单点插入加单点询问
直接vector即可AC
但是我们想要的不是AC,是如何用分块解决这个问题。
对于插入这个神奇的操作,我们仍然可以去找到插入的位置所属的块的位置
再进行插入
我们会发现在测试数据之中可能会在同一个位置插入很多次,那么当下一次再次处理此块时会耗费很多时间。所以我们借此引出一个全新的操作,当插入的元素到达了一个界限时我们对所有元素重新分块,重构
当然至于“界限”的定义就是各位自己在实际情况中摸索了
#include<bits/stdc++.h>
using namespace std;
const int N=100010;
typedef pair<int,int> PII;
int st[2*N],a[N],block,num,n,m;
vector<int> v[N];
PII query(int x)///返回某个位置是在第几个块的第几个位置
{
int k=1;
while(x > v[k].size())
{
x -= v[k].size(),k++;
}
return make_pair(k,x-1);///v中下标从零开始,即每个块的左边界都是0
}
void build()
{
block=sqrt(n);
num=n/block;if(n%block) num++;
for(int i=1;i<=n;i++)
{
int idx=(i-1)/block+1;
v[idx].push_back(a[i]);
}
}
void rebuild()
{
int s=0;
for(int i=1;i<=num;i++)
{
for(int j=0;j<v[i].size();j++)
{
st[++s]=v[i][j];
}
v[i].clear();
}
int block2=sqrt(s);
num=s/block2; if(s%block2) num++;
for(int i=1;i<=s;i++)
{
int idx=(i-1)/block+1;
v[idx].push_back(a[i]);
}
}
void insert(int x,int c)
{
PII tmp=quary(x);
v[tmp.first].insert(v[tmp.first].begin()+tmp.second,c);
if(v[tmp.first].size()>20*block) rebuild();
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
}
build();
m=n;
while(m--)
{
int op,l,r,c;
scanf("%d%d%d%d",&op,&l,&r,&c);
if(op==0) insert(l,r);
else{
PII it=query(r);
printf("%d\n",v[it.first][it.second]);
}
}
return 0;
}
\({显然这不是我的马蜂,原因不好解释}~~\)
入门7:
显然,水题
入门8:
显然,我们可以用ODT
显然,我们要用分块
直接维护一个flag数组一个num数组,分别表示整个块内元素是否全部相同,num表示如果相同的话那个元素是谁
没了,优雅即可
#include <bits/stdc++.h>
using namespace std;
#define int long long
int n, Size, len;
int belong[100010];
int tag[100010];
int le[1010], ri[1010];
int a[100010];
int t[100100];
inline void reset(int x)
{
if (tag[x] == -1)
return;
for (register int i = le[x]; i <= ri[x]; i++)
{
a[i] = tag[x];
}
tag[x] = -1;
}
inline void works(int l, int r, int c)
{
int bl = belong[l], br = belong[r];
int ansx = 0;
reset(bl);
for (register int i = l; i <= min(ri[bl], r); i++)
{
if (a[i] != c)
a[i] = c;
else
ansx++;
}
if (bl != br)
{
reset(br);
for (register int i = le[br]; i <= r; i++)
{
if (a[i] != c)
a[i] = c;
else
ansx++;
}
}
for (register int i = bl + 1; i <= br - 1; i++)
{
if (tag[i] != -1)
{
if (tag[i] != c)
tag[i] = c;
else
ansx += Size;
}
else
{
for (register int j = le[i]; j <= ri[i]; j++)
{
if (a[j] != c)
a[j] = c;
else
ansx++;
tag[i] = c;
}
}
}
printf("%lld\n", ansx);
return;
}
inline void work()
{
memset(tag, -1, sizeof(tag));
n = read();
Size = sqrt(n);
for (register int i = 1; i <= n; i++)
{
a[i] = read();
belong[i] = (i - 1) / Size + 1;
}
le[1] = 1;
ri[1] = Size;
len = belong[n];
for (register int i = 2; i <= len; i++)
{
le[i] = ri[i - 1] + 1;
ri[i] = le[i] + Size - 1;
}
ri[len] = n;
for (register int i = 1; i <= n; i++)
{
int l, r, c;
l = read();
r = read();
c = read();
works(l, r, c);
}
return;
}
signed main()
{
work();
return 0;
}
分块9:
经典老题,找区间最小众数
但是它没有强制在线
那么我们显然直接莫队即可
蒲公英我相信大家都会
分块入门9题结束了,这也确实是非常非常基础的几个分块题,主要是帮助大家理解分块的思想
你们的任务就是写P4135和P2464,当然是下节课写
俩淼题
莫队
普通
一般来说的话序列问题莫队都能做,就是可以解决不强制要求在线的区间问题
,只是看数据范围决定你能拿多少分。
比较常见的类型有普通莫队,带修莫队,回滚莫队和树上莫队等。
普通的莫队主要优化就是对于询问的排序来让其左右指针的移动尽量少来降低复杂度——
假设我们有俩指针\(l\)和\(r\),第\(i\)个需要修改的区间是\([L,R]\),那么按照最暴力的思想来算,我们要把\(l\)移动到\(L\),\(r\)移动到\(R\),同时统计指针移动所带来的影响。那么每次转移的复杂度是\(O(1)\),但是指针最坏情况下是\(O(nm)\)去遍历。
考虑优化,我们发现暴力复杂度的消耗就是移动指针,所以我们运用分块的思想去把询问都离线,我们只希望左指针尽量只向右移动而不回头,右指针作为第二关键字去考虑尽量少向左移动。
那么我们把序列分块,按照左端点所在块为第一关键字,右端点为第二关键字,平衡复杂度之后可以做到\(O(n\sqrt{n})\)的优秀复杂度。
这就是莫队的基本思想,当然我们注意到复杂度还会由每次转移的常数决定,所以我们尽量要在\(O(1)\)的时间内去完成\(add\)与\(del\)操作。
by the way,左指针初值赋值应为\(1\),右指针则直接赋\(0\)。因为左指针也是\(0\)的话可能会导致重复计算数值为\(0\)的情况。
带修
当然很多情况下你的问题是带修的,普通的莫队因为需要离线去处理所以很难维护修改。所以我们要给他改造一下来获得更多的暴力分。
我们考虑于普通莫队之上新增一个\(k\)指针去代表时间戳,表示当前的区间是经历了\(k\)次修改之后的状态。
我们每次给询问都记录一个他的时间戳即它当前经历了几次修改,在每次查询的时候只有当前的区间与\(l,r,k\)全部重合才是所求答案
当然了因为多维护了一个指针所以莫队复杂度会严重退化,具体解决方法就是把块长调为神奇的\(n^{\frac{2}{3}}\),可以由神奇的不等式证明,这里不再阐述
因为是在\(n\)和\(m\)同阶的情况下会有这么一个式子
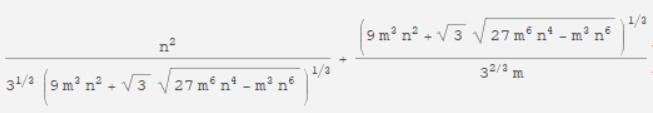
调完之后复杂度最优为\(O(n^{\frac{5}{3}})\)。
回滚
也叫不删除莫队
在处理实际问题的时候你会发现一些情况下你的\(add\)或者\(del\)函数有一个很难实现(如果都不会的话就别用莫队了),那么我们就需要考虑去维护一个操作,再通过更加合理的排序去暴力撤销每个操作的贡献
假设\(add\)很简单,那么我们考虑把删除去掉,而改成增加操作来维护。
首先我们把左端点所属块为第一关键字,右端点为第二关键字,排序之后可以把\(r\)赋值成当前块的结尾,\(l\)则赋值成下一个块的开头。那么对于每次询问,如果\(r\)在当前询问的右端点的左端,那么把右端点去右移。由于这些询问的左端点都在一个块里同时按照右端点升序排序,所以可以直接沿用前面的\(r\)。更新之后保存下来答案为\(k\)。
如果 (l) 指针在当前询问的左端点的右端,那么我们把 (l) 指针左移到当前询问的左端点并更新答案。此时这个询问的答案已经被求出。我们还需要把左端点的影响删除,并且把左端点还原到下一个块的开头。原因是:同一个块内的左端点不一定按照升序排列,如果我们沿用之前的信息,很有可能会处理到不在询问范围内的位置。例如我们先处理了区间 ([3, 5]),再处理了区间 ([4, 6]) 。此时若沿用区间 ([3, 5]) 的信息,我们就会考虑到位置 (3) 的影响,而 (3) 并不在我们查询的区间 ([4, 6]) 内。
特殊情况是某个询问的左端点和右端点在同一个块内,此时暴力做法的时间复杂度不超过 (O(\sqrt{n})) ,直接暴力即可。注意莫队和暴力的信息需要分开存储。
如果 \(l\) 指针在当前询问的左端点的右端,那么我们把 \(l\) 指针左移到当前询问的左端点并更新答案。此时这个询问的答案已经被求出。我们还需要把左端点的影响删除,并且把左端点还原到下一个块的开头。原因是:同一个块内的左端点不一定按照升序排列,如果我们沿用之前的信息,很有可能会处理到不在询问范围内的位置。例如我们先处理了区间 \([3, 5]\),再处理了区间 \([4, 6]\) 。此时若沿用区间 \([3, 5]\) 的信息,我们就会考虑到位置 \(3\) 的影响,而 \(3\) 并不在我们查询的区间 \([4, 6]\) 内。
没了。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号