[从头学数学] 第173节 圆与方程
剧情提要:
[机器小伟]在[project师阿伟]的陪同下进入了结丹初期的修炼。
这次要修炼的目标是[圆与方程]。

知道了能够做些什么呢?
小伟把求DEF的过程炼制成了工具,来玩玩吧:
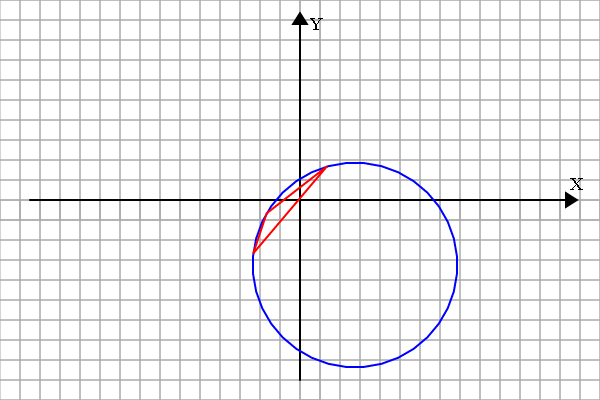
至于交点坐标倒底是什么,就要另外去求了。
本节到此结束。欲知后事怎样。请看下回分解。
[机器小伟]在[project师阿伟]的陪同下进入了结丹初期的修炼。
这次要修炼的目标是[圆与方程]。
正剧開始:
星历2016年04月11日 15:56:41, 银河系厄尔斯星球中华帝国江南行省。
[project师阿伟]正在和[机器小伟]一起研究[圆与方程]。
已知圆心位置和半径来画圆,小伟用36边的多边形取代圆,
面积上略微小了一点。
<span style="font-size:18px;">if (1) {
var r = 20;
config.setSector(1,1,1,1);
config.graphPaper2D(0, 0, r);
config.axis2D(0, 0, 180);
var transform = new Transform();
var a = 5, b = 5, r0 = 5;
var array = shape.nEdge(a, b, r0, 36);
var scale = r;
//array = shape.angularSort(array);
shape.areaDraw(transform.translate(array, -200/scale, -200/scale), 'red', scale);
shape.strokeDraw([].concat(array), 'orange', scale);
}
>>> 3.14*25
78.5</span>
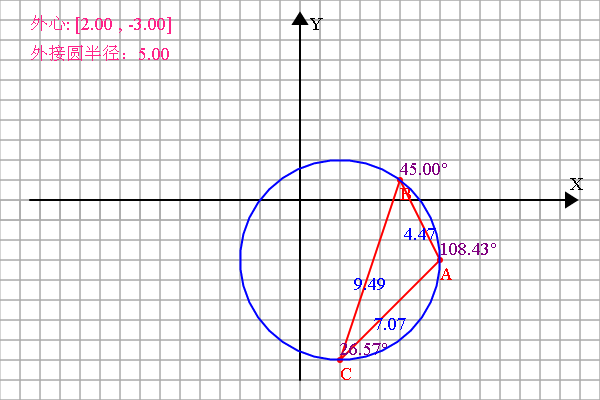
知道三个坐标求外接圆的方程,是这样求的:
<span style="font-size:18px;"> if (1) {
//求三角形的外心
var r = 20;
var r0 = 5*r;
config.setSector(1,1,1,1);
config.graphPaper2D(0, 0, r);
config.axis2D(0, 0, 180);
var triangle = new Triangle();
var transform = new Transform();
//已知三角形顶点阵列
var array = [[5, 1], [7, -3], [2, -8]];
//进行缩放转换
// array = transform.scale(array, r);
//三个顶点
var x1 = array[0][0], y1 = array[0][1],
x2 = array[1][0], y2 = array[1][1],
x3 = array[2][0], y3 = array[2][1];
//令
var A1 = 2*(x2-x1), B1 = 2*(y2-y1), C1 = x2*x2+y2*y2-x1*x1-y1*y1,
A2 = 2*(x3-x2), B2 = 2*(y3-y2), C2 = x3*x3+y3*y3-x2*x2-y2*y2;
//得到外心的坐标
var px = ((C1*B2)-(C2*B1))/((A1*B2)-(A2*B1)),
py = ((A1*C2)-(A2*C1))/((A1*B2)-(A2*B1));
//外接圆半径
var a = distance2D(array[0], array[1]),
b = distance2D(array[1], array[2]),
c = distance2D(array[2], array[0]);
var rOut = a*b*c/Math.sqrt(4*b*b*c*c-Math.pow((b*b+c*c-a*a), 2));
//document.write(px.toFixed(2)+', '+py.toFixed(2)+'; ' + rOut.toFixed(2));
var scale = r;
shape.angleDraw([].concat(array), 'red', scale);
var circle = shape.nEdge(px, py, rOut, 36);
shape.strokeDraw([].concat(circle), 'blue', scale);
var s = '外心: ['+px.toFixed(2)+' , ' + py.toFixed(2)+'] ';
var s1 = '外接圆半径:'+rOut.toFixed(2);
plot.setFillStyle('#FF2288');
plot.fillText(s, -270, -170, 300);
plot.fillText(s1, -270, -140, 300);
}
//二维坐标中两点之间的距离
function distance2D(pointA, pointB) {
return Math.sqrt(Math.pow(pointA[0]-pointB[0], 2)+Math.pow(pointA[1]-pointB[1], 2));
}
</span>
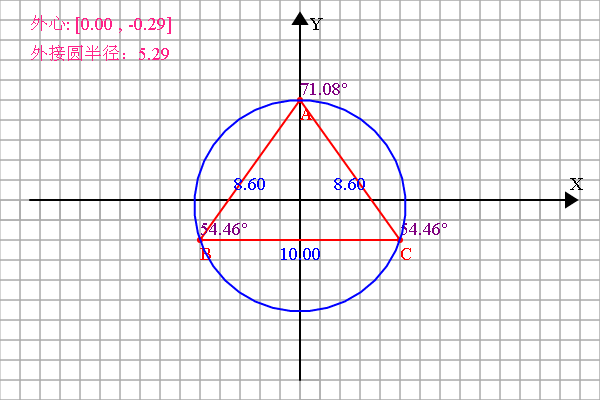
再来试一个:
<span style="font-size:18px;"> //已知三角形顶点阵列
var array = [[-5, -2], [5, -2], [0, 5]]; </span>这个还是比較好玩的。
圆的一般方程:
<span style="font-size:18px;">//圆的一般方程
function generalCircle(D, E, F) {
//方程x^2+y^2+Dx+Ey+F=0;
var rSquare = (D*D+E*E-4*F)/4;
if (rSquare > 0) {
return shape.nEdge(-D/2, -E/2, Math.sqrt(rSquare), 36);
}
else {
return [];
}
}
//直线的一般方程
function generalLine(A, B, C) {
//方程Ax+By+C = 0;
return [[-100, (-100*A+C)/(-B)], [100, (100*A+C)/(-B)]];
}</span>知道了能够做些什么呢?
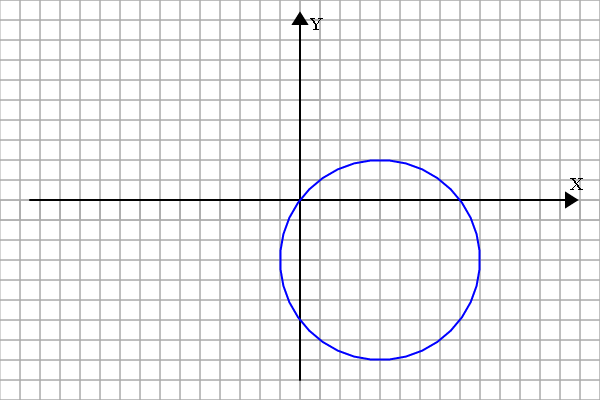
假设如今已经知道了D、E、F的值:
<span style="font-size:18px;"> if (1) {
var r = 20;
config.setSector(1,1,1,1);
config.graphPaper2D(0, 0, r);
config.axis2D(0, 0, 180);
var scale = r;
var circle = generalCircle(-8, 6, 0);
shape.strokeDraw([].concat(circle), 'blue', scale);
}</span>
这就是过那三个点的圆。
D、E、F能够这样来求:
<span style="font-size:18px;"> if (1) {
//运用行列式解线性方程组
var matrix = new Matrix();
var matrixArray = new Array();
var rowArray = new Array();
var ma, mb, mc;
//求过三点的圆的方程
//[x1, y1], [x2, y2], [x3, y3]
// ==> 方程x^2+y^2+Dx+Ey+F=0;
//解D, E, F
var point = [[0,0],[1,1],[4,2]];
var x1 = point[0][0], y1 = point[0][1],
x2 = point[1][0], y2 = point[1][1],
x3 = point[2][0], y3 = point[2][1];
//三元一次方程组[[A1,B1,C1], [A2,B2,C2], ...]
var a = [
[x1, y1, 1, x1*x1+y1*y1],
[x2, y2, 1, x2*x2+y2*y2],
[x3, y3, 1, x3*x3+y3*y3]
];
//三阶
var rank = 3;
for (var i = 0; i < rank; i++) {
matrixArray.push([a[i][0], a[i][1], a[i][2]]);
}
ma = matrix.deepCopy(matrixArray);
for (var i = 0; i < rank; i++) {
ma[i][0] = -a[i][3];
}
mb = matrix.deepCopy(matrixArray);
for (var i = 0; i < rank; i++) {
mb[i][1] = -a[i][3];
}
mc = matrix.deepCopy(matrixArray);
for (var i = 0; i < rank; i++) {
mc[i][2] = -a[i][3];
}
var d, da, db, dc;
d = matrix.delta(matrixArray);
da = matrix.delta(ma);
db = matrix.delta(mb);
dc = matrix.delta(mc);
matrix.print(matrixArray);
document.write('d = ' + d+'<br/>');
matrix.print(ma);
document.write('da = ' + da+'<br/>');
matrix.print(mb);
document.write('db = '+db+'<br/>');
matrix.print(mc);
document.write('dc = '+dc+'<br/>');
var s = 'D = da/d = '+ (da/d).toFixed(2)+', E = db/d = '+(db/d).toFixed(2)
+', F = dc/d = '+(dc/d).toFixed(2);
document.write(s+'<br/>');
}
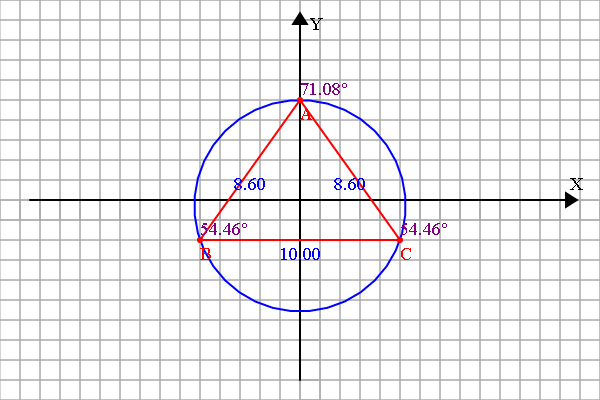
</span>小伟把求DEF的过程炼制成了工具,来玩玩吧:
<span style="font-size:18px;">//求解圆的一般方程中的D、E、F三个系数
//传入的是三个点的坐标阵列
//传回[D, E, F];
function solveDEF(point) {
//运用行列式解线性方程组
var matrix = new Matrix();
var matrixArray = new Array();
var rowArray = new Array();
var ma, mb, mc;
//求过三点的圆的方程
//[x1, y1], [x2, y2], [x3, y3]
// ==> 方程x^2+y^2+Dx+Ey+F=0;
//解D, E, F
//var point = [[0,0],[1,1],[4,2]];
var x1 = point[0][0], y1 = point[0][1],
x2 = point[1][0], y2 = point[1][1],
x3 = point[2][0], y3 = point[2][1];
//三元一次方程组[[A1,B1,C1], [A2,B2,C2], ...]
var a = [
[x1, y1, 1, x1*x1+y1*y1],
[x2, y2, 1, x2*x2+y2*y2],
[x3, y3, 1, x3*x3+y3*y3]
];
//三阶
var rank = 3;
for (var i = 0; i < rank; i++) {
matrixArray.push([a[i][0], a[i][1], a[i][2]]);
}
ma = matrix.deepCopy(matrixArray);
for (var i = 0; i < rank; i++) {
ma[i][0] = -a[i][3];
}
mb = matrix.deepCopy(matrixArray);
for (var i = 0; i < rank; i++) {
mb[i][1] = -a[i][3];
}
mc = matrix.deepCopy(matrixArray);
for (var i = 0; i < rank; i++) {
mc[i][2] = -a[i][3];
}
var d, da, db, dc;
d = matrix.delta(matrixArray);
da = matrix.delta(ma);
db = matrix.delta(mb);
dc = matrix.delta(mc);
return [da/d, db/d, dc/d];
/*
matrix.print(matrixArray);
document.write('d = ' + d+'<br/>');
matrix.print(ma);
document.write('da = ' + da+'<br/>');
matrix.print(mb);
document.write('db = '+db+'<br/>');
matrix.print(mc);
document.write('dc = '+dc+'<br/>');
var s = 'D = da/d = '+ (da/d).toFixed(2)+', E = db/d = '+(db/d).toFixed(2)
+', F = dc/d = '+(dc/d).toFixed(2);
document.write(s+'<br/>'); */
}
</span><span style="font-size:18px;"> if (1) {
var r = 20;
config.setSector(1,1,1,1);
config.graphPaper2D(0, 0, r);
config.axis2D(0, 0, 180);
var array = [[-5, -2], [5, -2], [0, 5]];
var DEF = solveDEF(array);
var scale = r;
var circle = generalCircle(DEF[0], DEF[1], DEF[2]);
shape.strokeDraw([].concat(circle), 'blue', scale);
shape.angleDraw([].concat(array), 'red', scale);
}
</span>
过A。 B, C三个点的圆,没错吧。
再玩一局:
<span style="font-size:18px;">var array = [[-5, -2], [-7, -8], [4, 5]]; </span>
这三个点是偏安一方啊。
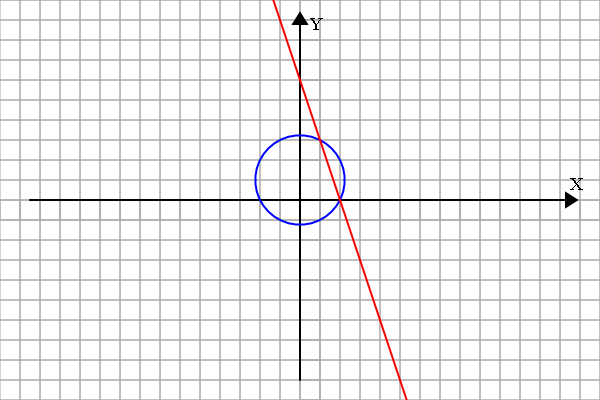
直线和圆的位置关系:
<span style="font-size:18px;"> if (1) {
var r = 20;
config.setSector(1,1,1,1);
config.graphPaper2D(0, 0, r);
config.axis2D(0, 0, 180);
var scale = r;
var circle = generalCircle(0, -2, -4);
var line = generalLine(3, 1, -6);
shape.strokeDraw([].concat(circle), 'blue', scale);
shape.multiLineDraw([].concat(line), 'red', scale);
}</span>
这两个圆的位置关系:
<span style="font-size:18px;"> if (1) {
var r = 20;
config.setSector(1,1,1,1);
config.graphPaper2D(0, 0, r);
config.axis2D(0, 0, 180);
var scale = r;
var circle_1 = generalCircle(2,8,-8),
circle_2 = generalCircle(-4, -4,-2);
shape.strokeDraw([].concat(circle_1), 'blue', scale);
shape.strokeDraw([].concat(circle_2), 'red', scale);
}</span>至于交点坐标倒底是什么,就要另外去求了。
图上看好像是[-1,1] 和[3, -1],也不知对不正确。
[人叫板老师]也没有给出交点坐标。
这里(1.75-1.25)/(1.75+1.25) = 1/6。而1.75+1.25又恰好是PQ距离的一半。
算了,这样的规律没什么意思,直接化简得了。
<span style="font-size:18px;">//二维坐标中两点之间的距离
function distance2D(pointA, pointB) {
return Math.sqrt(Math.pow(pointA[0]-pointB[0], 2)+Math.pow(pointA[1]-pointB[1], 2));
}
//圆的一般方程
function generalCircle(D, E, F) {
//方程x^2+y^2+Dx+Ey+F=0;
var rSquare = (D*D+E*E-4*F)/4;
if (rSquare > 0) {
return shape.nEdge(-D/2, -E/2, Math.sqrt(rSquare), 36);
}
else {
return [];
}
}
//直线的一般方程
function generalLine(A, B, C) {
//方程Ax+By+C = 0;
return [[-100, (-100*A+C)/(-B)], [100, (100*A+C)/(-B)]];
}
//求解圆的一般方程中的D、E、F三个系数
//传入的是三个点的坐标阵列
//传回[D, E, F];
function solveDEF(point) {
//运用行列式解线性方程组
var matrix = new Matrix();
var matrixArray = new Array();
var rowArray = new Array();
var ma, mb, mc;
//求过三点的圆的方程
//[x1, y1], [x2, y2], [x3, y3]
// ==> 方程x^2+y^2+Dx+Ey+F=0;
//解D, E, F
//var point = [[0,0],[1,1],[4,2]];
var x1 = point[0][0], y1 = point[0][1],
x2 = point[1][0], y2 = point[1][1],
x3 = point[2][0], y3 = point[2][1];
//三元一次方程组[[A1,B1,C1], [A2,B2,C2], ...]
var a = [
[x1, y1, 1, x1*x1+y1*y1],
[x2, y2, 1, x2*x2+y2*y2],
[x3, y3, 1, x3*x3+y3*y3]
];
//三阶
var rank = 3;
for (var i = 0; i < rank; i++) {
matrixArray.push([a[i][0], a[i][1], a[i][2]]);
}
ma = matrix.deepCopy(matrixArray);
for (var i = 0; i < rank; i++) {
ma[i][0] = -a[i][3];
}
mb = matrix.deepCopy(matrixArray);
for (var i = 0; i < rank; i++) {
mb[i][1] = -a[i][3];
}
mc = matrix.deepCopy(matrixArray);
for (var i = 0; i < rank; i++) {
mc[i][2] = -a[i][3];
}
var d, da, db, dc;
d = matrix.delta(matrixArray);
da = matrix.delta(ma);
db = matrix.delta(mb);
dc = matrix.delta(mc);
return [da/d, db/d, dc/d];
/*
matrix.print(matrixArray);
document.write('d = ' + d+'<br/>');
matrix.print(ma);
document.write('da = ' + da+'<br/>');
matrix.print(mb);
document.write('db = '+db+'<br/>');
matrix.print(mc);
document.write('dc = '+dc+'<br/>');
var s = 'D = da/d = '+ (da/d).toFixed(2)+', E = db/d = '+(db/d).toFixed(2)
+', F = dc/d = '+(dc/d).toFixed(2);
document.write(s+'<br/>'); */
}
</span>本节到此结束。欲知后事怎样。请看下回分解。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号