int BFMatch(char *s,char *p)
{
int i,j;
i=0;
while(i<strlen(s))
{
j=0;
while(s[i]==p[j]&&j<strlen(p))
{
i++;
j++;
}
if(j==strlen(p))
return i-strlen(p);
i=i-j+1; //指针i回溯
}
return -1;
}int KMPMatch(char *s,char *p)
{
int next[100];
int i,j;
i=0;
j=0;
getNext(p,next);
while(i<strlen(s))
{
if(j==-1||s[i]==p[j])
{
i++;
j++;
}
else
{
j=next[j]; //消除了指针i的回溯
}
if(j==strlen(p))
return i-strlen(p);
}
return -1;
}void getNext(char *p,int *next)
{
int j,k;
next[0]=-1;
j=0;
k=-1;
while(j<strlen(p)-1)
{
if(k==-1||p[j]==p[k]) //匹配的情况下,p[j]==p[k]
{
j++;
k++;
next[j]=k;
}
else //p[j]!=p[k]
k=next[k];
}
}
2.直接求解方法(基本不用)
void getNext(char *p,int *next)
{
int i,j,temp;
for(i=0;i<strlen(p);i++)
{
if(i==0)
{
next[i]=-1; //next[0]=-1
}
else if(i==1)
{
next[i]=0; //next[1]=0
}
else
{
temp=i-1;
for(j=temp;j>0;j--)
{
if(equals(p,i,j))
{
next[i]=j; //找到最大的k值
break;
}
}
if(j==0)
next[i]=0;
}
}
}
bool equals(char *p,int i,int j) //判断p[0...j-1]与p[i-j...i-1]是否相等
{
int k=0;
int s=i-j;
for(;k<=j-1&&s<=i-1;k++,s++)
{
if(p[k]!=p[s])
return false;
}
return true;
}
我们在一个母字符串中查找一个子字符串有很多方法。KMP是一种最常见的改进算法,它可以在匹配过程中失配的情况下,有效地多往后面跳几个字符,加快匹配速度。
当然我们可以看到这个算法针对的是子串有对称属性,如果有对称属性,那么就需要向前查找是否有可以再次匹配的内容。
在KMP算法中有个数组,叫做前缀数组,也有的叫next数组,每一个子串有一个固定的next数组,它记录着字符串匹配过程中失配情况下可以向前多跳几个字符,当然它描述的也是子串的对称程度,程度越高,值越大,当然之前可能出现再匹配的机会就更大。
这个next数组的求法是KMP算法的关键,但不是很好理解,我在这里用通俗的话解释一下,看到别的地方到处是数学公式推导,看得都蛋疼,这个篇文章仅贡献给不喜欢看数学公式又想理解KMP算法的同学。
1、用一个例子来解释,下面是一个子串的next数组的值,可以看到这个子串的对称程度很高,所以next值都比较大。
|
位置i |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
前缀next[i] |
0 |
0 |
0 |
0 |
1 |
2 |
3 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
4 |
0 |
|
子串 |
a |
g |
c |
t |
a |
g |
c |
a |
g |
c |
t |
a |
g |
c |
t |
g |
申明一下:下面说的对称不是中心对称,而是中心字符块对称,比如不是abccba,而是abcabc这种对称。
(1)逐个查找对称串。
这个很简单,我们只要循环遍历这个子串,分别看前1个字符,前2个字符,3个... i个 最后到15个。
第1个a无对称,所以对称程度0
前两个ag无对称,所以也是0
依次类推前面0-4都一样是0
前5个agcta,可以看到这个串有一个a相等,所以对称程度为1前6个agctag,看得到ag和ag对成,对称程度为2
这里要注意了,想是这样想,编程怎么实现呢?
只要按照下面的规则:
a、当前面字符的前一个字符的对称程度为0的时候,只要将当前字符与子串第一个字符进行比较。这个很好理解啊,前面都是0,说明都不对称了,如果多加了一个字符,要对称的话最多是当前的和第一个对称。比如agcta这个里面t的是0,那么后面的a的对称程度只需要看它是不是等于第一个字符a了。
b、按照这个推理,我们就可以总结一个规律,不仅前面是0呀,如果前面一个字符的next值是1,那么我们就把当前字符与子串第二个字符进行比较,因为前面的是1,说明前面的字符已经和第一个相等了,如果这个又与第二个相等了,说明对称程度就是2了。有两个字符对称了。比如上面agctag,倒数第二个a的next是1,说明它和第一个a对称了,接着我们就把最后一个g与第二个g比较,又相等,自然对称成都就累加了,就是2了。
c、按照上面的推理,如果一直相等,就一直累加,可以一直推啊,推到这里应该一点难度都没有吧,如果你觉得有难度说明我写的太失败了。
当然不可能会那么顺利让我们一直对称下去,如果遇到下一个不相等了,那么说明不能继承前面的对称性了,这种情况只能说明没有那么多对称了,但是不能说明一点对称性都没有,所以遇到这种情况就要重新来考虑,这个也是难点所在。
(2)回头来找对称性
这里已经不能继承前面了,但是还是找对称成都嘛,最愚蠢的做法大不了写一个子函数,查找这个字符串的最大对称程度,怎么写方法很多吧,比如查找出所有的当前字符串,然后向前走,看是否一直相等,最后走到子串开头,当然这个是最蠢的,我们一般看到的KMP都是优化过的,因为这个串是有规律的。
在这里依然用上面表中一段来举个例子:
位置i=0到14如下,我加的括号只是用来说明问题:
(a g c t a g c )( a g c t a g c) t
我们可以看到这段,最后这个t之前的对称程度分别是:1,2,3,4,5,6,7,倒数第二个c往前看有7个字符对称,所以对称为7。但是到最后这个t就没有继承前面的对称程度next值,所以这个t的对称性就要重新来求。
这里首要要申明几个事实
1、t 如果要存在对称性,那么对称程度肯定比前面这个c 的对称程度小,所以要找个更小的对称,这个不用解释了吧,如果大那么t就继承前面的对称性了。
2、要找更小的对称,必然在对称内部还存在子对称,而且这个t必须紧接着在子对称之后。
如下图说明。
从上面的理论我们就能得到下面的前缀next数组的求解算法。
void SetPrefix(const char *Pattern, int prefix[])
{
int len=CharLen(Pattern);//模式字符串长度。
prefix[0]=0;
for(int i=1; i<len; i++)
{
int k=prefix[i-1];
//不断递归判断是否存在子对称,k=0说明不再有子对称,Pattern[i] != Pattern[k]说明虽然对称,但是对称后面的值和当前的字符值不相等,所以继续递推
while( Pattern[i] != Pattern[k] && k!=0 )
k=prefix[k-1]; //继续递归
if( Pattern[i] == Pattern[k])//找到了这个子对称,或者是直接继承了前面的对称性,这两种都在前面的基础上++
prefix[i]=k+1;
else
prefix[i]=0; //如果遍历了所有子对称都无效,说明这个新字符不具有对称性,清0
}
}
通过这个说明,估计能够理解KMP的next求法原理了,剩下的就很简单了。我自己也有点晕了,实在不喜欢那些数学公式,所以用形象逻辑思维方法总结了一下。
////////
KMP还有一种写法:这个写法是经过N个人优化的:
1 int j = -1, i = 0; 2 next[0] = -1; 3 while(i < len) 4 { 5 if(j == -1 || ss[i] == ss[j]) 6 { 7 8 i++; 9 j++; 10 next[i] = j; 11 } 12 else 13 { 14 j = next[j]; 15 } 16 }
关于KMP网友的另外解释:
KMP算法,是由Knuth,Morris,Pratt共同提出的模式匹配算法,其对于任何模式和目标序列,都可以在线性时间内完成匹配查找,而不会发生退化,是一个非常优秀的模式匹配算法。但是相较于其他模式匹配算法,该算法晦涩难懂,第一次接触该算法的读者往往会看得一头雾水,主要原因是KMP算法在构造跳转表next过程中进行了多个层面的优化和抽象,使得KMP算法进行模式匹配的原理显得不那么直白。本文希望能够深入KMP算法,将该算法的各个细节彻底讲透,扫除读者对该算法的困扰。
KMP算法对于朴素匹配算法的改进是引入了一个跳转表next[]。以模式字符串abcabcacab为例,其跳转表为:
| j | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| pattern[j] | a | b | c | a | b | c | a | c | a | b |
| next[j] | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 5 | 0 | 1 |
举例说明,如下是使用上例的模式串对目标串执行匹配的步骤
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| b | a | b | c | b | a | b | c | a | b | c | a | a | b | c | a | b | c | a | b | c | a | c | a | b | c |
| a | b | c | a | b | c | a | c | a | b | ||||||||||||||||
| a | b | c | a | b | c | a | c | a | b | ||||||||||||||||
| a | b | c | a | b | c | a | c | a | b | ||||||||||||||||
| a | b | c | a | b | c | a | c | a | b | ||||||||||||||||
| a | b | c | a | b | c | a | c | a | b | ||||||||||||||||
| a | b | c | a | b | c | a | c | a | b |
next跳转表,在进行模式匹配,实现模式串向后移动的过程中,发挥了重要作用。这个表看似神奇,实际从原理上讲并不复杂,对于模式串而言,其前缀字符串,有可能也是模式串中的非前缀子串,这个问题我称之为前缀包含问题。以模式串abcabcacab为例,其前缀4 abca,正好也是模式串的一个子串abc(abca)cab,所以当目标串与模式串执行匹配的过程中,如果直到第8个字符才匹配失败,同时也意味着目标串当前字符之前的4个字符,与模式串的前4个字符是相同的,所以当模式串向后移动的时候,可以直接将模式串的第5个字符与当前字符对齐,执行比较,这样就实现了模式串一次性向前跳跃多个字符。所以next表的关键就是解决模式串的前缀包含。当然为了保证程序的正确性,对于next表的值,还有一些限制条件,后面会逐一说明。
如何以较小的代价计算KMP算法中所用到的跳转表next,是算法的核心问题。这里我们引入一个概念f(j),其含义是,对于模式串的第j个字符pattern[j],f(j)是所有满足使pattern[1...k-1] = pattern[j-(k-1)...j - 1](k < j)成立的k的最大值。还是以模式串abcabcacab为例,当处理到pattern[8] = 'c'时,我们想找到'c'前面的k-1个字符,使得pattern[1...k-1] = pattern[8-(k-1)...7],这里我们可以使用一个笨法,让k-1从1到6递增,然后依次比较,直到找到最大值的k为止,比较过程如下
| k-1 | 前缀 | 关系 | 子串 |
| 1 | a | == | a |
| 2 | ab | != | ca |
| 3 | abc | != | bca |
| 4 | abca | == | abca |
| 5 | abcab | != | cabca |
| 6 | abcabc | != | bcabca |
| j | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| pattern[j] | a | b | c | a | b | c | a | c | a | b |
| next[j] | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 5 | 0 | 1 |
| f(j) | 0 | 1 | 1 | 1 | 2 | 3 | 4 | 5 | 1 | 2 |
如果 pattern[j] != pattern[f(j)],next[j] = f(j);
如果 pattern[j] = pattern[f(j)],next[j] = next[f(j)];
当要求f(9)时,f(8)和next[8]已经可以得到,此时我们可以考察pattern[next[8]],根据前面对于next值的计算方式,我们知道pattern[8] != pattern[next[8]]。我们的目的是要找到pattern[9]的包含前缀,而pattern[8] != pattern[5],pattern[1...5]!=pattern[4...8]。我们继续考察pattern[next[5]]。如果pattern[8]
= pattern[next[5]],假设next[5] = 3,说明pattern[1...2] = pattern[6...7],且pattern[3] = pattern[8],此时对于pattern[9]而言,就有pattern[1...3]=pattern[6...8],我们就找到了f(9) = 4。这里我们考察的是pattern[next[j]],而不是pattern[f(j)],这是因为对于next[]而言,pattern[j] != pattern[next[j]],而对于f()而言,pattern[j]与pattern[f(j)]不一定不相等,而我们的目的就是要在pattern[j]
!= pattern[f(j)]的情况下,解决f(j+1)的问题,所以使用next[j]向前回溯,是正确的。
现在,我们来总结一下next[j]和f(j)的关系,next[j]是所有满足pattern[1...k - 1] = pattern[(j - (k - 1))...j -1](k < j),且pattern[k] != pattern[j]的k中,k的最大值。而f(j)是满足pattern[1...k - 1] = pattern[(j - (k - 1))...j -1](k < j)的k中,k的最大值。还是以上例的模式来说,对于第7个元素,其f(j) = 4, 说明pattern[7]的前3个字符与模式的前缀3相同,但是由于pattern[7] = pattern[4], 所以next[7] != 4。
通过以上这些,读者可能会有疑问,为什么不用f(j)直接作为KMP算法的跳转表呢?实际从程序正确性的角度讲是可以的,但是使用next[j]作为跳转表更加高效。还是以上面的模式为例,当target[n]与pattern[7]发生匹配失败时,根据f(j),target[n]要继续与pattern[4]进行比较。但是在计算f(8)的时候,我们会得出pattern[7]
= pattern[4],所以target[n]与pattern[4]的比较也必然失败,所以target[n]与pattern[4]的比较是多余的,我们需要target[n]与更小的pattern进行比较。当然使用f(j)作为跳转表也能获得不错的性能,但是KMP三人将问题做到了极致。
我们可以利用f(j)作为媒介,来递推模式的跳转表next。算法如下:
- inline void BuildNext(const char* pattern, size_t length, unsigned int* next)
- {
- unsigned int i, t;
- i = 1;
- t = 0;
- next[1] = 0;
- while(i < length + 1)
- {
- while(t > 0 && pattern[i - 1] != pattern[t - 1])
- {
- t = next[t];
- }
- ++t;
- ++i;
- if(pattern[i - 1] == pattern[t - 1])
- {
- next[i] = next[t];
- }
- else
- {
- next[i] = t;
- }
- }
- //pattern末尾的结束符控制,用于寻找目标字符串中的所有匹配结果用
- while(t > 0 && pattern[i - 1] != pattern[t - 1])
- {
- t = next[t];
- }
- ++t;
- ++i;
- next[i] = t;
- }
程序中,9到27行的循环需要特别说明一下,我们发现在循环开始之后,就没有再为t赋新值,也就是说,对于计算next[j]时的t值,在计算next[j+1]时,还会用得着。实际这时的t的就等于f(j)。还是以上例的目标串为例,当j等于1,我们可以得出t = f(2) = 1。使用归纳法,当计算完next[j]后,我们假设此时t=f(j),此时第11~14行的循环就是要找到满足pattern[k] = pattern[j]的最大k值。如果这样的k存在,对于pattern[j+1]而言,其前k个元素,与模式的前缀k相同。此时的t+1就是f(j+1)。这时我们就要判断pattern[j+1]和pattern[t](t = t+1)的关系,然后求出next[j+1]。这里需要初始条件next[1] = 0。
利用跳转表实现字符串匹配的算法如下:
- unsigned int KMP(const char* text, size_t text_length, const char* pattern, size_t pattern_length, unsigned int* matches)
- {
- unsigned int i, j, n;
- unsigned int next[pattern_length + 2];
- BuildNext(pattern, pattern_length, next);
- i = 0;
- j = 1;
- n = 0;
- while(pattern_length + 1 - j <= text_length - i)
- {
- if(text[i] == pattern[j - 1])
- {
- ++i;
- ++j;
- //发现匹配结果,将匹配子串的位置,加入结果
- if(j == pattern_length + 1)
- {
- matches[n++] = i - pattern_length;
- j = next[j];
- }
- }
- else
- {
- j = next[j];
- if(j == 0)
- {
- ++i;
- ++j;
- }
- }
- }
- //返回发现的匹配数
- return n;
- }
该算法在原有基础上进行了扩展,在原模式串末尾加入了一个“空字符”,“空字符”不等于任何的可输入字符,当目标串匹配至“空字符”时,说明已经在目标字符串中发现了模式,将模式串在目标串中的位置,加入matchs[]数组中,同时判定为匹配失败,并根据“空字符”的next值,跳转到适当位置,这样算法就可以识别出字符串中所有的匹配子串。
最后,对KMP算法的正确性做一简要说明,还是以上文的模式串pattern和目标串target为例,假设已经匹配到第3部的位置,且在target[13]处发现匹配失败,我们如何决定模式串的滑动步数,来保证既要忽略不必要的多余比较,又不漏过可能的匹配呢?
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | |
| target | b | a | b | c | b | a | b | c | a | b | c | a | a | b | c | a | b | c | a | b | c | a | c | a | b | c |
| pattern | a | b | c | a | b | c | a | c | a | b |
对于例子中的情况,显然向后移动多于3个字符有可能会漏过target[9...18]这样的的可能匹配。但是为什么向后移动1个或者2个字符是不必要的多余比较呢?当target[13]与pattern[8]匹配失败时,同时也意味着,target[6...12]
= pattern[1...7],而next[8]=5,意味着,pattern[1...4] = pattern[4...7],pattern[1...5]
!= pattern[3...7],pattern[1...6]
!= pattern[2...7]。如果我们将模式串后移1个字符,使pattern[7]与target[13]对齐,此时target[7...12]相当于pattern[2...7],且target[7...12]与pattern[1..6]逐个对应,而我们已经知道pattern[1...6]
!= pattern[2...7]。所以不管target[13]是否等于pattern[7],此次比较都必然失败。同理向前移动2个字符也是多余的比较。由此我们知道当在pattern[j]处发生匹配失败时,将当前输入字符与pattern[j]和pattern[next[j]]之间的任何一个字符对齐执行的匹配尝试都是必然失败的。这就说明,在模式串从目标串头移动到目标串末尾的过程中,除了跳过了必然失败的情况之外,没有漏掉任何一个可能匹配,所以KMP算法的正确性是有保证的。
后记:
- 首先要感谢Knuth-Morris-Pratt那篇光辉的论文《Fast Pattern Matching In Strings》,让我们在字符串处理的道路上看得更远。本文的例子和思路,均完全来自这篇论文,论文后面还对KMP算法的时间复杂度进行了彻底的分析。
- KMP算法是一个高度优化的精妙算法,所以初涉该算法的时候,不要指望一蹴而就,一下子就将KMP算法理解透,而是应该循序渐进,逐步加深理解。据说该算法是Knuth,Morris,Pratt三人分别独立发现的,我斗胆揣测一下该算法的演进历程。首先应该是发现了模式串前缀的自包含问题,然后是提出了f(j)的概念,然后是搞定了如何计算f(j),然后提出了next[j]的概念,然后搞定了如何用f(j)计算next[j+1],然后是只用f(j)做中间结果直接算出next[j+1]。之所以我会这么猜测,主要是因为next跳转表的概念和生成算法太高端,中间经历了多个转换,极难一步到位想出来这么搞。所以我们也应该按照这个流程来学习KMP算法,而如何计算f(j)则是整个算法的精髓所在。
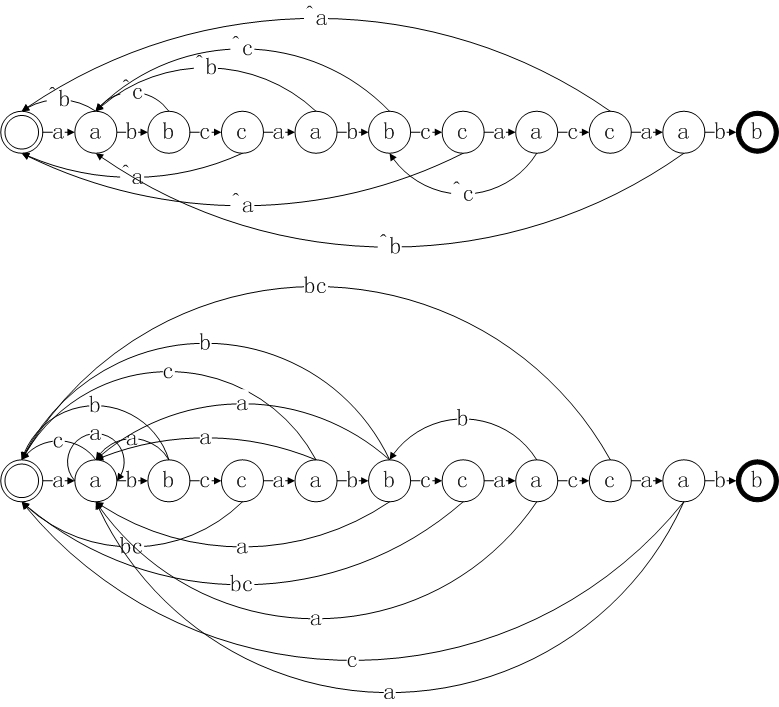
- 实际上,KMP算法中所用到的跳转表next是一个简化了的DFA,对于DFA而言,其跳转和输入的字符集有关,而KMP算法中的跳转表,对于模式串中的当前位置j-1,只有两种跳转方式pattern[j],和^pattern[j],所以KMP算法的跳转功能要弱于DFA,但是其构建速度,又大大快于DFA,在花费较小代价的同时,取得了逼近DFA的效果。下面是对于文中使用的模式串生成跳转表(上)和DFA的比较,显然DFA要复杂的多(这个是我手画的如果有画错的地方,请读者不吝赐教)。
之前我的《BM算法详解》一文中有一个巨大的缺憾,就是没能给出计算模式串好后缀跳转表的高效算法。Robert S.Boyer和J Strother Moore两人的论文中,不知什么原因,并没有给出这样的算法,蛮力算法O(n^3)的时间复杂度使得BM算法的实用性大打折扣。实际上线性时间内计算出模式串的好后缀跳转表的算法是存在,但是在介绍这个算法之前,我要向大家推荐一本字符串处理方面的权威著作《Algorithms on Strings,Trees and Sequences》,作者Dan Gusfield。书中几乎涵盖了当今具有实用价值的所有字符串处理技术,当然BM和KMP算法也涵盖其中,本文的内容就源于此书。不过这本书的内容可以说是非常非常的难,要想全部吃透十分不易。
在我的有关KMP,BM算法的两篇文章中,我已经提到了一个关键的问题,那就是前/后缀的自包含问题。无论是KMP算法还是BM算法的跳转表,都与自包含前/后缀有着直接的联系。这里我们需要引入一个概念Zi(S),其中S代表模式串,对于模式串S[1...n],Zi(S)表示子串S[i...j]的长度,其中j是所有满足S[i...j]=S[1...j-i+1]的j中的最大者。说起来挺玄乎,实际就是以i为起始的最长包含前缀。对于S=aabcaabxaaz,我们有
- Z5(S)=3,(aab)c(aab)xaaz
- Z6(S)=1,(a)abca(a)baaz
- Z7(S)=Z8(S)=0,当S[i]!=S[1]时Zi(S)=0
- Z9(S)=2,(aa)bcaabx(aa)z
由上面Z5(S)=3我们知道S[5...7]=S[1...3],且S[5...8]!=S[1...4],这里我们把S[5...7]叫做字符串S的一个Z-block,对于Zi(S),如果Zi(S)!=0,那么所标记的Z-block起始于i,结束于i+Zi(S)-1。显然,一个字符串可能包含若干个Z-block,而且各Z-block之间可能互相交叠。我们再定义两个值li,ri,其中li,ri是包含S[i]的所有Z-block中右端点最大的一个,如下图所示,这里包含i的Z-block有两个,只有标注a的Z-block的l值和r值,才是li和ri的实际值。实际上S[li...ri]=S[1...ri-li+1]。

现在我们就来介绍一下,在Z1(S),……,Zi(S),li,ri已知的情况下,如何求解Zi+1(S),这里我们令li=l, ri=r, i+1=k, i-li+2=k'。
1. 如果k,Zk'(S)与l,r的所决定的Z-block关系如下图所示,因为S[l...r]=S[1...r-l+1],所以我们可以把S[l...r]区间内的问题,放到S[1...r-l+1]区间内来考虑,此时k在1,r-l+1区间内的对应点就是k'。我们需要关注Zk'(S)这个已知量,在下图所示的这种情况中,Zk'(S)所决定Z-block完全包含在1,r-l+1区间内。也就是k'+Zk'(S)-1<r-l+1,此时Zk(S)实际上就等于Zk'(S)。

2. 如果k,Zk'(S)与l,r的所决定的Z-block关系如下图所示。此时,我们也同样将S[l...r]区间内的问题,放到S[1...r-l+1]区间内来分析。此时Zk'(S)所决定的Z-block的右端要超过r-l+1,也就是说对于Zk(S),我们已经知道其前r-k+1个元素与S[1...r-k+1]相同,但是对于S[r]以后的元素是否还可以与前面的r-k+1个元素连起来形成更长的包含前缀我们还只有进行比较后才能知道。由于之前我们的已经有S[k...r]=S[k'...r-l+1]=S[1...r-k+1](注意图中几个标注beta的区域),所以我们可以省去对这两个区间的比较,直接从S[r-k+2]开始与S[r-k+2]进行比较,直到匹配失败为止,此时我们就得到新的右端点ri+1,同时将li+1更新为i+1。

3. 如果r<=k。那么之前计算出的Z-block对我们没有任何帮助,我们从r开始,找到最小的k,使得S[r...k]!=S[1...r-k+1]。此时我们同时还要更新对应的li+1=i+1,ri+1=k-1。
分别处理上述三种情况,我们就可以在线性时间内,递推填写S[1...n]的所有Zi(S)值。假设模式串S="aabaabcaxaabaabcy",其对应的Zi(S)值如下表。
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | |
| S | a | a | b | a | a | b | c | a | x | a | a | b | a | a | b | c | y |
| Zi(S) | 0 | 1 | 0 | 3 | 1 | 0 | 0 | 1 | 0 | 6 | 1 | 0 | 3 | 1 | 0 | 0 | 0 |
当我们要计算Z12(S)时,Z1(S)到Z11(S)都已经计算得到,此时的l=10,r=15,也就是说S[10...15]所形成的Z-block是当前的最右Z-block且包含S[12]。此时我们要计算Z12(S),由于S[10...15]=S[1...6],所以Z12(S)与Z3(S)密切相关,我们发现Z3(S)=0,3+Z3(S)=3<6,这个符合前面的第一种情况,所以Z12(S)=Z3(S)=0.
对于Z10(S),当计算Z10(S)时,已知的最右Z-block是S[8],l=8,r=8,因为10>8,所以符合上述第三种情况,我们直接从S[10]开始向后寻找S的包含前缀,找到S[10...15]是一个长度为6的S的包含前缀,所以Z10(S)=6,同时更新l=10,r=15.
在Zi(S)值计算中,第二种情况的场景比较少见,但是第二种情况也是Zi(S)计算中最容易出问题的部分。
下面给出我自己写的计算Z数组的算法
- void ZBlock(const char* pattern, unsigned int length, unsigned int zvalues[])
- {
- unsigned int i, j, k;
- unsigned int l, r;
- l = r = 0;
- zvalues[0] = 0;
- for(i = 1; i < length; ++i)
- {
- if(i >= r)
- {
- j = 0;
- k = i;
- zvalues[i] = 0;
- while(k < length && pattern[j] == pattern[k])
- {
- ++j;
- ++k;
- }
- if(k != i)
- {
- l = i;
- r = k - 1;
- zvalues[i] = k - i;
- }
- }
- else
- {
- if(zvalues[i - l] >= r - i + 1)
- {
- j = r - i + 1;
- k = r + 1;
- while(k < length && pattern[j] == pattern[k])
- {
- ++j;
- ++k;
- }
- l = i;
- r = k - 1;
- zvalues[i] = k - i;
- }
- else
- {
- zvalues[i] = zvalues[i - l];
- }
- }
- }
- }
因为普通的字符串是从索引0开始,所以算法中对此作了调整。
Z-block算法从理论上彻底解决了前缀自包含的计算问题,从易理解的角度上讲,Z-block算法也要明显优于KMP算法中三人对next表构造过程的描述。拥有了模式串的Z值数组后,相应的KMP算法的next跳转表,BM算法的好后缀表的计算都将变得高效,直观。
KMP算法中next[i]与Zi(S)的对应关系
我在《KMP算法详解》一文中已经介绍了next[i]的含义,对于S[i],next[i]的意义是,如果存在k使得S[1...i-k]=S[k...i-1]且S[i-k+1]!=S[i],那么next[i]=i-k+1。实际上对于满足条件的k,其Z值Zk(S)就满足k+Zk(S)=i,next[i]=Zk(S)+1,所以我们可以用如下方法根据模式串S的Zi(S)表填写对应的next[i]表。
规则一,从头到尾遍历Zi(S),当遍历到元素k时,如果Zk(S)!=0,那么next[k+Zk(S)]=Zk(S)+1,如果还存在k'使得k+Zk(S)=k'+Zk'(S)那么next[k+Zk(S)]等于Zk(S)+1与Zk'(S)+1的较大者。
规则二,对于遍历Zi(S)列表之后,尚未填写的元素的next值,我们按照如下原则填充,对于元素S[i],如果S[i]=S[1],则其next值next[i]=0,否则next[i]=1。
根据上面的原则,我们对于《KMP算法详解》中的老例子通过Zi(S)构建next[i]的表格如下。这里对于S[8],由于4+Z4(S)=8,7+Z7(S)=8,所以我们选择其中的较大者Z4(S)=4,令next[8]=Z4(S)+1=5。对于S[9],由于9+Z9(S)超出了pattern数组的范围,所以我们不使用该Z值计算next跳转表。实际对于下表,除了next[8]之外,其余均是由规则二填写。相较于KMP三人给出的next表填写算法,利用Z值表填写next表固然增加了一个转换层,降低了算法效率,但是从易理解的角度讲,由Z值到next值的转换是十分有意义的。
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| pattern | a | b | c | a | b | c | a | c | a | b |
| Zi(S) | 0 | 0 | 0 | 4 | 0 | 0 | 1 | 0 | 2 | 0 |
| next | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 5 | 0 | 1 |
BM算法goodsuffix[i]与Zi(S)的对应关系
用Z值表填写goodsuffix表的过程,要比填写next表复杂得多。首先,BM算法使用的是后缀自包含而Z值计算的是前缀,另一方面我们还需要找到最长的与后缀相匹配的前缀的长度,来修正跳转值。这里我们分别来处理这两个问题。
对于BM算法中的模式串S,我们可以计算其逆串Sr的Z值,Zi(Sr)。例如,对于S="abcxxxabc",Sr="cbaxxxcba",我们可以得到Sr的Z值表如下图所示
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| Sr | c | b | a | x | x | x | c | b | a |
| Zi(Sr) | 0 | 0 | 0 | 0 | 0 | 0 | 3 | 0 | 0 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| S | a | b | c | x | x | x | a | b | c |
| rpr(i) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
之后,我们可以计算出未修正的好后缀跳转表。对于rpr(i)=0的元素,goodsuffix'[i]=patlen+n-i,对于rpr(i)!=0的元素,goodsuffix'[i]=n-rpr(i),其中n是模式串最末元素的索引值。如果模式串的首字符从0开始的话,n!=patlen这里要特别注意。
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| S | a | b | c | x | x | x | a | b | c |
| goodsuffix' | 17 | 16 | 15 | 14 | 13 | 12 | 11 | 10 | 1 |
另外,我们还需要找到与后缀匹配的最长前缀p,用于修正goodsuffix'的跳转步数。p值在构建Zi(Sr)的时候可以得到,对于Sr中的元素Sr[i],如果有i+Zi(Sr)-1=n,那么p=Zi(Sr),如果有多个i满足该条件,则p等于其中的最大者。上例中对于Sr="cbaxxxcba",我们有7+Z7(Sr)-1=9,所以p=Z7(Sr)=3。在修正goodsuffix'的跳转步数时,我们对于n-i>=p的元素goodsuffix'值统一减去p即可得到最终的goodsuffix值。如下图
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| S | a | b | c | x | x | x | a | b | c |
| goodsuffix | 14 | 13 | 12 | 11 | 10 | 9 | 11 | 10 | 1 |
上面虽然列出了4个步骤,但是在实际计算BM的好后缀跳转表的过程中,除了Zi(Sr)需要单独计算之外,其余三个步骤,可以一次完成。
在使用Z值表计算KMP算法或者是BM算法的跳转表的过程中,模式串起始索引要特别注意,如果S[0...n]从0开始,则要对一些地方做修正。因为如果模式串从索引0的位置开始,其最末元素n!=patlen,所以在计算过程中,哪里用的是模式串的长度,哪里用的是模式串最末元素的索引,要格外留心。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号