题解 [APIO2014]连珠线

题解 [APIO2014]连珠线

题面

解析

首先这连成的是一棵树啊.

并且\(yy\)一下,如果钦定一个根,

那么这上面的蓝线都是爸爸->儿子->孙子这样的,因为像下图这样的构造不出来:

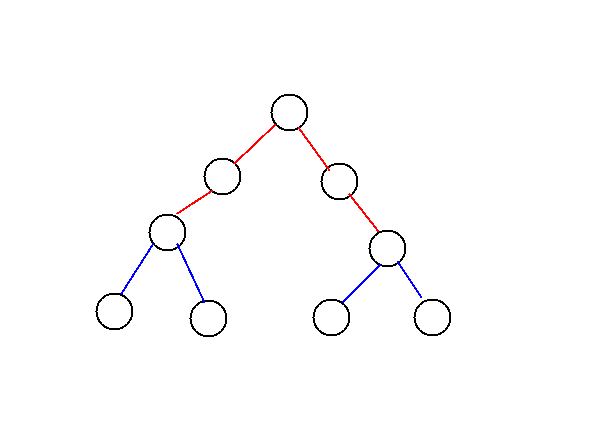
(兄弟到兄弟的特殊情况不用考虑,因为会在一个端点作为根的情况考虑的)

那么首先还是来简单的写法,

设\(f[i][0/1]\)表示\(i\)是否为一根蓝线的中点的最大分数,

也可以理解为从\(i\)的一个儿子到\(i\)在上去还有没有蓝线.

并且,\(f[i][1]\)要算上它到父亲的边权.

然后再设\(c[i]\)=\(\max(f[i][0],f[i][1])\),

主要是懒得写

那么\(f[i][0]=\sum_{k=son[i]}c[k]\),

而\(f[i][1]=f[i][0]+\max(f[k][0]+w[k]-c[k])\),

其中\(w[k]\)表示\(k\)到父亲的边权(也就是i到k)

跑\(n\)遍dfs即可.

但这显然可以换根DP啊.

设\(dp[i]\)表示以\(i\)为根的最大分数,

\(v[i]\)表示\(i\)的父亲作为一条蓝边的中点,而\(i\)是一个端点的分数,并且也要再算上\(fa\)到\(i\)这条边.

(可以理解为f[fa][1]伸出去的那条边到了\(i\)这里)

那么有\(dp[i]=f[i][0]+max(dp[fa]-c[i],v[i])\)

就是\(i\)子树里的贡献加上父亲的贡献.

而父亲的贡献要么是不连边(\(dp[fa]-c[i]\)),要么就连边(v[i]).

(把\(f[i][0]\)式子里的\(c[k]\)换成\(c\)的定义就会发现很像)

然后考虑怎么求\(v\).

这里我们是用父亲去求儿子,

也就是当前是\(i\)时,我们考虑求\(i\)的儿子\(k\)(们)的\(v[k]\).

首先\(k\)是一个端点,那么我们要在\(i\)的儿子里再找出一个端点,

这里我们记一个\(mx1\)代表更新\(f[x][1]\)时后面那一串max(f[k][0]+w[k]-c[k])的最大值,

\(mx2\)表示次大值,\(id\)表示值为\(mx1\)的\(k\).

然后在求\(v[k]\)时,我们就有:

• \(v[k]=dp[i]-c[k]+mx1+w[i]\),\(k\not=id\)

  这时我们可以直接拿最大值来贡献到\(k\)

• \(v[k]=dp[i]-c[k]+mx2+w[i]\),\(k=id\)

  因为\(k\)已经是最大值的端点了,所以只能拿次大值来更新.

注意,\(mx1\)和\(mx2\)都要算上父亲!!!

显然父亲也会有贡献.

而父亲的贡献是dp[fa]-c[x]+w[i]-max(dp[fa]-c[x],v[x])

其实和上面的式子的结构是一样的(\(dp[fa]-c[x]\)就是\(f[k][0]\),\(\max(dp[fa]-c[x],v[x])\)就是\(c\))

然后就没有然后了

code:

#include <iostream>
#include <cstdio>
#include <cstring>
#define int long long
using namespace std;

inline int read(){
	int sum=0,f=1;char c=getchar();
	while(c>'9'||c<'0'){if(c=='-') f=-1;c=getchar();}
	while(c<='9'&&c>='0'){sum=(sum<<3)+(sum<<1)+c-'0';c=getchar();}
	return sum*f;
}

const int N=200005;
const int INF=1e18;
struct edge{int to,next,w;}e[N<<1];
struct node{int mx1,mx2,id;}a[N];
int n;
int f[N][2],c[N],v[N],dp[N];
int head[N],cnt=0;

inline void add(int x,int y,int w){
	e[++cnt]=(edge){head[x],y,w};head[x]=cnt;
}

inline void dfs(int x,int fa){
	int ok=0;
	for(int i=head[x];i;i=e[i].to){
		int k=e[i].next;
		if(k==fa) continue;
		f[k][1]+=e[i].w;
		dfs(k,x);ok=1;
		f[x][0]+=c[k];
		if(f[k][0]+e[i].w-c[k]>a[x].mx1)
			a[x].mx2=a[x].mx1,a[x].mx1=f[k][0]+e[i].w-c[k],a[x].id=k;
		else if(f[k][0]+e[i].w-c[k]>a[x].mx2)
			a[x].mx2=f[k][0]+e[i].w-c[k];
	}
	f[x][1]+=f[x][0]+a[x].mx1;
	if(!ok) f[x][1]=-INF;
	c[x]=max(f[x][0],f[x][1]);
}

inline void dfs1(int x,int fa){	
	dp[x]=f[x][0]+max(dp[fa]-c[x],v[x]);
	for(int i=head[x];i;i=e[i].to){
		int k=e[i].next;
		if(k==fa) continue;
		if(k==a[x].id) v[k]=dp[x]-c[k]+a[x].mx2+e[i].w;
		else v[k]=dp[x]-c[k]+a[x].mx1+e[i].w;
		int ret=dp[x]-c[k]+e[i].w-max(dp[x]-c[k],v[k]);
		if(ret>a[k].mx1) a[k].mx2=a[k].mx1,a[k].mx1=ret,a[k].id=x;
		else if(ret>a[k].mx2) a[k].mx2=ret;
		dfs1(k,x);
	}
}

signed main(){
	n=read();
	for(int i=1;i<n;i++){
		int x=read(),y=read(),w=read();
		add(x,y,w);add(y,x,w);
	}
	for(int i=1;i<=n;i++) a[i].mx1=a[i].mx2=-INF;
	dfs(1,0);dfs1(1,0);
	int ans=0;
	for(int i=1;i<=n;i++) ans=max(ans,dp[i]);
	printf("%lld\n",ans);
	return 0;
}