网络流

网络流

不说废话。

概念

网络，对于一张有向连通图 \(G=(V,E)\)，其中分别有且仅有一个 \(s \in V,t \in V\)，且 \(s\) 无入度，\(t\) 无出度，则我们称 \(G\) 是一个网络。其中我们称 \(s\) 为源点，\(t\) 为汇点。

对于一个网络，其需要满足一下性质：

• 对于一条边 \((u,v) \in E\)，定义 \(c(u,v)\) 为其流量，\(f(u,v)\) 为其容量，且要求 \(c(u,v) \le f(u,v)\)。

• 对于一个点 \(u \in V\)，称其净流量为其总流入减总流出，且除了 \(s\) 和 \(t\) 外，要求其流入等于其流出，即对于任意 \(u \ne {s,t}\)，\(u\) 的净流量为 \(0\)。

定义一个边 \((u,v)\) 的剩余容量为其 \(f(u,v)-c(u,v)\) 即容量减流量，记作 \(c_f(u,v)\)。定义剩余流量不为 \(0\) 的边和节点构成的子图为残量网络。记作 \(G_f\)。

不难发现，\(s\) 的流出等于 \(t\) 的流入。我们称整个网络的流为 \(s\) 的流出即 \(t\) 的流入。

我们把 \(G_f\) 中一条 \(u\) 到 \(v\)​ 的路径称作增广路。

我们对于一条增广路，给每一条边都加上一个相等的流量，我们称这个过程为增广。

另外，反向边为一条 \(G\) 中一条边的反向边即 \((v,u)\)，且 \(f(v,u) = -f(u,v)\)。

最大流

对于一个网络，找到一个流，使得流的流量最大。

板子题：

P3376 【模板】网络最大流

给定一个网络以及其源点、汇点，求其网络最大流。

\(1 \le n \le 200\), \(1 \le m \le 5000\)，\(0 \le w \le 2^{31}\)。

FF 算法

FF 算法即 Ford-Fulkerson 算法。

首先考虑最暴力的策略。每次只要找到一条增广路，便对他进行增广。重复此流程，直到网络中不存在增广路。

显然，这个是假的贪心。随意找一个例子就可以卡掉。

我们拿下面的这幅图举例子（如图 1，图中边权标注的是剩余容量）。首先我们找到一条增广路 \(1 \rightarrow 2 \rightarrow 3 \rightarrow 4\) 并且对他进行增广，这些边剩余容量变为 \(0\)。然后图中不存在其余增广路（如图 2），最终求得此网络的流为 \(1\)。

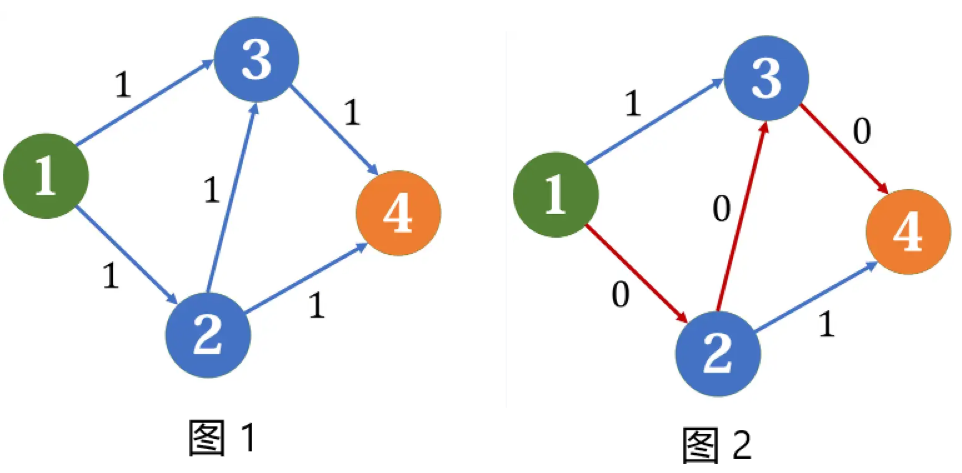
然而，不难发现，如果我们对于 \(1 \rightarrow 3 \rightarrow 4\) 和 \(1 \rightarrow 2 \rightarrow 4\) 分别进行增广，得到的流量为 \(2\)。

为了解决这样的问题，我们引入反向边，反向边为一条 \(G\) 中一条边的反向边即 \((v,u)\)，且我们约定 \(c(v,u) = -c(u,v)\)。为了满足这样的性质，在对 \((u,v)\) 的流量加 \(val\) 时，需要给其反向边的流量减 \(val\)。

以此，我们可以借助反向边解决问题。（如图 3）

我们不妨将反向边当作正常的边进行处理。

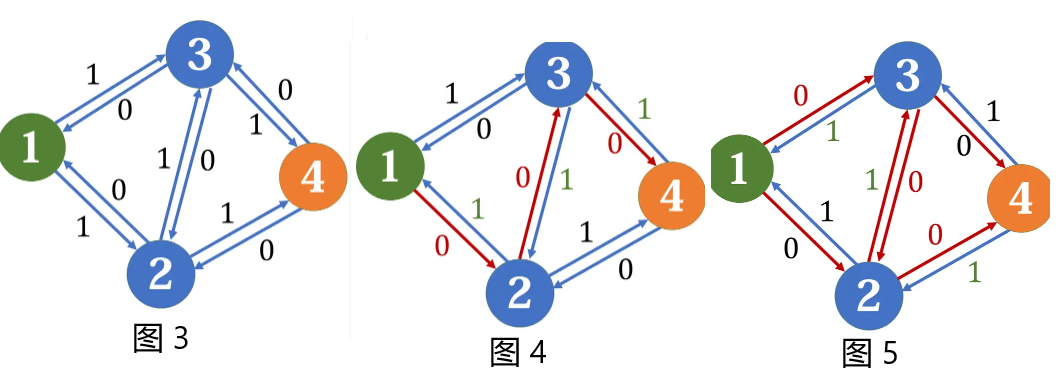
我们还是正常找一条增广路进行增广，然后这条增广路上的边的流量增加，同时其反向边的流量相应的减少，其剩余流量自然跟随变化（如图 4）。但是此时，我们在进行以此增广之后，你就发现你还可以找到一条增广路 \(1 \rightarrow 3 \rightarrow 2 \rightarrow 4\)，对他进行增广。进行完这些操作后，得到最大流量 \(2\)（如图 5）。

仔细观察不难发现，第二次增广时，当 \((2,3)\) 的反向边被增广后，\((2,3)\) 相当于没有被增广过。所以，反向边相当于一个“撤销”操作。

这就是 FF 算法的核心思想。可以使用 DFS 实现。但是时间复杂度过高。下面考虑优化。

EK 算法

EK 算法即 Edmonds-Karp 算法。核心思想在于利用 bfs 进行 FF 增广。

大致流程如下：

1. 在 \(G_f\) 上找一条增广路。
2. 在增广路上求出剩余容量的最小值，然后给增广路上边的流量加上他，给对应的反向边的容量减去他。
3. 重复 1、2，直到没有增广路。

依此，便可以求出该网络的最大流量。单轮增广的时间复杂度为 \(O(E)\)，增广轮数理论上界为 \(O(VE)\)，那么 EK 算法总的时间复杂度为 \(O(VE^2)\)。

Dinic 算法

Dinic 算法是求解最大流问题的主流算法。是对于 FF/EK 的优化。

对于每一次增广，首先 bfs 对图按照 \(dis(s,u)\) 进行分层。我们让每个点 \(u\) 只能向自己的下一层的点 \(v\) 进行增广。这样每次增广的都是原图中边数最少的路径，且可以保证不会因为反向边的缘故让接下来的 dfs 陷入死循环。

分层之后，从 \(s\) 开始 dfs。区别于 EK，我们对于一个点 \(u\)，如果他从他的一个儿子找到了增广路，不必回到 \(s\) 进行再次处理，可以直接继续从 \(u\) 进行增广。

然后我们就可以写出复杂度较为正确的求最大流代码。

点击查看代码

#include <bits/stdc++.h>
#define il inline
#define int long long

using namespace std;

bool Beg;
namespace Zctf1088 {
namespace IO {
	const int bufsz = 1 << 20;
	char ibuf[bufsz], *p1 = ibuf, *p2 = ibuf;
	#define getchar() (p1 == p2 && (p2 = (p1 = ibuf) + fread(ibuf, 1, bufsz, stdin), p1 == p2) ? EOF : *p1++)
	il int read() {
		int x = 0; char ch = getchar(); bool t = 0;
		while (ch < '0' || ch > '9') {t ^= ch == '-'; ch = getchar();}
		while (ch >= '0' && ch <= '9') {x = (x << 1) + (x << 3) + (ch ^ 48); ch = getchar();}
		return t ? -x : x;
	}
	char obuf[bufsz], *p3 = obuf, stk[50];
	#define flush() (fwrite(obuf, 1, p3 - obuf, stdout), p3 = obuf)
	#define putchar(ch) (p3 == obuf + bufsz && flush(), *p3++ = (ch))
	il void write(int x, bool t = 0) {
		int top = 0;
		x < 0 ? putchar('-'), x = -x : 0;
		do {stk[++top] = x % 10 | 48; x /= 10;} while(x);
		while (top) putchar(stk[top--]);
		t ? putchar(' ') : putchar('\n');
	}
	struct FL {
		~FL() {flush();}
	} fl;
}
using IO::read; using IO::write;
const int N = 205, M = 1e4 + 10;
const int INF = 0x3f3f3f3f3f3f3f3f;
int n, m, S, T;
struct Edge {
	int nxt, to, w;
} edge[M];
int head[M], tot = 1;
il void addEdge(int x, int y, int w) {
	edge[++tot] = {head[x], y, w};
	head[x] = tot;
}
int dis[N];
queue<int> q;
il bool bfs() {
	for (int i = 1; i <= n; i++) dis[i] = 0;
	while (!q.empty()) q.pop();
	q.push(S);
	dis[S] = 1;
	while (!q.empty()) {
		int x = q.front(); q.pop();
		for (int i = head[x]; i; i = edge[i].nxt) {
			int y = edge[i].to, w = edge[i].w;
			if (w > 0 && dis[y] == 0) {
				dis[y] = dis[x] + 1;
				if (y == T) return true;
				q.push(y);
			}
		}
	}
	return false;
}
il int dfs(int x, int flow) {
	if (x == T) return flow;
	int rest = flow;
	for (int i = head[x]; i; i = edge[i].nxt) {
		int y = edge[i].to, w = edge[i].w;
		if (w > 0 && dis[y] == dis[x] + 1) {
			int k = dfs(y, min(rest, w));
			rest -= k;
			edge[i].w -= k;
			edge[i ^ 1].w += k;
		}
	}
	return flow - rest;
}
il int dinic() {
	int res = 0;
	while (bfs()) res += dfs(S, INF);
	return res;
}
signed main() {
	n = read(), m = read(), S = read(), T = read();
	for (int i = 1; i <= m; i++) {
		int x = read(), y = read(), w = read();
		addEdge(x, y, w);
		addEdge(y, x, 0);
	}
	write(dinic());
    
	return 0;
}}
bool End;
il void Usd() {cerr << "\nUse: " << (&Beg - &End) / 1024.0 / 1024.0 << "MB " << (double)clock() * 1000.0 / CLOCKS_PER_SEC << "ms\n";}
signed main() {
	Zctf1088::main();
	Usd();
	return 0;
}

但是这篇代码依然无法通过最大流板子题。

我们需要一个优化：当前弧优化。

考虑对于一个节点，从他的一个儿子走下去找到了增广路回来后，一定是一下两种情况之一：

1. 当前节点的流入还有剩余，说明从这个儿子走下去已经没有剩余容量了，从这个儿子走下去已经被填满了。那么以后就没有必要再走这个节点了。
2. 当前节点的流入没有剩余，说明从这个儿子走下去可能还有剩余，但是后面的儿子给到的流出一定是 \(0\)，因为当前节点已经没有剩余的流了。直接 break 掉即可。

无论是以上两种情况，我们都会发现，我们再次到这个节点时，肯定就不需要再走这个儿子之前的儿子了，因为他们肯定已经被处理完了。那么我们每次走到 \(u\) 的一个儿子 \(v\)，就令 \(cur_u=v\)，下一次就不从 \(head_u\) 开始遍历，而是 \(cur_u\)。

那么就考虑在实现 dinic 时加上面三条优化。

于是我们 dinic 的复杂度就可以得到保证。时间复杂度为 \(O(V^2E)\)。

点击查看代码

#include <bits/stdc++.h>
#define il inline
#define int long long

using namespace std;

bool Beg;
namespace Zctf1088 {
namespace IO {
	const int bufsz = 1 << 20;
	char ibuf[bufsz], *p1 = ibuf, *p2 = ibuf;
	#define getchar() (p1 == p2 && (p2 = (p1 = ibuf) + fread(ibuf, 1, bufsz, stdin), p1 == p2) ? EOF : *p1++)
	il int read() {
		int x = 0; char ch = getchar(); bool t = 0;
		while (ch < '0' || ch > '9') {t ^= ch == '-'; ch = getchar();}
		while (ch >= '0' && ch <= '9') {x = (x << 1) + (x << 3) + (ch ^ 48); ch = getchar();}
		return t ? -x : x;
	}
	char obuf[bufsz], *p3 = obuf, stk[50];
	#define flush() (fwrite(obuf, 1, p3 - obuf, stdout), p3 = obuf)
	#define putchar(ch) (p3 == obuf + bufsz && flush(), *p3++ = (ch))
	il void write(int x, bool t = 0) {
		int top = 0;
		x < 0 ? putchar('-'), x = -x : 0;
		do {stk[++top] = x % 10 | 48; x /= 10;} while(x);
		while (top) putchar(stk[top--]);
		t ? putchar(' ') : putchar('\n');
	}
	struct FL {
		~FL() {flush();}
	} fl;
}
using IO::read; using IO::write;
const int N = 205, M = 1e4 + 10;
const int INF = 0x3f3f3f3f3f3f3f3f;
int n, m, S, T;
struct Edge {
	int nxt, to, w;
} edge[M];
int head[M], tot = 1, cur[M];
il void addEdge(int x, int y, int w) {
	edge[++tot] = {head[x], y, w};
	head[x] = tot;
}
int dis[N];
queue<int> q;
il bool bfs() {	// 判断有无增广路并对图进行分层
	for (int i = 1; i <= n; i++) dis[i] = 0, cur[i] = head[i];
	while (!q.empty()) q.pop();
	q.push(S);
	dis[S] = 1;
	while (!q.empty()) {
		int x = q.front(); q.pop();
		for (int i = head[x]; i; i = edge[i].nxt) {
			int y = edge[i].to, w = edge[i].w;
			if (w > 0 && dis[y] == 0) {
				dis[y] = dis[x] + 1;
				if (y == T) return true;
				q.push(y);
			}
		}
	}
	return false;
}
il int dfs(int x, int flow) {	// 上一层传入的流量
	if (x == T) return flow;	// 找到汇点返回
	int rest = flow;	// 当前节点剩余的可分配流量
	for (int i = cur[x]; i; i = edge[i].nxt) {
		cur[x] = i;	// 当前弧优化
		int y = edge[i].to, w = edge[i].w;
		if (w > 0 && dis[y] == dis[x] + 1) {// 还有剩余流量在下一层
			int k = dfs(y, min(rest, w));	// 计算下面层能经过的流量
			if (k == 0) dis[y] = 0;
			rest -= k;
			edge[i].w -= k;		// 剩余流量减少
			edge[i ^ 1].w += k;	// 反向边剩余流量增加
		}
	}
	return flow - rest;
}
il int dinic() {
	int res = 0;
	while (bfs()) res += dfs(S, INF);	// 重复找增广路并 dfs 的过程直到没有增广路
	return res;
}
signed main() {
	n = read(), m = read(), S = read(), T = read();
	for (int i = 1; i <= m; i++) {
		int x = read(), y = read(), w = read();
		addEdge(x, y, w);
		addEdge(y, x, 0);	// 加反向边
	}
	write(dinic());
	
	return 0;
}}
bool End;
il void Usd() {cerr << "\nUse: " << (&Beg - &End) / 1024.0 / 1024.0 << "MB " << (double)clock() * 1000.0 / CLOCKS_PER_SEC << "ms\n";}
signed main() {
	Zctf1088::main();
	Usd();
	return 0;
}