2025年7月模拟赛整合

2025年7月模拟赛整合

2025CSP-S模拟赛11

T1 异或

10pts~50pts

简单的暴力。基础的暴力统计，或者拿数据结构简单维护。

80pts

这一档部分分是三角形直接到底。考虑乱搞吧。正解是三角形差分。考试时想到了一种奇奇怪怪的方法搞出了这一档，看代码吧。

for (int i = 1; i <= qq; i++) {
    int x = read(), y = read(), l = read(), v = read();
    int a = min(n + 1, x + l), b = min(n + 1, y + l);
    t[x][y] += v;
    t[a][b] -= v;
}
for (int j = 1; j <= n; j++) {
    for (int i = 1; i <= n; i++) {
        s[i][j] += t[i][j];
        s[i + 1][j] += s[i][j];
        t[i + 1][j + 1] += t[i][j];
    }
}
int ans = 0;
for (int i = 1; i <= n; i++) {
    for (int j = 1; j <= n; j++) {
        ans ^= s[i][j];
    }
}

100pts

正解和上一档很像了。

a
aa
aaa
bbbc
bbbcc
bbbccc
bbbcccc

这样就很直观了。把一个三角形转化成一个大三角形减去一个小三角形再减去一个矩形。其中，大小两个三角形都是到底的，直接和上一档一样的处理方式。至于矩形，考虑使用二维差分进行区间修改。

只不过考试时没有想出来这一档。

#include <bits/stdc++.h>
#define int long long

using namespace std;

int read() {
	int x = 0; char ch = getchar();
	while (ch < '0' || ch > '9') ch = getchar();
	while (ch >= '0' && ch <= '9') {
		x = (x << 1) + (x << 3) + (ch ^ 48);
		ch = getchar();
	}
	return x;
}
const int N = 1e3 + 10, M = 3e5 + 10;
int n, qq;
int t[N][N], s[N][N], f[N][N]; 
void add(int i, int j, int x, int y, int v) {
	f[i][j] += v;
	f[x + 1][j] -= v;
	f[i][y + 1] -= v;
	f[x + 1][y + 1] += v;
}
signed main() {
	n = read(), qq = read();
	for (int i = 1; i <= qq; i++) {
		int x = read(), y = read(), l = read(), v = read();
		int a = min(n + 1, x + l), b = min(n + 1, y + l);
		t[x][y] += v;
		t[a][b] -= v;
		add(a, y, n, b - 1, -v);
	}
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= n; j++) {
			f[i][j] = f[i - 1][j] + f[i][j - 1] - f[i - 1][j - 1] + f[i][j];
		}
	}
	for (int j = 1; j <= n; j++) {
		for (int i = 1; i <= n; i++) {
			s[i][j] += t[i][j];
			s[i + 1][j] += s[i][j];
			s[i][j] += f[i][j];
			t[i + 1][j + 1] += t[i][j];
		}
	}
	int ans = 0;
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= n; j++) {
			ans ^= s[i][j];
		}
	}
	printf("%lld\n", ans);
	
	return 0;
}

T2 游戏

博弈论。

考虑把这么多种情况的这棵二叉树画出来。很明晰了。

那我们对于解决这道题而言就考虑建出这棵二叉树，然后直接在二叉树上查询。具体做法类似于动态开点线段树。

建树。考虑将元素一个一个插入树中。我们在树中插入一个新值时，首先检查节点是否存在，若不存在则创建新节点。然后模拟题目按照取模是否为零让他分别进入左右子树即可。在叶子节点累加即可。

查询。首先，我们到一个节点时先检索当前节点是否存在，若不存在直接返回 0 即可。根据当前深度，如果是 Alice 在操作则返回左右儿子的较小值，否则 Bob 在操作返回较大值。

考虑保证时间复杂度。对于先手而言，如果每次都选择集合较小的一侧，那么每次操作集合大小至少减半，只需要 \(\log n\) 次操作就必定可以使答案为 0，考虑上“两人轮流操作”这个因素，所以当 \(m>2\times \log n\) 时，答案不可能大于 \(0\)。同理答案也不可能小于 \(0\)。因此当 \(m>2\times\log n\) 时答案一定为 \(0\)。故只在 \(m<\log n\) 时进行如上的二叉树操作，保证时间复杂度为 \(O(n\log n)\)。

#include <bits/stdc++.h>
#define int long long

using namespace std;

int read() {
	int x = 0, f = 1; char ch = getchar();
	while (ch < '0' || ch > '9') {
		if (ch == '-') f = -1;
		ch = getchar();
	}
	while (ch >= '0' && ch <= '9') {
		x = (x << 1) + (x << 3) + (ch ^ 48);
		ch = getchar();
	}
	return x * f;
}
const int N = 2e5 + 10;
int n, m, a[N], b[N];
struct Tree {
	int s[N * 30], lc[N * 30], rc[N * 30];
	int tot;
	void insert(int &p, int dep, int v) {
		if (!p) p = ++tot;
		if (dep > m) {
			s[p] += v;
			return;
		}
		if (v % b[dep] != 0) insert(lc[p], dep + 1, v);
		else insert(rc[p], dep + 1, v);
	}
	int query(int p, int dep) {
		if (!p) return 0;
		if (dep > m) return s[p];
		int res1 = query(lc[p], dep + 1);
		int res2 = query(rc[p], dep + 1);
		if (dep % 2 == 1) return min(res1, res2);
		else return max(res1, res2);
	}
} tr; 
signed main() {
	n = read(), m = read();
	if (m > 2 * log2(n)) { // max=28
		printf("0\n");
		return 0;
	}
	for (int i = 1; i <= n; i++) a[i] = read();
	for (int i = 1; i <= m; i++) b[i] = read();
	int root = 0;
	for (int i = 1; i <= n; i++) {
		tr.insert(root, 1, a[i]);
	}
	printf("%lld\n", tr.query(root, 1));
	
	return 0;
}

T3 连通块

这道题一步一步来。

基本思路

对于小规模的数据直接上暴力代码。

  1. \(O(n^2)\) 建图。
  2. 枚举删除的节点。
  3. dfs 统计最大连通块大小。

初步优化

这边有一些剪枝。

  1. 我们关注到删除一个点后最大连通块，要么是将原图中最大连通块断成两个中的一个，要么是原图中第二大的连通块。因此，断点断在原图最大连通块上一定是最优的。那么我们可以考虑用并查集找出原图最大连通块以及第二大连通块大小。
  2. 关注到要使最大连通块能被断成两个，那么断掉的这个点一定是原图上的割点。考虑用 tarjan 处理处原图上的割点并只对割点进行处理。

没写完，先咕着。

T4 公交路线

2025CSP-S模拟赛12

诈骗场。事实上，这场原来的题目顺序是现在的T4T3T2T1。

T1 环游(tour)

这题随便乱搞写个假做法有 80pts。。

直接来看满分做法。

关注到 \(V\) 最多只会变化 \(\lfloor\log V\rfloor\) 次。而且对于一层而言，走的范围都形成一个连续段。那问题就转化为了：能否使每一层的连续段覆盖所有点。

考虑状压 dp，设 \(f_s\) 表示当前选了 \(s\) 这些层，可以覆盖的最长前缀。类似的，我们定义 \(g_s\) 表示可以覆盖的最长后缀。转移的话比较简单，枚举然后刷表转移就行了。考虑到起点是包含在第一层的区间内的，所以此处的转移不包含第一层，也就是状态要比总层数少一。

这边我们发现时间在处理可以覆盖到哪里的时候复杂度略高，可以考虑预处理每一层从某个点开始能向左/向右走到哪里。

考虑统计答案。那无非就是第一层的范围再加上一个前缀一个后缀。考虑枚举前缀的状态，后缀的状态就是补集。然后就是 \((f_s\geq l-1)\cup(g_{\bar{s}}\le r+1)\)。不难理解。

#include <bits/stdc++.h>

using namespace std;

int read() {
	int x = 0, f = 1; char ch = getchar();
	while (ch < '0' || ch > '9') {
		if (ch == '-') f = -1;
		ch = getchar();
	}
	while (ch >= '0' && ch <= '9') {
		x = (x << 1) + (x << 3) + (ch ^ 48);
		ch = getchar();
	}
	return x * f;
}
const int N = 2e5 + 10, M = 20;
int n, m, kk;
int a[N], v[N];
int f[N], g[N];
int l[M][N], r[M][N];
void print(int x) {
	for (int i = 0; i <= kk; i++) {
		cout << ((x >> i) & 1);
	}
} 
int main() {
	n = read(), m = read();
	for (int i = 1; i <= n; i++) {
		a[i] = read();
	}
	kk = int(log2(m)) + 1;
	v[0] = m;
	for (int i = 1; i <= kk; i++) {
		v[i] = v[i - 1] / 2;
	}
	int ms = (1 << kk) - 1;
	for (int i = 0; i <= kk; i++) {
		l[i][1] = 1;
		for (int j = 1 + 1; j <= n; j++) {
			if (v[i] >= a[j] - a[j - 1]) l[i][j] = l[i][j - 1];
			else l[i][j] = j;
		}
		r[i][n] = n;
		for (int j = n - 1; j >= 1; j--) {
			if (v[i] >= a[j + 1] - a[j]) r[i][j] = r[i][j + 1];
			else r[i][j] = j;
		}
	}
	memset(g, 0x3f, sizeof(g));
	g[0] = n + 1;
	for (int st = 1; st <= ms; st++) {
		for (int i = 1; i <= kk; i++) {
			if (!(st & (1 << i - 1))) continue;
			f[st] = max(f[st], r[i][min(n, f[st - (1 << i - 1)] + 1)]);
			g[st] = min(g[st], l[i][max(1, g[st - (1 << i - 1)] - 1)]);
		}
	}
	for (int i = 1; i <= n; i = r[0][i] + 1) {
		int flag = 0;
		for (int st = 0; st <= ms; st++) {
			int s = ms - st;
			if (f[st] >= i - 1 && g[s] <= r[0][i] + 1) {
				flag = 1;
				break;
			}
		}
		for (int j = i; j <= r[0][i]; j++) {
			if (flag) printf("Possible\n");
			else printf("Impossible\n");
		}
	}
	
	return 0;
}

T2 数塔(pyramid)

二分答案 \(x\)。考虑将 \(<x\) 的数设成 \(0\)，\(\geq x\) 的设为 \(1\)。现在要求的就是最顶上的数是 \(0\) 还是 \(1\)。

不难发现，如果原 01 序列中有相邻的两个数相同，那么这两个数上面全是这个数。画图有助于理解。

另外一种情况在于没有相邻的相同的数，那这种情况就是两边的数为答案。

#include <bits/stdc++.h>

using namespace std;

int read() {
	int x = 0; char ch = getchar();
	while (ch < '0' || ch > '9') ch = getchar();
	while (ch >= '0' && ch <= '9') {
		x = (x << 1) + (x << 3) + (ch ^ 48);
		ch = getchar();
	}
	return x;
}
const int N = 2e5 + 10;
int n, a[N], b[N];
bool check(int x) {
	for (int i = 1; i <= n; i++) {
		b[i] = (a[i] >= x);
	}
	for (int i = n / 2, j = n / 2 + 2; i >= 1 && j <= n; i--, j++) {
		if (b[i] == b[i + 1]) return b[i];
		if (b[j] == b[j - 1]) return b[j];
	} 
	return b[1];
}
int solve() {
	n = read();
	n = 2 * n - 1;
	for (int i = 1; i <= n; i++) {
		a[i] = read();
	}
	int l = 1, r = n, ans = 0; 
	while (l <= r) {
		int mid = (l + r) / 2;
		if (check(mid)) {
			ans = mid;
			l = mid + 1;
		} else {
			r = mid - 1;
		}
	}
	printf("%d\n", ans);
	
	return 0;
}
int main() {
	int qq = read();
	while (qq--) {
		solve();
	}
	
	return 0;
}

T3 二择(choice)

这题思路也不是那么难，也不知道为什么没人做出来。

我们注意到大小为 \(n\) 的匹配和大小为 \(n\) 的独立集加起来共有 \(3n\) 个点。

考虑求出一组极大匹配（此处不一定非要求最大匹配，一条一条往进加，能加就加），这样剩下来的点集一定是独立集。不难发现，这个匹配和这个独立集必然有至少一个满足条件。

#include <bits/stdc++.h>

using namespace std;

int read() {
	int x = 0; char ch = getchar();
	while (ch < '0' || ch > '9') ch = getchar();
	while (ch >= '0' && ch <= '9') {
		x = (x << 1) + (x << 3) + (ch ^ 48);
		ch = getchar();
	}
	return x;
}
const int N = 1500000 + 10;
int n, m;
int f[N], ans[N], tot;
int solve() {
	n = read(), m = read();
	if (n == 0) {
		printf("Beta1\n");
		return 0;
	}
	for (int i = 1; i <= 3 * n; i++) f[i] = 0;
	tot = 0;
	for (int i = 1; i <= m; i++) {
		int x = read(), y = read();
		if (!f[x] && !f[y]) {
			f[x] = f[y] = 1;
			ans[++tot] = i;
		}
	}
	if (tot >= n) {
		printf("Beta2\n");
		for (int i = 1; i <= n; i++) printf("%d ", ans[i]);
		printf("\n");
	} else {
		printf("Beta1\n");
		tot = 0;
		for (int i = 1; i <= 3 * n; i++) {
			if (!f[i]) ans[++tot] = i, f[i] = 1;
		}
		for (int i = 1; i <= n; i++) printf("%d ", ans[i]);
		printf("\n");
	}
	
	return 0;
}
int main() {
	int qq = read();
	while (qq--) {
		solve();
	}
	
	return 0;
}

T4 平衡(balance)

简单的。

我们注意到要使和的极差不超过 1，那么必然位于 \(i\) 和 \(i+n\) 的两个数差必然为 1。

考虑从 \(i=1\) 和 \(i=n+1\) 同时开始填数。要使 \(i\) 到 \(n\) 和 \(n+1\) 到 \(2n\) 的两段数的和之差不超过 1，考虑让他们的差尽可能小。考虑在前一段中填 1，同时在后一段填 2；在前一段填 4，在后一段填 3；在前一段填 5，在后一段填 6。

这是感性理解。测验大样例后证实了想法。

#include <bits/stdc++.h>

using namespace std;

int read() {
	int x = 0; char ch = getchar();
	while (ch < '0' || ch > '9') ch = getchar();
	while (ch >= '0' && ch <= '9') {
		x = (x << 1) + (x << 3) + (ch ^ 48);
		ch = getchar();
	}
	return x;
}
const int N = 2e5 + 10;
int n;
int ans;
int a[N];
int solve() {
	n = read();
	for (int i = 1; i <= n; i++) {
		if (i % 2 == 1) {
			a[i] = i * 2 - 1;
			a[i + n] = i * 2;
		} else {
			a[i] = i * 2;
			a[i + n] = i * 2 - 1;
		}
	}
	int sum = 0;
	for (int i = 1; i <= n; i++) {
		sum += a[i];
	}
	int mx = sum, mn = sum;
	ans = 1;
	for (int i = 2; i <= 2 * n; i++) {
		sum -= a[i - 1];
		sum += a[(i + n - 1 - 1) % (2 * n) + 1];
		mx = max(mx, sum);
		mn = min(mn, sum);
		if (mx - mn > 1) {
			ans = 0;
			break;
		}
	}
	if (ans) {
		printf("YES\n");
		for (int i = 1; i <= 2 * n; i++) {
			printf("%d ", a[i]);
		}
		printf("\n");
	} else {
		printf("NO\n");
	}
	
	return 0;
}
int main() {
	int qq = read();
	while (qq--) {
		solve();
	}
	
	return 0;
}

小结

这两天的考试暴露出来很多问题。一个是学期内大部分精力投入文化课，导致手感生疏。另外一个是长期不打比赛，对于比赛经验以及做题技巧的运用显得生疏。这些天的比赛起码先回复到比较佳的一个状态。

对于今天的考试而言，还行吧，中规中矩。T1 考虑有纰漏，要是考虑得再详细准确一些，就不会交那个全 Impossible 的 0pts 的代码而是 80pts 的假做法。对于这种诈骗场，极度考验取舍、对题目难度的判断、对时间的分配。

2025CSP-S模拟赛13

怎么感觉这几天都在和数据斗智斗勇。。

T1 马

考试时写了一个神秘贪心，和出题人玩心里博弈。根据我们精湛的骗分技术，也是骗到了 90pts 的高分。

直接来看正解。

有什么可说的。这么简单的 dp 想不出来不就是**。我是**！我是**！我是**！

说一个最简单的思路吧。考虑 \(f_{t,i,j,k}\) 表示考虑到第 \(t\) 匹马，当前三种活动分别满足了 \(i,j,k\) 个人。转移不就是：

\[f_{t,i,j,k}=\min \left\{\begin{array}{ll} f_{t-1,i-1,j,k}+50 \\ f_{t-1,i,j-1,k}+20 \\ f_{t-1,i,j,k-1}\times 2 \end{array}\right\} \]

#include <bits/stdc++.h>

using namespace std;

int read() {
	int x = 0; char ch = getchar();
	while (ch < '0' || ch > '9') ch = getchar();
	while (ch >= '0' && ch <= '9') {
		x = (x << 1) + (x << 3) + (ch ^ 48);
		ch = getchar();
	}
	return x;
}
#define max(x, y) (x > y ? x : y)
#define min(x, y) (x < y ? x : y)
const int INF = 0x3f3f3f3f;
const int N = 150 + 5, M = 300 + 5, K = 100 + 5;
const int maxn = 100;
int n, m, a[5];
int f[2][M][M][M]; 

int main() {
	n = read(), m = read(), a[1] = read(), a[2] = read(), a[3] = read();
	int a1 = a[1], a2 = a[2], a3 = a[3];
	memset(f, 0x3f, sizeof(f));
	int ans = 0;
	int z = 0;
	f[z][0][0][0] = 1;
	for (int id = 1; id <= n; id++) {
		z ^= 1;
		for (int i = 0; i <= a1; i++) {
			for (int j = 0; j <= a2; j++) {
				for (int k = 0; k <= a3; k++) {
					if (f[z ^ 1][i][j][k] <= 100) f[z][i][j][k] = 1;
					else f[z][i][j][k] = INF;
				}
			}
		}
		for (int i = 0; i <= a1; i++) {
			for (int j = 0; j <= a2; j++) {
				for (int k = 0; k <= a3; k++) {
					if (i) f[z][i][j][k] = min(f[z][i][j][k], f[z][i - 1][j][k] + 50);
					if (j) f[z][i][j][k] = min(f[z][i][j][k], f[z][i][j - 1][k] + 20);
					if (k) f[z][i][j][k] = min(f[z][i][j][k], f[z][i][j][k - 1] * 2);
					if (f[z][i][j][k] <= 100) {
						ans = max(ans, i + j + k);
					}
				}
			}
		}
	}
	printf("%d\n", ans);
	
	return 0;
}

T2 可爱捏

懒得写了，直接复制 bobo 的题解。。

初步思路

由于最终的判定条件是两数乘积是否为立方数，所以可以先对所有数预处理——将其所有质因子的次数模 3，这样得到的数质因子指数只能是 1 或 2 方便处理（指数为 3 的倍数的可以忽略），并且可以很好地保持两个数乘积在立方数判定意义下的性质。

首先判掉一些好判的数方便后续处理。如果原数列中出现了立方数，则在集合 S 中他们最多只能出现一个，只需 ans 加 1 然后跳过处理这些数。

然后考虑对于每一个数分解因数后，把每个因子指数模 3 后相乘，处理出一个数 \(x\)。然后我们需要处理出一个数\(y\)，使得 \(x \times y\) 为一个完全立方数。然后，把 \(x\) 和 \(y\) 映射到 map 中。我们称这样的 \(x\) 和 \(y\) 是对应的，则查询是一组对应的数中取出现次数较多的一个即可。

30pts

考虑数据范围，则在根号时间内将所有数质因数分解是可以接受的，在分解的过程中将数以上述思路处理，之后再遍历一遍所有的处理后的数，统计答案，时间复杂度\(O(n\sqrt{a_{i}}+n\log n)\) (用 \(a_{i}\) 代指值域)。

100pts

值域如果是 \(10^{10}\) 在以根号的时间复杂度分解质因数就不可接受了。考虑优化将每一个数 \(a_{i}\) 处理成其对应的 \(x\)（或对应 \(y\)）的过程。考虑只将每一个 \(a_{i}\) 中小于 \(\sqrt[3]{a_{i}}\) 的因子分解出来处理，这样 \(a_{i}\) 就只剩下大于 \(\sqrt[3]{a_{i}}\) 的质因子了，易证他此时剩下的部分 \(m\) 最多只能被分解成两个质因子之积（因为此时小于 \(\sqrt[3]{a_i}\) 的因子已经被分解出去了，所以 \(m\) 的因子都大于 \(\sqrt[3]{a_i}\)，若有多于两个的因子则 \(m\) 的值将会大于 \(a_i\) ）。考虑分类讨论：

  1. \(m = 1\) 此时已经分解完成。
  2. \(m\) 为一个大于 \(\sqrt[3]{a_{i}}\) 的质数，则 \(y\) 为前面求出 \(y\) 的一部分乘上 \(m^2\) (注意如果 \(a_i\) 对应的 \(y\) 大于了 \(10^{10}\) 则可以直接选入 S）。
  3. \(m\) 为两个不同质数相乘 ，情况同2处理，因为质因数质数都为 1。
  4. \(m\)为两个相同质数相乘，则 \(y\) 为前面求出 \(y\) 的一部分乘上 \(\sqrt{m}\)。

之后处理相同，时间复杂度 \(O(n\sqrt[3]{a_{i}}+n\log n)\)。

#include <bits/stdc++.h>
#define int long long

using namespace std;

int read() {
	int x = 0; char ch = getchar();
	while (ch < '0' || ch > '9') ch = getchar();
	while (ch >= '0' && ch <= '9') {
		x = (x << 1) + (x << 3) + (ch ^ 48);
		ch = getchar();
	}
	return x;
}
const int N = 1e5 + 10;
int n, a[N];
unordered_map<int, int> mp, vis;
int b[N], c[N];
signed main() {
	n = read();
	for (int i = 1; i <= n; i++) {
		a[i] = read();
		int x = a[i];
		int num = 1, num1 = 1;
		for (int j = 2; j * j * j <= a[i]; j++) {
			if (x % j == 0) {
				int cnt = 0;
				while (x % j == 0) {
					cnt++;
					x /= j;
				}
				cnt %= 3;
				if (cnt == 1) num *= j, num1 *= j * j;
				if (cnt == 2) num *= j * j, num1 *= j;
			}
		}
		if (x > 1) {
			int xx = sqrt(x);
			if (xx * xx == x) {
				num *= xx * xx;
				num1 *= xx;
			} else {
				num *= x;
				num1 *= x * x;
			}
		}
		mp[num]++;
		b[i] = num, c[i] = num1;
	} 
	int ans = 0;
	for (int i = 1; i <= n; i++) {
		if (vis[b[i]]) continue;
		vis[b[i]] = vis[c[i]] = 1;
		if (b[i] == 1) {
			ans++;
			continue;
		}
		ans += max(mp[b[i]], mp[c[i]]);
	}
	printf("%lld\n", ans);
	
	return 0;
}

T3 诗

有什么可说的！\(n^2\) 过十万！！暴力哈希就可以直接 AC ！！！

#include <bits/stdc++.h>
#define ull unsigned long long

using namespace std;

int read() {
	int x = 0; char ch = getchar();
	while (ch < '0' || ch > '9') ch = getchar();
	while (ch >= '0' && ch <= '9') {
		x = (x << 1) + (x << 3) + (ch ^ 48);
		ch = getchar();
	}
	return x;
}
const int P = 131;
const int N = 1e5 + 10;
int n, qq, op, lastans;
int s[N], t[N];
ull p[N], hsh[N];
inline ull gethsh(int l, int r) {
	return hsh[r] - hsh[l - 1] * p[r - l + 1];
}
int main() {
	op = read(), n = read(), qq = read();
	for (int i = 1; i <= n; i++) {
		s[i] = read();
	}
	p[0] = 1;
	for (int i = 1; i < N; i++) p[i] = p[i - 1] * P;
	for (int i = 1; i <= n; i++) {
		hsh[i] = hsh[i - 1] * P + s[i];
	}
	while (qq--) {
		int len = read();
		ull h = 0;
		for (int i = 1; i <= len; i++) {
			t[i] = read() ^ lastans;
			h = h * P + t[i];
		}
		int ans = 0;
		for (int i = 1; i + len - 1 <= n; i++) {
			ans += (h == gethsh(i, i + len - 1));
		}
		printf("%d\n", ans);		
		if (op) lastans = ans;
	}
	
	return 0;
}

T4 相似

2025CSP-S模拟赛14

T1 魔力屏障

基础思路

首先我们注意到一个东西，就是任何时刻都选择恰好能击破当前屏障的一定是最优的。因为如果当前花费更多代价，后面这部分会减半，还不如在后面在放上多出的这部分。

然后有一个事情，我们从样例中就能看出，从前往后逐个击破不一定是最优的。

依次，我们考虑区间 dp。

考虑 \(f_{i,j,k}\) 表示 \(i\) 到 \(j\) 这段区间击破后还剩一个 \(k\) 的魔力值的攻击，的最小花费。答案即为 \(\min f_{1,i,k}\)。初始化 \(f_{i,i,a[i]/2}=a[i]\)。

考虑转移。效仿经典的区间 dp，考虑枚举断点 \(m\) 以及前一半即 \([i,m]\) 击破后剩余的攻击值 \(v\)，那么后一半即 \([m+1,j]\) 的剩余攻击值即为 \(k-v\)。写下来就是：

\[f_{i,j,k}=\min_{i\le m < j} \min_{0 \le v \le k} \{f_{i,m,v}+f_{m+1,j,k-v}\} \]

然后考虑把剩余的攻击累加到后续的攻击中。不妨设 \([l,r-1]\) 剩余的攻击值为 \(p\)，那么此时击破下一个屏障只需额外花费 \(\max\{0,a_r-p\}\)。简单处理即可。

复杂度分析

可以发现 \(k\) 一定小于等于 \(\sum a_i\)，因为答案至多为 \(\sum a_i\)。

然后考虑到在任意时刻的魔力值一定不会多于当前的 \(a_i\)，类似之前的思考方式，多出的在后面会减半。所以我们在枚举 \(k\) 的时候保证 \(k \le \max a_i\) 即可。

记 \(V=\max a_i\)，时间复杂度为 \(O(n^3V^2)\)。外加带有 \(\frac{1}{8}\) 小常数，可以通过本题。

#include <bits/stdc++.h>

using namespace std;

int read() {
	int x = 0; char ch = getchar();
	while (ch < '0' || ch > '9') ch = getchar();
	while (ch >= '0' && ch <= '9') {
		x = (x << 1) + (x << 3) + (ch ^ 48);
		ch = getchar();
	}
	return x;
}
#define min(x, y) (x < y ? x : y)
#define max(x, y) (x > y ? x : y)
const int INF = 0x3f3f3f3f;
const int N = 70 + 2, M = 150 + 2;
int n, a[N];
int f[N][N][M];
int main() {
	n = read();
	int mx = 0;
	for (int i = 1; i <= n; i++) {
		a[i] = read();
		mx = max(mx, a[i]);
	}
	for (int i = 1; i <= n; i++) 
		for (int j = 1; j <= n; j++) 
			for (int k = 0; k <= mx; k++) 
				f[i][j][k] = INF;
	for (int i = 1; i <= n; i++) {
		f[i][i][a[i] >> 1] = a[i];
	}
	for (int len = 2; len <= n; len++) {
		for (int i = 1; i + len - 1 <= n; i++) {
			int j = i + len - 1;
			for (int k = 0; k <= mx; k++) {
				for (int m = i; m < j; m++) {
					for (int v = 0; v <= k; v++) {
						f[i][j][k] = min(f[i][j][k], f[i][m][v] + f[m + 1][j][k - v]); 
					}
				}
			}
			for (int v = 0; v < a[j]; v++) {
				f[i][j][a[j] >> 1] = min(f[i][j][a[j] >> 1], f[i][j - 1][v] + a[j] - v);
			}
			for (int v = a[j]; v <= mx; v++) {
				f[i][j][v >> 1] = min(f[i][j][v >> 1], f[i][j - 1][v]);
			}
		}
	}
	for (int i = 1; i <= n; i++) {
		int ans = INF;
		for (int k = 0; k <= mx; k++) {
			ans = min(ans, f[1][i][k]);
		}
		printf("%d ", ans);
	}
	
	return 0;
}

T2 诡秘之主

咕

T3 博弈

又是博弈论。这次和上次不一样，起码有个基本的大概思路，虽然没什么用。

直接看正解。

首先考虑以 \(T\) 为根重建树。那么问题转化为要走到根节点。

先考虑存在边 \((S,T)\) 的情况。如果小 Y 不做任何操作的话，那么小 N 的最优策略就是向叶子节点走到底。然后此时小 N 动不了了，小 Y 的最优策略就是通过断边和恢复边把小 N 赶到根节点。

设 \(f_v\) 表示在以 \(v\) 为根的子树中，初始小 N 从 \(v\) 出发，最后被迫回到 \(v\) 的最小代价。考虑在 \(u\) 的子树中，小 N 最优一定是走 \(f_v\) 最大的一个儿子，那么小 Y 就会堵住这个儿子，那么小 N 就会走第二大的。则：

\[f_u=2\text{nd}\max_{v\in son_u} \{1+f_v+|son_u|-1\} \]

这里把 \(-1\) 和 \(+1\) 分开写是便于理解。

现在考虑对于一般情况。一般情况下，小 N 会先向根的方向走一段距离，再向叶子的方向走。

考虑将最优化问题转化为判定问题。现在钦定一个小 Y 的总操作次数 \(M\)，看能否在 \(M\) 次内结束博弈（把小 N 赶到根节点）。

考虑用 \(g_u\) 表示从 \(u\) 到根节点一路上分岔路的数量（不记根链）。\(f\) 和 \(g\) 都可以通过一次 dfs 得到。

现在，我们模拟从 \(S\) 走到根的过程。当位于点 \(u\) 的时候，如果有一个儿子 \(v \in son_u\)，使得 \(g_u+f_v+cnt>M\)（其中 \(cnt\) 为此前的操作次数），即如果小 N 从 \(v\) 走下去我们再把他赶上来的总代价大于总操作次数，那么就一定不能让他从 \(v\) 走，于是就要把 \((u,v)\) 这条边断掉。

当当前的操作次数大于总操作次数时或大于可操作次数时（由于两人时轮流操作的），不合法。

没了。

然后就是由于每条边最多被删一次加一次，所以最多操作 \(2n\) 次。

显然 \(M\) 是具有单调性的，所以可以使用二分答案。时间复杂度 \(O(n\log n)\)。

#include <bits/stdc++.h>

using namespace std;

int read() {
	int x = 0; char ch = getchar();
	while (ch < '0' || ch > '9') ch = getchar();
	while (ch >= '0' && ch <= '9') {
		x = (x << 1) + (x << 3) + (ch ^ 48);
		ch = getchar();
	}
	return x;
}
const int P = 131;
const int INF = 0x3f3f3f3f;
const int N = 1e6 + 10;
int n, T, S;
vector<int> G[N];
int f[N], g[N], fa[N], dep[N];
void dfs(int x, int father) {
	fa[x] = father;
	dep[x] = dep[fa[x]] + 1;
	if (fa[x] != 0) g[x] = g[fa[x]] + (G[x].size() - 2);
	int mx = 0, mxx = 0;
	for (int y : G[x]) {
		if (y == fa[x]) continue;
		dfs(y, x);
		if (f[y] > mx) {
			mxx = mx;
			mx = f[y];
		} else if (f[y] > mxx) {
			mxx = f[y];
		}
	}
	f[x] = mxx + (G[x].size() - (fa[x] != 0));
}
bool check(int ops) {
	int cnt = 0, lst = -1;	// cnt 是当前操作次数
	int tim = 0;			// tim 是当前可操作次数
	for (int x = S; x != T; x = fa[x]) {
		tim++;
		int tmp = cnt;
		for (int y : G[x]) {
			if (y != lst && y != fa[x] && g[x] + f[y] + tmp + (lst == -1) > ops) {
				cnt++;
			}
		}
		if (cnt > tim || cnt > ops) return false;
		lst = x;
	}
	return true;
}
int main() {
	n = read(), T = read(), S = read();
	if (T == S || n <= 2) {
		printf("0\n");
		return 0;
	}
	for (int i = 1; i < n; i++) {
		int x = read(), y = read();
		G[x].push_back(y);
		G[y].push_back(x);
	}
	dfs(T, 0);
	int l = 0, r = 2 * n, ans = 0;
	while (l <= r) {
		int mid = l + r >> 1;
		if (check(mid)) {
			ans = mid;
			r = mid - 1;
		} else {
			l = mid + 1;
		}
	}
	printf("%d\n", ans);
	
	return 0;
}

T4 地雷

这个区间 dp 还是很牛逼了。

直接来看正解。

考虑区间 dp。设 \(f_{i,j,t,u}\) 表示当前考虑区间 \([i,j]\)，满足 \(i-1,j-1\) 都比 \([i,j]\) 更晚删除，在 \(j+1\) 后第一个比 \([i,j]\) 更晚删除的数的下标是 \(t\)。同时，\(u\) 是一些限制条件，需要保证区间中 \(u\) 左侧的数都比 \(u\) 更早删除，\(u \in[i,j+1]\)。\(f\) 就是满足上述条件的区间 \([i,j]\) 的最大删除代价。

枚举 \(k \in[i,j]\)，枚举对于 \(k\) 而言左侧区间的 \(t\)（设为 \(v\)），根据 \(u\) 的定义，\(k\) 必须 \(\geq u\)。\(v\in[k+1,j+1]\)。

综上，整理出来一个图，反映数（区间）大致的空间分布以及被删除顺序：

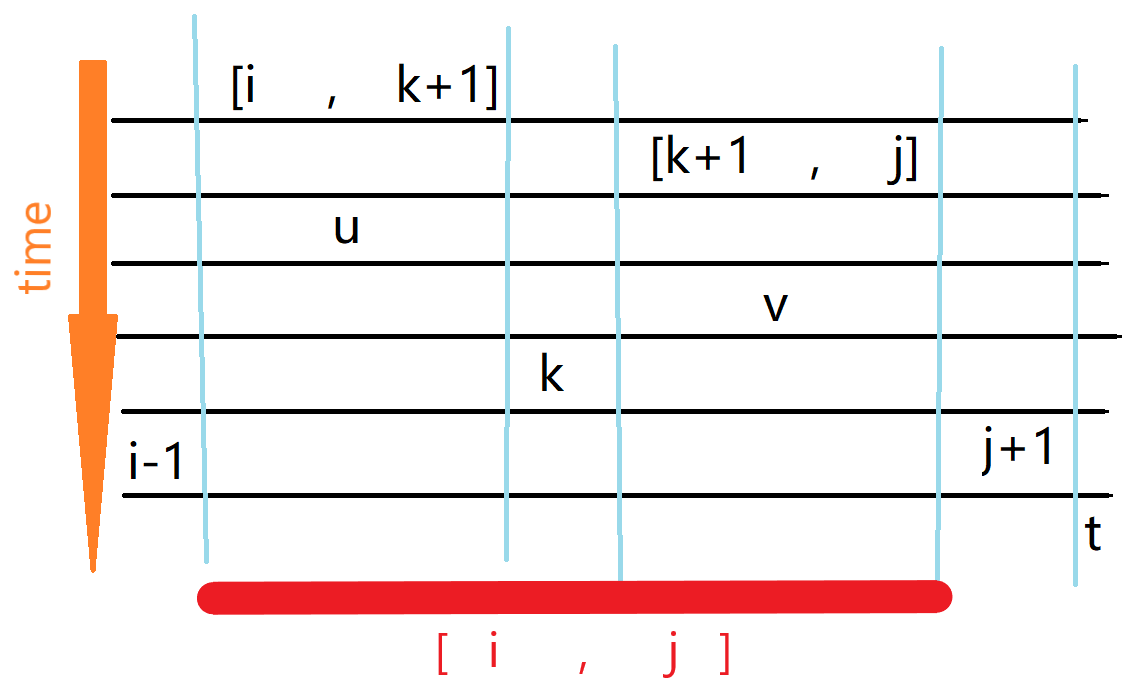
image

转移：

\[f_{i,j,t,u}=\max_{u\le k\le j,k+1\le v \le j+1}\{f_{i,k-1,v,u}+f_{k+1,j,t,v}+val(i-1,k,j+1,t)\} \]

其中

\[val(a,b,c,d)=(p_a-q_b)^2+(p_b-r_c)^2+(p_c-s_d)^2 \]

那就是这样。题解还有一堆解释，我觉得没必要了，这一个图就很清晰了。

这里附上题解剩下的话：

image

#include <bits/stdc++.h>

using namespace std;

int read() {
	int x = 0, f = 1; char ch = getchar();
	while (ch < '0' || ch > '9') {
		if (ch == '-') f = -1;
		ch = getchar();
	}
	while (ch >= '0' && ch <= '9') {
		x = (x << 1) + (x << 3) + (ch ^ 48);
		ch = getchar();
	}
	return x * f;
}
const int INF = 0x3f3f3f3f;
const int N = 70 + 5;
int n, p[N], q[N], r[N], s[N];
int f[N][N][N][N];
inline int S(int x) {
	return x * x;
}
inline int solve(int a, int b, int c, int d) {
	return S(p[a] - q[b]) + S(p[b] - r[c]) + S(p[c] - s[d]);
}
int main() {
	n = read();
	for (int i = 1; i <= n; i++) p[i] = read();
	for (int i = 1; i <= n; i++) q[i] = read();
	for (int i = 1; i <= n; i++) r[i] = read();
	for (int i = 1; i <= n; i++) s[i] = read();
	for (int i = 0; i < N; i++)
		for (int j = 0; j < N; j++) 
			for (int t = 0; t < N; t++)
				for (int u = 0; u < N; u++) f[i][j][t][u] = -INF;
	for (int i = 1; i <= n + 2; i++) {
		for (int t = i + 2; t <= n + 2; t++) {
			f[i][i][t][i] = f[i][i][t][i + 1] = solve(i - 1, i, i + 1, t);
		} 
		for (int t = i + 1; t <= n + 2; t++) {
			f[i][i - 1][t][i] = 0;
		}
	}
	for (int len = 2; len <= n; len++) {
		for (int i = 1; i + len - 1 <= n; i++) {
			int j = i + len - 1;
			for (int t = j + 2; t <= n + 2; t++) {
				for (int u = i; u <= j + 1; u++) {
					for (int k = u; k <= j; k++) {
						int val = solve(i - 1, k, j + 1, t);
						int x = (u == k ? i : u);
						f[i][j][t][u] = max(f[i][j][t][u], f[i][k - 1][j + 1][x] + f[k + 1][j][t][k + 1] + val);
						for (int v = k + 1; v <= j + 1; v++) {
							f[i][j][t][u] = max(f[i][j][t][u], f[i][k - 1][v][x] + f[k + 1][j][t][v] + val);
						}
					}
				}
			}
		}
	}
	printf("%d\n", f[1][n][n + 2][1]);
	
	return 0;
}

2025CSP-S模拟赛15

T1 万花筒

这个题其实考试时想得差不多了。

简单写了。将边从小到大排序。令 \(d=|u-v|\)，那么加入这些边（即 \((u+k,v+k)\)）后，会产生 \(\gcd(m,d)\) 个连通块，其中 \(m\) 为加入这些边前连通块的数量。当连通块总数为 1 时输出总代价，然后就没了。

#include <bits/stdc++.h>
#define int long long

using namespace std;

int read() {
	int x = 0; char ch = getchar();
	while (ch < '0' || ch > '9') ch = getchar();
	while (ch >= '0' && ch <= '9') {
		x = (x << 1) + (x << 3) + (ch ^ 48);
		ch = getchar();
	}
	return x;
}
const int INF = 0x3f3f3f3f3f3f3f3f;
const int N = 1e9 + 10, M = 1e5 + 10;
int n, m;
struct node {
	int x, y, w;
	bool operator < (const node & cmp) const {
		return w < cmp.w;
	}
} e[M];
int d[M], w[M];
int gcd(int n, int m) {
	return m == 0 ? n : gcd(m, n % m);
}
int solve() {
	n = read(), m = read();
	for (int i = 1; i <= m; i++) {
		e[i] = {read(), read(), read()};
	}
	sort(e + 1, e + 1 + m);
	int ans = 0;
	for (int i = 1; i <= m; i++) {
		int d = abs(e[i].x - e[i].y);
		int num = n - gcd(n, d);
		if (num > 0) {
			ans += num * e[i].w;
			n = gcd(n, d);
		}
	}
	printf("%lld\n", ans);
	
	return 0;
}
signed main() {
	int qq = read();
	while (qq--) {
		solve();
	}
	
	return 0;
}

T2 冒泡排序趟数期望

考虑对于排列 \(p[i]\)，定义 \(inv[i]=\sum[j<i \and p[j]>p[i]]\)，不难得出 \(res=\max inv[i]\)。

然后我们可以发现，\(inv[i] \in [0,i-1]\)，所以不同的 \(inv\) 数组共有 \(n!\) 个，恰好和所有排列一一对应。依此，问题可以转化为求 \(\max inv[i]=k\) 的方案数。

考虑构造合法的 \(inv\) 数组。要使构造的 \(inv\) 最大值为 \(k\)，则：对于 \(i \le k\) 的位置随便取，\(i>k\) 的位置 \(<k\) 且至少有一个 \(k\)。方案数即为：

\[cnt[k]=k!((k+1)^{n-k}-k^{n-k}) \]

答案即为 \(\frac{\sum k\times cnt[k]}{n!}\)。

#include <bits/stdc++.h>
#define int long long

using namespace std;

int read() {
	int x = 0; char ch = getchar();
	while (ch < '0' || ch > '9') ch = getchar();
	while (ch >= '0' && ch <= '9') {
		x = (x << 1) + (x << 3) + (ch ^ 48);
		ch = getchar();
	}
	return x;
} 
const int MOD = 1e9 + 7;
const int N = 1e6 + 10;
int n, fact[N];
int fpow(int a, int x) {
	a %= MOD;
	int ans = 1;
	while (x) {
		if (x & 1) ans = ans * a % MOD;
		a = a * a % MOD;
		x >>= 1;
	}
	return ans;
}
int ans = 0;
int a[N];
signed main() {
	n = read();
	fact[0] = 1;
	for (int i = 1; i <= n; i++) fact[i] = fact[i - 1] * i % MOD;
	int ans = 0;
	for (int i = 0; i < n; i++) {
		ans = (ans + (fact[i] * (fpow(i + 1, n - i) - fpow(i, n - i) + MOD) % MOD) % MOD * i % MOD) % MOD;
	}
	ans = ans * fpow(fact[n], MOD - 2) % MOD;
	printf("%lld\n", ans);
	
	return 0;
}

T3 数点

T4 精shen细腻

2025CSP-S模拟赛16

T1 醉

简单题。也是场切了。

首先考虑答案是否存在。根据一个性质叫做一个点在树上离他最远的节点一定是直径的端点。记直径为端点分别为 \(U,V\)。然后分别算一下点 \(u\) 和 \(U,V\) 的距离是否 \(\geq d\) 即可。

考虑存在答案，那么不妨设 \(dis(u,U) \geq d\)，则点 \(v\) 一定在 \(u\) 到 \(U\) 的这条路径上。然后就做完了。求出 \(u\) 和 \(U\) 的 lca 记为 \(lca\)，判断 \(v\) 在 \(u,lca\) 的路径上还是在 \(U,lca\) 的路径上，然后跳 \(k\) 级祖先就行了。

#include <bits/stdc++.h>

using namespace std;

int read() {
	int x = 0; char ch = getchar();
	while (ch < '0' || ch > '9') ch = getchar();
	while (ch >= '0' && ch <= '9') {
		x = (x << 1) + (x << 3) + (ch ^ 48);
		ch = getchar();
	}
	return x;
}
const int N = 2e5 + 10;
int n, m;
vector<int> G[N];
int dep[N], fa[N][22];
int U, V, dd[N];
void dfs1(int x, int fr) {
	dep[x] = dep[fr] + 1;
	if (dep[x] > dep[U]) U = x;
	fa[x][0] = fr;
	for (int i = 1; i <= 20; i++) {
		fa[x][i] = fa[fa[x][i - 1]][i - 1];
	}
	for (int y : G[x]) {
		if (y == fr) continue;
		dfs1(y, x);
	}
}
void dfs2(int x, int fr) {
	dd[x] = dd[fr] + 1;
	if (dd[x] > dd[V]) V = x;
	for (int y : G[x]) {
		if (y == fr) continue;
		dfs2(y, x);
	}
}
int getlca(int x, int y) {
	if (dep[x] < dep[y]) swap(x, y);
	for (int i = 20; i >= 0; i--) {
		if (dep[fa[x][i]] >= dep[y]) x = fa[x][i];
	}
	if (x == y) return x;
	for (int i = 20; i >= 0; i--) {
		if (fa[x][i] != fa[y][i]) {
			x = fa[x][i];
			y = fa[y][i];
		}
	}
	return fa[x][0];
}
inline int getdis(int x, int y) {
	return dep[x] + dep[y] - 2 * dep[getlca(x, y)];
}
int getfa(int x, int k) {
	for (int i = 0; i <= 20; i++) {
		if ((k >> i) & 1) {
			x = fa[x][i];
		}
	}
	return x;
}
int main() {
	n = read();
	for (int i = 1; i < n; i++) {
		int x = read(), y = read();
		G[x].push_back(y);
		G[y].push_back(x);
	}
	dfs1(1, 0);
	dfs2(U, 0);
	m = read();
	while (m--) {
		int u = read(), d = read();
		int d1 = getdis(u, U), d2 = getdis(u, V);
		if (d1 < d && d2 < d) {
			printf("-1\n");
			continue;
		}
		if (d1 >= d) {
			int lca = getlca(u, U);
			if (d <= dep[u] - dep[lca]) {
				printf("%d\n", getfa(u, d));
			} else {
				printf("%d\n", getfa(U, d1 - d));
			}
		} else {
			int lca = getlca(u, V);
			if (d <= dep[u] - dep[lca]) {
				printf("%d\n", getfa(u, d));
			} else {
				printf("%d\n", getfa(V, d2 - d));
			}
		}
	}
	
	return 0;
}

T2 与

首先，考虑答案如何求解。不难想到可以用如下方法求解：

for (int i = 1; i <= qq; i++) {
    int l = read(), r = read();
    int sum = a[l];
    for (int i = l + 1; i <= r; i++) {
        if (a[i] & sum) sum |= a[i];
    }
    if (a[r] & sum) printf("Shi\n");
    else printf("Fou\n");
}

然后发现这个满足结合律，考虑用线段树维护。

这个代码不难理解，直接看代码吧。。

#include <bits/stdc++.h>

using namespace std;

int read() {
	int x = 0; char ch = getchar();
	while (ch < '0' || ch > '9') ch = getchar();
	while (ch >= '0' && ch <= '9') {
		x = (x << 1) + (x << 3) + (ch ^ 48);
		ch = getchar();
	}
	return x;
}
const int N = 3e5 + 10;
int n, qq, a[N];
struct node {
	int l, r, s[20];
} tree[4 * N];
#define lc p << 1
#define rc p << 1 | 1
void pushup(int p) {
	for (int i = 0; i < 20; i++) {
		tree[p].s[i] = tree[lc].s[i];
		for (int j = 0; j < 20; j++) {
			if ((1 << j) & tree[lc].s[i]) {
				tree[p].s[i] |= tree[rc].s[j];
			}
		}
		tree[p].s[i] |= tree[rc].s[i];
	}
}
void build(int p, int l, int r) {
	tree[p].l = l, tree[p].r = r;
	if (l == r) {
		for (int i = 0; i < 20; i++) {
			if ((1 << i) & a[l]) tree[p].s[i] = a[l];
		}
		return;
	}
	int mid = l + r >> 1;
	build(lc, l, mid), build(rc, mid + 1, r);
	pushup(p);
}
int sum;
bool query(int p, int l, int r, int v) {
	if (sum & v) return 1;
	if (l <= tree[p].l && tree[p].r <= r) {
		int x = 0;
		for (int i = 0; i < 20; i++) {
			if ((1 << i) & sum) x |= tree[p].s[i];
		}
		sum |= x;
		return sum & v;
	}
	int mid = tree[p].l + tree[p].r >> 1;
	int res = 0;
	if (l <= mid) res |= query(lc, l, r, v);
	if (res) return 1;
	if (mid < r) res |= query(rc, l, r, v);
	return res;
}
int main() {
	n = read(), qq = read();
	for (int i = 1; i <= n; i++) {
		a[i] = read();
	}
	build(1, 1, n);
	for (int i = 1; i <= qq; i++) {
		int l = read(), r = read();
		sum = a[l];
		if (query(1, l + 1, r - 1, a[r])) {
			printf("Shi\n");
		} else printf("Fou\n");
	}
	
	return 0;
}

T3 小恐龙

T4 愤怒的小 L

2025CSP-S模拟赛17

T1 zzy 的金牌

考虑如何判断一个可重集 \(\{s_1,s_2,\dots s_n\}\) 是否可能成为答案，这个可以贪心：将 \(s\) 与 \(a\) 分别从小到大排序后，若 \(\forall i,s_i \geq a_i\) 且 \(\sum s - \sum a=k\) 则合法。于是乎所求即为 \(b_1,b_2,\dots b_n\) 的数量，其中 \(b\) 满足 \(b_i+a+i \geq b_{i-1}+a_{i-1}\) 且 \(\sum b_i=k\)。

考虑设计 dp：\(f_{i,j,k}\) 表示 \(b\) 的前 \(i\) 项有多少种填法满足 \(b_i=j\) 且 \((\sum_{x\le i}b_x)=k\)。转移很简单，\(f_{i,j,k}\rightarrow f_{i+1,l,k+l}(l+a_{i+1} \geq j+a_i)\)。

此时的时间复杂度来到 \(O(nk^3)\)。

考虑令 \(g_{i,k-j,j}=f_{i,j,k}\)，则 \(g_{i,k-j,j}\rightarrow g_{i+1,k,l}(l+a_{i+1} \geq j+a_i)\)。容易发现这是对 \(g_{i+1,k}\) 的一个后缀加，差分维护即可。

时间复杂度 \(O(nk^2)\)。

#include <bits/stdc++.h>
#define int long long
#define ull unsigned long long

using namespace std;

int read() {
	int x = 0; char ch = getchar();
	while (ch < '0' || ch > '9') ch = getchar();
	while (ch >= '0' && ch <= '9') {
		x = (x << 1) + (x << 3) + (ch ^ 48);
		ch = getchar();
	}
	return x;
}
const int P = 131;
const int MOD = 998244353;
const int N = 300 + 10;
int n, kk, a[N];
int f[N][N][N]; 
signed main() {
	n = read(), kk = read();
	for (int i = 1; i <= n; i++) {
		a[i] = read();
	}
	sort(a + 1, a + 1 + n);
	f[0][0][0] = 1;
	for (int i = 0; i <= n; i++) {
		for (int k = 0; k <= kk; k++) {
			for (int j = 0; j <= k; j++) {
				if (!f[i][k - j][k]) continue;
				int l = max(0ll, a[i] + j - a[i + 1]), r = kk - k;
				if (l <= r) {
					(f[i + 1][k][k + l] += f[i][k - j][k]) %= MOD;
					((f[i + 1][k][k + r + 1] -= f[i][k - j][k]) += MOD) %= MOD;
				}
			}
			for (int j = 0; j <= kk; j++) {
				(f[i + 1][k][j + 1] += f[i + 1][k][j]) %= MOD;
			}
		}
	}
	int ans = 0;
	for (int j = 0; j <= kk; j++) {
		(ans += f[n][j][kk]) %= MOD;
	}
	printf("%lld\n", ans);
	
	return 0;
}

T2 口粮输送

T3 作弊

T4 合作的力量

2025CSP-S模拟赛 18

前几天题改的不是很好，先空着。

然后就是今天学习了比较牛逼的快读快写。计划是以后写题把这种读写和 ios 都打上，以备不时之需。

另外一个就是以后比赛总结写得简洁一些，这只不过是一个复盘的过程，又不是写题解。

T1 flandre

可以证明，答案最优一定是取他的一段后缀。这个举几个例子就可以说明。

然后一次考虑每一个后缀，维护答案即可。

#include <bits/stdc++.h>
#define int long long

using namespace std;

int read() {
	int x = 0, f = 1; char ch = getchar();
	while (ch < '0' || ch > '9') {
		if (ch == '-') f = -1;
		ch = getchar();
	}
	while (ch >= '0' && ch <= '9') {
		x = (x << 1) + (x << 3) + (ch ^ 48);
		ch = getchar();
	}
	return x * f;
}
const int INF = 0x3f3f3f3f3f3f3f3f;
const int N = 1e6 + 10;
int n, kk;
struct node {
	int a, id;
	bool operator < (const node & cmp) const {
		return a < cmp.a;
	}
} e[N];
unordered_map<int, int> len;
signed main() {
	n = read(), kk = read();
	for (int i = 1; i <= n; i++) {
		e[i].a = read();
		e[i].id = i;
	}
	sort(e + 1, e + 1 + n);
	int ans = -INF, id = 1;
	int now = 0;
	for (int i = n; i >= 1; i--) {
		now += e[i].a + kk * (n - i - len[e[i].a]);
		len[e[i].a]++;
		if (now > ans) {
			ans = now;
			id = i;
		}
	}
	printf("%lld %lld\n", ans, n - id + 1);
	for (int i = id; i <= n; i++) {
		printf("%lld ", e[i].id);
	}
	
	return 0;
}

T2 meirin

这题场上切了。

考虑拆贡献。考虑每个 \(b_i\) 对于答案的贡献：

\[\begin{array}{ll} ans & = & \sum_{l=1}^n\sum_{r=l}^n(\sum_{i=l}^ra_i)\times(\sum_{i=l}^rb_i) \\ & = & \sum_{i=1}^nb_i(\sum_{l=1}^i\sum_{r=i}^n\sum_{j=l}^ra_j)\\ & = & \sum_{i=1}^nb_i(\sum_{l=1}^i\sum_{r=i}^n(sa_r-sa_{l-1}))\\ & = & \sum_{i=1}^nb_i((\sum_{l=1}^i\sum_{r=i}^nsa_r)-(\sum_{l=1}^i\sum_{r=i}^nsa_{l-1}))\\ & = & \sum_{i=1}^nb_i((i\sum_{r=i}^nsa_r)-((n-i+1)\sum_{l=0}^{i-1}sa_l))\\ \end{array} \]

其中 \(sa_i\) 为 \(a\) 的前缀和。

令 \(f_i\) 表示 \(b_i\) 后面这一坨，即 \(f_i=(i\sum_{r=i}^nsa_r)-((n-i+1)\sum_{l=0}^{i-1}sa_l)\)。如何求？给 \(sa\) 求个前缀和即可 \(O(n)\) 求出。则：

\[ans=\sum_{i=1}^nf_ib_i \]

每次修改给 \(l\) 到 \(r\) 的 \(b_i\) 加上 \(k\)，则答案增加的值即为 \(k\sum_{i=l}^rf_i\)。对 \(f_i\) 求前缀和即可每次操作 \(O(1)\) 修改。

#include <bits/stdc++.h>
#define int long long

using namespace std;

namespace IO {
	const int bufsz = 1 << 20;
	char ibuf[bufsz], *p1 = ibuf, *p2 = ibuf;
	char obuf[bufsz], *p3 = obuf, stk[50];
	#define getchar() (p1 == p2 && (p2 = (p1 = ibuf) + fread(ibuf, 1, bufsz, stdin), p1 == p2) ? EOF : *p1++)
	#define flush() (fwrite(obuf, 1, p3 - obuf, stdout), p3 = obuf)
	#define putchar(ch) (p3 == obuf + bufsz && flush(), *p3++ = (ch))
	inline int read() {
		int x = 0; char ch = getchar(); bool t = 0;
		while (ch < '0' || ch > '9') {t ^= ch == '-'; ch = getchar();}
		while (ch >= '0' && ch <= '9') {x = (x << 1) + (x << 3) + (ch ^ 48); ch = getchar();}
		return t ? -x : x;
	}
	inline void write(int x, bool t = 1) {
		int top = 0;
		do {stk[++top] = x % 10 | 48; x /= 10;} while (x);
		while (top) putchar(stk[top--]);
		t ? putchar('\n') : putchar(' ');
	}
	struct FL {~FL() {flush();}} fl;
	#undef getchar()
	#undef putchar()
	#undef flush()
}
using IO::read;
using IO::write;
const int MOD = 1e9 + 7;
const int N = 5e5 + 10;
int n, qq, a[N], b[N];
int s[N], f[N], ss[N], sf[N];
signed main() {
	n = read(), qq = read();
	for (int i = 1; i <= n; i++) a[i] = read();
	for (int i = 1; i <= n; i++) b[i] = read();	
	for (int i = 1; i <= n; i++) {
		s[i] = (s[i - 1] + a[i]) % MOD;
		ss[i] = (ss[i - 1] + s[i]) % MOD;
	}
	for (int i = 1; i <= n; i++) {
		f[i] = ((ss[n] - ss[i - 1]) % MOD * i % MOD - ss[i - 1] * (n - i + 1) % MOD) % MOD;
		sf[i] = (sf[i - 1] + f[i]) % MOD;
	}
	int ans = 0;
	for (int i = 1; i <= n; i++) {
		ans = (ans + b[i] * f[i] % MOD) % MOD;
	}
	while (qq--) {
		int l = read(), r = read(), k = read();
		ans = (ans + (sf[r] - sf[l - 1]) % MOD * k % MOD) % MOD;
		write((ans + MOD) % MOD);
	}
	
	return 0;
}

T3 sakuya

考虑拆贡献。

考虑每条边对于答案的贡献。首先树形 dp 求出初始的贡献，即为 \(w_i\times num_i\)。其中 \(w\) 为边权，\(num\) 为这条边左右特殊点个数的乘积。然后当一条边的边权加上 \(k\)，对答案增加的贡献即为 \(k\times num_i\)。对于每个点统计发出的所有边的 \(num\) 然后 \(O(1)\) 进行维护答案即可。

#include <bits/stdc++.h>
#define int long long

using namespace std;

namespace IO { 
// 这里的读写这么怪是因为当时数据锅了，快读过不了，只有 cin cout 能过，方便调试。不必在意。
	inline int read() {
		int x;
		cin >> x;
		return x;
	}
	inline void write(int x, bool t = 1) {
		cout << x << '\n';
	}
}
using IO::read;
using IO::write;
const int MOD = 998244353;
const int N = 5e5 + 10;
int n, m, qq, a[N];
struct edge {
	int y, w;
};
vector<edge> G[N];
int fpow(int a, int x) {
	a %= MOD;
	int ans = 1;
	while (x) {
		if (x & 1) ans = ans * a % MOD;
		a = a * a % MOD;
		x >>= 1;
	}
	return ans;
}
int fact[N];
int fa[N];
int f[N], g[N], dp[N], ans;
void dfs(int x, int father) {
	fa[x] = father;
	for (edge i : G[x]) {
		int y = i.y;
		if (y == fa[x]) continue;
		dfs(y, x);
		f[x] += f[y];
		ans = (ans + g[y] * i.w % MOD) % MOD;
		dp[x] = (dp[x] + g[y]) % MOD;
	}
	g[x] = f[x] * (m - f[x]) % MOD * 2 % MOD * fact[m - 1] % MOD;
	dp[x] = (dp[x] + g[x]) % MOD;
}
signed main() {
	ios::sync_with_stdio(0); cin.tie(0), cout.tie(0);
	n = read(), m = read();
	for (int i = 1; i < n; i++) {
		int x = read(), y = read(), z = read();
		G[x].push_back({y, z});
		G[y].push_back({x, z});
	}
	for (int i = 1; i <= m; i++) {
		a[i] = read();
		f[a[i]] = 1;
	}
	fact[0] = 1;
	for (int i = 1; i <= m; i++) fact[i] = fact[i - 1] * i % MOD;
	int ny = fpow(fact[m], MOD - 2);
	dfs(1, 0);
	ans = (ans + MOD) % MOD;
	qq = read();
	while (qq--) {
		int x = read(), k = read();
		ans = (ans + dp[x] * k % MOD) % MOD;
		write(ans * ny % MOD);
	}
	
	return 0;
}

T4 红楼 ~ Eastern Dream

一眼根号分治。

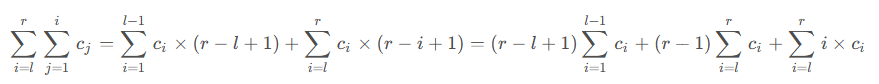
image

image

image

懒得写了，直接截图。

#include <bits/stdc++.h>
#define il inline
#define int long long

using namespace std;

namespace IO {
	const int bufsz = 1 << 20;
	char ibuf[bufsz], *p1 = ibuf, *p2 = ibuf;
	char obuf[bufsz], *p3 = obuf, stk[50];
	#define getchar() (p1 == p2 && (p2 = (p1 = ibuf) + fread(ibuf, 1, bufsz, stdin), p1 == p2) ? EOF : *p1++)
	#define flush() (fwrite(obuf, 1, p3 - obuf, stdout), p3 = obuf)
	#define putchar(ch) (p3 == obuf + bufsz && flush(), *p3++ = (ch))
	inline int read() {
		int x = 0; char ch = getchar(); bool t = 0;
		while (ch < '0' || ch > '9') {t ^= ch == '-'; ch = getchar();}
		while (ch >= '0' && ch <= '9') {x = (x << 1) + (x << 3) + (ch ^ 48); ch = getchar();}
		return t ? -x : x;
	}
	inline void write(int x, bool t = 1) {
		int top = 0;
		do {stk[++top] = x % 10 | 48; x /= 10;} while (x);
		while (top) putchar(stk[top--]);
		t ? putchar('\n') : putchar(' ');
	}
	struct FL {~FL() {flush();}} fl;
	#undef getchar()
	#undef putchar()
	#undef flush()
}
using IO::read;
using IO::write;
const int N = 2e5 + 10, M  = 500;
int n, m, a[N], sq;
int s[N];
int v[M][M], sv[M][M], c[N], ic[N];
int st[M], ed[M], beg[N], cc[N], icc[N];
il void init() {
	for (int i = 1; i <= sq; i++) {
		st[i] = n / sq * (i - 1) + 1;
		ed[i] = n / sq * i;
	}
	ed[sq] = n;
	for (int i = 1; i <= sq; i++) {
		for (int j = st[i]; j <= ed[i]; j++) {
			beg[j] = i;
		}
	}
}
il void update(int p, int x) {
	c[p] += x;
	cc[beg[p]] += x;
	ic[p] += x * p;
	icc[beg[p]] += x * p;
}
il int query(int l, int r) {
	if (l > r) return 0;
	if (beg[l] == beg[r]) {
		int res = 0;
		for (int i = l; i <= r; i++) res += c[i];
		return res;
	}
	int res = 0;
	for (int i = l; i <= ed[beg[l]]; i++) res += c[i];
	for (int i = st[beg[r]]; i <= r; i++) res += c[i];
	for (int i = beg[l] + 1; i < beg[r]; i++) {
		res += cc[i];
	}
	return res;
}
il int queryi(int l, int r) {
	if (l > r) return 0;
	if (beg[l] == beg[r]) {
		int res = 0;
		for (int i = l; i <= r; i++) res += ic[i];
		return res;
	}
	int res = 0;
	for (int i = l; i <= ed[beg[l]]; i++) res += ic[i];
	for (int i = st[beg[r]]; i <= r; i++) res += ic[i];
	for (int i = beg[l] + 1; i < beg[r]; i++) {
		res += icc[i];
	}
	return res;
}
signed main() {
	n = read(), m = read();
	for (int i = 1; i <= n; i++) a[i] = read();
	for (int i = 1; i <= n; i++) s[i] = s[i - 1] + a[i];
	sq = sqrt(n);
	init();
	while (m--) {
		int op = read();
		if (op == 1) {
			int x = read(), y = read(), k = read();
			y = min(x - 1, y);
			if (x <= sq) {
				for (int i = 0; i <= y; i++) {
					v[x][i] += k;
				}
				sv[x][0] = v[x][0];
				for (int i = 1; i < x; i++) {
					sv[x][i] = sv[x][i - 1] + v[x][i];
				}
			} else {
				for (int i = 1; i <= n; i += x) {
					update(i, k);
					update(min(n + 1, i + y + 1), -k);
				}
			}
		} else {
			int l = read(), r = read();
			int ans = s[r] - s[l - 1];
			for (int i = 1; i <= sq; i++) {
				ans += sv[i][(r - 1) % i];
				ans -= sv[i][(l - 1) % i - 1];
				int ll = (l - 1) / i, rr = (r - 1) / i;
				ans += (rr - ll) * sv[i][i - 1];
			}
			ans += (r - l + 1) * query(1, l - 1) + (r + 1) * query(l, r) - queryi(l, r);
			printf("%lld\n", ans);
		}
	}
	
	return 0;
}

2025CSP-S模拟赛20

我觉得还是加个分数比较好。。

T1 T2 T3 T4
0 0 20 0

排名：21/21；总分：20

今日神秘挂分。T1 交错代码挂了 50pts，T2 快写写炸了挂了 20pts。教训：不要快写了！有一种说法快写还没 printf 快！

T1 签

非常神秘。

考虑要合法需要满足两个条件：

  1. 奇数位上全是奇数，偶数位上全是偶数。这个是好理解的。
  2. 奇数位组成的序列的逆序对数量和偶数位组成的序列的逆序对数量之和是原序列的逆序对数量的三分之一。证明：对于一次操作而言，原序列逆序对数会减少 3，相应的奇数位序列逆序对数减少 1，或偶数位序列逆序对数减少 1。

然后就做完了。随便怎么统计一下就完

#include <bits/stdc++.h>
#define il inline
#define int long long

using namespace std;

namespace IO {
	const int bufsz = 1 << 20;
	char ibuf[bufsz], *p1 = ibuf, *p2 = ibuf;
	#define getchar() (p1 == p2 && (p2 = (p1 = ibuf) + fread(ibuf, 1, bufsz, stdin), p1 == p2) ? EOF : *p1++)
	il int read() {
		int x = 0; char ch = getchar(); bool t = 0;
		while (ch < '0' || ch > '9') {t ^= ch == '-'; ch = getchar();}
		while (ch >= '0' && ch <= '9') {x = (x << 1) + (x << 3) + (ch ^ 48); ch = getchar();}
		return t ? -x : x;
	}
	#undef getchar()
}
using IO::read;
const int N = 3e5 + 10;
int n, a[N];
namespace BIT {
	int c[N];
	il void init() {
		for (int i = 1; i <= n; i++) c[i] = 0;
	}
	il void update(int x, int v) {
		for (int i = x; i <= n; i += (i & -i)) {
			c[i] += v;
		}
	}
	il int query(int x) {
		int res = 0;
		for (int i = x; i > 0; i -= (i & -i)) {
			res += c[i];
		}
		return res;
	}
	il int query(int l, int r) {
		return l <= r ? query(r) - query(l - 1) : 0;
	}
} 
il int solve() {
	n = read();
	for (int i = 1; i <= n; i++) {
		a[i] = read();
	}
	for (int i = 1; i <= n; i++) {
		if (a[i] % 2 != i % 2) {
			printf("No\n");
			return 0;
		}
	}
	BIT::init();
	int cnt1 = 0;
	for (int i = 1; i <= n; i += 2) {
		cnt1 += BIT::query(a[i] + 1, n);
		BIT::update(a[i], 1);
	}
	BIT::init();
	int cnt2 = 0;
	for (int i = 2; i <= n; i += 2) {
		cnt2 += BIT::query(a[i] + 1, n);
		BIT::update(a[i], 1);
	}
	BIT::init();
	int cnt = 0;
	for (int i = 1; i <= n; i++) {
		cnt += BIT::query(a[i] + 1, n);
		BIT::update(a[i], 1);
	}
	if ((cnt1 + cnt2) * 3 == cnt) {
		printf("Yes\n");
	} else {
		printf("No\n");
	}
	
	return 0;
}
signed main() {
	int qq = read();
	while (qq--) {
		solve();
	}
	
	return 0;
}

T2 数据结构基础练习题

考虑把询问和修改离线下来。考虑把修改进行差分，拆成两个后缀的修改，分别为 \((l,x,t)\) 和 \((r+1,-x,t)\)，其中 \((pos,val,tim)\) 表示在时间 \(tim\) 时将 \([pos,n]\) 全部加上 \(val\)。

然后，考虑将询问和修改进行排序。位置为第一关键字，时间为第二关键字。

考虑枚举查询。当我们对于当前询问，把在这个询问之前的修改都类加上。然后对于当前询问统计答案即可。

放个核心代码。

sort(c + 1, c + 1 + cntc, cmp1);
sort(q + 1, q + 1 + cntq, cmp2); 
int j = 1;
for (int i = 1; i <= cntq; i++) {
    while (j <= cntc && (c[j].p < q[i].p || (c[j].p == q[i].p && c[j].t < q[i].t))) {
        update(c[j].t, m, c[j].x);
        j++;
    }
    ans[q[i].id] = kth(q[i].l, q[i].r, q[i].k);
}

然后这里的 update 和 kth 都暴力修改即可通过前两个包。

那然后就做完了呀。

直接考虑分块。

那么区间加就是简单的。考虑查询如何处理。对于每个块维护块内的数排序后的序列。询问时首先统计每个块内大于 \(x\) 的数，散块单独处理，整块直接二分。然后在外面在套一个二分即可求出第 \(k\) 大的数。

由于我们差分了，所以修改的那个数组应当开二倍。我本人因为没有开二倍调了五个小时。。

#include <bits/stdc++.h>
#define il inline

using namespace std;

namespace IO {
	const int bufsz = 1 << 20;
	char ibuf[bufsz], *p1 = ibuf, *p2 = ibuf;
	char obuf[bufsz], *p3 = obuf, stk[50];
	#define getchar() (p1 == p2 && (p2 = (p1 = ibuf) + fread(ibuf, 1, bufsz, stdin), p1 == p2) ? EOF : *p1++)
	#define flush() (fwrite(obuf, 1, p3 - obuf, stdout), p3 = obuf)
	#define putchar(ch) (p3 == obuf + bufsz && flush(), *p3++ = (ch))
	il int read() {
		int x = 0; char ch = getchar(); bool t = 0;
		while (ch < '0' || ch > '9') {t ^= ch == '-'; ch = getchar();}
		while (ch >= '0' && ch <= '9') {x = (x << 1) + (x << 3) + (ch ^ 48); ch = getchar();}
		return t ? -x : x;
	}
	il void write(int x, bool t = 1) {
		int top = 0;
		x < 0 ? putchar('-'), x = -x : 0; 
		do {stk[++top] = x % 10 | 48; x /= 10;} while(x);
		while(top) putchar(stk[top--]);
		t ? putchar('\n') : putchar(' ');
	}
	struct FL {~FL() {flush();}} fl;
	#undef getchar()
	#undef putchar()
	#undef flush()
}
using IO::read;
using IO::write;
const int N = 7e4 + 10, M = 300, maxn = 7e7;
int n, m;
struct nodec {
	int p, x, t;
} c[N * 2];
struct nodeq {
	int p, l, r, k, t, id;
} q[N];
il bool cmp1(nodec a, nodec b) {return a.p != b.p ? a.p < b.p : a.t < b.t;}
il bool cmp2(nodeq a, nodeq b) {return a.p != b.p ? a.p < b.p : a.t < b.t;}
int a[N];
int B, bn, st[M], ed[M], bel[N];
int add[M];
il void init() {
	B = 250, bn = 0;
	st[0] = ed[0] = -1;
	while (ed[bn] < m) {
		bn++;
		st[bn] = ed[bn - 1] + 1;
		ed[bn] = min(ed[bn - 1] + B, m);
		for (int i = st[bn]; i <= ed[bn]; i++) {
			bel[i] = bn;
		}
	}
}
int d[N];
il void upd(int x) {
	for (int i = st[bel[x]]; i <= ed[bel[x]]; i++) d[i] = a[i];
	sort(d + st[bel[x]], d + ed[bel[x]] + 1);
}
il void update(int l, int r, int x) {
	if (bel[l] == bel[r]) {
		for (int i = l; i <= r; i++) a[i] += x;
		upd(l);
		return;
	}
	for (int i = l; i <= ed[bel[l]]; i++) a[i] += x; upd(l);
	for (int i = st[bel[r]]; i <= r; i++) a[i] += x; upd(r);
	for (int i = bel[l] + 1; i <= bel[r] - 1; i++) {
		add[i] += x;
	}
}
il int query(int l, int r, int x) {
	if (bel[l] == bel[r]) {
		int res = 0;
		for (int i = l; i <= r; i++) res += (a[i] + add[bel[l]] <= x);
		return res;
	}
	int res = 0;
	for (int i = l; i <= ed[bel[l]]; i++) res += (a[i] + add[bel[l]] <= x);
	for (int i = st[bel[r]]; i <= r; i++) res += (a[i] + add[bel[r]] <= x);
	for (int i = bel[l] + 1; i <= bel[r] - 1; i++) {
		int L = st[i], R = ed[i], ans = 0;
		while (L <= R) {
			int mid = L + R >> 1;
			if (d[mid] + add[i] <= x) {
				ans = mid;
				L = mid + 1;
			} else {
				R = mid - 1;
			}
		}
		if (ans) res += ans - st[i] + 1;
	}
	return res;
}
il int kth(int l, int r, int k) {
	int L = -maxn, R = maxn, ans = 0;
	while (L <= R) {
		int mid = (L + R) >> 1;
		if (query(l, r, mid) >= k) {
			ans = mid;
			R = mid - 1;
		} else {
			L = mid + 1;
		}
	}
	return ans;
}
int ans[N];
int main() {
	n = read(), m = read();
	int cntc = 0, cntq = 0;
	for (int i = 1; i <= m; i++) {
		int op = read();
		if (op == 0) {
			int l = read(), r = read(), x = read();
			c[++cntc] = {l, x, i};
			c[++cntc] = {r + 1, -x, i};
		} else {
			int p = read(), l = read(), r = read(), k = read();
			q[++cntq] = {p, l, r, k, i};
			q[cntq].id = cntq;
		}
	}
	sort(c + 1, c + 1 + cntc, cmp1);
	sort(q + 1, q + 1 + cntq, cmp2); 
	init();
	int j = 1;
	for (int i = 1; i <= cntq; i++) {
		while (j <= cntc && (c[j].p < q[i].p || (c[j].p == q[i].p && c[j].t < q[i].t))) {
			update(c[j].t, m, c[j].x);
			j++;
		}
		ans[q[i].id] = kth(q[i].l, q[i].r, q[i].k);
	}
	for (int i = 1; i <= cntq; i++) {
		write(ans[i]);
	}
	
	return 0;
}

T3 制糊串

T4 牛仔

2025CSP-S模拟赛21

T1 T2 T3 T4
55 TLE 16 WA 0 WA 8 WA

排名：8/19；总分：79

T1 是 \(O(n\log^2 n)\) 做法，几近正解。余下的皆为骗分。

T1 kotori

这个赛时写的感觉几近正解。此处梳理我的思路。

首先考虑到所有启动的投票装置（下文称为特殊点）之间的简单路径后构成一个连通块，这个是显然的。那么，查询一个点的时候，由于他能走到一个特殊点，那么他就一定可以走到当前这个连通块内的所有点，以及他与其中一个特殊点之间的简单路径上的点。考虑树剖维护树中简单路径上的点的最小值，然后考虑在全局维护一个最小值用来维护连通块内点的最小值。时间复杂度 \(O(n \log^2n)\)。

然后就可以引申出正解。我们把第一个成为特殊点的点看作根，那么我们就只需维护根链上的最小值。而这个值有时不变的，所以一遍 dfs 处理即可。时间复杂度 \(O(n)\)。

#include <bits/stdc++.h>
#define il inline

using namespace std;

const int bufsz = 1 << 20;
char ibuf[bufsz], *p1 = ibuf, *p2 = ibuf;
#define getchar() (p1 == p2 && (p2 = (p1 = ibuf) + fread(ibuf, 1, bufsz, stdin), p1 == p2) ? EOF : *p1++)
il int read() {
	int x = 0; char ch = getchar(); bool t = 0;
	while (ch < '0' || ch > '9') {t ^= ch == '-'; ch = getchar();}
	while (ch >= '0' && ch <= '9') {x = (x << 1) + (x << 3) + (ch ^ 48); ch = getchar();}
	return t ? -x : x;
}
#undef getchar()
const int INF = 0x3f3f3f3f;
const int N = 1e6 + 10;
int n, qq;
vector<int> G[N];
int f[N];
void dfs(int x, int val, int fa) {
	f[x] = min(val, x);
	for (int y : G[x]) {
		if (y == fa) continue;
		dfs(y, f[x], x);
	}
}
int main() {
	n = read(), qq = read();
	for (int i = 1; i < n; i++) {
		int x = read(), y = read();
		G[x].push_back(y);
		G[y].push_back(x);
	}
	int lastans = 0;
	int lstx = 0;
	int mn = INF;
	while (qq--) {
		int op = read(), x = read();
		x = (x + lastans) % n + 1;
		if (op == 1) {
			if (!lstx) {
				lstx = x;
				dfs(x, INF, 0);
			}
			mn = min(mn, f[x]);
		} else {
			lastans = min(mn, f[x]);
			printf("%d\n", lastans);
		}
	}
	
	return 0;
}

T2 charlotte

这个换根挺屎的。神秘调了八九个小时。

设 \(siz_u\) 表示 \(u\) 子树中有棋子的点的个数，\(g_u\) 表示子树内所有棋子到 \(u\) 的距离和，\(f_u\) 表示一系列操作后能使 \(g_u\) 达到的最小值。直接说转移了：

\[\begin{array}{rl} siz_u & = & tag_u+\sum_{v \in son_u} siz_v\\ g_u & = & \sum_{v\in son_u} g_v+siz_v\\ f_u & = &\max_{v\in son_u}\{f_v+siz_v-(g_u-g_v-siz_v)\} \end{array} \]

然后就是如果 \(f_u\) 小于 0，应赋值为 \(g_u \bmod 2\)。具体看这儿吧，也懒得写了。答案就是 \(\min\{g_u/2\} ,(f_u=0)\)。

然后上个换根就行了。

这个换根还是很吃操作的。由于咱这个 \(f\) 的转移是取最大值，所以还得记录次大值。然后就是犯了个傻逼错误，在判全小于 0 的时候最开始是在转移的过程中判，就导致在换根时直接爆炸。（鸣谢 zhangxy__hp）实则只需判断最大值是否小于 0 即可。

这题貌似换根这个次大值还可以利用 set 来做。但是，你知道吧，STL 这东西我认为还是慎用。

#include <bits/stdc++.h>
#define il inline
#define int long long

using namespace std;

const int INF = 0x3f3f3f3f3f3f3f3f;
const int N = 1e6 + 10;
int n, tag[N];
char s[N];
vector<int> G[N];
int f[N], g[N], siz[N];
int f1[N], nxt[N], g1[N];
void dfs(int x, int fa) {
	siz[x] = tag[x];
	for (int y : G[x]) {
		if (y == fa) continue;
		dfs(y, x);
		siz[x] += siz[y];
		g[x] += g[y] + siz[y];
	}
	int flag = 1;
	for (int y : G[x]) {
		if (y == fa) continue;
		int num = f[y] + siz[y] - (g[x] - g[y] - siz[y]);
		flag &= (num < 0);
		f[x] = max(f[x], num);
	}
	if (flag) {
		f[x] = g[x] % 2;
	}
} 
int ss[N];
void dfs1(int x, int fa) {
	for (int y : G[x]) {
		if (y != fa) {
			g1[x] += g[y] + siz[y];
		} else {
			int sizy = siz[1] - siz[x];
			int gy = g1[y] - g[x] - siz[x];
			g1[x] += gy + sizy;
		}
	}
	ss[x] = G[x].size();
	for (int y : G[x]) {
		int num;
		if (y != fa) {
			num = f[y] + siz[y] - (g1[x] - g[y] - siz[y]);
		} else {
			int tmp = f[x] + siz[x] - (g1[y] - g[x] - siz[x]);
			int gy = g1[y] - g[x] - siz[x];
			int sizy = siz[1] - siz[x];
			int fy = (tmp != f1[y] ? f1[y] : nxt[y]);
			if (tmp != f1[y]) {
				fy = f1[y] + g1[y] - gy;
				if (fy < 0) fy = gy % 2;
			} else {
				if (ss[y] == 1) {
					fy = 0;
				} else {
					fy = nxt[y] + g1[y] - gy;
					if (fy < 0) fy = gy % 2;
				}
			}
			num = fy + sizy - (g1[x] - gy - sizy);
		}
		if (num > f1[x]) {
			nxt[x] = f1[x];
			f1[x] = num;
		} else if (num > nxt[x]) {
			nxt[x] = num;
		}
	}
	for (int y : G[x]) {
		if (y != fa) dfs1(y, x);
	}
}
signed main() {
	ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
	cin >> n >> s;
	for (int i = 1; i <= n; i++) {
		tag[i] = (s[i - 1] == '1');
	}
	for (int i = 1; i < n; i++) {
		int x, y;
		cin >> x >> y;
		G[x].push_back(y);
		G[y].push_back(x);
	}
	for (int i = 1; i <= n; i++) f1[i] = nxt[i] = -INF; 
	dfs(1, 0);
	dfs1(1, 0);
	for (int i = 1; i <= n; i++) {
		if (f1[i] < 0) f1[i] = g1[i] % 2;
	}
	int ans = INF;
	for (int i = 1; i <= n; i++) {
		if (f1[i] == 0) ans = min(ans, g1[i] / 2);
	}
	cout << (ans < INF ? ans : -1) << '\n';
	
	return 0;
}

T3 sagiri

T4 chtholly

2025CSP-S模拟赛22

T1 T2 T3 T4
60 TLE 0 TLE 0 TLE 0 TLE

排名：11/21；总分：60

T1 写了线段树并不断卡常，妄想 \(O(n \log n)\) 过 \(10^7\)。后三题就是没写出来。

T1 草莓列车（train）

这边我要展示我考试时不断卡常后的区间取 max、单点查询的线段树，非常帅气。

unsigned int mx[4 * N];
#define lc p << 1
#define rc p << 1 | 1
#define mid (l + r >> 1)
inline void build(int p, int l, int r) {
	if (l == r) return mx[p] = a[l], void();
	build(lc, l, mid), build(rc, mid + 1, r);
}
inline void update(int p, int l, int r, int x, int y, unsigned int v) {
	return (x <= l && r <= y ? mx[p] = max(mx[p], v): ((x <= mid ? update(lc, l, mid, x, y, v), 0 : 0),(mid < y ? update(rc, mid + 1, r, x, y, v), 0 : 0))), void();
}
inline unsigned int query(int p, int l, int r, int x, unsigned int tag) {
	return l == r ? max(mx[p], tag) : (x <= mid ? query(lc, l, mid, x, max(tag, mx[p])) : query(rc, mid + 1, r, x, max(tag, mx[p])));
}

直接考虑正解。

首先，我们关注到有一个东西叫做 ST 表，他可以实现 \(O(n\log n)\) 预处理，\(O(1)\) 查询区间极值。那我们现在考虑把他一整个反过来，让他实现 \(O(1)\) 区间修改，然后 \(O(n\log n)\) 处理出完整的 ST 表实现单点查询。直接上代码。

#include <bits/stdc++.h>

using namespace std;

const int N = 1e5 + 10;
int n, m, typ;
unsigned int a[N];
unsigned int xx, seed;
inline unsigned int getnum() {
	xx = (xx << 3) ^ xx;
	xx = ((xx >> 5) + seed) ^ xx;
	return xx;
}
int Log2[N];
unsigned int f[N][20];
int main() {
	ios::sync_with_stdio(0); cin.tie(0), cout.tie(0);
	cin >> n >> m >> typ;
	for (int i = 1; i <= n; i++) {
		cin >> a[i];
	}
	for (int i = 2; i <= n; i++) Log2[i] = Log2[i / 2] + 1;
	cin >> xx >> seed;
	int l, r, s;
	unsigned int v;
	for (int id = 1; id <= m; id++) {
		l = getnum() % n + 1, r = getnum() % n + 1;
		v = getnum();
		l > r ? (l ^= r ^= l ^= r) : 0;
		l = (typ == 1 ? 1 : l);
		//---- l r v
		s = Log2[r - l + 1];
		f[l][s] = max(f[l][s], v);
		f[r - (1 << s) + 1][s] = max(f[r - (1 << s) + 1][s], v);
	}
	for (int j = Log2[n]; j >= 1; j--) {
		for (int i = 1; i + (1 << j) - 1 <= n; i++) {
			f[i][j - 1] = max(f[i][j - 1], f[i][j]);
			f[i + (1 << j - 1)][j - 1] = max(f[i + (1 << j - 1)][j - 1], f[i][j]);
		}
	}
	for (int i = 1; i <= n; i++) {
		cout << max(a[i], f[i][0]) << ' ';
	}
	
	return 0;
}

T2 草莓路径（path）

CSP-S模拟赛 T2 出神秘线性基。。反正我是改不了一点。

T3 草莓城市（city）

CSP-S模拟赛 T3 出神秘 2-SAT。。反正我是改不了一点。

T4 草莓之歌（easy）

CSP-S模拟赛 T4 出神秘黑色 dp。。反正我是改不了一点。

这篇我认为写挺好的

首先，容易发现一个字符串能合法当且仅当第 \(i\) 个 A 在第 \(i\) 个 B 钱。那么一定是第 \([l,r]\) 个 A 去匹配第 \([l,r]\) 个 B。那么设 \(c_i\) 表示在第 \(i\) 个 A 前的 B 的个数，\(w(l,r)\) 表示将第 \([l+1,r]\) 个 A 和 B 尽心匹配的代价。则 \(w(l,r)=\sum_{i=l+1}^r \max(0,c_i-l)\)，相当于统计每个 A 交换的 B 的数量。

考虑 dp。设 \(f_{i,l}\) 表示当前划分出来了 \(l\) 个子序列，下一个子序列开头是第 \(i+1\) 个 A 的最小代价。转移即为 \(f_{i,l}+w(i,j) \rightarrow f_{j,l+1}\)。此时就解决了问题，时间复杂度 \(O(n^3)\)。

以上的部分都很好懂，后面就开了。我自己是费了很大精力理解的。

首先，\(w(i,j)\) 满足四边形不等式[1]，这个画个图就能理解。

然后，得出 \(f_{n,i}\) 是满足凸性的，而且是下凸包。题解给了个证明，反正我没看。UKE_Automation 给我讲的感性理解我也不是很理解。反正把这个结论记一下吧，后面能用了用。（满足四边形不等式的序列划分问题的答案凸性）

然后就使用 wqs 二分进行优化[2]，这个东西比较牛逼。反正然后 dp 式子就变为 \(f_j \leftarrow f_i+w(i,j)-mid\)。

进而考虑设 \(p_i\) 表示第一个满足 \(c_k \geq i\) 的 \(k\)，且 \(p_i=\max(p_i,i+1)\)，则 \(w(l,r)=\sum_{i=p_l}^r c_i-l\)。设 \(c_i\) 的前缀和为 \(s_i\)，则 \(w(l,r)=s_r-s_{p_l-1}-l\times(r-p_l+1)\)。

然后你发现这个 dp 是一个 1d1d 的转移，然后上斜率优化 dp [3]即可。

代码贴详细一点。

40pts：

memset(f, 0x3f, sizeof(f));
f[0][0] = 0;
for (int i = 0; i < n; i++) {
    for (int l = 0; l <= kk; l++) {
        for (int j = i + 1; j <= n; j++) {
            f[j][l + 1] = min(f[j][l + 1], f[i][l] + w(i, j));
        }
    }
}

60pts:

#include <bits/stdc++.h>
#define int long long
#define il inline

using namespace std;

const int INF = 0x3f3f3f3f3f3f3f3f;
const int N = 1e6 + 10;
int n, kk, a[2 * N];
char ss[2 * N];
int c[N], p[N], s[N];
int f[N], g[N]; 
il bool check(int mid) {
	for (int i = 1; i <= n; i++) {
		f[i] = g[i] = INF;
		for (int j = 0; j < i; j++) {
			int v = f[j] - mid;
			if (p[j] <= i) v += s[i] - s[p[j] - 1] - j * (i - p[j] + 1);
			if (v < f[i] || (v == f[i] && g[j] + 1 < g[i])) {
				f[i] = v, g[i] = g[j] + 1;
			}
		}
	}
	return g[n] <= kk;
}
signed main() {
	ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
	cin >> n >> kk >> ss;
	for (int i = 1; i <= 2 * n; i++) a[i] = (ss[i - 1] == 'A');
	int cnt = 0, tot = 0;
	for (int i = 1; i <= 2 * n; i++) {
		if (a[i] == 1) c[++tot] = cnt;
		else cnt++;
	}
	for (int i = 1; i <= n; i++) {
		p[i] = lower_bound(c + 1, c + 1 + n, i) - c;
		p[i] = max(p[i], i + 1);
	}
	for (int i = 1; i <= n; i++) {
		s[i] = s[i - 1] + c[i];
	}
	int L = -INF, R = 0, ans = 0;
	while (L <= R) {
		int mid = (L + R) / 2;
		if (check(mid)) {
			ans = mid;
			L = mid + 1;
		} else {
			R = mid - 1;
		}
	}
	check(ans);
	cout << f[n] + kk * ans << "\n";
	
	return 0;
}

100pts:

#include <bits/stdc++.h>
#define int long long
#define il inline

using namespace std;

const int INF = 0x3f3f3f3f3f3f3f3f;
const int N = 2e6 + 10;
int n, kk, a[N];
char ss[N];
int c[N], p[N], s[N];
int f[N], g[N]; 
int mid;
il int y(int j) {return -f[j] + s[p[j] - 1] - j * p[j] + j;}
il int k(int i) {return i;}
il int x(int j) {return -j;}
il int b(int i) {return -f[i] - mid + s[i];}
il double slope(int i, int j) {
	return 1.0 * (y(i) - y(j)) / (x(i) - x(j));
}
int q[N], head, tail;
vector<int> num[N];
il bool check(int mm) {
	mid = mm;
	for (int i = 1; i <= n; i++) f[i] = g[i] = INF;
	head = 1, tail = 0;
	for (int i = 1; i <= n; i++) {
		for (int j : num[i]) {
			while (head < tail && slope(q[tail - 1], q[tail]) > slope(q[tail], j)) tail--;
			q[++tail] = j;
		}
		while (head < tail && slope(q[head], q[head + 1]) < k(i)) head++;
		f[i] = -mid + s[i] - y(q[head]) + k(i) * x(q[head]);
		g[i] = g[q[head]] + 1;
	}
	return g[n] <= kk;
}
signed main() {
	ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
	cin >> n >> kk >> ss;
	for (int i = 1; i <= 2 * n; i++) a[i] = (ss[i - 1] == 'A');
	int cnt = 0, tot = 0;
	for (int i = 1; i <= 2 * n; i++) {
		if (a[i] == 1) c[++tot] = cnt;
		else cnt++;
	}
	for (int i = 0; i <= n; i++) {
		p[i] = lower_bound(c + 1, c + 1 + n, i) - c;
		p[i] = max(p[i], i + 1);
		num[p[i]].push_back(i);
	}
	for (int i = 1; i <= n; i++) {
		s[i] = s[i - 1] + c[i];
	}
	int L = -INF, R = 0, ans = 0;
	while (L <= R) {
		mid = (L + R) / 2;
		if (check(mid)) {
			ans = mid;
			L = mid + 1;
		} else {
			R = mid - 1;
		}
	}
	check(ans);
	cout << f[n] + kk * ans << "\n";
	
	return 0;
}

2025CSP-S模拟赛23

T1 T2 T3 T4
30 TLE 4 TLE 20 RE 15 TLE

排名：14/22；总分：69。

T1 第三个包打假了，少 10 分，T2 是大样例不明所以没过，T3 T4 均为部分分。

T1 origen

考虑拆位拆贡献。首先，我们将原式变为 \(\sum_{i=0}^n \sum_{j=i+1}^n(s_i\oplus s_j)^2\)，其中 \(s_i\) 是异或前缀和。然后拆位暴拆式子就行了。

\[\sum_{i=0}^n \sum_{j=i+1}^n(s_i\oplus s_j)^2 =\sum_{i=0}^n \sum_{j=i+1}^n(\sum_{k}(c_{i,k}\ne c_{j,k})\times2^k)^2 \]

然后随便维护一下就行了。

#include <bits/stdc++.h>
#define il inline
#define int long long

using namespace std;

const int bufsz = 1 << 20;
char ibuf[bufsz], *p1 = ibuf, *p2 = ibuf;
#define getchar() (p1 == p2 && (p2 = (p1 = ibuf) + fread(ibuf, 1, bufsz, stdin), p1 == p2) ? EOF : *p1++)
il int read() {
	int x = 0; char ch = getchar(); bool t = 0;
	while (ch < '0' || ch > '9') {t ^= ch == '-'; ch = getchar();}
	while (ch >= '0' && ch <= '9') {x = (x << 1) + (x << 3) + (ch ^ 48); ch = getchar();}
	return t ? -x : x;
}
const int MOD = 998244353;
const int N = 2e5 + 10, M = 20;
int n, a[N];
int s[N], c[M][2][M][2];
signed main() {
	n = read();
	for (int i = 1; i <= n; i++) {
		a[i] = read();
	}
	for (int i = 1; i <= n; i++) {
		s[i] = s[i - 1] ^ a[i];
	}
	for (int i = 0; i < M; i++)
		for (int j = 0; j < M; j++) c[i][0][j][0] = 1;
	int ans = 0;
	for (int i = 1; i <= n; i++) {
		for (int k1 = 0; k1 < M; k1++) {
			for (int k2 = 0; k2 < M; k2++) {
				int v1 = (s[i] >> k1) & 1, v2 = (s[i] >> k2) & 1;
				ans = (ans + c[k1][v1 ^ 1][k2][v2 ^ 1] * (1 << k1) % MOD * (1 << k2) % MOD) % MOD;
				c[k1][v1][k2][v2]++;
			}
		}
	}
	printf("%lld\n", ans);
	
	return 0;
}

T2 competiton

题解给了三种做法，这边选择了我认为比较好懂的一种做。

考虑正难则反。

首先假设一道题能被重复做多次，那么答案就是：

\[\sum_{i=1}^n(r_i-l_i+1)\times i\times (n-i+1) \]

即一个人能做的题目数量乘上一个人在多少区间中出现。

我们令 \(f_{i,j}\) 表示第 \(i\) 个人前面的最靠右的能做出题目 \(j\) 的人的编号。然后就可以发现 \(i\) 和 \(f_{i,j}\) 在做第 \(j\) 道题时会重复，多出的方案数即为 \(f_{i,j}\times(n-i+1)\)。

然后把第一维滚掉，用线段树动态维护 \(f\) 即可。

有一个细节点就是动态开店线段树常数太大了，所以要离散化处理。

#include <bits/stdc++.h>
#define int long long

using namespace std;

const int bufsz = 1 << 20;
char ibuf[bufsz], *p1 = ibuf, *p2 = ibuf;
#define getchar() (p1 == p2 && (p2 = (p1 = ibuf) + fread(ibuf, 1, bufsz, stdin), p1 == p2) ? EOF : *p1++)
inline int read() {
	int x = 0; char ch = getchar(); bool t = 0;
	while (ch < '0' || ch > '9') {t ^= ch == '-'; ch = getchar();}
	while (ch >= '0' && ch <= '9') {x = (x << 1) + (x << 3) + (ch ^ 48); ch = getchar();}
	return t ? -x : x;
}
const int MOD = 1e9 + 7;
const int N = 1e6 + 10;
int n;
int m, ll[N], rr[N];
inline int fpow(int a, int x) {
	int ans = 1;
	while (x) {
		if (x & 1) ans = ans * a % MOD;
		a = a * a % MOD;
		x >>= 1;
	}
	return ans;
}
inline int getny(int x) {
	return fpow(x, MOD - 2);
}
int lis[N << 1];
const int M = N << 5;
int s[M], lazy[M];
#define lc p << 1
#define rc p << 1 | 1
#define mid (l + r >> 1)
inline void pushdown(int p, int l, int r) {
	if (!lazy[p]) return;
	s[lc] = (lis[mid] - lis[l - 1]) % MOD * lazy[p] % MOD;
	s[rc] = (lis[r] - lis[mid]) % MOD * lazy[p] % MOD;
	lazy[lc] = lazy[p];
	lazy[rc] = lazy[p];
	lazy[p] = 0;
}
inline void update(int p, int l, int r, int x, int y, int v) {
	if (x == l && r == y) {
		s[p] = (lis[r] - lis[l - 1]) % MOD * v % MOD;
		lazy[p] = v;
		return;
	}
	pushdown(p, l, r);
	if (y <= mid) update(lc, l, mid, x, y, v);
	else if (x > mid) update(rc, mid + 1, r, x, y, v);
	else update(lc, l, mid, x, mid, v), update(rc, mid + 1, r, mid + 1, y, v);
	s[p] = (s[lc] + s[rc]) % MOD;
} 
inline int query(int p, int l, int r, int x, int y) {
	if (x == l && r == y) return s[p];
	pushdown(p, l, r);
	if (y <= mid) return query(lc, l, mid, x, y);
	else if (x > mid) return query(rc, mid + 1, r, x, y);
	else return (query(lc, l, mid, x, mid) + query(rc, mid + 1, r, mid + 1, y)) % MOD;
} 
signed main() {
	n = read(), m = read();
	int tt = 0;
	for (int i = 1; i <= n; i++) {
		ll[i] = read(), rr[i] = read();
		lis[++tt] = ll[i] - 1, lis[++tt] = rr[i];
	}
	sort(lis + 1, lis + 1 + tt);
	int len = unique(lis + 1, lis + 1 + tt) - lis - 1;
	for (int i = 1; i <= n; i++) {
		ll[i] = lower_bound(lis + 1, lis + 1 + len, ll[i] - 1) - lis;
		rr[i] = lower_bound(lis + 1, lis + 1 + len, rr[i]) - lis;
	}
	int ans = 0;
	for (int i = 1; i <= n; i++) {
		ans = (ans + (lis[rr[i]] - lis[ll[i]]) % MOD * i % MOD * (n - i + 1) % MOD) % MOD;
	} 
	int sum = 0;
	for (int i = 1; i <= n; i++) {
		sum = (sum + query(1, 1, len, ll[i] + 1, rr[i]) * (n - i + 1) % MOD) % MOD;
		update(1, 1, len, ll[i] + 1, rr[i], i);
	}
	ans = (ans - sum) % MOD * getny(n * (n + 1) % MOD * getny(2) % MOD) % MOD;
	ans = (ans + MOD) % MOD;
	printf("%lld\n", ans);
	
	return 0;
}

T3 tour

T4 abstract

2025CSP-S模拟赛24

T1 T2 T3 T4
20 WA 0 WA 20 TLE 0TLE

排名：14/22；总分：40

T1 傻逼构造，构造炸了。T2 不会，T3 暴力，T4 暴力挂了。

T1 构造

傻逼构造。

#include <bits/stdc++.h>
#define il inline

using namespace std;

il int read() {
	int x = 0; char ch = getchar(); bool t = 0;
	while (ch < '0' || ch > '9') {t ^= ch == '-'; ch = getchar();}
	while (ch >= '0' && ch <= '9') {x = (x << 1) + (x << 3) + (ch ^ 48); ch = getchar();}
	return t ? -x : x;
}
const int N = 2300, M = 50;
int n;
int a[M][M];
int main() {
	n = read();
	int cnt = 0, h = 40, w = 40;
	for (int i = 1; i <= h; i++)
		for (int j = 1; j <= w; j++) a[i][j] = 1;
	int k = 0;
	for (k = 0; k < 9 && cnt + 232 <= n; k++) {
		int i = k * 4;
		for (int j = 1; j <= w; j++) a[i + 1][j] = 1;
		for (int j = 1; j <= w; j++) a[i + 2][j] = 2;
		for (int j = 1; j <= w; j++) a[i + 3][j] = 3;
		for (int j = 1; j <= w; j++) a[i + 4][j] = 2;
		cnt += 232;
	}
	int l1 = k * 4 + 1, l2 = k * 4 + 2, l3 = k * 4 + 3;
	for (int i = 1; i <= w; i++) {
		a[l1][i] = 1;
	}
	if (n - cnt <= 3) {
		for (int i = 1; i <= w && cnt < n; i += 4) {
			a[h][i] = 1, a[h][i + 1] = 2, a[h][i + 2] = 3;
			cnt++;
		}
		for (int i = 1; i <= w && cnt < n; i += 4) {
			a[h][i + 3] = 2;
			cnt++;
		}
	} else {
		a[l2][1] = 2, a[l3][1] = 3;
		a[l2][2] = 2, a[l3][2] = 3;
		cnt += 3;
		int j;
		for (j = 3; j < w && cnt + 3 <= n; j++) {
			a[l2][j] = 2, a[l3][j] = 3;
			cnt += 3;
		}
		if (n - cnt >= 2 && j == w) {
			a[l2][j] = 2, a[l3][j] = 3;
			cnt += 2;
		}
		if (n - cnt >= 3 && j < w) {
			a[l2][j] = 2, a[l3][j] = 3;
			cnt += 3;
		}
	}
	if (n - cnt > 13 && k < 9) {
		l1 += 3, l2 += 3, l3 += 3;
		for (int i = 1; i <= w; i++) {
			a[l1][i] = 1;
		}
		a[l2][1] = 2, a[l3][1] = 3;
		a[l2][2] = 2, a[l3][2] = 3;
		cnt += 3;
		int j;
		for (j = 3; j < w && cnt + 3 <= n; j++) {
			a[l2][j] = 2, a[l3][j] = 3;
			cnt += 3;
		}
		if (n - cnt >= 2 && j == w) {
			a[l2][j] = 2, a[l3][j] = 3;
			cnt += 2;
		}
		if (n - cnt >= 3 && j < w) {
			a[l2][j] = 2, a[l3][j] = 3;
			cnt += 3;
		}
	}
	for (int i = 1; i < w && cnt < n; i += 3) {
		for (int i = 1; i <= w && cnt < n; i += 4) {
			a[h][i] = 1, a[h][i + 1] = 2, a[h][i + 2] = 3;
			cnt++;
		}
		for (int i = 1; i <= w && cnt < n; i += 4) {
			a[h][i + 3] = 2;
			cnt++;
		}
	} 
	printf("%d %d\n", h, w);
	for (int i = 1; i <= h; i++) {
		for (int j = 1; j <= w; j++) {
			if (a[i][j] == 1) printf("r");
			if (a[i][j] == 2) printf("y");
			if (a[i][j] == 3) printf("x");
		}
		printf("\n");
	}
	
	return 0;
}

T2 游戏

傻逼二极管题（全场不是 100 就是 0）。

二分答案 \(mid\)，我们只关注学生能否使得被抓人数 \(\le mid\)。

那么，人数 \(\le mid\) 的实验室就无关紧要了，我们只考虑人数大于 \(mid\) 的实验室。设同学有 \(p_i\) 的概率进入这个实验室，那么老师如果进入这个实验室抓到人的期望就是 \((1-p_i)\times a_i\)。所以我们要求对于任意这样的 \(a_i\)，都有 \((1-p_i)\times a_i\le mid\)，据此求出 \(p_i\) 的下界，判断全加起来到不到 \(1\) 即可。

没了。

#include <bits/stdc++.h>
#define il inline

using namespace std;

il int read() {
	int x = 0; char ch = getchar(); bool t = 0;
	while (ch < '0' || ch > '9') {t ^= ch == '-'; ch = getchar();}
	while (ch >= '0' && ch <= '9') {x = (x << 1) + (x << 3) + (ch ^ 48); ch = getchar();}
	return t ? -x : x;
}
const double eps = 1e-12;
const int N = 30 + 10;
int n, a[N];
il bool check(double mid) {
	double p = 0;
	for (int i = 1; i <= n; i++) {
		if (a[i] > mid) {
			p += 1.0 - mid * 1.0 / a[i];
		}
	}
	return p >= 1;
}
int main() {
	n = read();
	int mx = 0;
	for (int i = 1; i <= n; i++) {
		a[i] = read();
		mx = max(mx, a[i]);
	}
	double L = 0, R = mx, ans = 0;
	while (L + eps < R) {
		double mid = (L + R) / 2.0;
		if (check(mid)) {
			ans = mid;
			L = mid;
		} else {
			R = mid;
		}
	}
	printf("%.12lf\n", ans);
	
	return 0;
}

T3 数数

T4 滈葕

出题人也是人才。

据 UKE_Automation 所说（本题英文名为 dopetobly）：

这个题目标题和英文令人捉摸不透，考虑进行搜索，然后发现汉字标题和英文都不是一个有意义的词，所以需要进行一些脑洞。考虑谐音，发现这两个字都是多音字，也很难看出其真正含义。真正的突破口在于这个不存在的英文单词，注意到将字母重排后可以得到单词 bloodtype，即血型，并且正好可以和前面的汉字对应，所以我们确定了题目标题想表达的含义是血型。

这是题解给的一段资料：

ABO 血型系统是血型系统的一种，把血液分为 A,B,AB,O 四种血型。血液由红细胞和血清等组成，红细胞表面 有凝集原，血清内有凝集素。根据红细胞表面有无凝集原 A 和 B 来划分血液类型。红细胞上只有凝集原 A 的 为 A 型血，其血清中有抗 B 凝集素；红细胞上只有凝集原 B 的为 B 型血，其血清中有抗 A 凝集素；红细胞上 两种凝集原都有的为 AB 型血，其血清中无凝集素；红细胞上两种凝集原皆无者为 O 型，其血清中两种凝集素 皆有。有凝集原 A 的红细胞可被抗 A 凝集素凝集；有凝集原 B 的红细胞可被抗 B 凝集素凝集。配血试验是两 个人分别提供红细胞和血清并将其混合，观察是否有凝集反应。

然后，我们发现，A,B,C,D 的点权可以分别代表 A,B,AB,O 型血，然后一条边代表一次配血试验，边权表示是否发生凝集。

考虑将一种血型拆成“X 凝集原 + 抗 Y 凝集素”的形式，由于同种凝集原和同种凝集素不能同时出现，那么我们就把这道题转化成了一个 2-SAT 问题（小编觉得这种做法非常巧妙，于是去学习了 2-SAT）。对每一个点设置 \(a_i,b_i\)，分别表示是否含有 A/B 凝集原。对每一条边根据是否发生凝集列出与或式，然后跑 2-SAT 就行了。具体的：

显然 A 凝集原和抗 A 凝集素相遇的条件是 \(a_x \wedge \neg a_y\)，B 种同理。那么，每次配血试验写下来就是：\(w=(a \wedge \neg a_y) \vee (b_x \wedge \neg b_y)\)。

若 \(w=0\)，则有 \(\neg\left(a_{x} \wedge \neg a_{y}\right) \wedge \neg\left(b_{x} \wedge \neg b_{y}\right)=\left(\neg a_{x} \vee a_{y}\right) \wedge\left(\neg b_{x} \vee b_{y}\right)\)。

若 \(w=1\)，则有 $\left(a_{x} \wedge \neg a_{y}\right) \vee\left(b_{x} \wedge \neg b_{y}\right)=\left(a_{x} \vee b_{x}\right) \wedge\left(a_{x} \vee \neg b_{y}\right) \wedge\left(\neg a_{y} \vee b_{x}\right) \wedge\left(\neg a_{y} \vee \neg b_{y}\right) $。

#include <bits/stdc++.h>
#define il inline

using namespace std;

il int read() {
	int x = 0; char ch = getchar(); bool t = 0;
	while (ch < '0' || ch > '9') {t ^= ch == '-'; ch = getchar();}
	while (ch >= '0' && ch <= '9') {x = (x << 1) + (x << 3) + (ch ^ 48); ch = getchar();}
	return t ? -x : x;
}
const int N = 2e6 + 10;
int n, m;
vector<int> G[N];
il int P(int x, int a) {return a ? x + n : x;}
il int V(int x, int a) {return a ? x : x + 2 * n;}
il void add(int x, int a, int y, int b) {
	G[V(x, a ^ 1)].push_back(V(y, b));
	G[V(y, b ^ 1)].push_back(V(x, a));
}
int dfn[N], low[N], tot, inst[N], st[N], head, scc[N], cnt;
il void tarjan(int x) {
	dfn[x] = low[x] = ++tot;
	st[++head] = x;
	inst[x] = 1;
	for (int y : G[x]) {
		if (!dfn[y]) {
			tarjan(y);
			low[x] = min(low[x], low[y]);
		} else if (inst[y]) {
			low[x] = min(low[x], dfn[y]);
		}
	}
	if (dfn[x] == low[x]) {
		cnt++;
		while (true) {
			int y = st[head--];
			inst[y] = 0;
			scc[y] = cnt;
			if (x == y) break;
		} 
	}
}
int main() {
	n = read(), m = read();
	for (int i = 1; i <= m; i++) {
		int x = read(), y = read(), w = read();
		if (w == 0) {
			add(P(x, 0), 0, P(y, 0), 1);
			add(P(x, 1), 0, P(y, 1), 1);
		} else {
			add(P(x, 0), 1, P(x, 1), 1);
			add(P(x, 0), 1, P(y, 1), 0);
			add(P(y, 0), 0, P(x, 1), 1);
			add(P(y, 0), 0, P(y, 1), 0);
		}
	}
	for (int i = 1; i <= 4 * n; i++) {
		if (!dfn[i]) tarjan(i);
	}
	for (int i = 1; i <= n * 2; i++) {
		if (scc[i] == scc[i + n * 2]) {
			printf("NO\n");
			return 0;
		}
	}
	printf("YES\n");
	for (int i = 1; i <= n; i++) {
		int aa = (scc[i + 2 * n] < scc[i]);
		int bb = (scc[i + n + 2 * n] < scc[i + n]);
		if (aa && !bb) printf("B");
		if (!aa && bb) printf("A");
		if (aa && bb) printf("D");
		if (!aa && !bb) printf("C");
	}
	
	return 0;
}

2025CSP-S模拟赛25

T1 T2 T3 T4
100 AC 100 AC 20 TLE 10 PE

排名：4/23；总分：230

比较有实力。T1 构造直接切，T2 dfs + 剪枝跑过了，T3 T4 均为部分分。

这场人均 200+，比较简单，没挂分。

一句话：花卉市场送福利。

T1 花昌蒲

观察大样例找规律，是简单的构造。

#include <bits/stdc++.h>

using namespace std;

int n, m;
pair<int, int> ans[10000];
int tot;
int main() {
	scanf("%d%d", &n, &m);
	if (m == 0) {
		if (n == 3) {
			printf("0\n");
			return 0;
		}
		printf("%d\n", n + 1);
		for (int i = 1; i <= n; i++) {
			printf("%d %d\n", i, n + 1);
		}
		return 0;
	}
	if (n - m < 2) {
		printf("0\n");
		return 0;
	}
	int cnt1 = m + 2, cnt2 = m;
	int id = 1;
	for (int i = 1; i < m; i++) {
		ans[++tot] = {id, id + 1};
		id++;
	}
	for (int i = 1; i <= m; i++) {
		ans[++tot] = {i, id + 1};
		id++;
	}
	ans[++tot] = {1, ++id};
	ans[++tot] = {m, ++id};
	if (cnt1 == n && cnt2 == m) {
		printf("%d\n", tot + 1);
		for (int i = 1; i <= tot; i++) {
			printf("%d %d\n", ans[i].first, ans[i].second);
		}
		return 0;
	}
	if (n - cnt1 == 1) {
		printf("0\n");
		return 0;
	}
	int lst = id;
	for (int i = 1; i <= n - cnt1 + 1; i++) {
		ans[++tot] = {lst, ++id};
	}
	printf("%d\n", tot + 1);
	for (int i = 1; i <= tot; i++) {
		printf("%d %d\n", ans[i].first, ans[i].second);
	}
	
	
	return 0;
}

T2 百日草

dfs + 剪枝直接跑过，这就是大常数选手的蜕变。

#include <bits/stdc++.h>
#define il inline
#define int long long

using namespace std;

const int bufsz = 1 << 20;
char ibuf[bufsz], *p1 = ibuf, *p2 = ibuf;
#define getchar()  (p1 == p2 && (p2 = (p1 = ibuf) + fread(ibuf, 1, bufsz, stdin), p1 == p2) ? EOF : *p1++)
il int read() {
	int x = 0; char ch = getchar(); bool t = 0;
	while (ch < '0' || ch > '9') {t ^= ch == '-'; ch = getchar();}
	while (ch >= '0' && ch <= '9') {x = (x << 1) + (x << 3) + (ch ^ 48); ch = getchar();}
	return t ? -x : x;
}
const int INF = 0x3f3f3f3f3f3f3f3f;
const int N = 3e5 + 10;
int n, m;
struct edge {
	int y, w;
};
vector<edge> G[N];
int f[N];
int ans;
il void dfs(int x, int t, int v) {
	if (v >= ans || v >= f[x] || t >= n) return;
	if (x == n) {
		ans = min(ans, v);
		return;
	}
	f[x] = v;
	for (edge i : G[x]) {
		dfs(i.y, t + 1, max(v, i.w * (t + 1)));
	}
}
signed main() {
	n = read(), m = read();
	for (int i = 1; i <= m; i++) {
		int x = read(), y = read(), w = read();
		G[x].push_back({y, w});
	}
	for (int i = 1; i <= n; i++) f[i] = INF;
	ans = INF;
	dfs(1, 0, 0);
	printf("%lld\n", ans);
	
	return 0;
}

T3 紫丁香

T4 麒麟草

2025CSP-S模拟赛26

T1 T2 T3 T4
100 AC - 0 TLE 0 RE

排名：10/24；总分：100

T1 集合

双指针扫一遍，权值线段树维护区间最大子段和即可。

#include <bits/stdc++.h>
#define il inline
#define int long long

using namespace std;

const int bufsz = 1 << 20;
char ibuf[bufsz], *p1 = ibuf, *p2 = ibuf;
#define getchar() (p1 == p2 && (p2 = (p1 = ibuf) + fread(ibuf, 1, bufsz, stdin), p1 == p2) ? EOF : *p1++)
il int read() {
	int x = 0; char ch = getchar(); bool t = 0;
	while (ch < '0' || ch > '9') {t ^= ch == '-'; ch = getchar();}
	while (ch >= '0' && ch <= '9') {x = (x << 1) + (x << 3) + (ch ^ 48); ch = getchar();}
	return t ? -x : x;
}
const int INF = 0x3f3f3f3f3f3f3f3f;
const int N = 2e5 + 10;
int n, kk, a[N];
struct node {
	int l, r, mx, s, lmx, rmx, val;
} tree[4 * N];
#define lc p << 1
#define rc p << 1 |1
il void build(int p, int l, int r) {
	tree[p].l = l, tree[p].r = r;
	if (l == r) return;
	int mid = l + r >> 1;
	build(lc, l, mid), build(rc, mid + 1, r);
}
il void pushup(int p) {
	tree[p].s = tree[lc].s + tree[rc].s;
	tree[p].lmx = max(tree[lc].lmx, (tree[lc].s == tree[lc].r - tree[lc].l + 1 ? tree[lc].s + tree[rc].lmx : -INF));
	tree[p].rmx = max(tree[rc].rmx, (tree[rc].s == tree[rc].r - tree[rc].l + 1 ? tree[rc].s + tree[lc].rmx : -INF));
	tree[p].mx = max(tree[lc].rmx + tree[rc].lmx, max(tree[lc].mx, tree[rc].mx));
}
il void update(int p, int x, int v) {
	if (tree[p].l == tree[p].r) {
		tree[p].val += v;
		tree[p].s = tree[p].mx = tree[p].lmx = tree[p].rmx = (tree[p].val >= 1);
		return;
	}
	int mid = tree[p].l + tree[p].r >> 1;
	if (x <= mid) update(lc, x, v);
	else update(rc, x, v);
	pushup(p);
}
signed main() {
	n = read(), kk = read();
	for (int i = 1; i <= n; i++) a[i] = read();
	build(1, 1, n);
	int l = 1, r = 1, lstl = 0;
	int cnt = 0;
	for (; l <= n; l++) {
		for (; r <= n && tree[1].mx <= kk; r++) {
			update(1, a[r], 1);
		}
		if (tree[1].mx > kk) {
			cnt += (l - lstl) * (n - (r - 1) + 1);
			lstl = l;
		}
		update(1, a[l], -1);
	}
	int ans = n * (n + 1) / 2 - cnt;
	printf("%lld\n", ans);
	
	return 0;
}

T2 差后队列

此题被题解称为签到题，确实不难。但是由于打完比赛当天脑子不好，改了一下午一晚上没看懂，第二天早上随意做 50 min 切掉。

这篇写的挺好，看吧。

#include <bits/stdc++.h>
#define il inline
#define int long long

using namespace std;

const int bufsz = 1 << 20;
char ibuf[bufsz], *p1 = ibuf, *p2 = ibuf;
#define getchar() (p1 == p2 && (p2 = (p1 = ibuf) + fread(ibuf, 1, bufsz, stdin), p1 == p2) ? EOF : *p1++)
il int read() {
	int x = 0; char ch = getchar(); bool t = 0;
	while (ch < '0' || ch > '9') {t ^= ch == '-'; ch = getchar();}
	while (ch >= '0' && ch <= '9') {x = (x << 1) + (x << 3) + (ch ^ 48); ch = getchar();}
	return t ? -x : x;
}
const int INF = 0x3f3f3f3f3f3f3f3f;
const int MOD = 998244353;
const int N = 1e6 + 10;
int n;
il int fpow(int a, int x) {
	a %= MOD;
	int ans = 1;
	while (x) {
		if (x & 1) ans = ans * a % MOD;
		a = a * a % MOD;
		x >>= 1;
	}
	return ans;
}
il int ny(int x) {
	return fpow(x, MOD - 2);
}
int op[N], a[N], t[N], c[N];
int ans[N];
vector<int> num[N];
signed main() {
	n = read();
	int sum = 0, cnt = 0, mx = 0, mxid = 0;
	for (int i = 1; i <= n; i++) {
		op[i] = read();
		if (op[i] == 0) {
			a[i] = read();
			sum = (sum + a[i]) % MOD;
			cnt++;
			if (a[i] > mx) {
				t[mxid] = i; 
				num[i].push_back(mxid);
				mx = a[i], mxid = i;
			} else {
				t[i] = i;
				num[i].push_back(i);
			}
		} else {
			if (cnt == 1) {
				ans[i] = mx;
				ans[mxid] = i;
				mx = mxid = sum = cnt = 0;
			} else {
				ans[i] = (sum - mx) % MOD  * ny(cnt - 1) % MOD;
				sum = (sum - ans[i]) % MOD;
				c[i] = cnt;
				cnt--;
			}
		}
	}
	int val = 0;
	for (int i = n; i >= 1; i--) {
		if (op[i] == 1) {
			val = (i * ny(c[i] - 1) % MOD + (1 - ny(c[i] - 1)) % MOD * val) % MOD;
		}
		for (int j : num[i]) ans[j] = val;
	}
	for (int i = 1; i <= n; i++) {
		printf("%lld ", (ans[i] + MOD) % MOD);
	}
	
	return 0;
}

T3 蛋糕

T4 字符替换

2025CSP-S模拟赛28

T1 T2 T3 T4
100 AC 25 TLE 20 TLE 15TLE

排名：1/15；总分：160

T1 用了 40 分钟切掉，后三题均为部分分。只写了最基础的一档，头部的人不在，别人又大挂分，于是拿下 rk1。

T1 路径

原图是 DAG，那拓扑排一下然后简单 dp 统计到每个点的路径上能经过的特殊点的最大值是多少。

#include <bits/stdc++.h>
#define il inline

using namespace std;

const int bufsz = 1 << 20;
char ibuf[bufsz], *p1 = ibuf, *p2 = ibuf;
#define getchar() (p1 == p2 && (p2 = (p1 = ibuf) + fread(ibuf, 1, bufsz, stdin), p1 == p2) ? EOF : *p1++)
il int read() {
	int x = 0; char ch = getchar(); bool t = 0;
	while (ch < '0' || ch > '9') {t ^= ch == '-'; ch = getchar();}
	while (ch >= '0' && ch <= '9') {x = (x << 1) + (x << 3) + (ch ^ 48); ch = getchar();}
	return t ? -x : x;
}
const int N = 1e6 + 10;
int n, m, kk;
int tag[N], rudu[N];
vector<int> G[N];
queue<int> q;
int f[N];
il int solve() {
	n = read(), m = read();
	for (int i = 1; i <= n; i++) {
		G[i].clear();
		tag[i] = rudu[i] = f[i] = 0;
	}
	for (int i = 1; i <= m; i++) {
		int x = read(), y = read();
		G[x].push_back(y);
		rudu[y]++;
	}
	kk = read();
	for (int i = 1; i <= kk; i++) {
		int x = read();
		tag[x] = 1;
	}
	while (!q.empty()) q.pop();
	for (int i = 1; i <= n; i++) {
		if (rudu[i] == 0) q.push(i);
	}
	while (!q.empty()) {
		int x = q.front(); q.pop();
		f[x] += tag[x];
		for (int y : G[x]) {
			f[y] = max(f[y], f[x]);
			rudu[y]--;
			if (rudu[y] == 0) q.push(y);
		}
	}
	int ans = 0;
	for (int i = 1; i <= n; i++) {
		ans |= (f[i] == kk);
	}
	if (ans) {
		printf("Yes\n");
	} else {
		printf("No\n");
	}
	
	return 0;
}
int main() {
	int qq = read();
	while (qq--) {
		solve();
	}
	
	return 0;
}

T2 异或

个人认为本题思路比较神仙。

首先将原序列转化成差分序列，那么区间修改就被转化为单点修改。那么一次修改操作即为单点修改或双点修改。下面提到的操作都基于差分序列。

那么我们的目标在于把整个序列全部变为 0。考虑将 \(n\) 个数抽象成 \(n\) 个点，将一次修改抽象成一条边，那么一组合法的方案就由若干个连通块组成。如果设每个连通块的大小为 \(x\)，则连通块的大小为 \(x-1\)（全是双点修改）或 \(x\)（存在一个单点修改）。

然后，有一个结论叫做：当且仅当连通块内的数异或和为 \(0\) 时边数为 \(x-1\)。附上题解给的证明：

必要性：显然每次操作都是双点修改，那么整个连通块内的数异或和不会变化，而最终要变为 \(0\)，那么 开始时必须是 \(0\)。

充分性：考虑一条串起连通块内的所有数的链。每次将链头通过异或自己的方式删掉，下一个数受到影 响后成为新的链头。经历 \(x-1\) 次操作后，最后一个数肯定是 \(0\)，无需再操作。

所以说，如果一个子序列内的数异或和为 \(0\) 则将该子序列清零的最小操作次数为子序列大小减一，否则即为该子序列大小。

然后状压即可，转移枚举补集的子集刷表即可。

#include <bits/stdc++.h>
#define int long long
#define il inline

using namespace std;

const int bufsz = 1 << 20;
char ibuf[bufsz], *p1 = ibuf, *p2 = ibuf;
#define getchar() (p1 == p2 && (p2 = (p1 = ibuf) + fread(ibuf, 1, bufsz, stdin), p1 == p2) ? EOF : *p1++)
il int read() {
	int x = 0; char ch = getchar(); bool t = 0;
	while (ch < '0' || ch > '9') {t ^= ch == '-'; ch = getchar();}
	while (ch >= '0' && ch <= '9') {x = (x << 1) + (x << 3) + (ch ^ 48); ch = getchar();}
	return t ? -x : x;
}
const int INF = 0x3f3f3f3f3f3f3f3f;
const int N = 20, M = 140000;
int n, a[N], ms, d[N];
int f[M], sum[M], cnt[M];
signed main() {
	n = read();
	for (int i = 1; i <= n; i++) a[i] = read();
	for (int i = 1; i <= n; i++) {
		d[i] = a[i] ^ a[i - 1];
	}
	ms = (1 << n) - 1;
	for (int st = 0; st <= ms; st++) {
		for (int i = 1; i <= n; i++) {
			if ((st >> i - 1) & 1) {
				sum[st] ^= d[i];
				cnt[st]++;
			}
		}
	}
	for (int i = 0; i <= ms; i++) f[i] = INF;
	f[0] = 0;
	for (int st = 0; st < ms; st++) {
		int s = ms - st;
		for (int ss = s; ss > 0; ss = (ss - 1) & s) {
			f[st | ss] = min(f[st | ss], f[st] + (sum[ss] ? cnt[ss] : cnt[ss] - 1));
		}
	}
	printf("%lld\n", f[ms]);
	
	return 0;
}

T3 距离

T4 花之舞

  1. 如果对于二元函数 \(w(i,j)\) 满足对于 \(\forall l_1\le l_2 \le r_1 \le r_2\) 都有 \(w(l_1,r_1)+w(l_2,r_2)\le w(l_1,r_2)+w(l_2,r_1)\)，则称 \(w(i,j)\) 满足四边形不等式。 ↩︎

  2. 自己去百度啊。就是二分一个斜率，然后非常牛逼进行一堆操作优化了复杂度并降维。 ↩︎

  3. 推销：斜率优化DP - Zctf1088 - 博客园 (cnblogs.com)。 ↩︎

posted @ 2025-10-19 20:26  Zctf1088  阅读(13)  评论(0)    收藏  举报