点分治

概念

点分治是树分治的一种，主要用于解决树上路径问题。

实现

贴上例题：

P3806 【模板】点分治 1

给定一棵有 \(n\) 个点的树，询问树上距离为 \(k\) 的点对是否存在。

考虑对于树上的所有路径，可以分为两类：

经过当前根节点的。
不经过当前根节点的。

对于第一种情况，我们直接求解。对于第二种情况，他们一定在根节点的某个子树中，考虑递归求解。

但是，如果我们随机找一个点作为根节点来求解，显然是不一定会是最优的，甚至可以被卡成 \(O(n)\)。所以，我们考虑以树的重心作为初始根节点，让他深度平衡，就可以保证时间复杂度为 \(O(\log n)\)。

总结一下点分治的基本步骤：

找出当前子树的重心。
根据题意对于当前子树进行统计答案。
分治各个子树，然后重复这三步。

这就是点分治的基本思想。

代码：

#include <bits/stdc++.h>
#define il inline

using namespace std;

il int read() {
	int x = 0; char ch = getchar(); bool t = 0;
	while (ch < '0' || ch > '9') {t ^= ch == '-'; ch = getchar();}
	while (ch >= '0' && ch <= '9') {x = (x << 1) + (x << 3) + (ch ^ 48); ch = getchar();}
	return t ? -x : x;
}
const int N = 1e4 + 10, M = 1e7 + 10;
int n, m, a[N];
struct edge {
	int y, w;
};
vector<edge> G[N];
int cen;
int siz[N], sum;
int fl[N];
il void getcen(int x, int fa) {
	siz[x] = 1;
	int mx = 0;
	for (edge i : G[x]) {
		if (fl[i.y] || i.y == fa) continue;
		getcen(i.y, x);
		siz[x] += siz[i.y];
		mx = max(mx, siz[i.y]);
	}
	mx = max(mx, sum - siz[x]);
	if (mx <= sum / 2) cen = x;
}
int dis[N], d[N], cnt;
il void getdis(int x, int fa) {
	d[++cnt] = dis[x];
	for (edge i : G[x]) {
		if (fl[i.y] || i.y == fa) continue;
		dis[i.y] = dis[x] + i.w;
		getdis(i.y, x);
	}
}
bitset<M> vis;
int p[N], tot;
int ans[N];
il void dfs(int x, int fa) {
	fl[x] = 1;
	vis[0] = 1;
	tot = 0;
	for (edge i : G[x]) {
		if (fl[i.y] || i.y == fa) continue;
		cnt = 0;
		dis[i.y] = i.w;
		getdis(i.y, x);
		for (int j = 1; j <= cnt; j++) {
			for (int k = 1; k <= m; k++) {
				if (a[k] >= d[j]) {
					ans[k] |= vis[a[k] - d[j]];
				}
			}
		}
		for (int j = 1; j <= cnt; j++) {
			if (d[j] >= M) continue;
			p[++tot] = d[j];
			vis[d[j]] = 1;
		}
	}
	for (int i = 1; i <= tot; i++) {
		vis[p[i]] = 0;
	}
	for (edge i : G[x]) {
		if (fl[i.y] || i.y == fa) continue;
		sum = siz[i.y];
		getcen(i.y, 0);
		dfs(cen, 0);
	}
}
int main() {
	n = read(), m = read();
	for (int i = 1; i < n; i++) {
		int x = read(), y = read(), w = read();
		G[x].push_back({y, w});
		G[y].push_back({x, w});
	}
	for (int i = 1; i <= m; i++) {
		a[i] = read();
	}
	sum = n;
	getcen(1, 0);
	dfs(cen, 0);
	for (int i = 1; i <= m; i++) {
		if (ans[i]) {
			printf("AYE\n");
		} else {
			printf("NAY\n");
		}
	}
	
	return 0;
}

动态点分治

动态点分治，就是基于点分治加以变化，构建出一棵重构树，就叫做点分树。

基本概念

具体的，就是将这一层的重心与上一层额重心连边，建出一棵重构树，就叫做点分树。

有什么用呢？点分治可以查询树上路径相关问题，但是涉及修改和多次询问，点分治就显得乏力。于是，我们利用点分治的思想建树。比如下图这棵树：

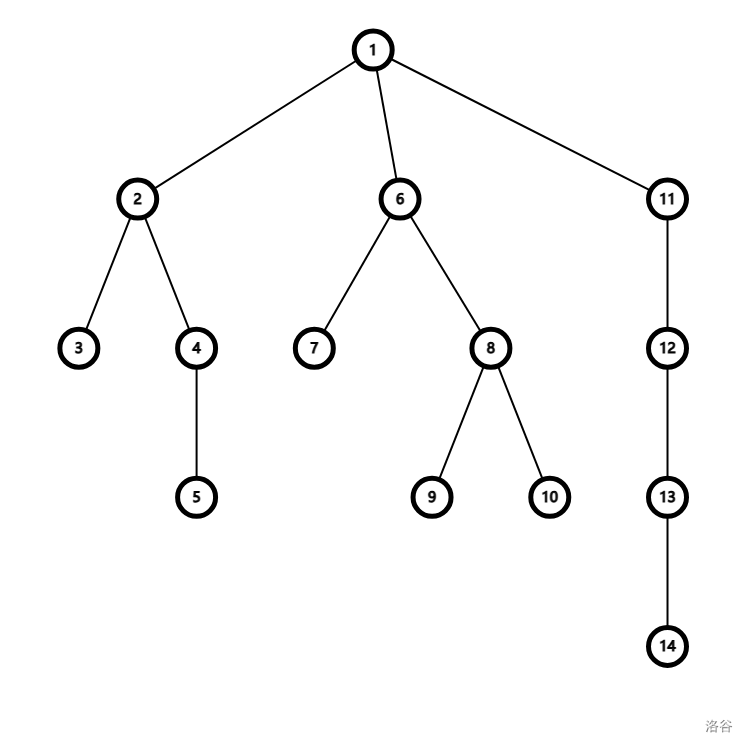
构造点分树为：

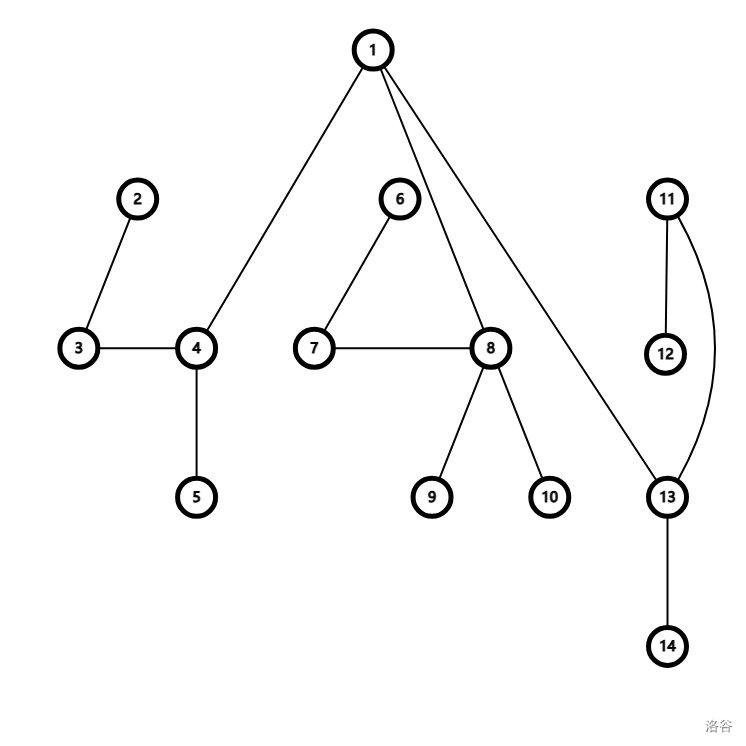
然后点分树没啥有用的。但是他有一个特别牛逼的性质：对于两点 \(x,y\)，他们在点分树上的 LCA，必然在原树 \(x \rightarrow y\) 的路径上。还有一个性质就是由于每次都连的是原树上的重心，所以树高不会超过 \(\log n\)。

我们就利用这些性质做题。

例题

P6329 【模板】点分树 | 震波

有一棵树，每个点有点权 \(a_i\)，每次进行两种操作中的一种：

给出 \(x,y\)，将 \(a_x\) 改为 \(y\)。

给出 \(x,k\)，求 \(\sum_{dis(x,y) \le k} a_y\)。

考虑利用点分树。

重点在于操作二。此时 \(x\) 是定点，\(y\) 在变化。考虑枚举 \(x,y\) 在点分树上所有可能的 LCA，记为 \(l\)。那么可得 \(dis(x,y)=dis(x,l)+dis(l,y)\)。注意，此处的 \(dis\) 是原树上的。

那么要求的答案就转化为：

\[\sum_{dis(x,l)+dis(l,y) \le k \land lca(x,y)=l} a_y \]

移项得：

\[\sum_{dis(l,y)\le k-dis(x,l) \land lca(x,y)=l} a_y \]

那么现在 \(l,x,k\) 都是定的，也就是求合法的 \(y\)。

首先考虑满足 \(lca(x,y)=l\)。显然是 \(l\) 的子树除去 \(l\) 在 \(x\) 方向上的儿子 \(p\) 的子树。

那么现在要求的就是在这部分子树中满足 \(dis(l,y) \le k-dis(l,x)\) 的 \(y\) 的权值和。那其实答案就是 \(l\) 的子树内距离 \(\le k-dis(x,l)\) 的点的权值和减去 \(p\) 的子树内到 \(l\) 的距离 \(\le k-dis(x,l)\) 的点的权值和。

那现在就可以考虑拿一个数据结构维护这个东西。现在要支持子树点权值和、单点修改、前缀和查询，对于每个点建立一棵动态开店线段树即可。具体的，对于点 \(x\)，下标为 \(i\) 表示 \(x\) 子树内满足 \(dis(x,p)=i\) 的 \(a_p\) 之和。这样即可求 \(l\) 的子树内距离 \(\le k-dis(x,l)\) 的点的权值和。

考虑如何求后半部分，简单粗暴一点，再建一棵线段树即可。

概括一下，两棵线段树，一棵维护到点 \(x\) 的距离的点权和，一棵维护到 \(fa_x\) 的距离的点权和。

#include <bits/stdc++.h>
#define il inline
#define int long long

using namespace std;

const int bufsz = 1 << 20;
char ibuf[bufsz], *p1 = ibuf, *p2 = ibuf;
#define getchar() (p1 == p2 && (p2 = (p1 = ibuf) + fread(ibuf, 1, bufsz, stdin), p1 == p2) ? EOF : *p1++)
il int read() {
	int x = 0; char ch = getchar(); bool t = 0;
	while (ch < '0' || ch > '9') {t ^= ch == '-'; ch = getchar();}
	while (ch >= '0' && ch <= '9') {x = (x << 1) + (x << 3) + (ch ^ 48); ch = getchar();}
	return t ? -x : x;
}
const int N = 1e5 + 10;
int n, m, a[N]; 
vector<int> G[N];
int siz[N], son[N], fa[N], dep[N], top[N];
il void dfs1(int x, int father) {
	fa[x] = father;
	dep[x] = dep[fa[x]] + 1;
	siz[x] = 1;
	for (int y : G[x]) {
		if (y == fa[x]) continue;
		dfs1(y, x);
		siz[x] += siz[y];
		if (siz[y] > siz[son[x]]) son[x] = y;
	}
}
il void dfs2(int x, int t) {
	top[x] = t;
	if (!son[x]) return;
	dfs2(son[x], t);
	for (int y : G[x]) {
		if (y == fa[x] || y == son[x]) continue;
		dfs2(y, y);
	}
}
il int getlca(int x, int y) {
	while (top[x] != top[y]) {
		if (dep[top[x]] < dep[top[y]]) swap(x, y);
		x = fa[top[x]];
	}
	if (dep[x] < dep[y]) swap(x, y);
	return y;
}
il int getdis(int x, int y) {
	return dep[x] + dep[y] - 2 * dep[getlca(x, y)];
}
struct Seg {
	struct node {
		int l, r, s;
	} tree[40 * N];
	#define lc tree[p].l
	#define rc tree[p].r
	int root[N], tot;
	il void pushup(int p) {
		tree[p].s = tree[lc].s + tree[rc].s;
	}
	il void update(int &p, int l, int r, int x, int v) {
		if (!p) p = ++tot;
		if (l == r) {
			tree[p].s += v;
			return;
		}
		int mid = l + r >> 1;
		if (x <= mid) update(lc, l, mid, x, v);
		else update(rc, mid + 1, r, x, v);
		pushup(p);
	} 
	il int query(int p, int l, int r, int x, int y) {
		if (!p || x > y) return 0;
		if (l == x && y == r) return tree[p].s;
		int mid = l + r >> 1;
		if (y <= mid) return query(lc, l, mid, x, y);
		else if (x > mid) return query(rc, mid + 1, r, x, y);
		else return query(lc, l, mid, x, mid) + query(rc, mid + 1, r, mid + 1, y);
	}
} tr1, tr2;
int cen, sz[N], sum, f[N], fl[N];
il void getcen(int x, int fa) {
	sz[x] = 1;
	int mx = 0;
	for (int y : G[x]) {
		if (fl[y] || y == fa) continue;
		getcen(y, x);
		sz[x] += sz[y];
		mx = max(mx, sz[y]);
	}
	mx = max(mx, sum - sz[x]);
	if (mx <= sum / 2) cen = x;
}
il void dfs(int x, int fr) {
	fl[x] = 1;
	for (int y : G[x]) {
		if (fl[y] || y == fr) continue;
		sum = sz[y];
		getcen(y, 0);
		getcen(cen, 0);
		f[cen] = x;
		dfs(cen, 0);
	}
}
il void update(int x, int v) {
	for (int p = x; p; p = f[p]) {
		tr1.update(tr1.root[p], 0, n, getdis(x, p), v);
		if (f[p]) {
			tr2.update(tr2.root[p], 0, n, getdis(x, f[p]), v);
		}
	}
}
il int query(int x, int k) {
	int ans = 0, pre = 0;
	for (int p = x; p; p = f[p]) {
		int len = k - getdis(x, p);
		ans += tr1.query(tr1.root[p], 0, n, 0, len) - tr2.query(tr2.root[pre], 0, n, 0, len);
		pre = p;
	}
	return ans;
}
signed main() {
	n = read(), m = read();
	for (int i = 1; i <= n; i++) a[i] = read();
	for (int i = 1; i < n; i++) {
		int x = read(), y = read();
		G[x].push_back(y);
		G[y].push_back(x);
	}
	dfs1(1, 0);
	dfs2(1, 1);
	sum = n;
	getcen(1, 0);
	getcen(cen, 0);
	dfs(cen, 0);
	for (int i = 1; i <= n; i++) {
		update(i, a[i]);
	}
	int lastans = 0;
	while (m--) {
		int op = read(), x = read(), y = read();
		x ^= lastans, y ^= lastans;
		if (op == 0) {
			printf("%lld\n", lastans = query(x, y));
		} else {
			update(x, -a[x] + y);
			a[x] = y;
		}
	}
	
	return 0;
}

posted @ 2025-08-08 08:04 Zctf1088 阅读(15) 评论(0) 收藏举报

刷新页面返回顶部

Zctf1088

路虽远，行则将至。

点分治

点分治

概念

实现

动态点分治

基本概念

例题

公告