2025CSP-S模拟赛18 比赛总结
2025CSP-S模拟赛 18
前几天题改的不是很好,先空着。
然后就是今天学习了比较牛逼的快读快写。计划是以后写题把这种读写和 ios 都打上,以备不时之需。
另外一个就是以后比赛总结写得简洁一些,这只不过是一个复盘的过程,又不是写题解。
T1 flandre
可以证明,答案最优一定是取他的一段后缀。这个举几个例子就可以说明。
然后一次考虑每一个后缀,维护答案即可。
#include <bits/stdc++.h>
#define int long long
using namespace std;
int read() {
int x = 0, f = 1; char ch = getchar();
while (ch < '0' || ch > '9') {
if (ch == '-') f = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9') {
x = (x << 1) + (x << 3) + (ch ^ 48);
ch = getchar();
}
return x * f;
}
const int INF = 0x3f3f3f3f3f3f3f3f;
const int N = 1e6 + 10;
int n, kk;
struct node {
int a, id;
bool operator < (const node & cmp) const {
return a < cmp.a;
}
} e[N];
unordered_map<int, int> len;
signed main() {
n = read(), kk = read();
for (int i = 1; i <= n; i++) {
e[i].a = read();
e[i].id = i;
}
sort(e + 1, e + 1 + n);
int ans = -INF, id = 1;
int now = 0;
for (int i = n; i >= 1; i--) {
now += e[i].a + kk * (n - i - len[e[i].a]);
len[e[i].a]++;
if (now > ans) {
ans = now;
id = i;
}
}
printf("%lld %lld\n", ans, n - id + 1);
for (int i = id; i <= n; i++) {
printf("%lld ", e[i].id);
}
return 0;
}
T2 meirin
这题场上切了。
考虑拆贡献。考虑每个 \(b_i\) 对于答案的贡献:
\[\begin{array}{ll}
ans & = & \sum_{l=1}^n\sum_{r=l}^n(\sum_{i=l}^ra_i)\times(\sum_{i=l}^rb_i) \\
& = & \sum_{i=1}^nb_i(\sum_{l=1}^i\sum_{r=i}^n\sum_{j=l}^ra_j)\\
& = & \sum_{i=1}^nb_i(\sum_{l=1}^i\sum_{r=i}^n(sa_r-sa_{l-1}))\\
& = & \sum_{i=1}^nb_i((\sum_{l=1}^i\sum_{r=i}^nsa_r)-(\sum_{l=1}^i\sum_{r=i}^nsa_{l-1}))\\
& = & \sum_{i=1}^nb_i((i\sum_{r=i}^nsa_r)-((n-i+1)\sum_{l=0}^{i-1}sa_l))\\
\end{array}
\]
其中 \(sa_i\) 为 \(a\) 的前缀和。
令 \(f_i\) 表示 \(b_i\) 后面这一坨,即 \(f_i=(i\sum_{r=i}^nsa_r)-((n-i+1)\sum_{l=0}^{i-1}sa_l)\)。如何求?给 \(sa\) 求个前缀和即可 \(O(n)\) 求出。则:
\[ans=\sum_{i=1}^nf_ib_i
\]
每次修改给 \(l\) 到 \(r\) 的 \(b_i\) 加上 \(k\),则答案增加的值即为 \(k\sum_{i=l}^rf_i\)。对 \(f_i\) 求前缀和即可每次操作 \(O(1)\) 修改。
#include <bits/stdc++.h>
#define int long long
using namespace std;
namespace IO {
const int bufsz = 1 << 20;
char ibuf[bufsz], *p1 = ibuf, *p2 = ibuf;
char obuf[bufsz], *p3 = obuf, stk[50];
#define getchar() (p1 == p2 && (p2 = (p1 = ibuf) + fread(ibuf, 1, bufsz, stdin), p1 == p2) ? EOF : *p1++)
#define flush() (fwrite(obuf, 1, p3 - obuf, stdout), p3 = obuf)
#define putchar(ch) (p3 == obuf + bufsz && flush(), *p3++ = (ch))
inline int read() {
int x = 0; char ch = getchar(); bool t = 0;
while (ch < '0' || ch > '9') {t ^= ch == '-'; ch = getchar();}
while (ch >= '0' && ch <= '9') {x = (x << 1) + (x << 3) + (ch ^ 48); ch = getchar();}
return t ? -x : x;
}
inline void write(int x, bool t = 1) {
int top = 0;
do {stk[++top] = x % 10 | 48; x /= 10;} while (x);
while (top) putchar(stk[top--]);
t ? putchar('\n') : putchar(' ');
}
struct FL {~FL() {flush();}} fl;
#undef getchar()
#undef putchar()
#undef flush()
}
using IO::read;
using IO::write;
const int MOD = 1e9 + 7;
const int N = 5e5 + 10;
int n, qq, a[N], b[N];
int s[N], f[N], ss[N], sf[N];
signed main() {
n = read(), qq = read();
for (int i = 1; i <= n; i++) a[i] = read();
for (int i = 1; i <= n; i++) b[i] = read();
for (int i = 1; i <= n; i++) {
s[i] = (s[i - 1] + a[i]) % MOD;
ss[i] = (ss[i - 1] + s[i]) % MOD;
}
for (int i = 1; i <= n; i++) {
f[i] = ((ss[n] - ss[i - 1]) % MOD * i % MOD - ss[i - 1] * (n - i + 1) % MOD) % MOD;
sf[i] = (sf[i - 1] + f[i]) % MOD;
}
int ans = 0;
for (int i = 1; i <= n; i++) {
ans = (ans + b[i] * f[i] % MOD) % MOD;
}
while (qq--) {
int l = read(), r = read(), k = read();
ans = (ans + (sf[r] - sf[l - 1]) % MOD * k % MOD) % MOD;
write((ans + MOD) % MOD);
}
return 0;
}
T3 sakuya
考虑拆贡献。
考虑每条边对于答案的贡献。首先树形 dp 求出初始的贡献,即为 \(w_i\times num_i\)。其中 \(w\) 为边权,\(num\) 为这条边左右特殊点个数的乘积。然后当一条边的边权加上 \(k\),对答案增加的贡献即为 \(k\times num_i\)。对于每个点统计发出的所有边的 \(num\) 然后 \(O(1)\) 进行维护答案即可。
#include <bits/stdc++.h>
#define int long long
using namespace std;
namespace IO {
// 这里的读写这么怪是因为当时数据锅了,快读过不了,只有 cin cout 能过,方便调试。不必在意。
inline int read() {
int x;
cin >> x;
return x;
}
inline void write(int x, bool t = 1) {
cout << x << '\n';
}
}
using IO::read;
using IO::write;
const int MOD = 998244353;
const int N = 5e5 + 10;
int n, m, qq, a[N];
struct edge {
int y, w;
};
vector<edge> G[N];
int fpow(int a, int x) {
a %= MOD;
int ans = 1;
while (x) {
if (x & 1) ans = ans * a % MOD;
a = a * a % MOD;
x >>= 1;
}
return ans;
}
int fact[N];
int fa[N];
int f[N], g[N], dp[N], ans;
void dfs(int x, int father) {
fa[x] = father;
for (edge i : G[x]) {
int y = i.y;
if (y == fa[x]) continue;
dfs(y, x);
f[x] += f[y];
ans = (ans + g[y] * i.w % MOD) % MOD;
dp[x] = (dp[x] + g[y]) % MOD;
}
g[x] = f[x] * (m - f[x]) % MOD * 2 % MOD * fact[m - 1] % MOD;
dp[x] = (dp[x] + g[x]) % MOD;
}
signed main() {
ios::sync_with_stdio(0); cin.tie(0), cout.tie(0);
n = read(), m = read();
for (int i = 1; i < n; i++) {
int x = read(), y = read(), z = read();
G[x].push_back({y, z});
G[y].push_back({x, z});
}
for (int i = 1; i <= m; i++) {
a[i] = read();
f[a[i]] = 1;
}
fact[0] = 1;
for (int i = 1; i <= m; i++) fact[i] = fact[i - 1] * i % MOD;
int ny = fpow(fact[m], MOD - 2);
dfs(1, 0);
ans = (ans + MOD) % MOD;
qq = read();
while (qq--) {
int x = read(), k = read();
ans = (ans + dp[x] * k % MOD) % MOD;
write(ans * ny % MOD);
}
return 0;
}
T4 红楼 ~ Eastern Dream
一眼根号分治。

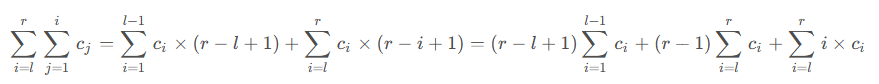

懒得写了,直接截图。
#include <bits/stdc++.h>
#define il inline
#define int long long
using namespace std;
namespace IO {
const int bufsz = 1 << 20;
char ibuf[bufsz], *p1 = ibuf, *p2 = ibuf;
char obuf[bufsz], *p3 = obuf, stk[50];
#define getchar() (p1 == p2 && (p2 = (p1 = ibuf) + fread(ibuf, 1, bufsz, stdin), p1 == p2) ? EOF : *p1++)
#define flush() (fwrite(obuf, 1, p3 - obuf, stdout), p3 = obuf)
#define putchar(ch) (p3 == obuf + bufsz && flush(), *p3++ = (ch))
inline int read() {
int x = 0; char ch = getchar(); bool t = 0;
while (ch < '0' || ch > '9') {t ^= ch == '-'; ch = getchar();}
while (ch >= '0' && ch <= '9') {x = (x << 1) + (x << 3) + (ch ^ 48); ch = getchar();}
return t ? -x : x;
}
inline void write(int x, bool t = 1) {
int top = 0;
do {stk[++top] = x % 10 | 48; x /= 10;} while (x);
while (top) putchar(stk[top--]);
t ? putchar('\n') : putchar(' ');
}
struct FL {~FL() {flush();}} fl;
#undef getchar()
#undef putchar()
#undef flush()
}
using IO::read;
using IO::write;
const int N = 2e5 + 10, M = 500;
int n, m, a[N], sq;
int s[N];
int v[M][M], sv[M][M], c[N], ic[N];
int st[M], ed[M], beg[N], cc[N], icc[N];
il void init() {
for (int i = 1; i <= sq; i++) {
st[i] = n / sq * (i - 1) + 1;
ed[i] = n / sq * i;
}
ed[sq] = n;
for (int i = 1; i <= sq; i++) {
for (int j = st[i]; j <= ed[i]; j++) {
beg[j] = i;
}
}
}
il void update(int p, int x) {
c[p] += x;
cc[beg[p]] += x;
ic[p] += x * p;
icc[beg[p]] += x * p;
}
il int query(int l, int r) {
if (l > r) return 0;
if (beg[l] == beg[r]) {
int res = 0;
for (int i = l; i <= r; i++) res += c[i];
return res;
}
int res = 0;
for (int i = l; i <= ed[beg[l]]; i++) res += c[i];
for (int i = st[beg[r]]; i <= r; i++) res += c[i];
for (int i = beg[l] + 1; i < beg[r]; i++) {
res += cc[i];
}
return res;
}
il int queryi(int l, int r) {
if (l > r) return 0;
if (beg[l] == beg[r]) {
int res = 0;
for (int i = l; i <= r; i++) res += ic[i];
return res;
}
int res = 0;
for (int i = l; i <= ed[beg[l]]; i++) res += ic[i];
for (int i = st[beg[r]]; i <= r; i++) res += ic[i];
for (int i = beg[l] + 1; i < beg[r]; i++) {
res += icc[i];
}
return res;
}
signed main() {
n = read(), m = read();
for (int i = 1; i <= n; i++) a[i] = read();
for (int i = 1; i <= n; i++) s[i] = s[i - 1] + a[i];
sq = sqrt(n);
init();
while (m--) {
int op = read();
if (op == 1) {
int x = read(), y = read(), k = read();
y = min(x - 1, y);
if (x <= sq) {
for (int i = 0; i <= y; i++) {
v[x][i] += k;
}
sv[x][0] = v[x][0];
for (int i = 1; i < x; i++) {
sv[x][i] = sv[x][i - 1] + v[x][i];
}
} else {
for (int i = 1; i <= n; i += x) {
update(i, k);
update(min(n + 1, i + y + 1), -k);
}
}
} else {
int l = read(), r = read();
int ans = s[r] - s[l - 1];
for (int i = 1; i <= sq; i++) {
ans += sv[i][(r - 1) % i];
ans -= sv[i][(l - 1) % i - 1];
int ll = (l - 1) / i, rr = (r - 1) / i;
ans += (rr - ll) * sv[i][i - 1];
}
ans += (r - l + 1) * query(1, l - 1) + (r + 1) * query(l, r) - queryi(l, r);
printf("%lld\n", ans);
}
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号