2025CSP-S模拟赛14 比赛总结

2025CSP-S模拟赛14

T1 魔力屏障

基础思路

首先我们注意到一个东西，就是任何时刻都选择恰好能击破当前屏障的一定是最优的。因为如果当前花费更多代价，后面这部分会减半，还不如在后面在放上多出的这部分。

然后有一个事情，我们从样例中就能看出，从前往后逐个击破不一定是最优的。

依次，我们考虑区间 dp。

考虑 \(f_{i,j,k}\) 表示 \(i\) 到 \(j\) 这段区间击破后还剩一个 \(k\) 的魔力值的攻击，的最小花费。答案即为 \(\min f_{1,i,k}\)。初始化 \(f_{i,i,a[i]/2}=a[i]\)。

考虑转移。效仿经典的区间 dp，考虑枚举断点 \(m\) 以及前一半即 \([i,m]\) 击破后剩余的攻击值 \(v\)，那么后一半即 \([m+1,j]\) 的剩余攻击值即为 \(k-v\)。写下来就是：

\[f_{i,j,k}=\min_{i\le m < j} \min_{0 \le v \le k} \{f_{i,m,v}+f_{m+1,j,k-v}\} \]

然后考虑把剩余的攻击累加到后续的攻击中。不妨设 \([l,r-1]\) 剩余的攻击值为 \(p\)，那么此时击破下一个屏障只需额外花费 \(\max\{0,a_r-p\}\)。简单处理即可。

复杂度分析

可以发现 \(k\) 一定小于等于 \(\sum a_i\)，因为答案至多为 \(\sum a_i\)。

然后考虑到在任意时刻的魔力值一定不会多于当前的 \(a_i\)，类似之前的思考方式，多出的在后面会减半。所以我们在枚举 \(k\) 的时候保证 \(k \le \max a_i\) 即可。

记 \(V=\max a_i\)，时间复杂度为 \(O(n^3V^2)\)。外加带有 \(\frac{1}{8}\) 小常数，可以通过本题。

#include <bits/stdc++.h>

using namespace std;

int read() {
	int x = 0; char ch = getchar();
	while (ch < '0' || ch > '9') ch = getchar();
	while (ch >= '0' && ch <= '9') {
		x = (x << 1) + (x << 3) + (ch ^ 48);
		ch = getchar();
	}
	return x;
}
#define min(x, y) (x < y ? x : y)
#define max(x, y) (x > y ? x : y)
const int INF = 0x3f3f3f3f;
const int N = 70 + 2, M = 150 + 2;
int n, a[N];
int f[N][N][M];
int main() {
	n = read();
	int mx = 0;
	for (int i = 1; i <= n; i++) {
		a[i] = read();
		mx = max(mx, a[i]);
	}
	for (int i = 1; i <= n; i++) 
		for (int j = 1; j <= n; j++) 
			for (int k = 0; k <= mx; k++) 
				f[i][j][k] = INF;
	for (int i = 1; i <= n; i++) {
		f[i][i][a[i] >> 1] = a[i];
	}
	for (int len = 2; len <= n; len++) {
		for (int i = 1; i + len - 1 <= n; i++) {
			int j = i + len - 1;
			for (int k = 0; k <= mx; k++) {
				for (int m = i; m < j; m++) {
					for (int v = 0; v <= k; v++) {
						f[i][j][k] = min(f[i][j][k], f[i][m][v] + f[m + 1][j][k - v]); 
					}
				}
			}
			for (int v = 0; v < a[j]; v++) {
				f[i][j][a[j] >> 1] = min(f[i][j][a[j] >> 1], f[i][j - 1][v] + a[j] - v);
			}
			for (int v = a[j]; v <= mx; v++) {
				f[i][j][v >> 1] = min(f[i][j][v >> 1], f[i][j - 1][v]);
			}
		}
	}
	for (int i = 1; i <= n; i++) {
		int ans = INF;
		for (int k = 0; k <= mx; k++) {
			ans = min(ans, f[1][i][k]);
		}
		printf("%d ", ans);
	}
	
	return 0;
}

T2 诡秘之主

咕

T3 博弈

又是博弈论。这次和上次不一样，起码有个基本的大概思路，虽然没什么用。

直接看正解。

首先考虑以 \(T\) 为根重建树。那么问题转化为要走到根节点。

先考虑存在边 \((S,T)\) 的情况。如果小 Y 不做任何操作的话，那么小 N 的最优策略就是向叶子节点走到底。然后此时小 N 动不了了，小 Y 的最优策略就是通过断边和恢复边把小 N 赶到根节点。

设 \(f_v\) 表示在以 \(v\) 为根的子树中，初始小 N 从 \(v\) 出发，最后被迫回到 \(v\) 的最小代价。考虑在 \(u\) 的子树中，小 N 最优一定是走 \(f_v\) 最大的一个儿子，那么小 Y 就会堵住这个儿子，那么小 N 就会走第二大的。则：

\[f_u=2\text{nd}\max_{v\in son_u} \{1+f_v+|son_u|-1\} \]

这里把 \(-1\) 和 \(+1\) 分开写是便于理解。

现在考虑对于一般情况。一般情况下，小 N 会先向根的方向走一段距离，再向叶子的方向走。

考虑将最优化问题转化为判定问题。现在钦定一个小 Y 的总操作次数 \(M\)，看能否在 \(M\) 次内结束博弈（把小 N 赶到根节点）。

考虑用 \(g_u\) 表示从 \(u\) 到根节点一路上分岔路的数量（不记根链）。\(f\) 和 \(g\) 都可以通过一次 dfs 得到。

现在，我们模拟从 \(S\) 走到根的过程。当位于点 \(u\) 的时候，如果有一个儿子 \(v \in son_u\)，使得 \(g_u+f_v+cnt>M\)（其中 \(cnt\) 为此前的操作次数），即如果小 N 从 \(v\) 走下去我们再把他赶上来的总代价大于总操作次数，那么就一定不能让他从 \(v\) 走，于是就要把 \((u,v)\) 这条边断掉。

当当前的操作次数大于总操作次数时或大于可操作次数时（由于两人时轮流操作的），不合法。

没了。

然后就是由于每条边最多被删一次加一次，所以最多操作 \(2n\) 次。

显然 \(M\) 是具有单调性的，所以可以使用二分答案。时间复杂度 \(O(n\log n)\)。

#include <bits/stdc++.h>

using namespace std;

int read() {
	int x = 0; char ch = getchar();
	while (ch < '0' || ch > '9') ch = getchar();
	while (ch >= '0' && ch <= '9') {
		x = (x << 1) + (x << 3) + (ch ^ 48);
		ch = getchar();
	}
	return x;
}
const int P = 131;
const int INF = 0x3f3f3f3f;
const int N = 1e6 + 10;
int n, T, S;
vector<int> G[N];
int f[N], g[N], fa[N], dep[N];
void dfs(int x, int father) {
	fa[x] = father;
	dep[x] = dep[fa[x]] + 1;
	if (fa[x] != 0) g[x] = g[fa[x]] + (G[x].size() - 2);
	int mx = 0, mxx = 0;
	for (int y : G[x]) {
		if (y == fa[x]) continue;
		dfs(y, x);
		if (f[y] > mx) {
			mxx = mx;
			mx = f[y];
		} else if (f[y] > mxx) {
			mxx = f[y];
		}
	}
	f[x] = mxx + (G[x].size() - (fa[x] != 0));
}
bool check(int ops) {
	int cnt = 0, lst = -1;	// cnt 是当前操作次数
	int tim = 0;			// tim 是当前可操作次数
	for (int x = S; x != T; x = fa[x]) {
		tim++;
		int tmp = cnt;
		for (int y : G[x]) {
			if (y != lst && y != fa[x] && g[x] + f[y] + tmp + (lst == -1) > ops) {
				cnt++;
			}
		}
		if (cnt > tim || cnt > ops) return false;
		lst = x;
	}
	return true;
}
int main() {
	n = read(), T = read(), S = read();
	if (T == S || n <= 2) {
		printf("0\n");
		return 0;
	}
	for (int i = 1; i < n; i++) {
		int x = read(), y = read();
		G[x].push_back(y);
		G[y].push_back(x);
	}
	dfs(T, 0);
	int l = 0, r = 2 * n, ans = 0;
	while (l <= r) {
		int mid = l + r >> 1;
		if (check(mid)) {
			ans = mid;
			r = mid - 1;
		} else {
			l = mid + 1;
		}
	}
	printf("%d\n", ans);
	
	return 0;
}

T4 地雷

这个区间 dp 还是很牛逼了。

直接来看正解。

考虑区间 dp。设 \(f_{i,j,t,u}\) 表示当前考虑区间 \([i,j]\)，满足 \(i-1,j-1\) 都比 \([i,j]\) 更晚删除，在 \(j+1\) 后第一个比 \([i,j]\) 更晚删除的数的下标是 \(t\)。同时，\(u\) 是一些限制条件，需要保证区间中 \(u\) 左侧的数都比 \(u\) 更早删除，\(u \in[i,j+1]\)。\(f\) 就是满足上述条件的区间 \([i,j]\) 的最大删除代价。

枚举 \(k \in[i,j]\)，枚举对于 \(k\) 而言左侧区间的 \(t\)（设为 \(v\)），根据 \(u\) 的定义，\(k\) 必须 \(\geq u\)。\(v\in[k+1,j+1]\)。

综上，整理出来一个图，反映数（区间）大致的空间分布以及被删除顺序：

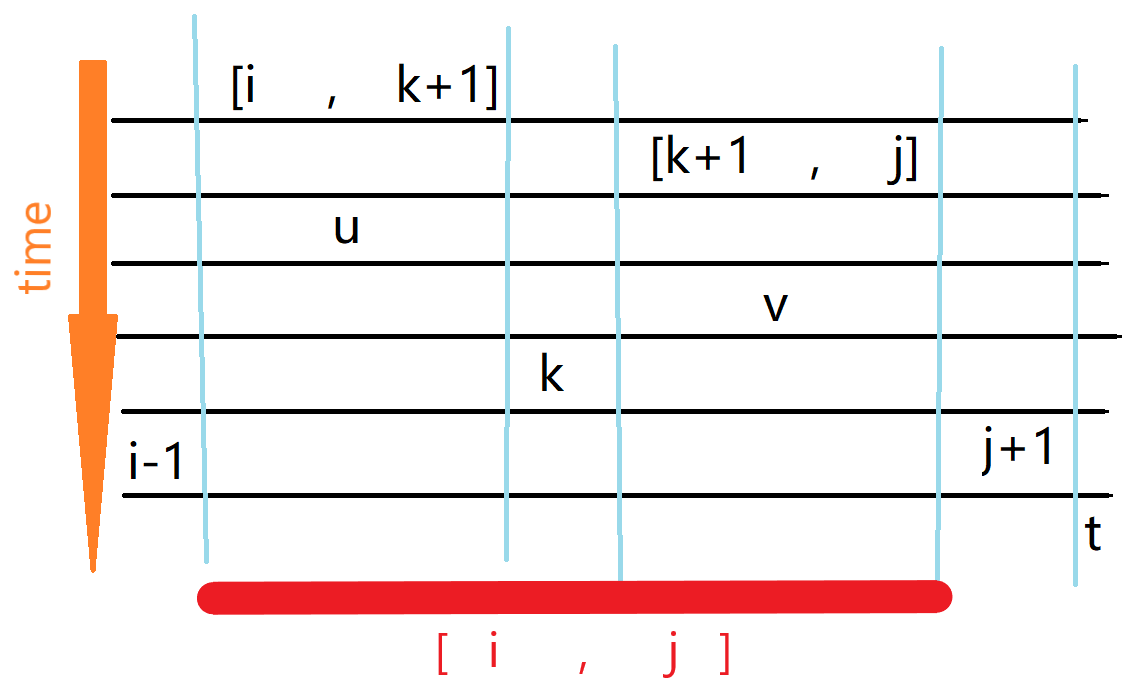
转移：

\[f_{i,j,t,u}=\max_{u\le k\le j,k+1\le v \le j+1}\{f_{i,k-1,v,u}+f_{k+1,j,t,v}+val(i-1,k,j+1,t)\} \]

其中

\[val(a,b,c,d)=(p_a-q_b)^2+(p_b-r_c)^2+(p_c-s_d)^2 \]

那就是这样。题解还有一堆解释，我觉得没必要了，这一个图就很清晰了。

这里附上题解剩下的话：

#include <bits/stdc++.h>

using namespace std;

int read() {
	int x = 0, f = 1; char ch = getchar();
	while (ch < '0' || ch > '9') {
		if (ch == '-') f = -1;
		ch = getchar();
	}
	while (ch >= '0' && ch <= '9') {
		x = (x << 1) + (x << 3) + (ch ^ 48);
		ch = getchar();
	}
	return x * f;
}
const int INF = 0x3f3f3f3f;
const int N = 70 + 5;
int n, p[N], q[N], r[N], s[N];
int f[N][N][N][N];
inline int S(int x) {
	return x * x;
}
inline int solve(int a, int b, int c, int d) {
	return S(p[a] - q[b]) + S(p[b] - r[c]) + S(p[c] - s[d]);
}
int main() {
	n = read();
	for (int i = 1; i <= n; i++) p[i] = read();
	for (int i = 1; i <= n; i++) q[i] = read();
	for (int i = 1; i <= n; i++) r[i] = read();
	for (int i = 1; i <= n; i++) s[i] = read();
	for (int i = 0; i < N; i++)
		for (int j = 0; j < N; j++) 
			for (int t = 0; t < N; t++)
				for (int u = 0; u < N; u++) f[i][j][t][u] = -INF;
	for (int i = 1; i <= n + 2; i++) {
		for (int t = i + 2; t <= n + 2; t++) {
			f[i][i][t][i] = f[i][i][t][i + 1] = solve(i - 1, i, i + 1, t);
		} 
		for (int t = i + 1; t <= n + 2; t++) {
			f[i][i - 1][t][i] = 0;
		}
	}
	for (int len = 2; len <= n; len++) {
		for (int i = 1; i + len - 1 <= n; i++) {
			int j = i + len - 1;
			for (int t = j + 2; t <= n + 2; t++) {
				for (int u = i; u <= j + 1; u++) {
					for (int k = u; k <= j; k++) {
						int val = solve(i - 1, k, j + 1, t);
						int x = (u == k ? i : u);
						f[i][j][t][u] = max(f[i][j][t][u], f[i][k - 1][j + 1][x] + f[k + 1][j][t][k + 1] + val);
						for (int v = k + 1; v <= j + 1; v++) {
							f[i][j][t][u] = max(f[i][j][t][u], f[i][k - 1][v][x] + f[k + 1][j][t][v] + val);
						}
					}
				}
			}
		}
	}
	printf("%d\n", f[1][n][n + 2][1]);
	
	return 0;
}