2025CSP-S模拟赛4 比赛总结
2025CSP-S模拟赛4
一场比赛四个题两个原,T2T3 统统挂完。想死吗?
T1 序列问题
首先,对于 \(O(n^2)\) 的 dp 是简单的。赛时是设 \(f_{i,j}\) 表示考虑到第 \(i\) 个数,且他排在 \(B\) 中的第 \(j\) 位。但是最后又滚又优化最多就是 \(O(n^2)\) 了,没法再优化。
考虑正解。设 \(f_i\) 表示考虑到 \(B\) 中第 \(i\) 个数且以 \(a_i\) 结尾。则需满足:1. \(j<i\),2. \(a_j<a_i\),3. \(a_i-a_j \le i-j\) 三个条件才可以转移。另外需要注意,当且仅当 \(a_i \le i\) 时 \(f_i\) 才是合法的。那么转移很简单了:
时间复杂度 \(O(n^2)\)。
然后考虑 \(a_i-a_j \le i-j\) 可以写成 \(j-a_j \le i-a_i\)。再次观察这三个条件:
- \(j<i\)
- \(a_j<a_i\)
- \(j-a_j \le i-a_i\)
注意到当满足后两个条件的时候第一个条件一定满足。于是我们可以把原序列按照 \(a_i\) 排序,然后就是一个对于 \(i-a_i\) 的最长不降子序列问题了。
注意:为避免 \(a_j=a_i\) 的尴尬情况,排序的时候第二关键字(原序列下标)按降序排列。
#include <bits/stdc++.h>
#define int long long
using namespace std;
int read() {
int x = 0; char ch = getchar();
while (ch < '0' || ch > '9') ch = getchar();
while (ch >= '0' && ch <= '9') {
x = (x << 1) + (x << 3) + (ch ^ 48);
ch = getchar();
}
return x;
}
const int N = 5e5 + 10;
int n;
int f[N];
struct node {
int id, v;
bool operator < (const node & cmp) const {
return v != cmp.v ? v < cmp.v : id > cmp.id;
}
} a[N];
int c[N];
void update(int x, int v) {
x++;
for (int i = x; i <= n; i += (i & -i)) {
c[i] = max(c[i], v);
}
}
int query(int x) {
x++;
int ans = 0;
for (int i = x; i; i -= (i & -i)) {
ans = max(ans, c[i]);
}
return ans;
}
signed main() {
freopen("sequence.in", "r", stdin);
freopen("sequence.out", "w", stdout);
n = read();
for (int i = 1; i <= n; i++) {
a[i] = {i, read()};
}
sort(a + 1, a + 1 + n);
int ans = 0;
for (int i = 1; i <= n; i++) {
if (a[i].v > a[i].id) continue;
f[i] = query(a[i].id - a[i].v) + 1;
ans = max(ans, f[i]);
update(a[i].id - a[i].v, f[i]);
}
printf("%lld\n", ans);
return 0;
}
T2 钱仓
原。
引入一下。这边有一个 \(n^2\) 过十万的代码:
const int INF = 0x3f3f3f3f3f3f3f3f;
const int N = 2e5 + 10;
int n, a[N];
int q[N], head, tail;
int v[N];
signed main() {
freopen("barn.in", "r", stdin);
freopen("barn.out", "w", stdout);
n = read();
for (int i = 1; i <= n; i++) {
a[i] = a[i + n] = read();
}
int ans = INF;
for (int j = 1; j <= n; j++) {
if (a[j] == 1) continue; // 小优化
head = 1, tail = 0;
long long sum = 0;
for (int i = j; i <= j + n - 1; i++) {
if (a[i]) {
++tail;
q[tail] = i;
v[tail] = a[i];
}
if (head > tail) {
sum = INF;
break;
}
sum += (q[head] - i) * (q[head] - i);
v[head]--;
if (!v[head]) head++;
}
ans = min(ans, sum);
}
printf("%lld\n", ans);
return 0;
}
现在来分析这道题。
首先有一个 \(O(n^2)\) 暴力的思路,就是我们枚举断点,然后跑贪心。具体的,每一次贪心,我们维护一个队列,当我们需要一个货物时,便从队列首取一个来用。证明很简单:\((x+y)^2\ge x^2+y^2\)。自行理解。代码的话就是上面这篇代码。
然后我发现我之前 A 掉这道题的代码是一个疑似 \(n^2\) 实则跑得飞快的代码,在当时显然并没有理解这篇代码。现在来仔细理解一下:
int ans = INF;
//cout << "beg "; for (int i = 1; i <= 2 * n; i++) cout << a[i] << " "; cout << "\n";
for (int j = 1; j <= n; j++) {
// printf("%2lld: ", j); for (int i = 1; i <= 2 * n; i++) cout << a[i] << " ";
head = 1, tail = 0;
long long sum = 0;
for (int i = j; i <= j + n - 1; i++) {
if (a[i]) q[++tail] = i;
if (head > tail) {
sum = INF;
break; // (1)
}
sum += (q[head] - i) * (q[head] - i);
a[q[head]]--;
if (!a[q[head]]) head++;
}
// (2)
ans = min(ans, sum);
// cout << " | " << sum << "\n";
}
printf("%lld\n", ans);
第一篇代码是 700ms,第二篇却只跑了 40 多ms。需要思考的便是:为什么可以在原数组 \(a\) 上去减还没有加回来是有正确性的?
先看如上代码注释中的输出:
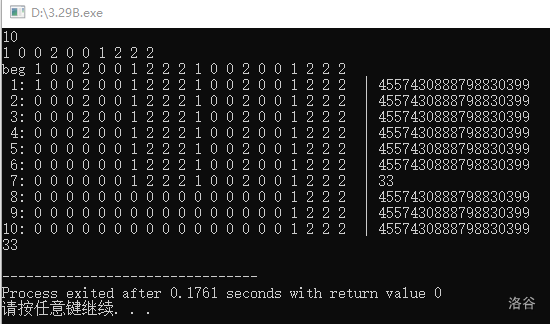
不难发现,我们每次从 (1) 处 break 掉或者正常运行到 (2) 后,都会把处理过的一段序列全部变为 0。那么就有这么一个事儿,叫做一共会跑一次且仅有一次完整的贪心。
可以这么想,一个数会影响他之后的一段区间(不一定紧挨着他)。如图给出的这组数据手玩一下大概就是这个样子:

以这种方案去分配,答案恰好是 \(1+1+4+4+9+9+1+4=33\)。这张图也可以印证“一个数影响他之后的一段区间”。
这句话有什么用呢?
把这个序列拆成数个小序列的组合,就可以得到:如果把某个小序列拆开,那么一定无法合法分配。于是,便可以提出一个大胆的结论:只要我们找到了一个合法的分配方式,此就是最优答案。
根据这种思路,如下代码也可以 AC:
int ans = INF;
for (int j = 1; j <= n; j++) {
head = 1, tail = 0;
long long sum = 0;
for (int i = j; i <= j + n - 1; i++) {
if (a[i]) {
++tail;
q[tail] = i;
v[tail] = a[i];
}
if (head > tail) {
sum = INF;
break;
}
sum += (q[head] - i) * (q[head] - i);
v[head]--;
if (!v[head]) head++;
}
if (sum < INF) {
ans = sum;
break;
}
}
printf("%lld\n", ans);
时间复杂度方面,最多对于对每个数操作一次(变为0),最多跑一次完整的贪心,故时间复杂度 \(O(n)\)。
至此,笔者认为,已经搞清楚了这道题。如有疑问,请向笔者提出,共同探讨。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号