杂项

Kurskal 重构树

定义

Kurskal 重构树就是在跑 Kurskal 的时候处理出一棵树，这棵树会有一些奇妙的性质。

考虑如何构建。

首先新建 \(n\) 个集合，每个集合前有一个节点，点权为 \(0\)。

每一次加边会合并两个集合，我们就可以新建一个点，点权为加入边的边权，同时将两个集合的根节点分别设为新建点的左右儿子。然后我们把这两个集合和新建点合并成一个集合。新建点设为根。

如此，我们就得到了一棵树。这棵树就叫作 Kurskal 重构树。

举个例子：

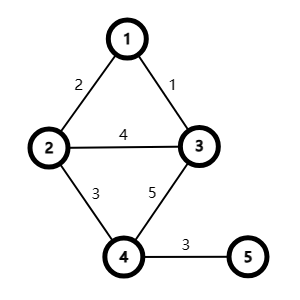
如上这张图的 Kurskal 生成树就为如下这棵树：

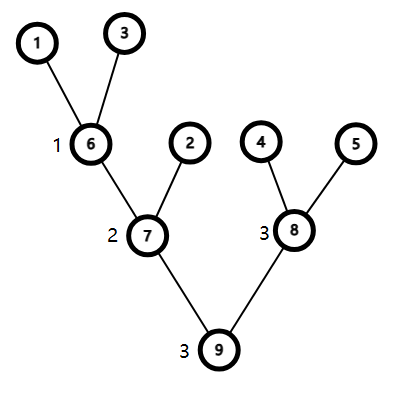
性质

由于一共进行了 \(n-1\) 次加边，即新加入 \(n-1\) 个点，所以 Kurskal 生成树的点数就为 \(2n-1\)。

不难发现，原图中两个点之间的所有 简单路径上的最大值 的最小值 = 最小生成树上两个点路径上的最大值 = Kurskal 生成树上两个点的 LCA 的点权。

参考代码

for (int i = 1; i <= n; i++) fa[i] = i, rt[i] = i;
tot = n;
for (int i = 1; i <= m; i++) {
	int x = getfa(e[i].x), y = getfa(e[i].y);
	if (x != y) {
		fa[y] = x;
		tot++;
		G[tot].push_back(rt[x]);
		G[tot].push_back(rt[y]);
		rt[x] = rt[y] = tot;
		val[tot] = e[i].w;
	}
}

ST 表 + 欧拉序求 LCA

概述

这个东西呢，比较帅。 \(O(n\log n)\) 预处理，\(O(1)\) 查询。

首先明确 ST 表的功能：\(O(n\log n)\) 预处理， \(O(1)\) 查询徐建最值。

其次，说一下欧拉序。就是在每次经过这个节点的时候都把他加入到序列末尾。比如这么一棵树，他的欧拉序就是 \(1,2,3,2,4,5,4,6,4,2,1,7,1\)。不难发现，\(n\) 个点的树的欧拉序长度为 \(2n-1\)。

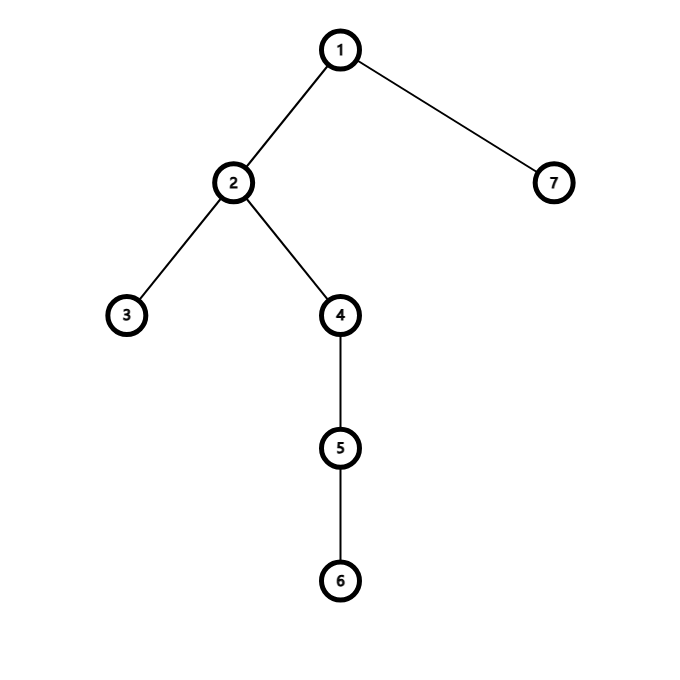
除了欧拉序之外，我们还需要一个 dfs 序（就是长度为 \(n\) 的那个）。需要注意，欧拉序和 dfs 序公用一个时间戳。

然后呢，对于两个点 \(x\)，\(y\)，我们找到他们在欧拉序中第一次出现的位置（可以拿 dfs 序直接找到），那么这两个位置之间深度最小的点即为 \(x\) 和 \(y\) 的 lca。

接下来随便怎么搞一搞就好了。

参考代码

int dfn[N], id[2 * N], tot;
void dfs(int x) {
	id[++tot] = x;
	dfn[x] = tot;
	for (int y : G[x]) {
		dfs(y);
		id[++tot] = x;
	}
}
int Log2[2 * N], f[2 * N][18];
void init() {
	for (int i = 2; i <= tot; i++) Log2[i] = Log2[i / 2] + 1;
	for (int i = 1; i <= tot; i++) f[i][0] = dfn[id[i]];
	for (int j = 1; j <= Log2[tot]; j++) {
		for (int i = 1; i + (1 << j) - 1 <= tot; i++) {
			f[i][j] = min(f[i][j - 1], f[i + (1 << j - 1)][j - 1]);
		}
	}
}
int getlca(int x, int y) {
	if (dfn[x] > dfn[y]) swap(x, y);
	int s = Log2[dfn[y] - dfn[x] + 1];
	return id[min(f[dfn[x]][s], f[dfn[y] - (1 << s) + 1][s])];
}