笛卡尔树

笛卡尔树

定义

笛卡尔树就是一种二叉树。笛卡尔树的每一个节点由一个二元组 \((k,w)\) 构成。要求 \(k\) 满足二叉搜索树^[1]的性质，\(w\) 满足堆^[2]的性质。当 \(w\) 的值随机时，这就是一颗 Treap。

Treap 和笛卡尔树

Treap 是笛卡尔树中的一种，只不过 Treap 中的 \(w\) 完全随机。或者说，Treap 是平衡的笛卡尔树。

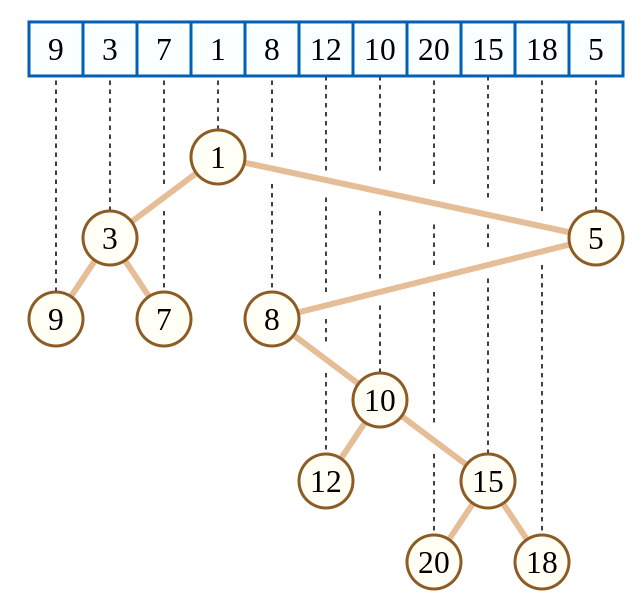
如图这颗笛卡尔树把下标作为 \(k\)，把数组元素值作为 \(w\)。不难发现， \(k\) 满足二叉搜索树的性质， \(w\) 满足小根堆的性质。根据二叉搜索树的性质，可以发现这种笛卡尔树满足一棵子树内的下标时一个连续的区间。

建树

考虑按照下标将点依次插入到当前的笛卡尔树中。那么我们每次插入元素必然在这棵树右链的末端。假设我们维护的时小根堆。那么我们不妨把右链看作一个单调递增的单调栈，去把当前点插入到合适的位置，把比他大的点就作为他的左儿子。

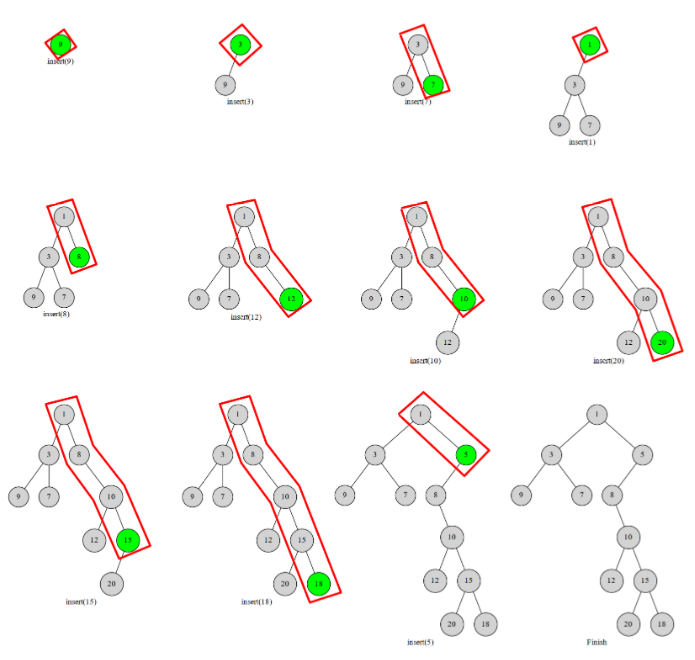
代码实现

int n, a[N];
int st[N], head; // 维护单调栈
int ls[N], rs[N]; // 存储每个点的左儿子和右儿子
int main() {
	n = read(); 
	for (int i = 1; i <= n; i++) {
		a[i] = read();
	}
	for (int i = 1; i <= n; i++) {
		int k = head;
		while (k && a[st[k]] > a[i]) k--; // 维护单调栈
		if (k) rs[st[k]] = i;
		if (k < head) ls[i] = st[k + 1];
		st[++k] = i;
		head = k;
	}
	
	return 0;
}

例题

P5854 【模板】笛卡尔树

根据给出的数组构建一颗笛卡尔树（二叉搜索树+小根堆）。设 \(l_i,r_i\) 分别表示节点 \(i\) 的左右儿子的编号（若不存在则为 \(0\)）。一行两个整数，分别表示 \(\operatorname{xor}_{i = 1}^n i \times (l_i + 1)\) 和 \(\operatorname{xor}_{i = 1}^n i \times (r_i + 1)\)。

#include <bits/stdc++.h>
#define int long long

using namespace std;

int read() {
	int x = 0; char ch = getchar();
	while (ch < '0' || ch > '9') ch = getchar();
	while (ch >= '0' && ch <= '9') {
		x = (x << 1) + (x << 3) + (ch ^ 48);
		ch = getchar();
	}
	return x;
}
const int N = 1e7 + 10;
int n, a[N];
int st[N], head;
int ls[N], rs[N]; 
signed main() {
	n = read(); 
	for (int i = 1; i <= n; i++) {
		a[i] = read();
	}
	for (int i = 1; i <= n; i++) {
		int k = head;
		while (k && a[st[k]] > a[i]) k--;
		if (k) rs[st[k]] = i;
		if (k < head) ls[i] = st[k + 1];
		st[++k] = i;
		head = k;
	}
	int ans1 = 0, ans2 = 0;
	for (int i = 1; i <= n; i++) {
		ans1 ^= i * (ls[i] + 1);
		ans2 ^= i * (rs[i] + 1);
	}
	printf("%lld %lld\n", ans1, ans2);
	
	return 0;
}

---

1. 二叉搜索树的性质是：左子结点的值比父亲小，右子节点的值比父亲大。 ↩︎

2. 堆的性质是：子节点比父亲大（小根堆）或比父亲小（大根堆）。 ↩︎