折半搜索（Meet in the Middle）

折半搜索（Meet in the Middle）

思想

先搜索前一半的状态，再搜索后一半的状态，再记录两边状态相结合的答案。

一般暴力搜索的时间复杂度是 \(O(2^n)\) 级别的，但是折半搜索可以将时间复杂度降到 \(O(2 \times 2^{\frac{n}{2}})\)。

例题

拿题说事儿。

P4799 [CEOI2015 Day2] 世界冰球锦标赛

[CEOI2015 Day2] 世界冰球锦标赛

题目描述

译自 CEOI2015 Day2 T1「Ice Hockey World Championship」

今年的世界冰球锦标赛在捷克举行。Bobek 已经抵达布拉格，他不是任何团队的粉丝，也没有时间观念。他只是单纯的想去看几场比赛。如果他有足够的钱，他会去看所有的比赛。不幸的是，他的财产十分有限，他决定把所有财产都用来买门票。

给出 Bobek 的预算和每场比赛的票价，试求：如果总票价不超过预算，他有多少种观赛方案。如果存在以其中一种方案观看某场比赛而另一种方案不观看，则认为这两种方案不同。

输入格式

第一行，两个正整数 \(N\) 和 \(M(1 \leq N \leq 40,1 \leq M \leq 10^{18})\)，表示比赛的个数和 Bobek 那家徒四壁的财产。

第二行，\(N\) 个以空格分隔的正整数，均不超过 \(10^{16}\)，代表每场比赛门票的价格。

输出格式

输出一行，表示方案的个数。由于 \(N\) 十分大，注意：答案 \(\le 2^{40}\)。

样例

样例输入

5 1000
100 1500 500 500 1000

样例输出

8

提示

样例解释

八种方案分别是：

• 一场都不看，溜了溜了
• 价格 \(100\) 的比赛
• 第一场价格 \(500\) 的比赛
• 第二场价格 \(500\) 的比赛
• 价格 \(100\) 的比赛和第一场价格 \(500\) 的比赛
• 价格 \(100\) 的比赛和第二场价格 \(500\) 的比赛
• 两场价格 \(500\) 的比赛
• 价格 \(1000\) 的比赛

有十组数据，每通过一组数据你可以获得 10 分。各组数据的数据范围如下表所示：

数据组号	\(1-2\)	\(3-4\)	\(5-7\)	\(8-10\)
\(N \leq\)	\(10\)	\(20\)	\(40\)	\(40\)
\(M \leq\)	\(10^6\)	\(10^{18}\)	\(10^6\)	\(10^{18}\)

思路

首先，这边有一个暴力代码。

#include <bits/stdc++.h>
#define int long long

using namespace std;

int read() {
	int x = 0; char ch = getchar();
	while (ch < '0' || ch > '9') ch = getchar();
	while (ch >= '0' && ch <= '9') {
		x = (x << 1) + (x << 3) + (ch ^ 48);
		ch = getchar();
	}
	return x;
}
const int N = 45;
int n, m, w[N];
int ans = 0;
void dfs(int now, int sum) {
	if (sum > m) return;
	if (now > n) {
		ans++;
		return;
	}
	dfs(now + 1, sum + w[now]);
	dfs(now + 1, sum);
}
signed main() {
	n = read(), m = read();
	for (int i = 1; i <= n; i++) {
		w[i] = read();
	}
	dfs(1, 0);
	printf("%lld\n", ans);
	
	return 0;
}

显然时间复杂度 \(O(2^n)\)，可以过掉 \(n \le 20\) 的点。

然而，如果我们使用折半搜索就可以将复杂度降至一半。我们将 \(n\) 分成两部分，前一部分从 \(1\) 搜索到 \(\frac{n}{2}\)，后一部分从 \(\frac{n}{2}+1\) 搜索到 \(n\)，以此让时间复杂度降到 \(O(2 \times 2^{\frac{n}{2}})\)。

我们将前一半的搜索状态存入 a 数组，将后一半的搜索状态存入 b 数组。接下来需要将两部分的答案组合统计。我们可以将 a 数组或 b 数组排序，然后通过枚举另一个数组中的状态，并在第一个数组中统计合法状态，进而统计答案。

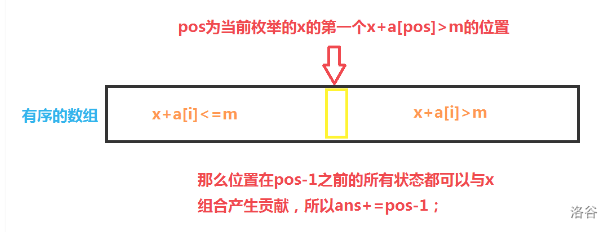
完整代码

#include <bits/stdc++.h>
#define int long long

using namespace std;

int read() {
	int x = 0; char ch = getchar();
	while (ch < '0' || ch > '9') ch = getchar();
	while (ch >= '0' && ch <= '9') {
		x = (x << 1) + (x << 3) + (ch ^ 48);
		ch = getchar();
	}
	return x;
}
const int N = 45, M = (1 << 20) + 5;
int n, m, w[N];
int ans = 0;
int suma[M], sumb[M], cnta, cntb; // 注意数组大小
void dfs(int l, int r, int sum, int a[], int &cnt) {
	if (sum > m) return;
	if (l > r) {
		a[++cnt] = sum;
		return;
	}
	dfs(l + 1, r, sum + w[l], a, cnt); // 选
	dfs(l + 1, r, sum, a, cnt);			// 不选
}
signed main() {
	n = read(), m = read();
	for (int i = 1; i <= n; i++) {
		w[i] = read();
	}
	int mid = n / 2; 
	dfs(1, mid, 0, suma, cnta);
	dfs(mid + 1, n, 0, sumb, cntb);
	sort(suma + 1, suma + 1 + cnta);
	for (int i = 1; i <= cntb; i++) {
		int pos = upper_bound(suma + 1, suma + 1 + cnta, m - sumb[i]) - suma;
		ans += (pos - 1);
	}
	printf("%lld\n", ans);
	
	return 0;
}

其他方面

也可以把前一半搜索的结果储存起来，在后一半搜索的时候直接结合前一半的结果统计答案。

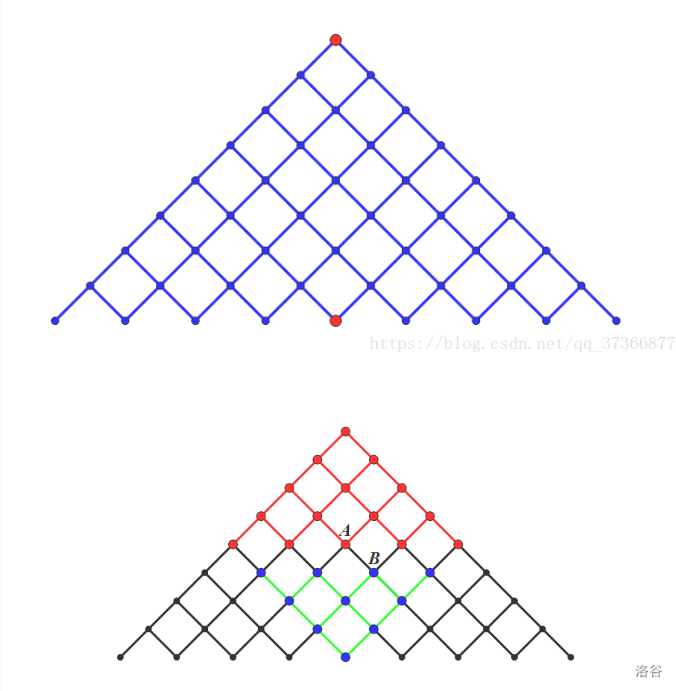
最后这边还有一张图可以拿来理解为什么折半搜索能优化复杂度。