二分图

二分图

概念

假设 \(G=(V,E)\) 是一个无向图，若点集 \(V\) 可以分解成互不相交的子集 \((A,B)\)，并且图中所有边 \((i,j)\) 的端点 \(i\)、\(j\) 分别属于子集 \(A\)、\(B\)，则称 \(G\) 是一个二分图。

判断

• 一张无向图时二分图，当且仅当图中不存在奇环。
• 如果某个图时二分图，那么他至少有两个顶点，且其所有回路长度均为偶数，任何无回路的图均是二分图（树就是二分图）。

染色法判定一个图是否是二分图

从其中一个点开始，将跟他连接的点染成与其不同的颜色，如果连接的点有颜色相同的，则说明不是二分图。

小知识：

匹配：无共同点的边的集合。

匹配数：边集中边的个数。

最大匹配：匹配数最大的匹配。

交错路：始于非匹配点且由匹配边与非匹配边交错而成。

增广路：始于非匹配点且终于非匹配点（除了起点的点）的交错路。

增广路性质：

• 增广路中的边的数量是奇数。

• 增广路上非匹配边比匹配边数量多 1。

• 奇数边是非匹配边，偶数边是匹配边。

• 如果将增广路上的匹配边和未匹配边反转，则匹配边数会增加 1。

最大匹配

概念

免了，上面说过了。

匈牙利算法

先说一句很玄的话：对于二分图最大匹配问题， \(M\) 为图 \(G\) 的最大匹配当且仅当找不到 \(M\) 的增广路。

用增广路求最大匹配，称作匈牙利算法。

本质：贪心。

具体步骤：

1. 该点时未匹配点：

   此时直接把两个点进行匹配。

2. 从与该节点匹配的左部分出发，可以找到另一个右部点与之匹配：

   此时递归进入该右部点的左部点，为其寻找匹配的右部点。

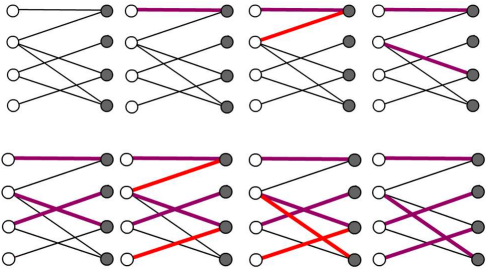
贴上这个：四个猛男和四个美女的故事

代码实现

// luogu P3386【模板】二分图最大匹配
#include <bits/stdc++.h>

using namespace std;

const int N = 505 + 10;
int n, m, e;		// 左部点数量，右部点数量，边数量
vector<int> G[N];	
int vis[N], pei[N];	// vis 记录右部点是否被访问，pei 记录每个右部点所匹配的点
bool dfs(int x) {
	for (int y : G[x]) {
		if (vis[y]) continue;
		vis[y] = 1;
		if (!pei[y] || dfs(pei[y])) {
            // 若所关联的点没被匹配或者 dfs 返回 true 说明可以与之匹配
			pei[y] = x;
			return true;
		}
	}
	return false;
}
int main() {
	scanf("%d%d%d", &n, &m, &e);
	for (int i = 1; i <= e; i++) {
		int x, y;
		scanf("%d%d", &x, &y);
		G[x].push_back(y);
	}
	int ans = 0;
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= m; j++) vis[j] = 0;
		if (dfs(i)) ans++;
	}
	printf("%d\n", ans);
	
	return 0;
}

最小点覆盖

概念

在一个图中任意选取最少的点，使得图中所有的边都与任意所选点相连。

定理

二分图最小点覆盖包含的点数等于二分图最大匹配包含的边数。

求解

那这张二分图举个例子。

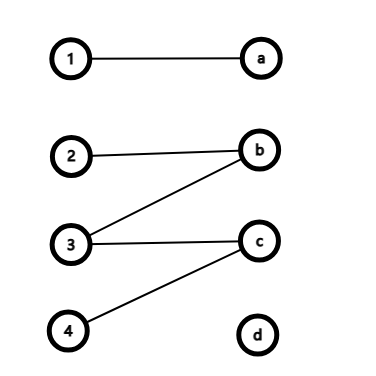
构造方法如下：

1. 求出最大匹配。假设该二分图的最大匹配是（1，a）、（2，b）、（3，c）。
2. 从左部点每个非匹配点出发，执行一次 dfs 找增广路的过程，标记所有访问过的节点。该二分图中从为匹配点 4 出发，走过的路径为 4 -> c -> 3 -> b -> 2。
3. 取左部点中没有打上标记的点和右部点中打上标记的点，得到最小点覆盖。该二分图取出 1、b、c 三个点，即为最小点覆盖点集。

证明：

在构造中，我们取左部点中没有被标记的点和右部点中被标记的点，则恰好是每条匹配边取了一个点，于是选出来的点数等于最大匹配的边数。

再来看这种取法是否能覆盖所有的边：

1. 显然匹配边一定被覆盖。
2. 显然不存在连接两个非匹配点的边。
3. 对于连接左部非匹配点和右部匹配点的边，后者必然被选，所以此边被覆盖。
4. 对于连接左部匹配点和右部非匹配点的边，那么前者必然未在步骤 2 的 dfs 中被标记，那么前者就必然被选，所以此边被覆盖。

最大独立集问题

概念

任意两点在图中都没有边相连的点集称为图的独立集。

选出最多的点构成独立集的点集大小即为最大独立集。

求解

二分图最大独立集 = 图的点数 - 二分图最大匹配

证明：

选出最多的点构成独立集，即在图中去掉最少的点使剩下的点之间没有边。用最少的点覆盖所有的边，去掉的边数即为最小点覆盖（二分图最小点覆盖 = 二分图最大匹配）。

最小路径覆盖问题

概念

在一个有向图中，找出最少的路径，使得这些路径经过了所有点即为路径覆盖。

最小路径覆盖又分为最小不相交路径覆盖和最小可相交路径覆盖。

求解

最小不相交路径覆盖

最小不相交路径覆盖：用尽量少的不相交简单路径覆盖有向无环图的所有点。

我们构造一张二分图。把原图中的每个点拆成二分图中左、右两个点：对于每条有向边 \((u,v)\)，从 \(u\) 的左部点向 \(v\) 的右部点连一条边。

则：最小路径覆盖 = 原图的点数 - 二分图最大匹配

证明：

首先，若最大匹配为 0，则二分图中没有边，说明原图中没有边。那么显然：

最小路径覆盖 = 原图的点数 - 0 = 原图的点数

若此时增加一条匹配边 \((x1, y2)\)，则在有向图中 \(x\)、\(y\) 在同一条路径上，最小路径覆盖数减少 1。

继续增加匹配边，每增加一条，最小路径数减少一个。

则：最小路径覆盖 = 原图的点数 - 二分图最大匹配 成立。

最小可相交路径覆盖

先用 floyd 求出原图的传递闭包，即如果 \(a\) 到 \(b\)，那么就加边 \((a,b)\)。然后就转化成了最小不相交路径覆盖问题。

证明：

意会。

二分图问题总结

基础二分图问题核心就是匈牙利算法。

1. 二分图的判定。（这个不用匈牙利算法）
2. 二分图最大匹配直接利用匈牙利算法求解。
3. 二分图最小点覆盖 = 最大匹配
4. 二分图最大独立集 = 总点数 - 最大匹配
5. 有向无环图最小路径覆盖 = 原图点数 - 构造二分图最大匹配