LCS算法和背包算法

1. 问题

LCS和背包算法，特别要求举例时采用不同于讲义的数据进行推导。

2. 解析

LCS：

由最长公共子序列问题的最优子结构性质可知，要找出X=<x1, x2, …, xm>和Y=<y1, y2, …, yn>的最长公共子序列，可按以下方式递归地进行：当xm=yn时，找出Xm-1和Yn-1的最长公共子序列，然后在其尾部加上xm(=yn)即可得X和Y的一个最长公共子序列。当xm≠yn时，必须解两个子问题，即找出Xm-1和Y的一个最长公共子序列及X和Yn-1的一个最长公共子序列。这两个公共子序列中较长者即为X和Y的一个最长公共子序列。

    由此递归结构容易看到最长公共子序列问题具有子问题重叠性质。例如，在计算X和Y的最长公共子序列时，可能要计算出X和Yn-1及Xm-1和Y的最长公共子序列。而这两个子问题都包含一个公共子问题，即计算Xm-1和Yn-1的最长公共子序列。

    与矩阵连乘积最优计算次序问题类似，我们来建立子问题的最优值的递归关系。用c[i,j]记录序列Xi和Yj的最长公共子序列的长度。其中Xi=<x1, x2, …, xi>，Yj=<y1, y2, …, yj>。当i=0或j=0时，空序列是Xi和Yj的最长公共子序列，故c[i,j]=0。其他情况下，由定理可建立递归关系如下：

 

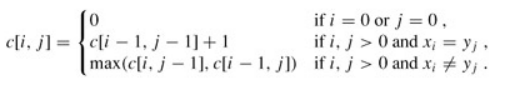
背包：

n=5是物品的数量，c=10是书包能承受的重量，w=[2,2,6,5,4]是每一个物品的重量，v=[6,3,5,4,6]是每一个物品的价值，先把递归的定义写出来：

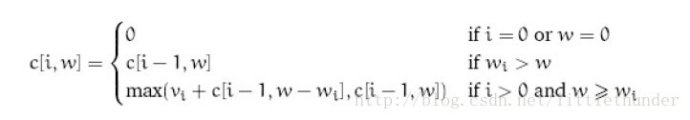
然后自底向上实现

3. 设计

LCS：

Procedure LCS(b,X,i,j);

begin

  if i=0 or j=0 then return;

  if b[i,j]="↖" then

    begin

      LCS(b,X,i-1,j-1);

      print(x[i]); {打印x[i]}

    end

  else if b[i,j]="↑" then LCS(b,X,i-1,j)

                      else LCS(b,X,i,j-1);

end;

 

背包：

for(int i=0;i<n;i++){

　　for(int j=m;j>=0;j--)

　　{

　　　　if(j>=w[i]){

　　　　dp[j]=max(dp[j],(dp[j-w[i]]+v[i]));

　　　　}

　　}

}

4. 分析

LCS：O(mn)

背包：O(N*W)

5. 源码

[github源码地址]