prim,kruskal算法求最小生成树
prim算法
1. 问题
假设无向图G,V为无向图顶点集合,E为无向图的边的集合。由V中的全部n个顶点和E中n-1条边构成的无向连通子图被称为G的一棵生成树,其中边的权值之和最小的生成树被称为无向图G的最小生成树。
2. 解析
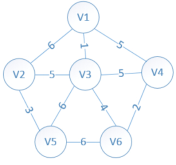
设置2个数组,
lowcost[i]:表示以i为终点的边的最小权值,当lowcost[i]=0说明以i为终点的边的最小权值=0,也 就是表示i点加入了MST
mst[i]:表示对应lowcost[i]的起点,即说明边<mst[i],i>是MST的一条边,当mst[i]=0表示起点i 加入MST,我们假设V1是起始点,进行初始化(*代表无限大,即无通路):
lowcost[2]=6,lowcost[3]=1,lowcost[4]=5,lowcost[5]=*,lowcost[6]=*
mst[2]=1,mst[3]=1,mst[4]=1,mst[5]=1,mst[6]=1,(所有点默认起点是V1)
明显看出,以V3为终点的边的权值最小=1,所以边<mst[3],3>=1加入MST,此时,因为点V3的加入, 需要更新lowcost数组和mst数组:
lowcost[2]=5,lowcost[3]=0,lowcost[4]=5,lowcost[5]=6,lowcost[6]=4
mst[2]=3,mst[3]=0,mst[4]=1,mst[5]=3,mst[6]=3
明显看出,以V6为终点的边的权值最小=4,所以边<mst[6],6>=4加入MST,此时,因为点V6的加入, 需要更新lowcost数组和mst数组:
lowcost[2]=5,lowcost[3]=0,lowcost[4]=2,lowcost[5]=6,lowcost[6]=0
mst[2]=3,mst[3]=0,mst[4]=6,mst[5]=3,mst[6]=0
明显看出,以V4为终点的边的权值最小=2,所以边<mst[4],4>=4加入MST,此时,因为点V4的加入, 需要更新lowcost数组和mst数组:
lowcost[2]=5,lowcost[3]=0,lowcost[4]=0,lowcost[5]=6,lowcost[6]=0
mst[2]=3,mst[3]=0,mst[4]=0,mst[5]=3,mst[6]=0
明显看出,以V2为终点的边的权值最小=5,所以边<mst[2],2>=5加入MST,此时,因为点V2的加入, 需要更新lowcost数组和mst数组:
lowcost[2]=0,lowcost[3]=0,lowcost[4]=0,lowcost[5]=3,lowcost[6]=0
mst[2]=0,mst[3]=0,mst[4]=0,mst[5]=2,mst[6]=0
很明显,以V5为终点的边的权值最小=3,所以边<mst[5],5>=3加入MST
lowcost[2]=0,lowcost[3]=0,lowcost[4]=0,lowcost[5]=0,lowcost[6]=0
mst[2]=0,mst[3]=0,mst[4]=0,mst[5]=0,mst[6]=0
至此,MST构建成功
3. 设计
prim{
for (i = 2; i <= n; i++)
{
lowcost[i] = 以i为终点的最小权值
mst[i] = 默认从v1出发
}
mst[1] = 0;
for (i = 2; i <= n; i++)
{
min = MAXCOST;
minid = 0;
for (j = 2; j <= n; j++)
{
/* 边权值较小且不在生成树中 */
if (lowcost[j] < min && lowcost[j] != 0)
{
min = lowcost[j];
minid = j;
}
}
printf("%c - %c : %d\n", mst[minid] + 'A' - 1, minid + 'A' - 1, min);
将min累加
lowcost[minid] = 0;
for (j = 2; j <= n; j++)
{
更新minmid到其他节点权值
}
}
return sum;
}
4. 分析
Prim算法的时间复杂度与网中的边数无关,适合于稠密图,时间复杂度O(n²),但可以用堆优化,优化后的Prim算法时间复杂度O(mlogn)。
5.[github源码地址]
Kruskal
1. 问题
假设无向图G,V为无向图顶点集合,E为无向图的边的集合。由V中的全部n个顶点和E中n-1条边构成的无向连通子图被称为G的一棵生成树,其中边的权值之和最小的生成树被称为无向图G的最小生成树。
2. 解析
首先,在初始状态下,对各顶点赋予不同的标记(用颜色区别),如下图所示:
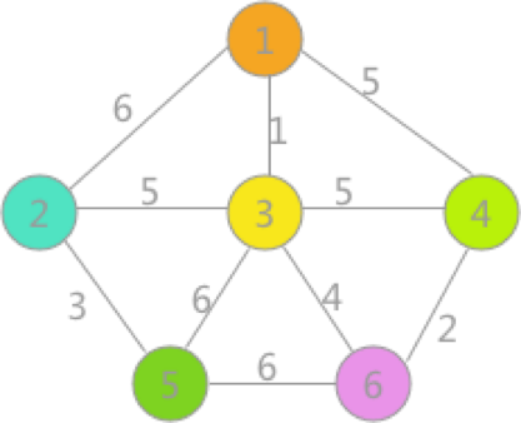
(1)
对所有边按照权值的大小进行排序,按照从小到大的顺序进行判断,首先是(1,3),由于顶点 1 和顶点 3 标记不同,所以可以构成生成树的一部分,遍历所有顶点,将与顶点 3 标记相同的全部更改为顶点 1 的标记,如(2)所示:
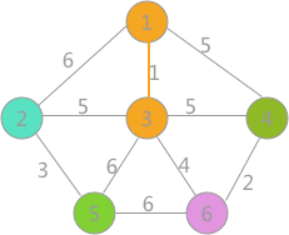
(2)
其次是(4,6)边,两顶点标记不同,所以可以构成生成树的一部分,更新所有顶点的标记为:
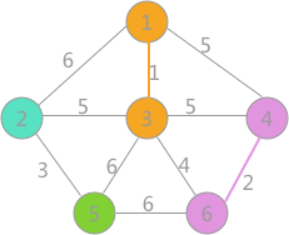
(3)
其次是(2,5)边,两顶点标记不同,可以构成生成树的一部分,更新所有顶点的标记为:
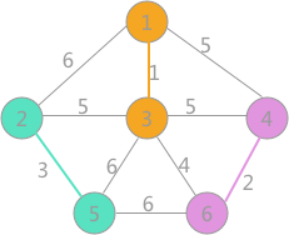
(4)
然后最小的是(3,6)边,两者标记不同,可以连接,遍历所有顶点,将与顶点 6 标记相同的所有顶点的标记更改为顶点 1 的标记:
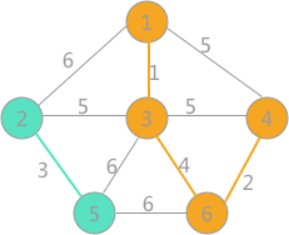
(5)
继续选择权值最小的边,此时会发现,权值为 5 的边有 3 个,其中(1,4)和(3,4)各自两顶点的标记一样,如果连接会产生回路,所以舍去,而(2,3)标记不一样,可以选择,将所有与顶点 2 标记相同的顶点的标记全部改为同顶点 3 相同的标记:
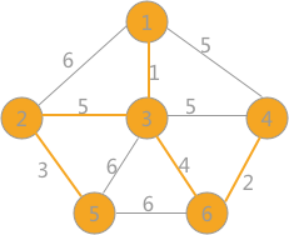
(6)
当选取的边的数量相比与顶点的数量小 1 时,说明最小生成树已经生成。所以最终采用克鲁斯卡尔算法得到的最小生成树为(6)所示。
3. 设计
A=∅
For each vertex v ∈G,V
Make-set(v)
Sort the edges of G,E into nondecreasing order by weight w
For each edge(u,v)∈G,E, taken in nondecresing order by weight
If find-set(u)≠find-set(v)
A=AU{(u,v)}
Union(u,v)
Return A
1、初始化生成树的边集A为空集
2、对集合中的每一个顶点,都将它的集合初始化为自身
3、将边按权值进行排序
4、对排序好后的边从小到大进行判断:如果这条边所连的2个顶点不在同一个集合中,则将这条边加入到生成树的边集A中,并将此边所连的两个顶点u和v的集合做一个Union操作,如此循环加到生成树中的边集数量为n-1时停止
4.分析
初始化生成树的边集A为空集:O(1)
对集合中的每一个顶点,都将它的集合初始化为自身:O(V)
将边按权值进行排序:O(ElogE)
对排序好后的边从小到大进行判断,如果这条边所连的2个顶点不在同一个集合中,则将这条边加入到生成树的边集A中,并将此边所连的两个顶点u和v的集合做一个Union操作,如此循环加到生成树中的边集数量为n-1时停止由于各个子块不是嵌套的而是顺序的,所以时间复杂度取最高的那个即为O(ElogE)
5.源码


 浙公网安备 33010602011771号
浙公网安备 33010602011771号