多项式回归
多项式回归简介
考虑下面即将出现的数据,虽然我们可以使用线性回归来拟合这些数据,但是这些数据更像是一条二次曲线,相应的方程是 $y=ax^{2}+bx+c$ ,这是式子虽然可以理解为二次方程,但是我们呢可以从另外一个角度来理解这个式子:
如果将 $x^{2}$ 理解为一个特征,将 $x$ 理解为另外一个特征,换句话说,本来我们的样本只有一个特征 $x$ ,现在我们把他看成有两个特征的一个数据集。多了一个特征 $x^{2}$ ,那么从这个角度来看, 这个式子依旧是一个线性回归的式子,但是从 $x$ 的角度来看,它就是一个二次的方程。
以上这样的方式,就是所谓的多项式回归相当于我们为样本多添加了一些特征,这些特征是原来样本的多项式项,增加了这些特征之后,我们可以使用线性回归的思路来更好的处理我们的数据。
什么是多项式回归
数据来源
import numpy as np import matplotlib.pyplot as plt # 生成100个数字 1*100 np.random.seed(100) x = np.random.uniform(-3, 3, size=100) # 100*1 X = x.reshape(-1, 1) # 一元二次方程 y = 0.5 * x**2 + x + 2 + np.random.normal(0, 1, 100) plt.scatter(x, y) plt.show()
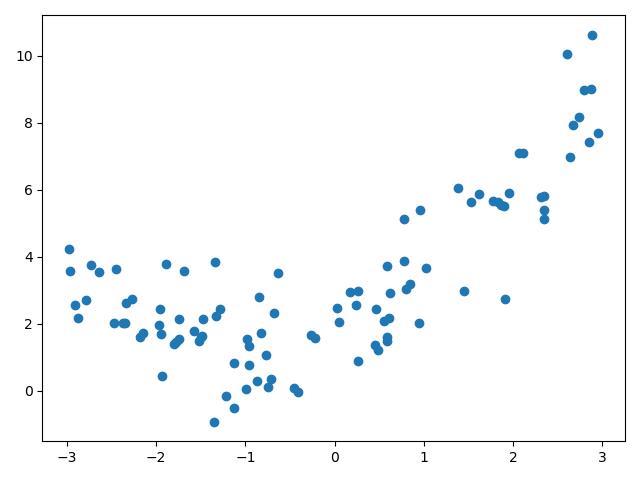
线性回归拟合
# 线性回归线 from sklearn.linear_model import LinearRegression lin_reg = LinearRegression() lin_reg.fit(X, y) y_predict = lin_reg.predict(X) plt.scatter(x, y) plt.plot(x, y_predict, color='r') plt.show()
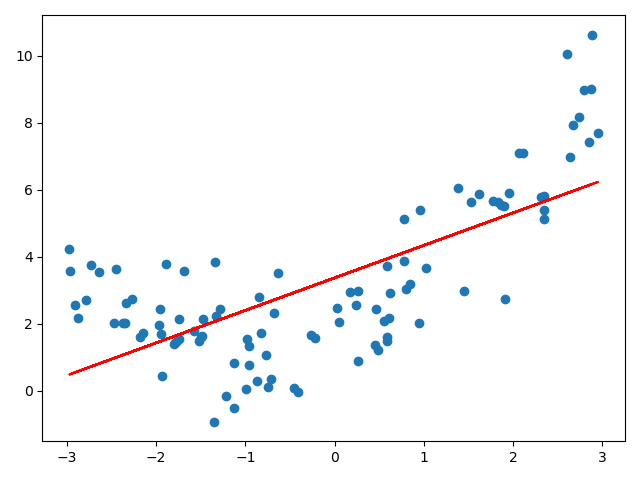
很明显,我们用一跟直线来拟合一根有弧度的曲线,效果是不好的
解决 :添加一个特征
# 原来所有的数据都在X中,现在对X中每一个数据都进行平方, 再将得到的数据集与原数据集进行拼接, 在用新的数据集进行线性回归 from sklearn.linear_model import LinearRegression lin_reg2 = LinearRegression() lin_reg2.fit(X2, y) X2 = np.hstack([X, X**2]) y_predict2 = lin_reg2.predict(X2) plt.scatter(x, y) # 由于x是乱的,所以应该进行排序 plt.plot(np.sort(x), y_predict2[np.argsort(x)], color='r') plt.show()
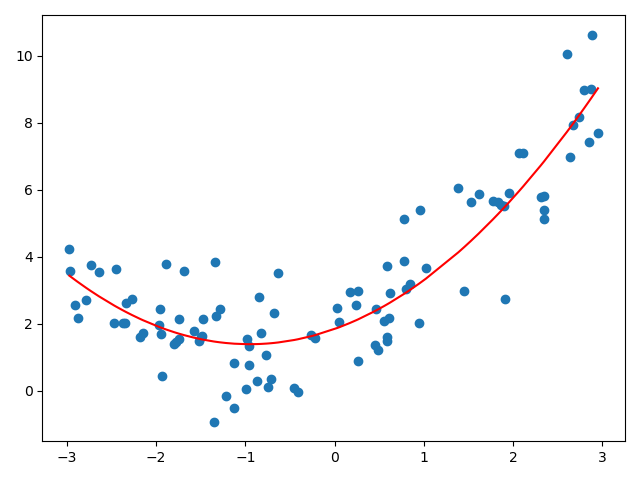
从上图可以看出,当我们添加了一个特征(原来特征的平方)之后,再从x的维度来看,就形成了 一条曲线,显然这个曲线对原来数据集的拟合程度是更好的
# 查看x的系数 # 第一个系数是x前面的系数,第二个系数是x平方前面的系数 lin_reg2.coef_ # [0.95406518 0.50130709] # 查看常数 lin_reg2.intercept_ # 1.8432063555039913
即该模型拟合的曲线为 $y=0.95406518x^{2}+ 0.50130709x+1.8432063555039913$
总结
多线性回归在机器学习算法上并没有新的地方,完全是使用线性回归的思路。他的关键在于 为原来的样本,添加新的特征。而我们得到新的特征的方式是原有特征的多项式的组合。 采用这 样的方式,我们就可以解决一些非线性的问题
与此同时需要主要,我们在上一章所讲的PCA是对我们的数据进行降维处理,而我们这一章所讲 的多项式回归显然在做一件相反的事情,他让我们的数据升维,在升维之后使得我们的算法可以更 好的拟合高纬度的数据
scikit-learn中的多项式回归和Pipeline
导入数据
import numpy as np import matplotlib.pyplot as plt x = np.random.uniform(-3, 3, size=100) X = x.reshape(-1, 1) # X.shape --> (100, 1) y = 0.5 * x**2 + x + 2 + np.random.normal(0, 1, 100) # sklearn中对数据进行预处理的函数都封装在preprocessing模块下,包括之前学的归一化StandardScal er from sklearn.preprocessing import PolynomialFeatures # 最高次数2次 poly = PolynomialFeatures(degree=2) poly.fit(X) X2 = poly.transform(X) # X2.shape --> (100, 3)
查看差别
print(X[:5, :]) """ [[-1.55352926] [ 1.53422389] [-2.57530034] [ 1.30115235] [-1.34130485]] """ print(X2[:5, :]) # 第一列是sklearn为我们添加的X^0的特征 # 第二列和原来的特征一样是X^1的特征 # 第三列是添加的X^2的特征 """ [[ 1. -1.55352926 2.41345318] [ 1. 1.53422389 2.35384294] [ 1. -2.57530034 6.63217186] [ 1. 1.30115235 1.69299744] [ 1. -1.34130485 1.7990987 ]] """
绘制图形
from sklearn.linear_model import LinearRegression lin_reg2 = LinearRegression() lin_reg2.fit(X2, y) y_predict2 = lin_reg2.predict(X2) plt.scatter(x, y) plt.plot(np.sort(x), y_predict2[np.argsort(x)], color='r') plt.show()
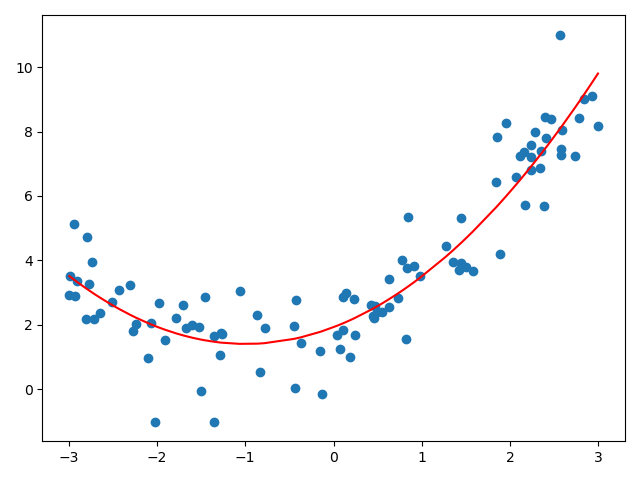
结果
print(lin_reg2.coef_) # [0. 0.95218822 0.48750701] print(lin_reg2.intercept_) # 2.0472357913665844
关于PolynomialFeatures
import numpy as np from sklearn.preprocessing import PolynomialFeatures X = np.arange(1, 11).reshape(-1, 2) """ X.shape --> (5, 2) [[ 1 2] [ 3 4] [ 5 6] [ 7 8] [ 9 10]] """ poly = PolynomialFeatures(degree=2) poly.fit(X) X2 = poly.transform(X) """ X2.shape --> (5, 6) [[ 1. 1. 2. 1. 2. 4.] [ 1. 3. 4. 9. 12. 16.] [ 1. 5. 6. 25. 30. 36.] [ 1. 7. 8. 49. 56. 64.] [ 1. 9. 10. 81. 90. 100.]] """
我们可以看到,将5行2列的矩阵进行多项式转换后变成了5行6列
- 第一列是1 对应的是0次幂
- 第二列和第三列对应的是原来的x矩阵,此时他有两列一次幂的项
- 第四列是原来数据的第一列平方的结果
- 第六列是原来数据的第二列平方的结果
- 第五列是原来数据的两 列相乘的结果
可以想象如果将degree设置为3,那么将产生一下10个元素,即
$1,x_{1},x_{2},
x_{1}^{2},x_{2}^{2},x_{1}x_{2},
x_{1}^{3},x_{2}^{3},x_{1}^{2}x_{2},x_{1}x_{2}^{2},
\cdots$
也就是说PolynomialFeatures会穷举出所有的多项式组合
Pipeline
pipline的英文名字是管道,那么我们如何使用管道呢,先考虑我们多项式回归的过程
- 1.使用PolynomialFeatures生成多项式特征的数据集
- 2.如果生成数据幂特别的大,那么特征直接的 差距就会很大,导致我们的搜索非常慢,这时候可以进行数据归一化
- 3.进行线性回归
pipline 的作用就是把上面的三个步骤合并,使得我们不用一直重复这三步
import numpy as np import matplotlib.pyplot as plt from sklearn.linear_model import LinearRegression x = np.random.uniform(-3, 3, size=100) X = x.reshape(-1, 1) y = 0.5 * x**2 + x + 2 + np.random.normal(0, 1, 100) from sklearn.pipeline import Pipeline from sklearn.preprocessing import StandardScaler, PolynomialFeatures # 传入每一步的对象名和类的实例化 poly_reg = Pipeline([ ("poly", PolynomialFeatures(degree=2)), ("std_scaler", StandardScaler()), ("lin_reg", LinearRegression()) ]) poly_reg.fit(X, y) y_predict = poly_reg.predict(X) plt.scatter(x, y) plt.plot(np.sort(x), y_predict[np.argsort(x)], color='r') plt.show()

过拟合和欠拟合
欠拟合
算法所训练的模型不能完整表述数据关系
过拟合
算法所训练的模型过多的表达了数据间的噪音关系
一、线性回归
数据来源
import numpy as np import matplotlib.pyplot as plt np.random.seed(666) x = np.random.uniform(-3.0, 3.0, size=100) X = x.reshape(-1, 1) y = 0.5 * x**2 + x + 2 + np.random.normal(0, 1, size=100) plt.scatter(x, y, c='b') plt.show()
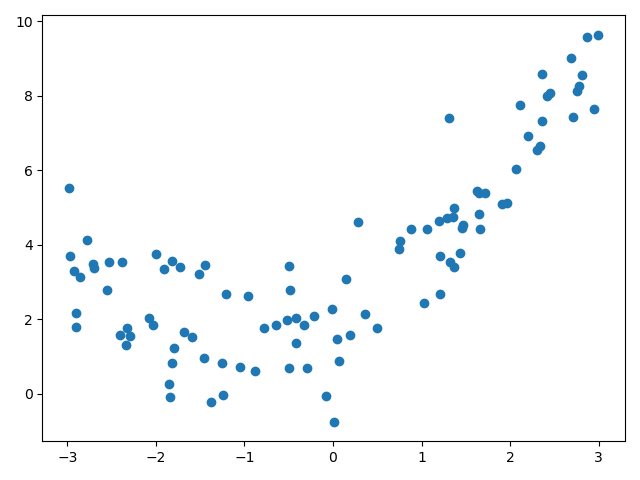
使用线性回归
from sklearn.linear_model import LinearRegression lin_reg = LinearRegression() lin_reg.fit(X, y) y_predict = lin_reg.predict(X) plt.scatter(x, y) plt.plot(np.sort(x), y_predict[np.argsort(x)], color='r') plt.show()
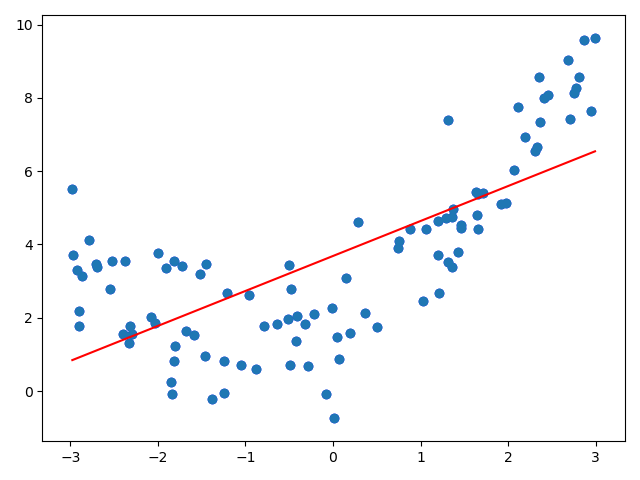
查看评分和均方误差
使用均方误差来看拟合的结果,这是因为我们同样都是对一组数据进行拟合,所以使用不同的方法对数据进行拟合 得到的均方误差的指标是具有可比性的。
print(lin_reg.score(X, y)) # 0.4953707811865009 from sklearn.metrics import mean_squared_error y_predict = lin_reg.predict(X) print(mean_squared_error(y, y_predict)) # 3.0750025765636577
二、多项式回归
使用多项式回归
import numpy as np import matplotlib.pyplot as plt from sklearn.metrics import mean_squared_error from sklearn.linear_model import LinearRegression from sklearn.pipeline import Pipeline from sklearn.preprocessing import PolynomialFeatures from sklearn.preprocessing import StandardScaler np.random.seed(666) x = np.random.uniform(-3.0, 3.0, size=100) X = x.reshape(-1, 1) y = 0.5 * x**2 + x + 2 + np.random.normal(0, 1, size=100) def PolynomialRegression(degree): return Pipeline([ ("poly", PolynomialFeatures(degree=degree)), ("std_scaler", StandardScaler()), ("lin_reg", LinearRegression()) ])
$n=2$
poly2_reg = PolynomialRegression(degree=2) # 查看管道 poly2_reg.fit(X, y) y2_predict = poly2_reg.predict(X) plt.scatter(x, y) plt.plot(np.sort(x), y2_predict[np.argsort(x)], color='r') plt.show() print(mean_squared_error(y, y2_predict)) # 1.0987392142417858 print(poly2_reg.score(X, y)) # 0.819689285599819
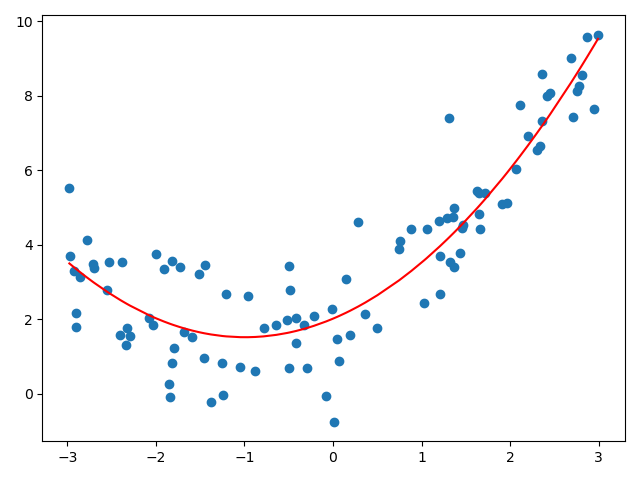
$n=10$
poly10_reg = PolynomialRegression(degree=10) # 查看管道 poly10_reg .fit(X, y) y10_predict = poly10_reg .predict(X) plt.scatter(x, y) plt.plot(np.sort(x), y10_predict [np.argsort(x)], color='r') plt.show() print(mean_squared_error(y, y10_predict )) # 1.0508466763764126 print(poly10_reg.score(X, y)) # 0.8275487827443734
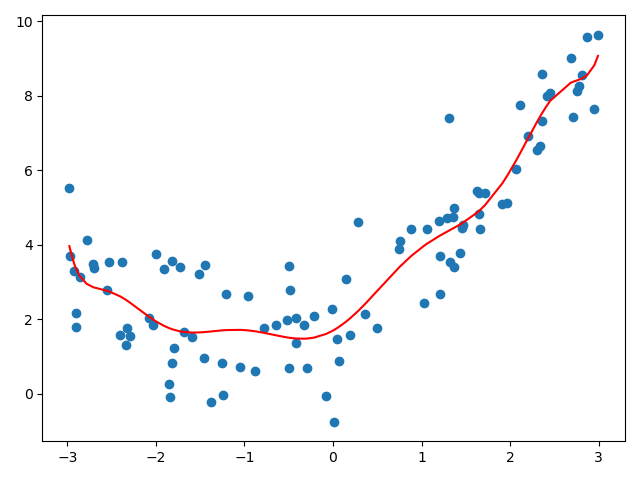
$n=100$
poly100_reg = PolynomialRegression(degree=100) # 查看管道 poly100_reg .fit(X, y) y100_predict = poly100_reg .predict(X) plt.scatter(x, y) plt.plot(np.sort(x), y100_predict [np.argsort(x)], color='r') plt.show() print(mean_squared_error(y, y100_predict )) # 0.6839223451864704 print(poly100_reg.score(X, y)) # 0.8877636066353388
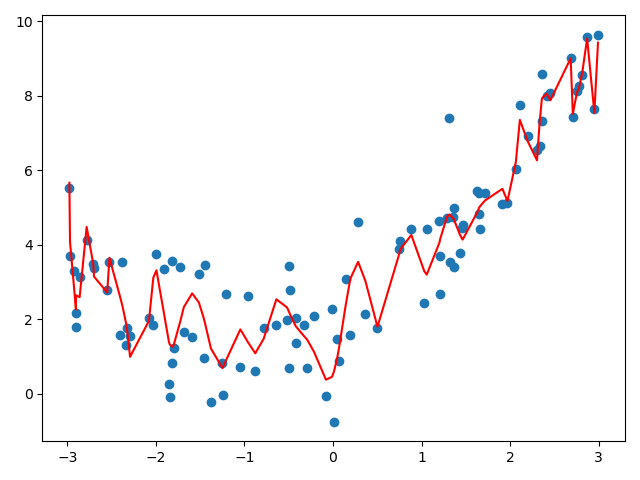
这条曲线只是原来随机生成的点(分布不均匀)对应的y的预测值连接起来的曲线,不过有x轴很多地方可能没有数据点,所以连接的结果和原来的曲线不一样(不是真实的y曲线)。 下面尝试真正还原原来的曲线(构造均匀分布的原数据集)
poly100_reg = PolynomialRegression(degree=100) poly100_reg .fit(X, y) X_plot = np.linspace(-3, 3, 100).reshape(100, 1) y_plot = poly100_reg.predict(X_plot) plt.scatter(x, y) plt.plot(X_plot[:,0], y_plot, color='r') plt.axis([-3, 3, 0, 10]) plt.show() print(poly100_reg.score(X, y)) # 0.8877636066353388
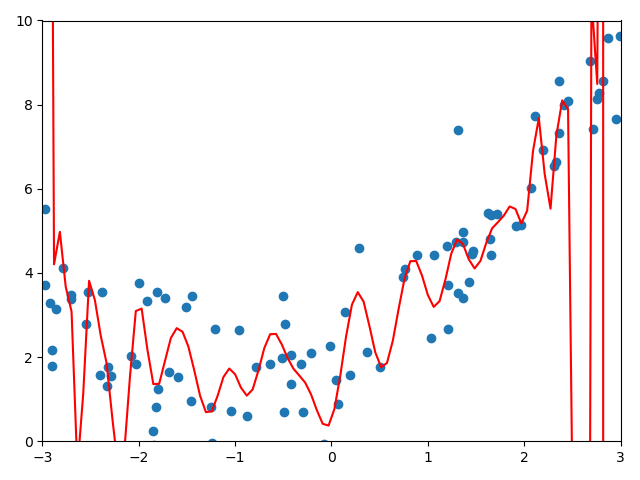
总结
- 总有一条曲线,他能拟合所有的样本点,使得均方误差的值为0
- degree从2到10到100的过程中,虽然均方误差是越来越小的,从均方误差的角度来看是更加小的 但是他真的能更好的预测我们数据的走势吗,例如我们选择2.5到3的一个x,使用上图预测出来的y的大小(0或者-1之间)显然不符合我们的数据
- 换句话说,我们使用了一个非常高维的数据,虽然使得我们的样本点获得了更小的误差,但是这根曲线完全不是我们想要的样子 他为了拟合我们所有的样本点,变的太过复杂了,这种情况就是过拟合【over-fitting】
- 相反,在最开始,我们直接使用一根直线来拟合我们的数据,也没有很好的拟合我们的样本特征,当然他犯的错误不是太过复杂了,而是太过简单了 这种情况,我们成为欠拟合【under-fitting】
对于现在的数据(基于二次方程构造),我们使用低于2项的拟合结果,就是欠拟合;高于2项的拟合结果,就是过拟合
为什么要使用训练数据集和测试数据集
模型的泛化能力
使用上图的过拟合结果,我们可以得知,虽然我们训练出的曲线将原来的样本点拟合的非常好,总体的误差非常的小, 但是一旦来了新的样本点,他就不能很好的预测了,在这种情况下,我们就称我们得到的这条弯弯曲曲的曲线,他的泛化能力(由此及彼的能力)非常弱
训练数据集和测试数据集的意义
- 模型目的是为了使得预测的数据能够尽肯能的准确
- 观察训练数据集的拟合程度是没有意义的
- 需要模型的泛化能力更高
解决这个问题的方法也就是使用训练数据集,测试数据集的分离
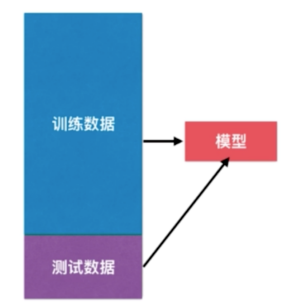
测试数据对于我们的模型是全新的数据,如果使用训练数据获得的模型面对测试数据也能获 得很好的结果,那么我们就说我们的模型泛化能力是很强的。 如果我们的模型面对测试数据结果很差的话,那么他的泛化能力就很弱。事实上,这是训练数据集更大的意义
划分测试集与训练集
from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=666)
$n=1$
lin_reg = LinearRegression() lin_reg.fit(X_train, y_train) y_predict = lin_reg.predict(X_test) mean_squared_error(y_test, y_predict) # 2.2199965269396573
$n=2$
poly2_reg = PolynomialRegression(degree=2) poly2_reg.fit(X_train, y_train) y2_predict = poly2_reg.predict(X_test) mean_squared_error(y_test, y2_predict) # 0.80356410562978997
$n=10$
poly10_reg = PolynomialRegression(degree=10) poly10_reg.fit(X_train, y_train) y10_predict = poly10_reg.predict(X_test) mean_squared_error(y_test, y10_predict) # 0.92129307221507939
$n=100$
poly100_reg = PolynomialRegression(degree=100) poly100_reg.fit(X_train, y_train) y100_predict = poly100_reg.predict(X_test) mean_squared_error(y_test, y100_predict) # 14075796419.234262
总结
刚刚我们进行的实验实际上在实验模型的复杂度
- 对于多项式模型来说,我们回归的阶数越高,我们的模型会越复杂
- 对于KNN来说,是K越小,模型越复杂,k越大,模型最简单
-
- 当k=n的时候,模型就简化成了看整个样本里,哪种样本最多
- 当k=1来说,对于每一个点,都要找到离他最近的那个点
- 横轴是模型复杂度
- 纵轴是模型准确率(也就是他能够多好的预测我们的曲线)
| 算法 | 系数 | 分析 |
| KNN | K值 | K越小,复杂度越高 |
| 多项式回归 | 阶数 | 阶数越高,复杂度越高 |
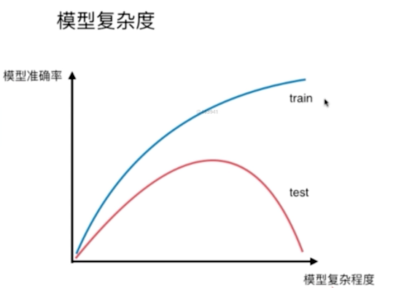
通常对于这样一个图,会有两根曲线:
- 一个是对于训练数据集来说的,模型越复杂,模型准确率越高,因为模型越复杂,对训练数据集的拟合就越好,相应的模型准确率就越高
- 对于测试数据集来说,在模型很简单的时候,模型的准确率也比较低,随着模型逐渐变复杂,对测试数据集的准确率在逐渐的提升,提升到一定程度后,如果模型继续变复杂,那么我们的模型准确率将会进行下降(欠拟合->正合适->过拟合)
学习曲线
线性回归
import numpy as np import matplotlib.pyplot as plt np.random.seed(666) x = np.random.uniform(-3.0, 3.0, size=100) X = x.reshape(-1, 1) y = 0.5 * x**2 + x + 2 + np.random.normal(0, 1, size=100) # 实现学习曲线 from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=10) # print(X_train.shape) # (75,1) # 观察线性回归的学习曲线:观察线性回归模型,随着训练数据集增加,性能的变化 from sklearn.linear_model import LinearRegression from sklearn.metrics import mean_squared_error train_score = [] test_score = [] for i in range(1, 76): lin_reg = LinearRegression() lin_reg.fit(X_train[:i], y_train[:i]) y_train_predict = lin_reg.predict(X_train[:i]) train_score.append(mean_squared_error(y_train[:i], y_train_predict)) y_test_predict = lin_reg.predict(X_test) test_score.append(mean_squared_error(y_test, y_test_predict)) plt.plot([i for i in range(1, 76)], np.sqrt(train_score), label="train") plt.plot([i for i in range(1, 76)], np.sqrt(test_score), label="test") plt.legend() plt.show()
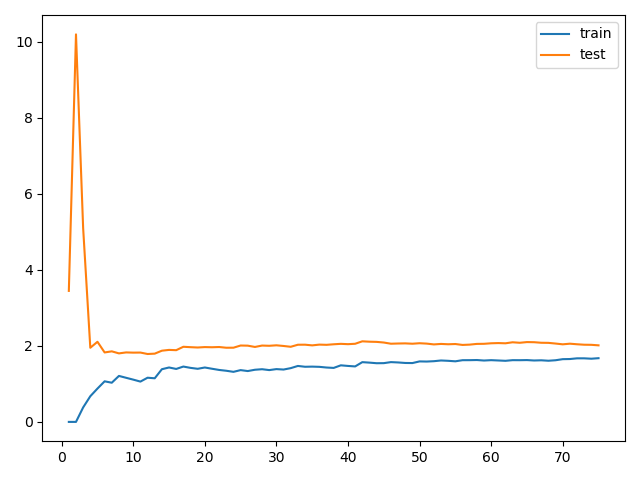
- 在训练数据集上,误差是逐渐升高的。这是因为我们的训练数据越来越多,我们的数据点越难得到全部的累积,不过整体而言,在刚开始的时候误差变化的比较快,后来就几乎不变了
- 在测试数据集上,在使用非常少的样本进行训练的时候,刚开始我们的测试误差非常的大,当训练样本大到一定程度以后,我们的测试误差就会逐渐减小,减小到一定程度后,也不会小太多,达到一种相对稳定的情况
- 在最终,测试误差和训练误差趋于相等,不过测试误差还是高于训练误差一些,这是因为,训练数据在数据非常多的情况下,可以将数据拟合的比较好,误差小一些,但是泛化到测试数据集的时候,还是有可能多一些误差
线性回归的学习曲线封装
def plot_learning_curve(algo, X_train, X_test, y_train, y_test): train_score = [] test_score = [] for i in range(1, len(X_train)+1): algo.fit(X_train[:i], y_train[:i]) y_train_predict = algo.predict(X_train[:i]) train_score.append(mean_squared_error(y_train[:i], y_train_predict)) y_test_predict = algo.predict(X_test) test_score.append(mean_squared_error(y_test, y_test_predict)) plt.plot([i for i in range(1, len(X_train)+1)], np.sqrt(train_score), label="train") plt.plot([i for i in range(1, len(X_train)+1)], np.sqrt(test_score), label="test") plt.legend() plt.axis([0, len(X_train)+1, 0, 4]) plt.show() plot_learning_curve(LinearRegression(), X_train, X_test, y_train, y_test)
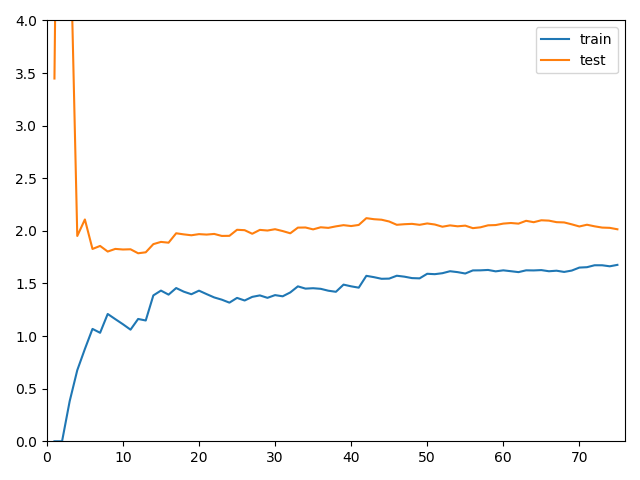
多项式回归
$n=2$
from sklearn.preprocessing import PolynomialFeatures from sklearn.preprocessing import StandardScaler from sklearn.pipeline import Pipeline def PolynomialRegression(degree): return Pipeline([ ("poly", PolynomialFeatures(degree=degree)), ("std_scaler", StandardScaler()), ("lin_reg", LinearRegression()) ]) poly2_reg = PolynomialRegression(degree=2) plot_learning_curve(poly2_reg, X_train, X_test, y_train, y_test)
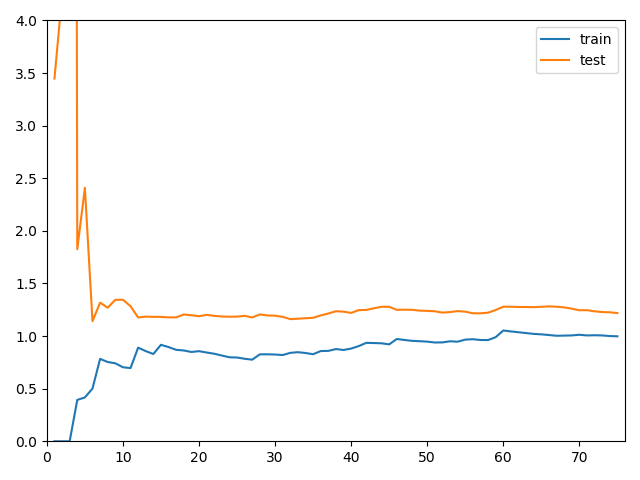
- 整体从趋势上,和线性回归的学习曲线是类似的
- 线性回归的学习曲线1.5,1.8左右
- 2阶多项式回归稳定在了1.0,0.9左右
- 2阶多项式稳定的误差比较低,说明使用二阶线性回归的性能是比较好的
$n=20$
poly20_reg = PolynomialRegression(degree=20)
plot_learning_curve(poly20_reg, X_train, X_test, y_train, y_test)
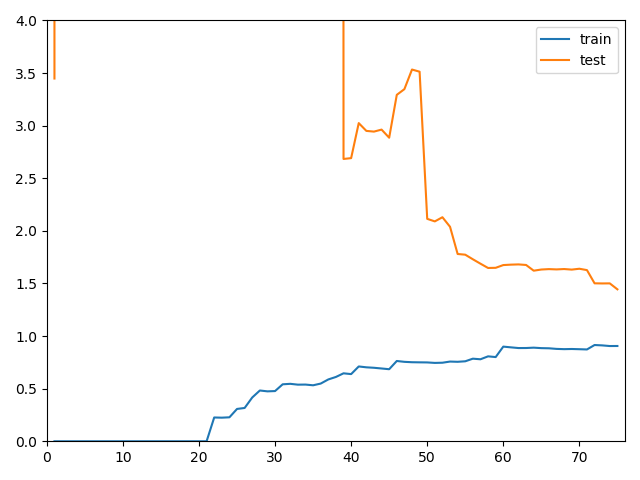
在使用20阶多项式回归训练模型的时候可以发现,在数据量偏多的时候,我们的训练数据集拟合的是比较好的,但是测试数据集的误差相对来说增大了很多,离训练数据集比较远,通常这就是过拟合的结果,他的泛化能力是不够的
总结
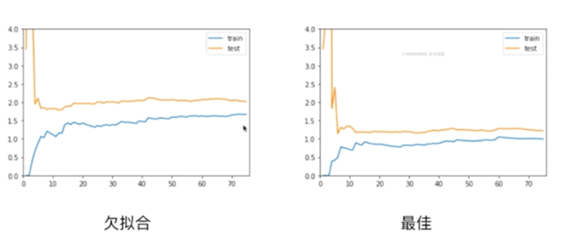
对于欠拟合比最佳的情况趋于稳定的那个位置要高一些,说明无论对于训练数据集还是测试数据集来说,误差都比较大。这是因为我们本身模型选的就不对,所以即使在训练数据集上,他的误差也是大的,所以才会呈现出这样的一种形态
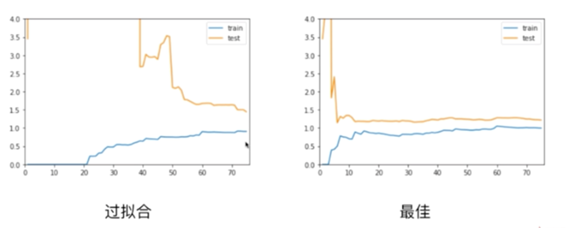
对于过拟合的情况,在训练数据集上,他的误差不大,和最佳的情况是差不多的,甚至在极端情况,如果degree取更高的话,那么训练数据集的误差会更低,但是问题在于,测试数据集的误差相对是比较大的,并且训练数据集的误差和测试数据集的误差相差比较大(表现在图上相差比较远),这就说明了此时我们的模型的泛化能力不够好,他的泛化能力是不够的
验证数据集与交叉验证


 浙公网安备 33010602011771号
浙公网安备 33010602011771号