算法笔记_链表

链表

单链表结构

// 单链表节点的结构
public class ListNode {
    int val;
    ListNode next;
    ListNode(int x) { val = x; }
}

反转链表的一部分，就是给定一个索引区间，把单链表的中的这部分元素反转，其他部分保持不变。

递归反转链表

1、递归反转整个链表

ListNode reverse(ListNode head) {
      //base case
      if(head.next == null) {
            return head;
      }
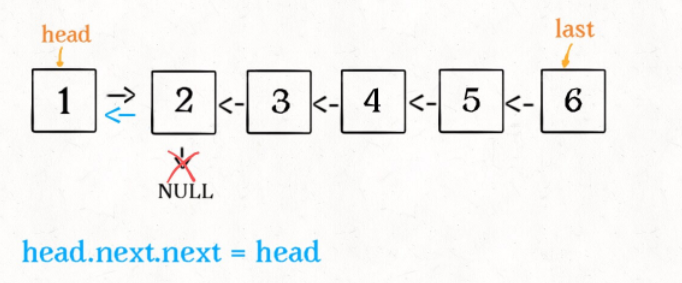
      ListNode last = reverse(head.next);
      //反转子链表
      head.next.next = head;
      head.next = null;
      //返回子问题链表头节点
      return last;
}

head.next.next = head

2、反转链表的前N个节点

// 将链表的前 n 个节点反转（n <= 链表长度）
ListNode reverseN(ListNode head, int n)

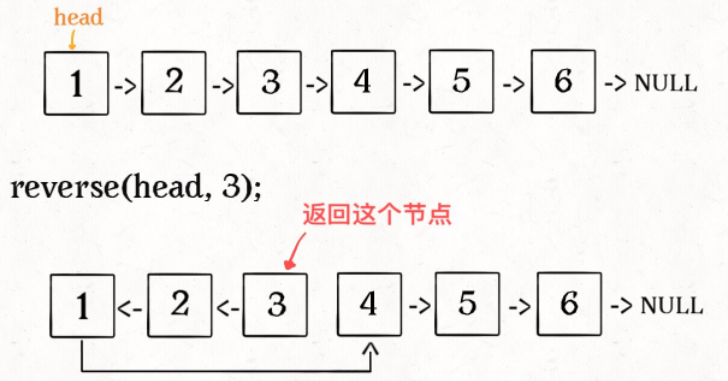
跟上述反转整个链表形式差不多，增加一个后驱节点用来记住反转链表的下一个节点，base case 设置为 n == 1

//后继节点
ListNode successor = null;

ListNode reverse(ListNode head, int n) {
      //base case
      if(n == 1) {
            //记录第 n+1 个节点
            successor = head.next;
            return head;
      }
      //以 head.next 为起点，反转前 n - 1 个节点
      ListNode last = reverse(head.next, n-1);
      //反转子链表
      head.next.next = head;
      head.next = successor;
      //返回子问题链表头节点
      return last;
}

3、反转部分链表

给一个索引区间 [m,n]（索引从 1 开始），仅仅反转区间中的链表元素。

ListNode reverseBetween(ListNode head, int m, int n)

主要思路：前进到反转的起点，触发反转的base case

ListNode reverseBetween(ListNode head, int m, int n) {
      //base case
      if(m == 1) {
            return reverse(head, n);
      }
      //前进到第m个节点，触发base case
      head.next = reverseBetween(head.next, m-1, n-1);
      return head;
}
ListNode reverse(ListNode head, int n) {
      //base case
      if(n == 1) {
            //记录第 n+1 个节点
            successor = head.next;
            return head;
      }
      //以 head.next 为起点，反转前 n - 1 个节点
      ListNode last = reverse(head.next, n-1);
      //反转子链表
      head.next.next = head;
      head.next = successor;
      //返回子问题链表头节点
      return last;
}

时间复杂度O(N)，空间复杂度O(N)

---

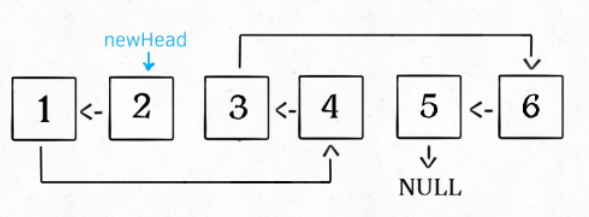
k个元素一组反转链表

首先是反转节点a到节点b之间[a，b)的节点，左闭右开

ListNode reverse(ListNode a, ListNode b) {
      ListNode pre, cur, nxt;
      pre = null;
      cur = nxt = a;
      while(cur != b) {
            nxt = cur.next;
            cur.next = pre;
            pre = cur;
            cur = nxt;
      }
      //返回反转后的头节点
      return pre;
}

上述方法迭代实现了反转部分链表的作用，下面编写reverseKGroup函数具体代码

ListNode reverseKGroup(ListNode head, int k) {
      if(head == null) return null;
      //区间[a,b)包含k个待反转的元素
      ListNode a, b;
      a = b = head;
      for (int i = 0; i < k; i++) {
            if(b == null) return head;
            b = b.next;
      }
      //反转前k个元素
      ListNode newHead = reverse(a,b);
      a.next = reverseKGroup(b, k);
      return newHead;
}

判断回文链表

1、利用递归函数的堆栈解法

// 左侧指针
ListNode left;

boolean isPalindrome(ListNode head) {
    left = head;
    return traverse(head);
}

boolean traverse(ListNode right) {
    if (right == null) return true;
    boolean res = traverse(right.next);
    // 后序遍历代码
    res = res && (right.val == left.val);
    left = left.next;
    return res;
}

时间复杂度O(N)、空间复杂度O(N)

2、优化空间复杂度

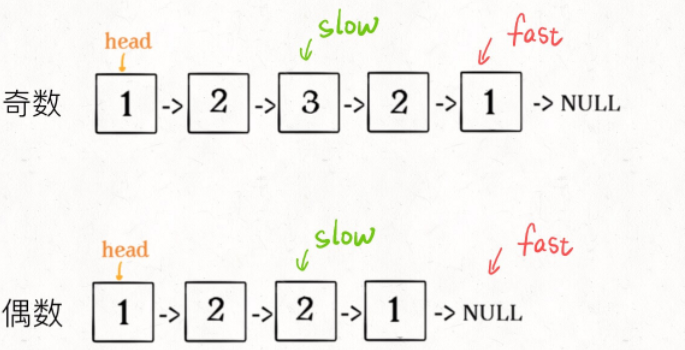
1、先通过「双指针技巧」中的快慢指针来找到链表的中点：

ListNode slow, fast;
slow = fast = head;
while (fast != null && fast.next != null) {
    slow = slow.next;
    fast = fast.next.next;
}
// slow 指针现在指向链表中点

2、如果fast指针没有指向null，说明链表长度为奇数，slow还要再前进一步：

if (fast != null)
    slow = slow.next;

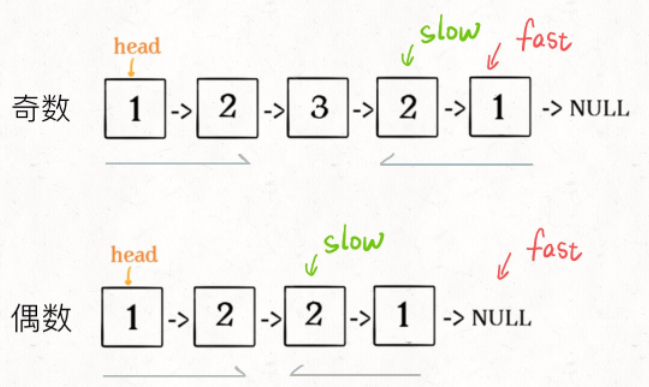
3、从slow开始反转后面的链表，现在就可以开始比较回文串了：

ListNode left = head;
ListNode right = reverse(slow);

while (right != null) {
    if (left.val != right.val)
        return false;
    left = left.next;
    right = right.next;
}
return true;

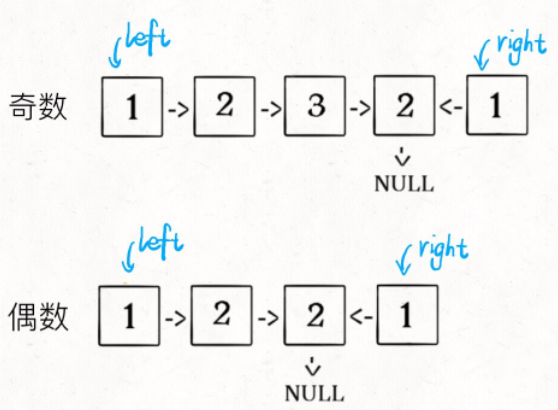
将上述3段代码合在一起即可

public boolean isPalindrome(ListNode head) {
        ListNode slow, fast;
        slow = fast = head;
        while(fast != null && fast.next !=null) {
            slow = slow.next;
            fast = fast.next.next;
        }
        if(fast != null) {
            slow = slow.next;
        }
        ListNode left = head;
        ListNode right = reverse(slow);
        while(right != null) {
            if(left.val != right.val) {
                return false;
            }
            left = left.next;
            right = right.next;
        }
        return true;
    }
    public ListNode reverse(ListNode head) {
        if(head == null) {
            return null;
        }
        ListNode pre, cur, nxt;
        pre = null;
        cur = nxt = head;
        while(cur != null) {
            nxt = cur.next;
            cur.next = pre;
            pre = cur;
            cur = nxt;
        }
        return pre;
    }

算法总体的时间复杂度 O(N)，空间复杂度 O(1)
寻找回文串是从中间向两端扩展，判断回文串是从两端向中间收缩。对于单链表，无法直接倒序遍历，可以造一条新的反转链表，可以利用链表的后序遍历，也可以用栈结构倒序处理单链表。

文字参考自：https://labuladong.gitee.io/algo/