图-拓扑排序+练习题

前言：图-拓扑排序的学习和实现笔记

参考文章：https://www.jianshu.com/p/b59db381561a

有向无环图(DAG）

在学习拓扑排序之前，先了解一个概念有向无环图（DAG）

有向无环图DAG的定义：有向无环图指的是一个无回路的有向图。

如果有一个非有向无环图，且A点出发向B经C可回到A，形成一个环。

将从C到A的边方向改为从A到C，则变成有向无环图，比如下面这张图的话那么就是一张有向无环图

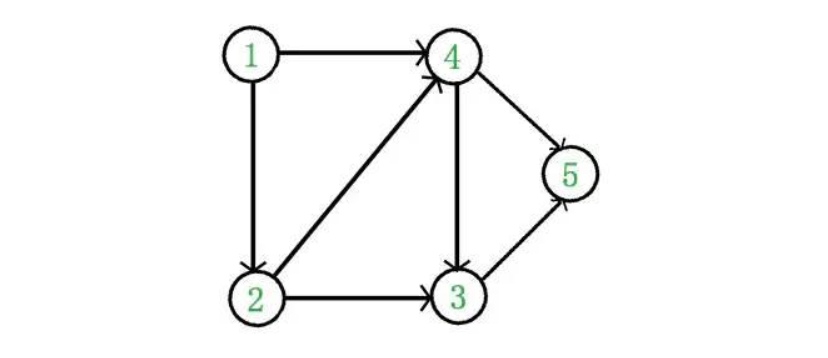
如果是下面这种多了一条4->1的边长的话，那么类似下面这种的话就是非DAG图，也就是非有向无环图

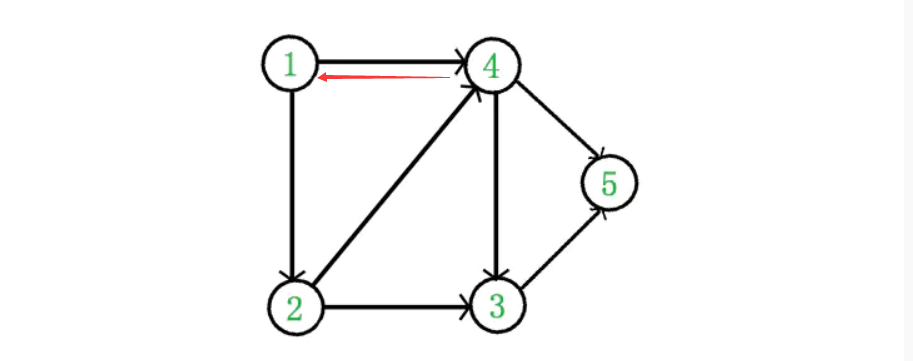
知识点：有向无环图（DAG）才有拓扑排序，非DAG图没有拓扑排序一说。

什么是AOV网

它的全称是Activity On Vertex NetWork，用顶点表示的活动的网

而在AOV网中，都是用DAG图（有向无环图）表示一个工程。

其中的顶点表示活动，有向边<Vi,Vj>表示活动Vi必须先于活动Vj进行，如下图所示，这种就是一个AOV网表示的一个工程

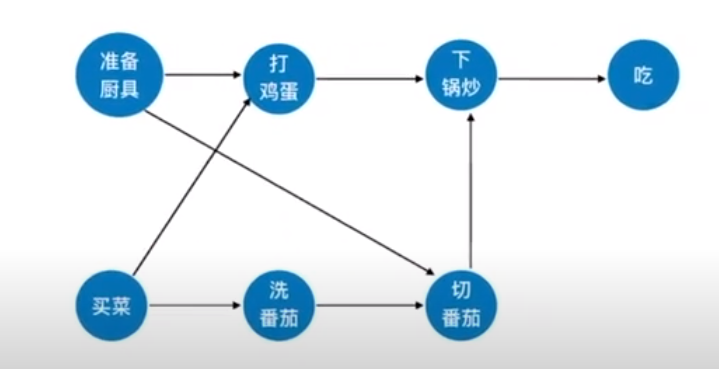
这里举个例子如下所示，类似这种的话在AOV网中，其中构成了一个环路，那么就不能称之为一个AOV网

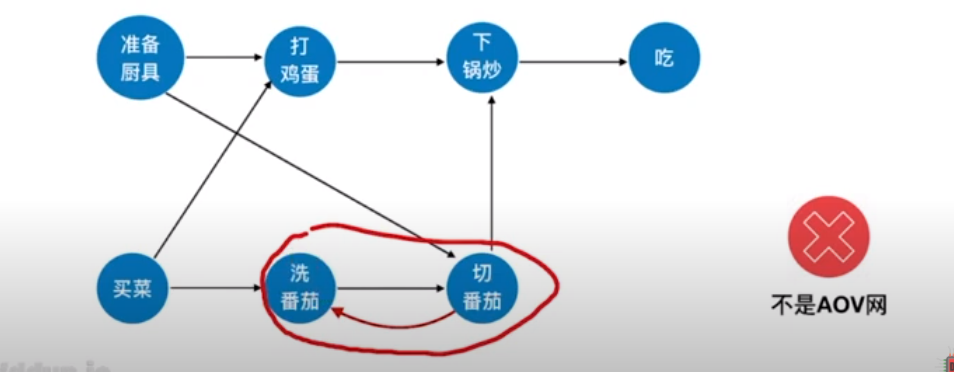
什么是拓扑排序

总结下拓扑排序的作用，简而言之其实就是判断一个有向图是否是无环图，但是在AOV网中通过拓扑排序，我们可以实现排序工程中的每个顶点之间的活动顺序，上面的例子经过排序过后就如下所示

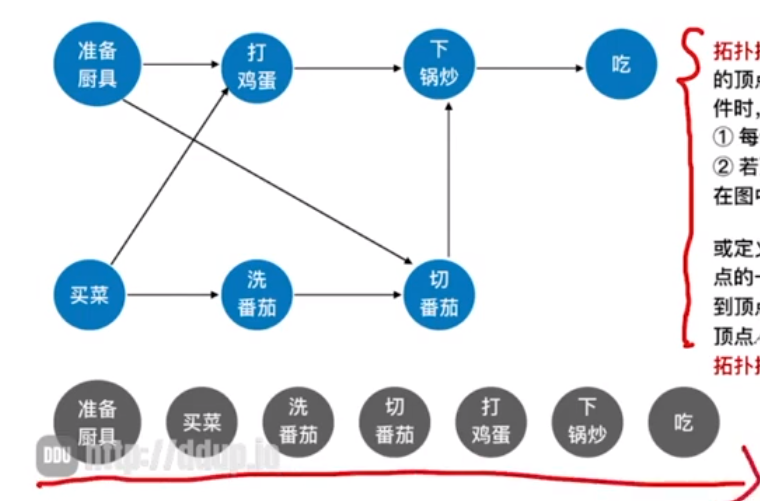
在图论中，拓扑排序（Topological Sorting）是一个有向无环图（DAG，Directed Acyclic Graph）的所有顶点的线性序列。

且该序列必须满足下面两个条件：

• 每个顶点出现且只出现一次。

• 若存在一条从顶点 A 到顶点 B 的路径，那么在序列中顶点 A 出现在顶点 B 的前面。

如何手动写出有向无环图的拓扑排序

一个知识点：通常，一个有向无环图可以有一个或多个拓扑排序序列。

• 从 DAG 图中选择一个 没有前驱（即入度为0）的顶点并输出。

• 从图中删除该顶点和所有以它为起点的有向边。

• 重复 1 和 2 直到当前的 DAG 图为空或当前图中不存在无前驱的顶点为止。后一种情况说明有向图中必然存在环。

代码实现有向无环图的拓扑排序

#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#define OK 1
#define ERROR 0
#define MAX 32767
typedef int Status;

typedef struct _Graph
{
	int vexNum;	// 顶点数量
	int arcNum;	// 边长数量
	int** arcs;		// 边长的0或者1，大小就是arcsNum*arcsNum
	char* vexs;		// 顶点的名称
}Graph, *PGraph;

// 图的初始化
Graph* initGraph(int vexNum)
{
	Graph* pGraph = NULL;
	if (pGraph == NULL)
	{
		pGraph = (Graph*)malloc(sizeof(Graph));
		memset(pGraph, 0, sizeof(Graph));
		if (pGraph == NULL)
			return NULL;
		pGraph->vexNum = vexNum; // 顶点的数量
		pGraph->vexs = (char*)malloc(sizeof(pGraph->vexNum));
		memset(pGraph->vexs, 0, sizeof(pGraph->vexNum));
		pGraph->arcNum = 0; // 初始化为0，因为到时候craeteGraph的时候完了之后再进行最终边数的计算
		pGraph->arcs = (int**)malloc(sizeof(int*)* pGraph->vexNum);
		memset(pGraph->arcs, sizeof(int*)* pGraph->vexNum, 0);
		// 一个图中每个顶点都有对应的n个顶点的边数
		for (int i = 0; i < pGraph->vexNum; i++)
		{
			pGraph->arcs[i] = malloc(sizeof(int)* pGraph->vexNum);
			memset(pGraph->arcs[i], 0, sizeof(int)*pGraph->vexNum);
		}
	}
	return pGraph;
}

// 顶点和边之间的关系初始化
Status createGraph(Graph** pGraph, char* vexs, int* arcs)
{
	if (*pGraph == NULL)
		return ERROR;
	for (int i = 0; i<(*pGraph)->vexNum; i++)
	{
		*((*pGraph)->vexs + i) = *(vexs + i);
		for (int j = 0; j<(*pGraph)->vexNum; j++)
		{
			(*pGraph)->arcs[i][j] = *(arcs + i*((*pGraph)->vexNum) + j);
			printf("%d ", (*pGraph)->arcs[i][j]);
			if ((*pGraph)->arcs[i][j] == 1)
				(*pGraph)->arcNum++;
		}
		printf("\n");
	}
	// 无向图的边数还需要除以2
	(*pGraph)->arcNum /= 2;
	return OK;
}

// 深度优先遍历
Status DFS(Graph* pGraph, int* iVisitedArray, int visitedIndex)
{
	if (pGraph == NULL)
		return ERROR;
	iVisitedArray[visitedIndex] = 1;
	printf("%c ", pGraph->vexs[visitedIndex]);
	for (int i = 0; i<pGraph->vexNum; i++)
	{
		if (pGraph->arcs[visitedIndex][i] == 1 && !iVisitedArray[i])
			DFS(pGraph, iVisitedArray, i);
	}
	return OK;
}

void getTopoSort(Graph* pGraph)
{
	int iFlag; // 标识符
	int visitedArray[5] = { 0 };
	for (int m = 0;m<pGraph->vexNum;m++)
	{
		for (int i = 0; i < pGraph->vexNum; i++)
		{
			iFlag = 1;
			if (!visitedArray[i])
			{
				for (int j = 0; j < pGraph->vexNum; j++)
				{
					if (pGraph->arcs[j][i] != 0 && pGraph->arcs[j][i] != MAX)
					{
						iFlag = 0; break;
					}
				}
				if (iFlag)
				{
					for (int k = 0; k < pGraph->vexNum; k++){ if (pGraph->arcs[i][k] == 1)pGraph->arcs[i][k]--; }
					printf("输出顶点%c\n", pGraph->vexs[i]);
					visitedArray[i] = 1;
					break;
				}
			}
		}
	}
}

int main()
{
	// 要初始化的矩阵
	int visited[5] = { 0 };
	int initArcs[5][5] =
	{
		0,1,MAX,1,MAX,
		MAX,0,1,1,MAX,
		MAX,MAX,0,MAX,1,
		MAX,MAX,1,0,1,
		MAX,MAX,MAX,MAX,0
	};
	char initVexs[6] = "12345";
	Graph* pGraph = initGraph(5); // 要初始化的顶点的数量
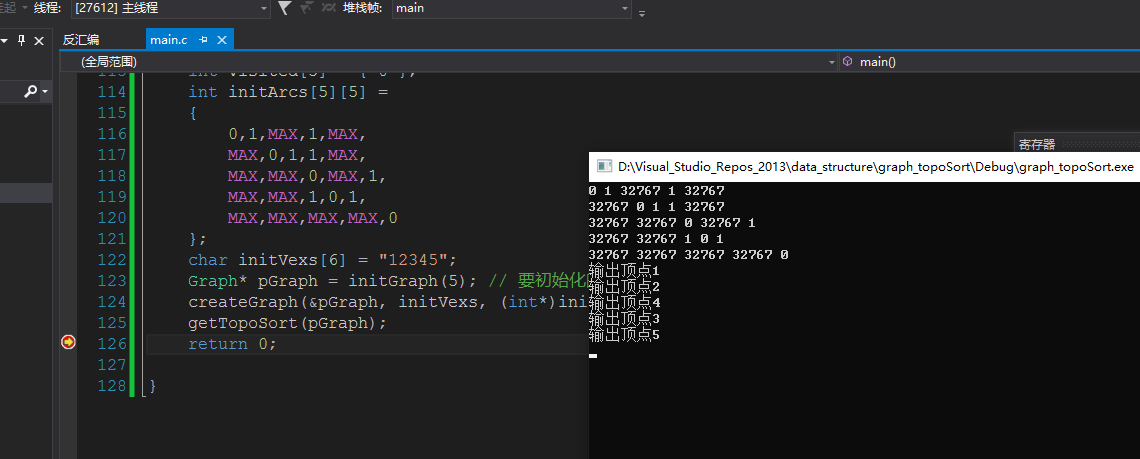
	createGraph(&pGraph, initVexs, (int*)initArcs);
	getTopoSort(pGraph);
	return 0;
	
}

练习题

问题描述：有一串数字1到5，按照下面的关于顺序的要求，重新排列并打印出来。要求如下：2在5前出现，3在2前出现，4在1前出现，1在3前出现。

看到题目就知道是进行构造相关的无环图dag，那么这里可以通过dfs或者bfs来进行实现，我这里的话就通过dfs来进行实现，go代码如下

思路就是先构造对应的主键的map，然后通过遍历map来进行判断是否能够构造出对应的完整连续的dag来，可以的话则成功

package main

import (
	"fmt"
)

// 问题描述：有一串数字1到5，按照下面的关于顺序的要求，重新排列并打印出来。要求如下：2在5前出现，3在2前出现，4在1前出现，1在3前出现

var gmap2 map[string]string = map[string]string{
	"2": "5",
	"3": "2",
	"4": "1",
	"1": "3",
}

//反转数组顺序
func reverse(arr []string) {
	for i, j := 0, len(arr)-1; i < j; i, j = i+1, j-1 {
		arr[i], arr[j] = arr[j], arr[i]
	}
}

var q []string
var visited_ map[string]bool

func tapo_sort3(k string) {
	if !visited_[k] {
		visited_[k] = true
		q = append(q, k)
		if gmap2[gmap2[k]] != "" {
			q = append(q, gmap2[k])
			tapo_sort3(gmap2[gmap2[k]])
		}
	}
}

func main() {
	for k, _ := range gmap2 {
		fmt.Printf("\t %s\n", k)
		q = make([]string, 0)
		visited_ = make(map[string]bool, 0)
		tapo_sort3(k)
		// reverse(q)
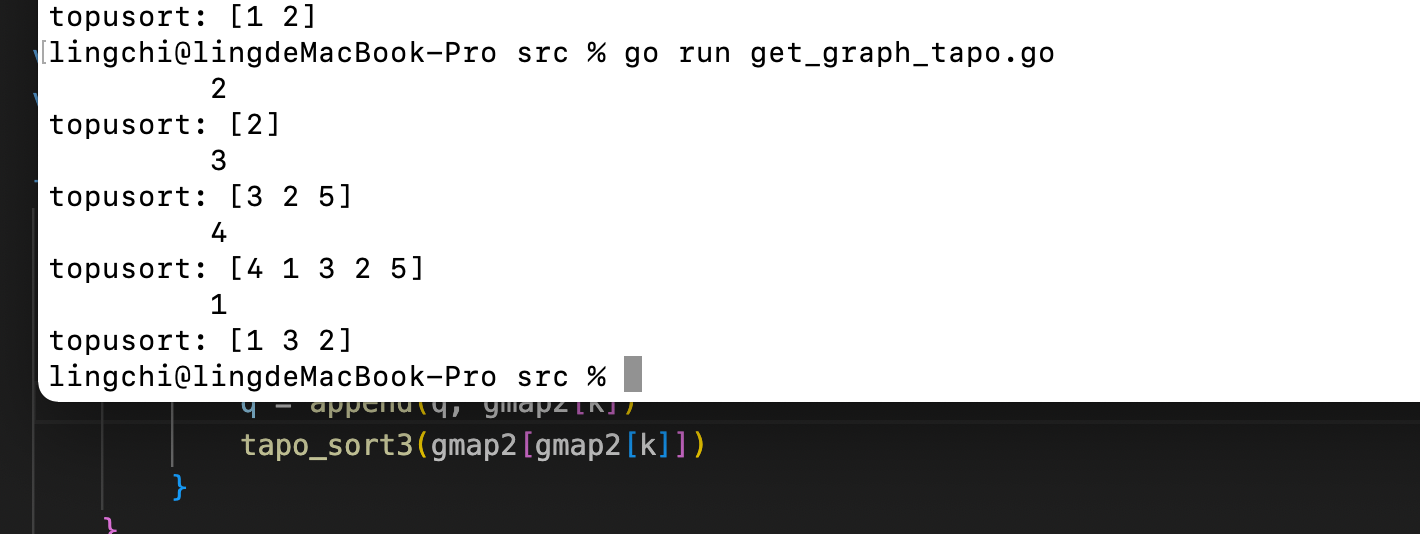
		fmt.Printf("topusort: %v \n", q)
	}

}