图的邻接矩阵创建和深度优先遍历DFS和广度优先遍历BFS

前言：图的创建和深度优先遍历DFS和广度优先遍历BFS

图的邻接矩阵创建

// 图的初始化
Graph* initGraph(int vexNum)
{
	Graph* pGraph = NULL;
	if (pGraph == NULL)
	{
		pGraph = (Graph*)malloc(sizeof(Graph));
		memset(pGraph, 0, sizeof(Graph));
		if (pGraph == NULL)
			return NULL;
		pGraph->vexNum = vexNum; // 顶点的数量
		pGraph->vexs = (char*)malloc(sizeof(pGraph->vexNum));
		memset(pGraph->vexs, 0, sizeof(pGraph->vexNum));
		pGraph->arcNum = 0; // 初始化为0，因为到时候craeteGraph的时候完了之后再进行最终边数的计算
		pGraph->arcs = (int**)malloc(sizeof(int*)* pGraph->vexNum);
		memset(pGraph->arcs, sizeof(int*)* pGraph->vexNum, 0);
		// 一个图中每个顶点都有对应的n个顶点的边数
		for (int i = 0; i < pGraph->vexNum; i++)
		{
			pGraph->arcs[i] = malloc(sizeof(int)* pGraph->vexNum);
			memset(pGraph->arcs[i], 0, sizeof(int)*pGraph->vexNum);
		}
	}
	return pGraph;
}
 
// 顶点和边之间的关系初始化
Status createGraph(Graph** pGraph, char* vexs, int* arcs)
{
	if (*pGraph == NULL)
		return ERROR;
	for (int i = 0; i<(*pGraph)->vexNum; i++)
	{
		*((*pGraph)->vexs + i) = *(vexs + i);
		for (int j = 0; j<(*pGraph)->vexNum; j++)
		{
			(*pGraph)->arcs[i][j] = *(arcs + i*((*pGraph)->vexNum) + j);
			printf("%d ", (*pGraph)->arcs[i][j]);
			if ((*pGraph)->arcs[i][j] == 1)
				(*pGraph)->arcNum++;
		}
		printf("\n");
	}
	// 无向图的边数还需要除以2
	(*pGraph)->arcNum /= 2;
	return OK;
}

深度优先遍历DFS

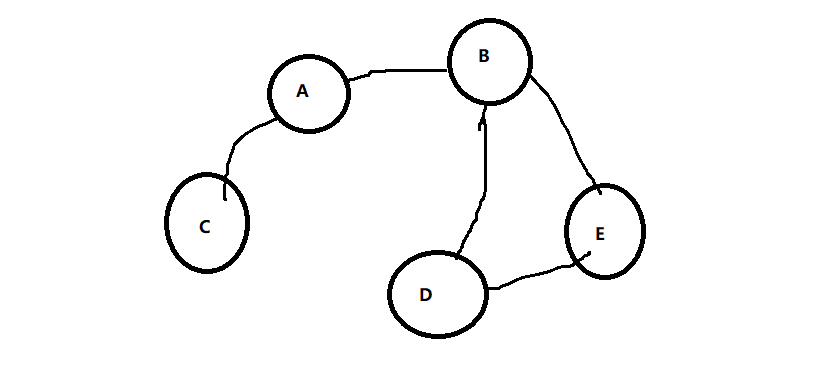
其实很好理解的，就是从一个点开始，就比如我有ABCDE五个点，然后该无向图的路径为如下所示

• 如果我是从A出发的话，那么我就可以走到C或者B这两点，这里的话这两个点都是可以走，我这里选B点好了
• 然后到了B点之后，A已经访问过了，所以还可以走D和E，走到了D，那么就还有E这个点
• 到了E之后都走不了了，那么只能回去A，最后再访问C即可
• 这里的"深度"可以理解为能走就一直走，不能走再绕路走

那么写代码就很简单了，通过一个标识符的数组和递归的方式即可解决

// 深度优先遍历
Status DFS(Graph* pGraph, int* iVisitedArray, int visitedIndex)
{
	if (pGraph == NULL)
		return ERROR;
	iVisitedArray[visitedIndex] = 1;
	printf("%c ", pGraph->vexs[visitedIndex]);
	for (int i = 0; i<pGraph->vexNum; i++)
	{
		//printf("%d ", pGraph->arcs[visitedIndex][j]);
		if (pGraph->arcs[visitedIndex][i] == 1 && !iVisitedArray[i])
			DFS(pGraph, iVisitedArray, i);
	}
	return OK;
}
 
int main()
{
	// 要初始化的矩阵
	int visited[5] = { 0 };
	int initArcs[5][5] =
	{
		0, 1, 1, 0, 0,
		1, 0, 1, 1, 1,
		1, 1, 0, 0, 0,
		0, 1, 0, 0, 0,
		0, 1, 0, 1, 0 
        };
	char initVexs[6] = "ABCDE";
	Graph* pGraph = initGraph(5); // 要初始化的顶点的数量
	createGraph(&pGraph, initVexs, (int*)initArcs);
	DFS(pGraph, visited, 0);
	return 0;
}
 

广度优先遍历BFS

• 跟树的层序遍历是一样的，通过一个队列来进行存储，然后遍历所有的顶点与顶点之间的边，通过标识符来进行认别是否已经访问过

• 每次访问一个顶点都将其放入到队列中，在下次遍历的时候将其弹出进行遍历

• 如上两个操作即可实现广度优先遍历BFS

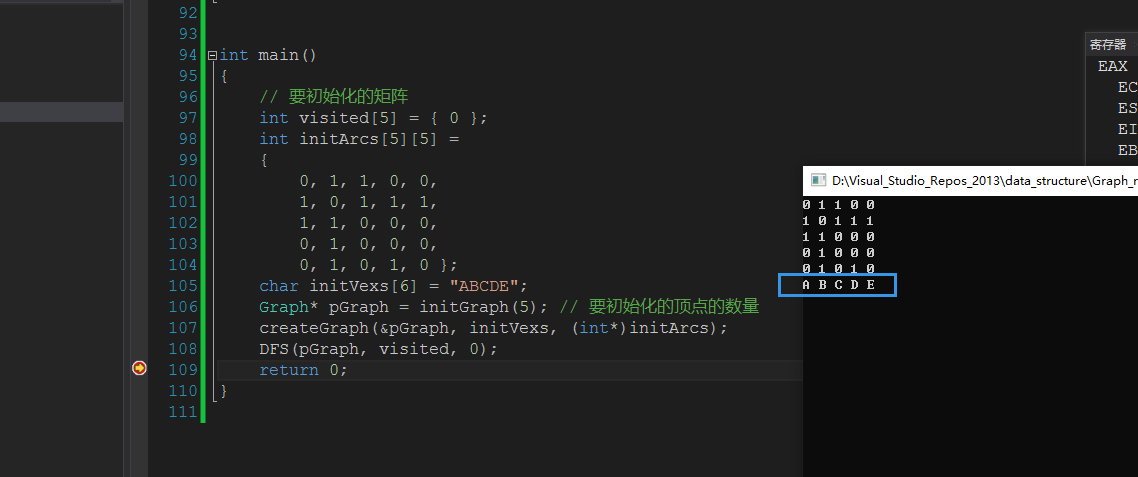
Status BFS(Graph* pGraph, int* iVisitedArray, int visitedIndex)
{
	SQueue sQueue;
	if (pGraph == NULL)
		return ERROR;
	initQueue(&sQueue, 10);
	iVisitedArray[visitedIndex] = 1;
	insertQueueElement(&sQueue, pGraph->vexs[visitedIndex]);
	while (!isQueueEmpty(&sQueue))
	{
		ElemType elem = deleteQueueElement(&sQueue);
		printf("%c ", elem);
		for (int i = 0;i<pGraph->vexNum;i++)
		{
			for (int j = 0;j<pGraph->vexNum;j++)
			{
				// printf("%d %d\n", pGraph->arcs[i][j], iVisitedArray[visitedIndex]);
				if (pGraph->arcs[i][j] == 1 && !iVisitedArray[j])
				{
					iVisitedArray[j] = 1;
					insertQueueElement(&sQueue, pGraph->vexs[j]);
				}
			}
		}
	}
 
	return OK;	
}
 
 
int main()
{
	// 要初始化的矩阵
	int visited[5] = { 0 };
	int initArcs[5][5] =
	{
		0, 1, 1, 0, 0,
		1, 0, 1, 1, 1,
		1, 1, 0, 0, 0,
		0, 1, 0, 0, 0,
		0, 1, 0, 1, 0 };
	char initVexs[6] = "ABCDE";
	Graph* pGraph = initGraph(5); // 要初始化的顶点的数量
	createGraph(&pGraph, initVexs, (int*)initArcs);
	//DFS(pGraph, visited, 0);
	BFS(pGraph, visited, 0);
	return 0;
}