栈实现中缀转后缀算术表达式以及运算结果
前言:数据结构中的笔记,通过栈来实现算术表达式
对于括号的处理,我这个还是需要完善下的,因为不能递进处理多个括号,因为我只写了处理一个括号的标识符,如果需要支持多个括号处理的话,那么就需要有对应的多个括号的标识符。
中缀表达式的加减乘除符号转换为后缀表达式
算数表达式是,自己实现的思路就是通过栈的结构来实现将中缀表达式转换到后缀表达式
实现中缀转后缀表达式并且实现运算需要总共执行如下两步操作
-
第一步 -> 实现中缀转化后缀
-
第二步 -> 实现解析后缀表达式来进行计算结果
比如存在一个中缀表达式为:1+2-3*4/2+5,那么对应的后缀表达式就是12+34*2/-5+
转换的思路如下,我自己画了一张图来进行表达
-
首先就是遇到操作数的话,那么就直接存储到用于存储后缀表达式中的字符串中
-
如果遇到的是操作符的话,就比如是
+-*/这种符号,那么我们就先压入到栈中 -
等待下一次的操作符,这时候就需要判断了,我们需要判断这次的操作符是否需要压入到栈中
那么判断的依据是什么呢?
这里需要给操作符设置优先级,就比如'+-'优先级为1,'*/'优先级为2
如果第一次压入到栈中的是'+-',然后第二次遇到的操作符是'/',那么这种情况下继续将'/'的操作符压入到栈中即可
如果第一次压入到栈中的是'/',然后第二次遇到的操作符是'+-',那么这次的话就需要将'/'弹出到后缀表达式中的字符串中,然后将其'+-'再压入到栈中
总结下就是如果遇到的操作符每次都需要遍历一次栈中的字符,如果优先级是大于或者等于当前运算符的,就都要弹出,将其复制到后缀表达式的字符串中
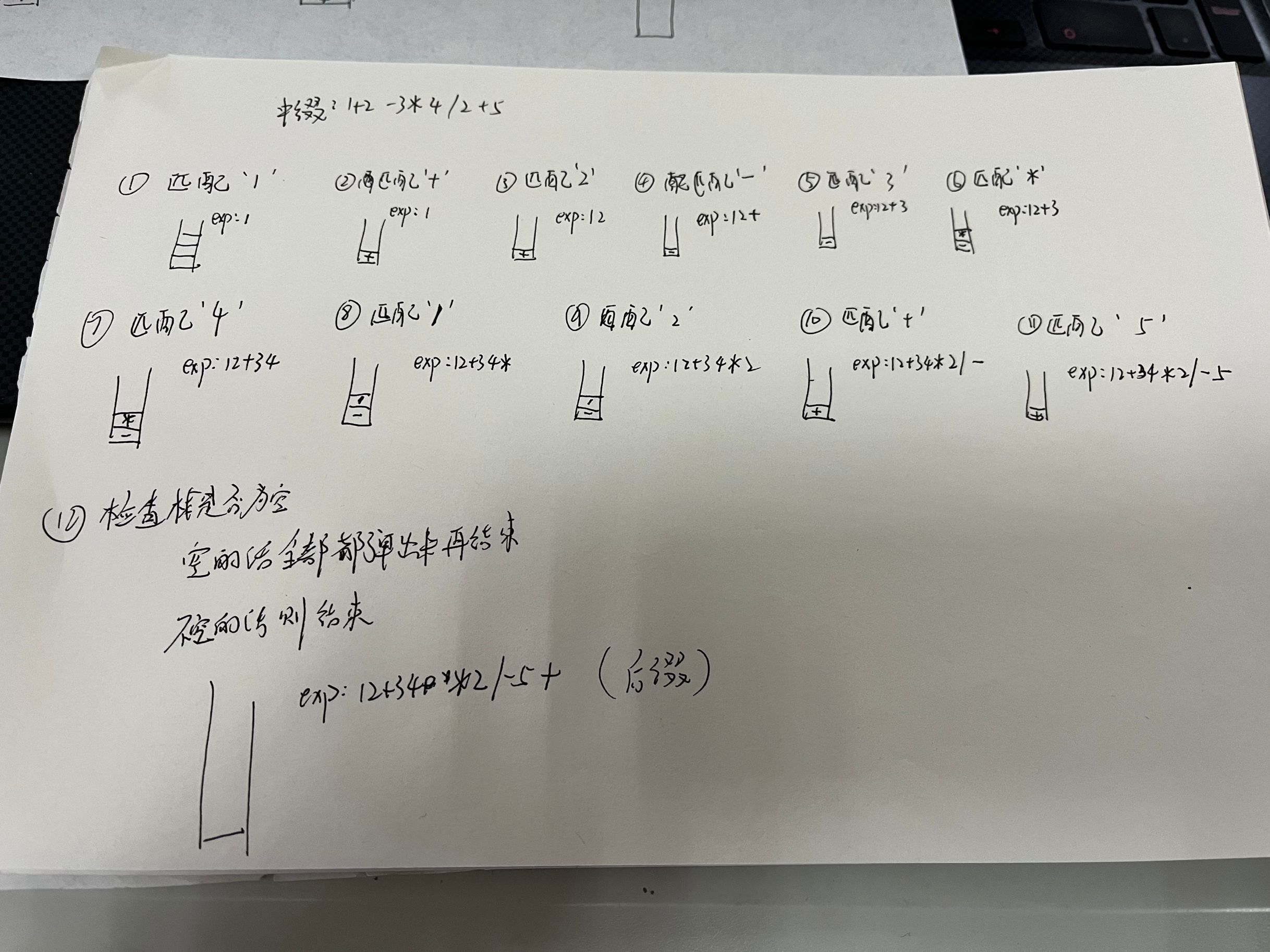
代码实现如下
#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#define OK 1
#define ERROR 0
#define MAXSIZE 99
typedef int Status;
typedef int ElemType;
typedef struct _SqStack
{
int iInitSize;
int iCurrentLength;
ElemType* pStack;
ElemType* pTop;
ElemType* pBottom;
}SqStack, *PSqStack;
typedef struct _OperatorPriority
{
int add_sub;
int mul_div;
int bracket;
}OperatorPriority, POperatorPriority;
// 用于后缀表达式中进行填充的时候所使用的
typedef struct _PofixExpression
{
ElemType leftOpera;
ElemType rightOpera;
ElemType opcode;
}PofixExpression, *PPofixExpression;
Status checkMemoryValidAddress(void* pAddr)
{
return pAddr != NULL ? OK : ERROR;
}
Status initStack(SqStack* pSqStack, int iSize)
{
pSqStack->pStack = malloc(sizeof(int)*iSize);
if (checkMemoryValidAddress((void*)pSqStack->pStack) == ERROR) return ERROR;
pSqStack->iInitSize = iSize;
pSqStack->pBottom = pSqStack->pTop = pSqStack->pStack;
pSqStack->iCurrentLength = 0;
return OK;
}
Status pushElem(SqStack* pSqStack, ElemType elem)
{
// juege between top and length
if (pSqStack->iCurrentLength == pSqStack->iInitSize)
return ERROR;
*pSqStack->pTop++ = elem;
pSqStack->iCurrentLength++;
return OK;
}
ElemType popElem(SqStack* pSqStack)
{
ElemType elem;
if (pSqStack->pTop == pSqStack->pBottom)
return ERROR;
elem = *--pSqStack->pTop;
pSqStack->iCurrentLength--;
return elem;
}
// 获取栈顶元素
ElemType getHeadElem(SqStack* pSqStack)
{
ElemType* pTempTop = pSqStack->pTop;
return *--pTempTop;
}
Status checkStackEmpty(SqStack* pSqStack)
{
if (pSqStack->pTop == pSqStack->pBottom)
return OK;
else
return ERROR;
}
// get symbol priority
int getSymbolPriority(char ch)
{
// + -
if (ch == '+' || ch == '-')
{
return 1;
}
// * /
else if (ch == '*' || ch == '/')
{
return 2;
}
// ( )
else if (ch == '(' || ch == ')')
{
return 3;
}
return 0;
}
char* initPofixExpression()
{
char *pPofixExpression = (char*)malloc(256 * sizeof(char));
memset(pPofixExpression, 0, 256 * sizeof(char));
if (pPofixExpression == NULL) return ERROR;
return pPofixExpression;
}
// 实现中缀表达式转换为后缀表达式
// get a pofix expression from middle expression
Status Middle2PofixNoBracket(SqStack* pSqStack, char* pMiddleExpression)
{
char* pInitPofixExpression = initPofixExpression(); // 用来存储后缀表达式的字符串
char* pMiddleChar = pMiddleExpression; // 当前的中序表达式的字符串
char* pPostChar = pInitPofixExpression; // 用来存储后缀表达式的字符串
while (*pMiddleChar != '\0')
{
if (*pMiddleChar >= '0' && *pMiddleChar <= '9')
*pPostChar++ = *pMiddleChar; // 遇到操作数就直接加入到后缀表达式中的字符串中去
else if (*pMiddleChar == '+' || *pMiddleChar == '-' || *pMiddleChar == '*' || *pMiddleChar == '/')
{
if (checkStackEmpty(pSqStack))
pushElem(pSqStack, *pMiddleChar);// 还需要看栈中是否为空,如果为空的话 那么运算符就先压入到栈中
else{
// 如果不是为空的话,那么就遍历栈,弹出其中优先高于或者等于当前运算符的,接着加入到后缀表达式中
while (1)
{
// 比较优先级
if (getSymbolPriority(getHeadElem(pSqStack)) >= getSymbolPriority(*pMiddleChar))
{
// 优先于的情况如果是大于的情况,那么需要弹出当前栈顶的元素
*pPostChar++ = popElem(pSqStack);
}
else
{
// 比较优先级的情况如果是小于的情况,那么还是将当前的操作符压入到栈中
pushElem(pSqStack, *pMiddleChar);
break;
}
}
}
}
pMiddleChar++;
}
// 走到这里的话表示的是字符串中的字符已经匹配完成了,但是此时栈中还存在剩余的运算符,那么就需要将这些运算符都弹出来
while (!checkStackEmpty(pSqStack))
*pPostChar++ = popElem(pSqStack);
printf("pInitPofixExpression: %s\n", pInitPofixExpression);
return OK;
}
// 实现中缀转后缀表达式并且实现运算需要总共执行两步操作
// 第一步 -> 实现中缀转化后缀
// 第二步 -> 实现解析后缀表达式来进行计算结果
int main()
{
SqStack sqStack;
ElemType calcResult = 0;
char middleExpression[MAXSIZE] = { 0 };
int iSize;
printf("init stack size -> ");
scanf("%d", &iSize);
// 初始化栈结构
initStack(&sqStack, iSize);
// 初始化中缀表达式
printf("init middleExpression -> ");
scanf("%s", middleExpression);
// 中缀转换后缀表达式
Middle2Pofix(&sqStack, middleExpression);
// 初始化栈结构
memset(&sqStack, 0, sizeof(SqStack));
initStack(&sqStack, iSize);
// 后缀表达式计算结果
// getOperaResult(&sqStack, pPofixExpression, &calcResult);
// 打印计算结果
printf("calc result -> %d\n", calcResult);
return 0;
}
测试数据: 1+2-3*4/2+5,发现是可以成功转化为后缀表达式 12+34*2/-5+
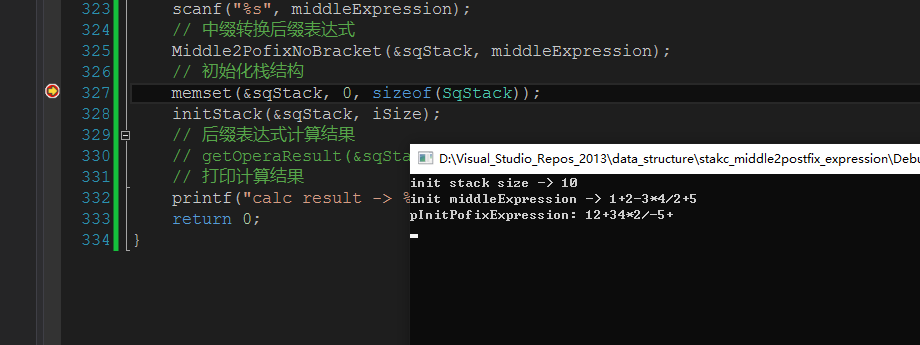
中缀表达式的加减乘除符号加上括号转换为后缀表达式
我同样画了一张图,如下所示
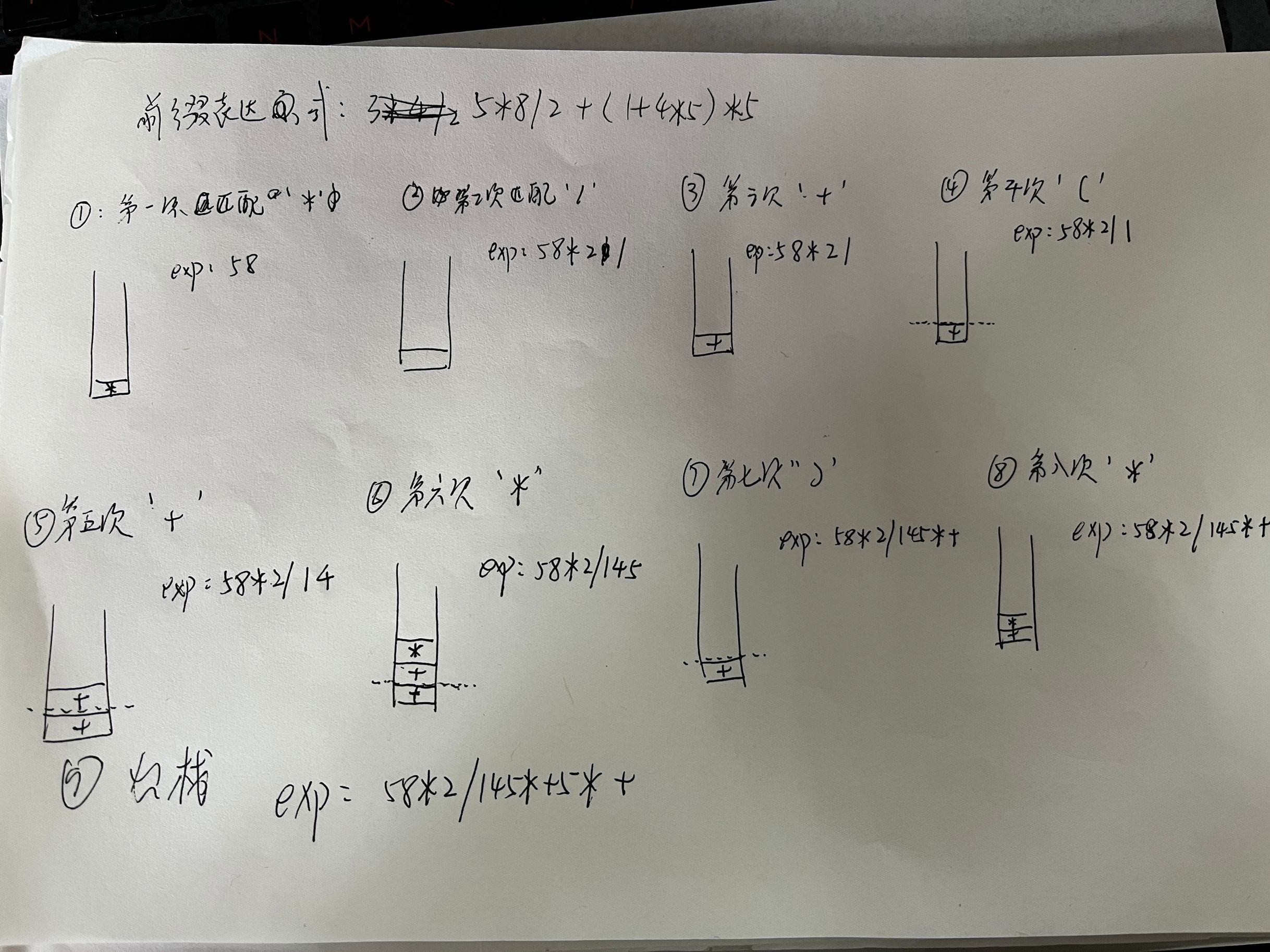
实现代码如下
#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#define OK 1
#define ERROR 0
#define MAXSIZE 99
typedef int Status;
typedef int ElemType;
typedef struct _SqStack
{
int iInitSize;
int iCurrentLength;
ElemType* pStack;
ElemType* pTop;
ElemType* pBottom;
}SqStack, *PSqStack;
typedef struct _OperatorPriority
{
int add_sub;
int mul_div;
int bracket;
}OperatorPriority, POperatorPriority;
// 用于后缀表达式中进行填充的时候所使用的
typedef struct _PofixExpression
{
ElemType leftOpera;
ElemType rightOpera;
ElemType opcode;
}PofixExpression, *PPofixExpression;
Status checkMemoryValidAddress(void* pAddr)
{
return pAddr != NULL ? OK : ERROR;
}
Status initStack(SqStack* pSqStack, int iSize)
{
pSqStack->pStack = malloc(sizeof(int)*iSize);
if (checkMemoryValidAddress((void*)pSqStack->pStack) == ERROR) return ERROR;
pSqStack->iInitSize = iSize;
pSqStack->pBottom = pSqStack->pTop = pSqStack->pStack;
pSqStack->iCurrentLength = 0;
return OK;
}
Status pushElem(SqStack* pSqStack, ElemType elem)
{
// juege between top and length
if (pSqStack->iCurrentLength == pSqStack->iInitSize)
return ERROR;
*pSqStack->pTop++ = elem;
pSqStack->iCurrentLength++;
return OK;
}
ElemType popElem(SqStack* pSqStack)
{
ElemType elem;
if (pSqStack->pTop == pSqStack->pBottom)
return ERROR;
elem = *--pSqStack->pTop;
pSqStack->iCurrentLength--;
return elem;
}
// 获取栈顶元素
ElemType getHeadElem(SqStack* pSqStack)
{
ElemType* pTempTop = pSqStack->pTop;
return *--pTempTop;
}
Status checkStackEmpty(SqStack* pSqStack)
{
if (pSqStack->pTop == pSqStack->pBottom)
return OK;
else
return ERROR;
}
// get symbol priority
int getSymbolPriority(char ch)
{
// + -
if (ch == '+' || ch == '-')
{
return 1;
}
// * /
else if (ch == '*' || ch == '/')
{
return 2;
}
// ( )
else if (ch == '(' || ch == ')')
{
return 3;
}
return 0;
}
char* initPofixExpression()
{
char *pPofixExpression = (char*)malloc(256 * sizeof(char));
memset(pPofixExpression, 0, 256 * sizeof(char));
if (pPofixExpression == NULL) return ERROR;
return pPofixExpression;
}
// 实现中缀表达式转换为后缀表达式
// 有括号的情况
// 测试数据 -> 5*8/2+(1+4*5)*5 -> 58*2/145*+5*+
Status Middle2Pofix(SqStack* pSqStack, char* pMiddleExpression)
{
char* pInitPofixExpression = initPofixExpression(); // 用来存储后缀表达式的字符串
char* pMiddleChar = pMiddleExpression; // 当前的中序表达式的字符串
char* pPostChar = pInitPofixExpression; // 用来存储后缀表达式的字符串的内存空间
int iBracketFlag = 0; // bracket标识符
while (*pMiddleChar != '\0')
{
if (*pMiddleChar >= '0' && *pMiddleChar <= '9')
*pPostChar++ = *pMiddleChar;
else if (*pMiddleChar == '+' || *pMiddleChar == '-' || *pMiddleChar == '*' || *pMiddleChar == '/')
{
// 正常匹配的情况 -> 遇到运算符的情况下需要遍历一次栈,弹出其中优先级高于或者等于当前的运算符的,并加入到后缀表达式中去
// 还需要看栈中是否为空,如果为空的话 那么运算符就先压入到栈中
if (checkStackEmpty(pSqStack))
pushElem(pSqStack, *pMiddleChar);
else{
// 如果不是为空的话,那么就遍历栈,弹出其中优先高于或者等于当前运算符的,接着加入到后缀表达式中
if (iBracketFlag == 0)
{
while (1)
{
// 比较优先级
if (getSymbolPriority(getHeadElem(pSqStack)) >= getSymbolPriority(*pMiddleChar))
*pPostChar++ = popElem(pSqStack); // 那么需要弹出当前栈顶的元素
else
{
pushElem(pSqStack, *pMiddleChar); // 比较优先级的情况如果是小于的情况,那么还是将当前的操作符压入到栈中
break;
}
}
}
else
{
// 在有左括号的情况下,这个时候就不能正常处理了,原因解释下,首先需要知道的是括号的优先级最高
// 此时如果左括号压进去了,接着你匹配到一个+号,那么正常来走的话就意味着需要直接把括号直接出栈,
// 但是如果这样子的话那肯定就不行了 正常的话括号肯定是不能直接出的
// 所以说如果有左括号已经被压进去了,接着一个+号,那么还需要等下一个来运算符来了之后才能判断这个+号能否执行
while (iBracketFlag == 1)
{
// 比较优先级
if (getSymbolPriority(getHeadElem(pSqStack)) >= getSymbolPriority(*pMiddleChar) && getHeadElem(pSqStack) != '(')
*pPostChar++ = popElem(pSqStack); // 那么需要弹出当前栈顶的元素
else
{
// 比较优先级的情况如果是小于的情况,那么还是将当前的操作符压入到栈中
pushElem(pSqStack, *pMiddleChar);
break;
}
}
}
}
}
else if (*pMiddleChar == '(')
{
iBracketFlag = 1; // 此时已经匹配到了左括号
pushElem(pSqStack, *pMiddleChar);
}
else if (*pMiddleChar == ')')
{
while (1)
{
if (getHeadElem(pSqStack) != '(')
*pPostChar++ = popElem(pSqStack);
else
{
popElem(pSqStack);
iBracketFlag = 0;
break;
}
}
}
pMiddleChar++;
}
// 走到这里的话表示的是字符串中的字符已经匹配完成了,但是此时栈中还存在剩余的运算符,那么就需要将这些运算符都弹出来
while (!checkStackEmpty(pSqStack))
*pPostChar++ = popElem(pSqStack);
printf("pInitPofixExpression: %s\n", pInitPofixExpression);
return OK;
}
// 实现中缀转后缀表达式并且实现运算需要总共执行两步操作
// 第一步 -> 实现中缀转化后缀
// 第二步 -> 实现解析后缀表达式来进行计算结果
int main()
{
// test -> 1+2-3*4/2+5
SqStack sqStack;
ElemType calcResult = 0;
char middleExpression[MAXSIZE] = { 0 };
int iSize;
printf("init stack size -> ");
scanf("%d", &iSize);
// 初始化栈结构
initStack(&sqStack, iSize);
// 初始化中缀表达式
printf("init middleExpression -> ");
scanf("%s", middleExpression);
// 中缀转换后缀表达式
// Middle2PofixNoBracket(&sqStack, middleExpression);
Middle2Pofix(&sqStack, middleExpression);
// 初始化栈结构
memset(&sqStack, 0, sizeof(SqStack));
initStack(&sqStack, iSize);
// 后缀表达式计算结果
// getOperaResult(&sqStack, pPofixExpression, &calcResult);
// 打印计算结果
printf("calc result -> %d\n", calcResult);
return 0;
}
测试数据:5*8/2+(1+4*5)*5 -> 58*2/145*+5*+
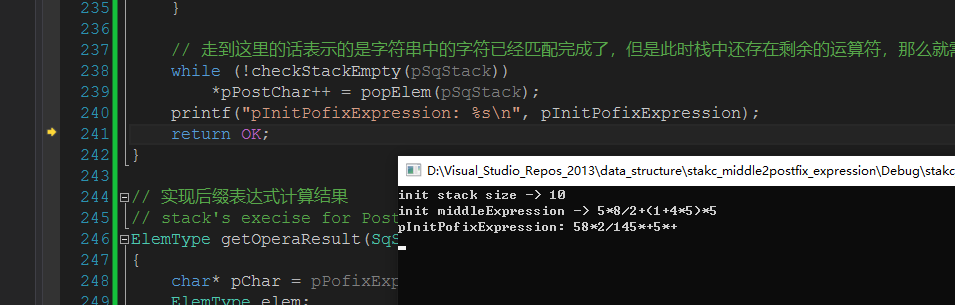
测试数据:5*8/2+(1-2*3-4)*5 -> 58*2/123*-4-5*+
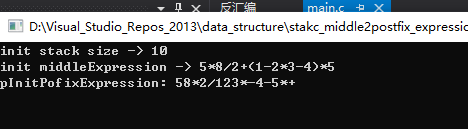
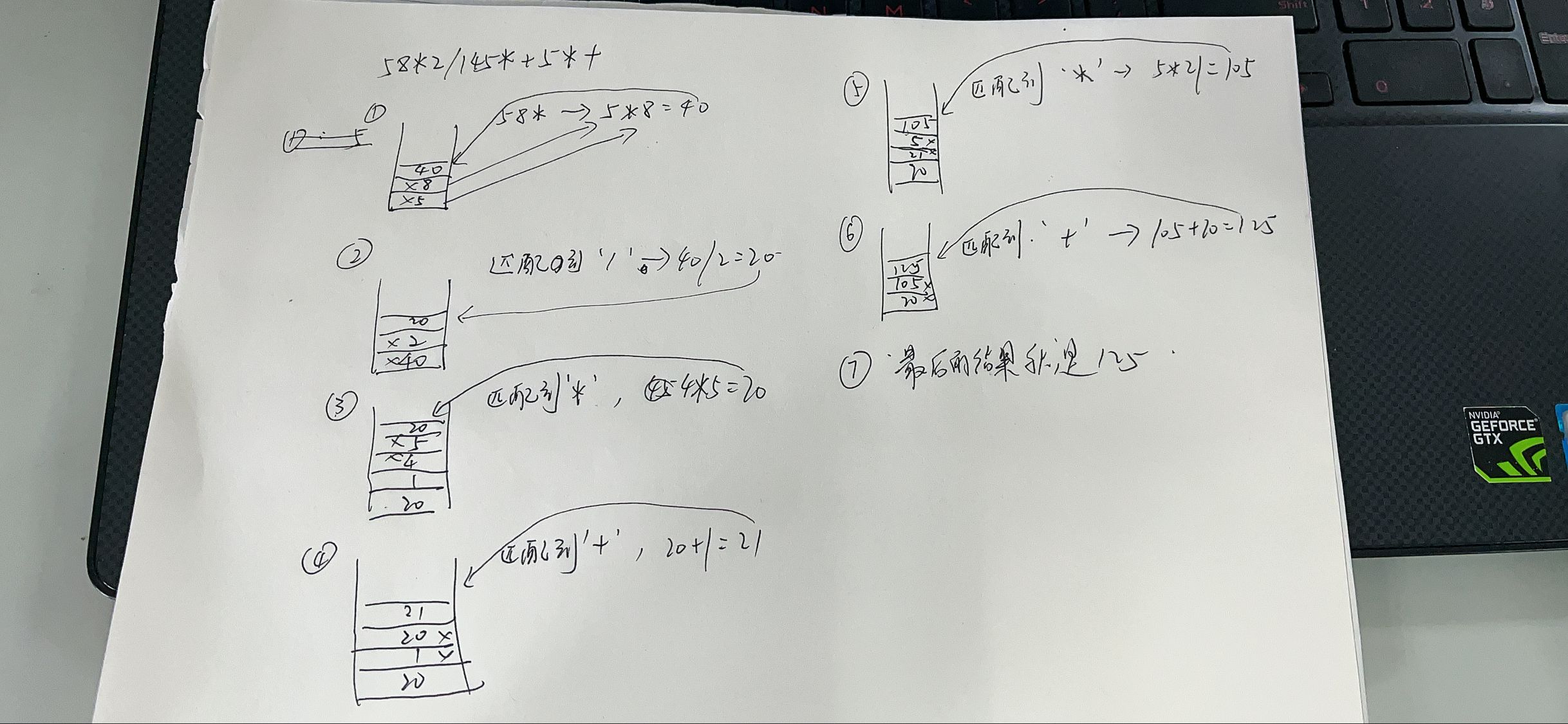
如何进行运算结果
我这里也同样画了一张画来进行演示,这里比如就是 中缀表达式 5*8/2+(1+4*5)*5 -> 后缀表达式 58*2/145*+5*+
代码实现如下:
// 实现后缀表达式计算结果
// stack's execise for Postfix Expression
ElemType getOperaResult(SqStack* pSqStack, char* pPofixExpression, ElemType* calcResult)
{
char* pChar = pPofixExpression;
ElemType elem;
PofixExpression* pExpression = (PofixExpression*)malloc(sizeof(PofixExpression));
while (*pChar != '\0')
{
// 1+2-2*2/2+5 -> 12+22*2/-5+
if (*pChar >= '0' && *pChar <= '9')
{
pushElem(pSqStack, *pChar);
}
else if (*pChar == '+' || *pChar == '-' || *pChar == '*' || *pChar == '/')
{
// 数值填充
elem = popElem(pSqStack);
pExpression->rightOpera = elem;
elem = popElem(pSqStack);
pExpression->leftOpera = elem;
// 符号填充
pExpression->opcode = *pChar;
// + - * /的运算
switch (pExpression->opcode)
{
case '+':
elem = (pExpression->leftOpera - '0') + (pExpression->rightOpera - '0');
printf("%d %c %d = %d\n", (pExpression->leftOpera - '0'), pExpression->opcode, (pExpression->rightOpera - '0'), elem);
break;
case '-':
elem = (pExpression->leftOpera - '0') - (pExpression->rightOpera - '0');
printf("%d %c %d = %d\n", (pExpression->leftOpera - '0'), pExpression->opcode, (pExpression->rightOpera - '0'), elem);
break;
case '*':
elem = (pExpression->leftOpera - '0') * (pExpression->rightOpera - '0');
printf("%d %c %d = %d\n", (pExpression->leftOpera - '0'), pExpression->opcode, (pExpression->rightOpera - '0'), elem);
break;
case '/':
elem = (pExpression->leftOpera - '0') / (pExpression->rightOpera - '0');
printf("%d %c %d = %d\n", (pExpression->leftOpera - '0'), pExpression->opcode, (pExpression->rightOpera - '0'), elem);
break;
default:
break;
}
// 运算结果重新填充回栈中为下一次做好准备
pushElem(pSqStack, elem + '0');
}
// while循环下一次继续遍历
pChar++;
}
*calcResult = popElem(pSqStack);
return OK;
}
// 实现中缀转后缀表达式并且实现运算需要总共执行两步操作
// 第一步 -> 实现中缀转化后缀
// 第二步 -> 实现解析后缀表达式来进行计算结果
int main()
{
// test -> 1+2-3*4/2+5
SqStack sqStack;
ElemType calcResult = 0;
char middleExpression[MAXSIZE] = { 0 };
char* pPofixExpression = NULL;
int iSize;
printf("init stack size -> ");
scanf("%d", &iSize);
// 初始化栈结构
initStack(&sqStack, iSize);
// 初始化中缀表达式
printf("init middleExpression -> ");
scanf("%s", middleExpression);
// 中缀转换后缀表达式
// Middle2PofixNoBracket(&sqStack, middleExpression);
pPofixExpression = Middle2Pofix(&sqStack, middleExpression);
memset(&sqStack, 0, sizeof(SqStack));
initStack(&sqStack, iSize);
// 后缀表达式计算结果
getOperaResult(&sqStack, pPofixExpression, &calcResult);
// 打印计算结果
printf("calc result -> %d\n", calcResult - '0');
return 0;
}
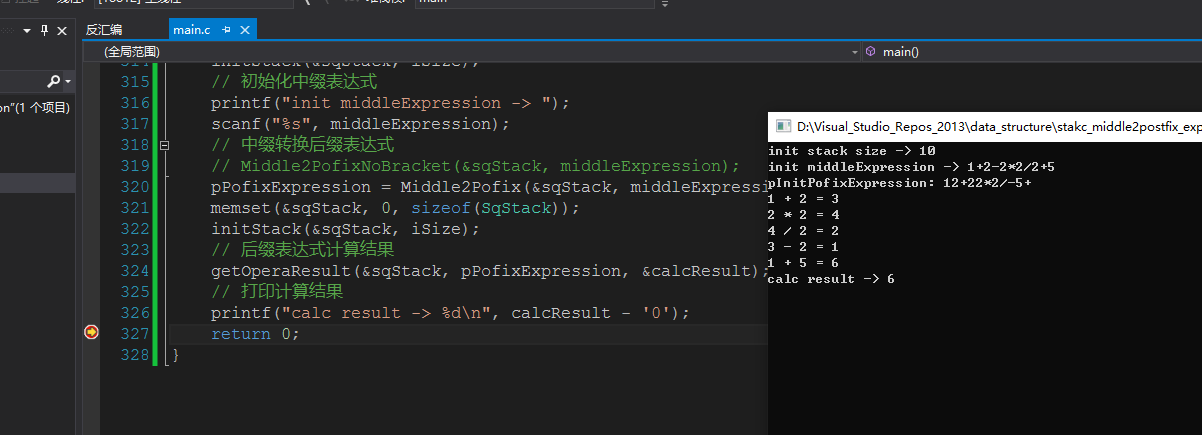
测试数据:1+2-3*4/2+5 -> 12+22*2/-5+



 浙公网安备 33010602011771号
浙公网安备 33010602011771号