Codeforces Round 871 (Div. 4)D~G

Codeforces Round 871 (Div. 4)D~G

D. Gold Rush（递归）

题意

给一个数n，可以分成两份，其中一份是另一份的两倍

思路

当前有数num，那它就是由3 * num或者1.5 * num得来的

• 3 * num可以分成num和2 * num，此时num是比较小的那份
• 1.5 * num可以分成0.5 * num和num，此时num是较大的那份

于是就可以从num开始递归往大的数字找，看看有没有数字能分成num

代码

#include<bits/stdc++.h>
#define endl '\n'
#define int long long
using namespace std;
vector<string>ans;
int n, m;
bool search(int num) {
	if (num > 1e7 || num > n)return false;
	if (num == n)return true;
	if ((num & 1) == 1) {	// 奇数
		return search(3 * num);
	}
	else {
		return search(3 * num) || search(num + (num >> 1));
	}
}

void solve() {
	cin >> n >> m;
	if (search(m))ans.push_back("YES");
	else ans.push_back("NO");
}

signed main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr);

	int _; _ = 1;
	cin >> _;
	while (_--)	solve();
	for (auto x : ans)cout << x << endl;
	return 0;
}
/*
	要得到m，必须有3m或者1.5m
*/

E. The Lakes（DFS）

题意

给的数组里面，大于0的数字可以靠上下左右连在一起算一个连通块，每格的贡献就是格子的值。求所有连通块里面权值最大的

思路

直接DFS找每一个连通块

代码

#include<bits/stdc++.h>
#define endl '\n'
#define int long long
using namespace std;
vector<long long>ans;
const int N = 1e3 + 5;

int dx[] = { -1,1,0,0 };
int dy[] = { 0,0,-1,1 };
int mp[N][N];
int n, m;
int maxS, cnt;
void dfs(int x, int y) {
	for (int i = 0; i < 4; i++) {
		int nx = x + dx[i];
		int ny = y + dy[i];
		if (1 > nx || 1 > ny || nx > n || ny > m || mp[nx][ny] == 0)continue;
		cnt += mp[nx][ny];
		mp[nx][ny] = 0;
		dfs(nx, ny);
	}
}

void solve() {
	//memset(mp, 0, sizeof(mp));
	maxS =0;
	cnt = 0;
	cin >> n >> m;
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= m; j++) {
			cin >> mp[i][j];
		}
	}
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= m; j++) {
			if (mp[i][j]) {
				cnt += mp[i][j];
				mp[i][j] = 0;
				dfs(i, j);
				maxS = max(maxS, cnt);
				cnt = 0;
			}
		}
	}
	ans.push_back(maxS);
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= m; j++) {
			mp[i][j] = 0;
		}
	}
}

signed main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr);

	int _; _ = 1;
	cin >> _;
	while (_--)	solve();
	for (auto x : ans)cout << x << endl;
	return 0;
}

F. Forever Winter（图）

题意

会给一个很特别的图，然后要求有多少个新顶点连中心顶点，又有多少个点连那些连中心顶点的点

思路

靠瞪眼，发现可以算出来每个点的入度。算出来的入度种类只有两种可能，要么有两种不同的入度，要么有三种不同的入度

叶子顶点的入度一定是1（无向图），此时看其他的入度

• 两种不同的入度

  当x=y+1的时候，会导致只有两种不同的入度

  比如x=3，y=2

  中心顶点的入度为3，连接中心顶点的点入度也为3

  除了为1的那个入度，另一个入度num，num就是x，num-1就是y
  

• 三种不同的入度

  也就是x!=y+1的时候，有三种不同的入度

  同样不看为1的那个入度，只出现了一次的入度num1，那就是中心顶点的入度，而另一个入度num2就是连接中心顶点的入度

  num1 = x

  num2 = y+1

所以分类讨论一下

代码

#include<bits/stdc++.h>
#define endl '\n'
#define int long long
using namespace std;
vector<long long>ans;
const int N = 205;
int indegree[N];

void solve() {
	memset(indegree, 0, sizeof(indegree));
	int n, m; cin >> n >> m;
	for (int i = 0, u, v; i < m; i++) {
		cin >> u >> v;
		indegree[u]++;
		indegree[v]++;
	}
	set<int>s;
	map<int, int>mp;
	for (int i = 1; i <= n; i++) {
		s.insert(indegree[i]);
		mp[indegree[i]]++;
	}
	int x, y;
	vector<int>v;
	for (auto& num : s) {
		v.push_back(num);
	}
	sort(v.begin(), v.end());
	if (v.size() == 2) {
		cout << v[1] << " " << v[1] - 1 << endl;
		return;
	}
	if (mp[v[2]] == 1) {
		x = v[2];
		y = v[1];
	}
	else {
		x = v[1];
		y = v[2];
	}
	if (y > 1)y--;
	cout << x << " " << y << endl;
}

signed main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr);

	int _; _ = 1;
	cin >> _;
	while (_--)	solve();
	for (auto x : ans)cout << x << endl;
	return 0;
}

G. Hits Different（递归）

题意

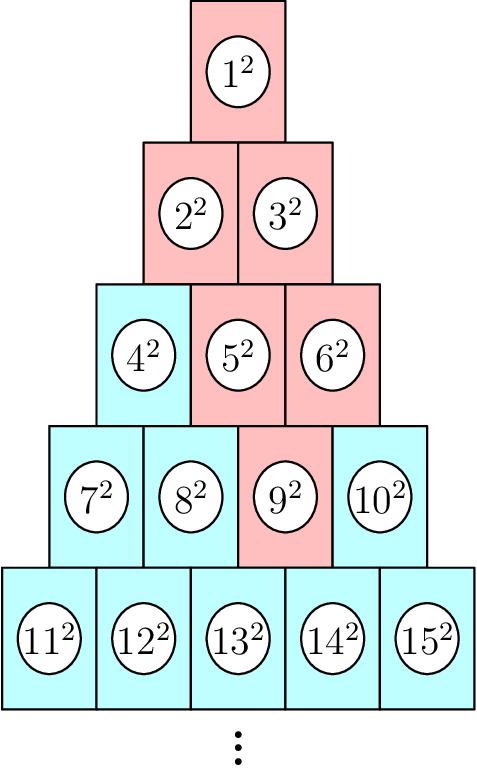
一个金字塔，上面放了num²，如果推到一个，会按照图示那样，把上面的也推到，问推到某个数的时候，总共倒了多少

思路

很容易就可以写出来暴力递归的写法，从下往上计算，搞个vis数组，标记这个罐头计算过没有，然后继续往上累加

#include<bits/stdc++.h>
#define endl '\n'
#define int long long
using namespace std;
vector<long long>ans;

long long mp[3000][3000];
int vis[3000][3000];
long long fun(int x, int y) {
	if (vis[x][y])return 0;
	vis[x][y] = 1;
	long long sum = mp[x][y];
	if (x - 1 >= 1 && y - 1 >= 1) {
		sum += fun(x - 1, y - 1);
	}
	if (x - 1 >= 1 && y <= x - 1) {
		sum += fun(x - 1, y);
	}
	return sum;
}

void solve() {
	long long n; cin >> n;
	// 对于每个被击倒的易拉罐，它总会影响它上面以及右上的
	long long cur = 1;
	int i = 1, j;
	bool flag = false;
	for (; i <= 2023; i++) {
		for (j = 1; j <= i; j++) {
			if (cur == n) {
				flag = true;
				break;
			}
			cur++;
		}
		if (flag)break;
	}
	// 从i，j开始往上
	ans.push_back(fun(i, j));
	for (int a = 1; a <= i; a++) {
		for (int b = 1; b <= a; b++) {
			vis[a][b] = 0;
		}
	}
}

signed main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr);

	int _; _ = 1;
	cin >> _;
	long long num = 1;
	for (int i = 1; i <= 2023; i++) {
		for (int j = 1; j <= i; j++) {
			mp[i][j] = num * num;
			num++;
		}
	}
	while (_--)	solve();
	for (auto x : ans)cout << x << endl;
	return 0;
}

这样就顺利的T了，因为最多2000多层，只靠原本的金字塔来计算肯定会T

所以还是要直接求出：推倒n的时候，直接得到了多少

假设推倒某个数字num，可以得到mp

很容易想到 mp[i][j] = num*num + mp[i-1][j-1] + mp[i-1][j]

但是这样就会重复：比如推9，按照式子，得到的就是5和6的值，其实重复计算了3一次，所以要减掉

变成 mp[i][j] = num*num + mp[i-1][j-1] + mp[i-1][j] - mp[i-2][j-1]

代码

#include<bits/stdc++.h>
#define endl '\n'
#define int long long
using namespace std;
vector<long long>ans;
const int N = 2050;
long long mp[N][N];
long long res[N*N];
void fun() {
	long long num = 1;
	for (int i = 1; i <= 2023; i++) {
		for (int j = 1; j <= i; j++) {
			mp[i][j] = (i == 1 ? 1 : num * num + mp[i - 1][j - 1] + mp[i - 1][j] - mp[i - 2][j - 1]);
			res[num] = mp[i][j];
			num++;
		}
	}
}

void solve() {
	int n; cin >> n;
	ans.push_back(res[n]);
}

signed main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr);

	int _; _ = 1;
	cin >> _;
	fun();
	while (_--)	solve();
	for (auto x : ans)cout << x << endl;
	return 0;
}