Codeforces Round 993 (Div. 4)DEG
Codeforces Round 993 (Div. 4)DEG
D. Harder Problem(构造)
题意
给一个长度为n的数组a,然后构造一个长度为n的数组b,ai 是数组 b 前 i 个数的众数,1 <= bi <= n
思路
- 题目有说如果数字出现次数相同,都是最大的。那他们都是众数,所以可以让1~n每一个数字都出现一次,那最后每一个数字都是众数,关键是调整一下1~n这n个数字的出现顺序而已
- 因为我们只让1~n每个数字出现一次,所以对于ai是前i个数的众数,如果ai已经出现了,那再随便填一个数字就可以,只要不让已经出现过的数字重复出现就可以(这样就使得所有数字出现次数都是1,所有数字都是众数)
代码
#include <iostream>
#include <vector>
#include <algorithm>
#include <set>
#define endl '\n'
using namespace std;
void solve() {
int n, num; cin >> n;
int cnt = 1; // cnt表示还没填过的最小的数字
vector<int>ans; // b数组
vector<int>vis(n + 1); // 标记数字是否出现过,用来更新cnt
set<int>s; // 记录数字在前面有没有填过
for (int i = 0; i < n; i++) {
cin >> num;
// 前面已经填过num了,现在填一个还没填过的最小的数字
if (s.count(num)) {
ans.push_back(cnt);
s.insert(cnt);
vis[cnt] = 1;
}
// 前面没填过num,现在补上
else {
ans.push_back(num);
s.insert(num);
vis[num] = 1;
}
// 更新还没填过的最小的数字
while (cnt <= n && vis[cnt]) {
cnt++;
}
}
for (auto x : ans) {
cout << x << " ";
}
cout << endl;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int _; cin >> _;
while (_--)
solve();
return 0;
}
E. Insane Problem(数学)
题意
给了y和x的范围,还有k的值,求满足 y / x = kn 的 (x,y)对数。
思路
-
kn最大不超过r2/l1的最大值1e9,然后就枚举n
-
这题把问题转换了一下,可以转换成求x的所有取值
y / x = kn ---> y = kn * x
l2 <= y <= r2 ---> l2 <= kn * x <= r2 ---> l2 / kn <= x <= r2 / kn
l1 <= x <= r1
然后取x的取值区间交集长度累加就是答案
左端点l = max(l2 / kn,l1),但是这里l2 / kn要向上取整
右端点r = min(r2 / kn,r1)
区间长度max(r-l+1,0)
代码
#include <iostream>
#include <cmath>
#include <vector>
#define endl '\n'
using namespace std;
vector<int>ans;
void solve() {
long long k, l1, r1, l2, r2; cin >> k >> l1 >> r1 >> l2 >> r2;
long long res = 0;
long long kn = 1;
while (kn <= 1e9) {
long long l = max(l1, (long long)ceil(l2 * 1.0 / kn*1.0));
long long r = min(r1, r2 / kn);
res += max(r - l + 1, 0ll);
kn *= k;
}
ans.push_back(res);
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int _; cin >> _;
while (_--)
solve();
for (auto x : ans) {
cout << x << endl;
}
return 0;
}
// y = kn * x
// y / kn = x
// l2/kn <= x <= r2/kn
G1. Medium Demon Problem (easy version)(拓扑排序,基环树)
题意
n个蜘蛛,每一轮第i个蜘蛛都会给第ri个蜘蛛一个玩具,如果手上的玩具超过一个,那也只会保留一个
思路
-
看一下样例画一下图,找到了规律
对于样例
10
4 3 9 1 6 7 9 10 10 3
发现就是:环外面的点,到环的距离最大值+2,那就直接拓扑排序,计算深度,因为每个点同一时刻收到多少东西,它这一次只要传递一次(多的直接扔了,这和hard version不一样)
![]()
代码
#include <iostream>
#include <cmath>
#include <vector>
#include <algorithm>
#include <cstring>
#include <queue>
#define endl '\n'
using namespace std;
const int N = 2e5 + 5;
int head[N],indegree[N],deep[N];
int cnt,n;
struct edge {
int to, nex;
}e[N];
vector<int>ans;
void addEdge(int x, int y) {
cnt++;
e[cnt].to = y;
e[cnt].nex = head[x];
head[x] = cnt;
indegree[y]++;
}
void init() {
memset(head, -1, sizeof(head));
memset(indegree, 0, sizeof(indegree));
memset(deep, 0, sizeof(deep));
cnt = 0;
cin >> n;
int v;
for (int i = 1; i <= n; i++) {
cin >> v;
addEdge(i, v);
}
}
void solve() {
init();
int v;
queue<int>q;
for (int i = 1; i <= n; i++) {
if (!indegree[i]) {
q.push(i);
}
}
int res = 0;
while (!q.empty()) {
int cur = q.front();
q.pop();
for (int j = head[cur]; j != -1; j = e[j].nex) {
v = e[j].to;
indegree[v]--;
// 代码关键就是这里,深度是最大值
deep[v] = max(deep[v], deep[cur] + 1);
res = max(res, deep[v]);
if (!indegree[v]) {
q.push(v);
}
}
}
ans.push_back(res + 2);
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int _; cin >> _;
while (_--)
solve();
for (auto x : ans) {
cout << x << endl;
}
return 0;
}
/*
找到环外点到环的距离,然后加2输出
*/
G2. Medium Demon Problem (hard version)
题意
这一次蜘蛛手上可以有多个玩具,但是每次只会传递一个玩具
思路
-
还是画个样例来看看
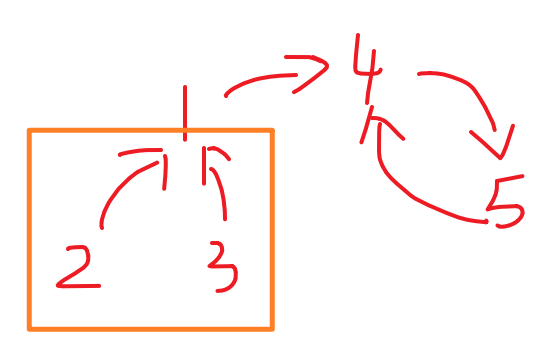
5
4 1 1 5 4
可以理解为,1节点要接受所有子树的东西,然后再一个一个传递进环。深度就变成了累加,而不是取更大的值
![]()
代码
#include <iostream>
#include <cmath>
#include <vector>
#include <algorithm>
#include <cstring>
#include <queue>
#define endl '\n'
using namespace std;
const int N = 2e5 + 5;
int head[N],indegree[N],deep[N];
int cnt,n;
struct edge {
int to, nex;
}e[N];
vector<int>ans;
void addEdge(int x, int y) {
cnt++;
e[cnt].to = y;
e[cnt].nex = head[x];
head[x] = cnt;
indegree[y]++;
}
void init() {
memset(head, -1, sizeof(head));
memset(indegree, 0, sizeof(indegree));
memset(deep, 0, sizeof(deep));
cnt = 0;
cin >> n;
int v;
for (int i = 1; i <= n; i++) {
cin >> v;
addEdge(i, v);
}
}
void solve() {
init();
int v;
queue<int>q;
for (int i = 1; i <= n; i++) {
if (!indegree[i]) {
q.push(i);
}
}
int res = 0;
while (!q.empty()) {
int cur = q.front();
q.pop();
for (int j = head[cur]; j != -1; j = e[j].nex) {
v = e[j].to;
indegree[v]--;
deep[cur]++; // 加上自己手上的
deep[v] += deep[cur]; // v接收所有子树的东西
// cur一定不在环内,v可能在环内,所以是取cur的最大值
//(因为是看环外的节点把所有东西传进环内的时间)
res = max(res, deep[cur]);
if (!indegree[v]) {
q.push(v);
}
}
}
ans.push_back(res + 2);
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int _; cin >> _;
while (_--)
solve();
for (auto x : ans) {
cout << x << endl;
}
return 0;
}



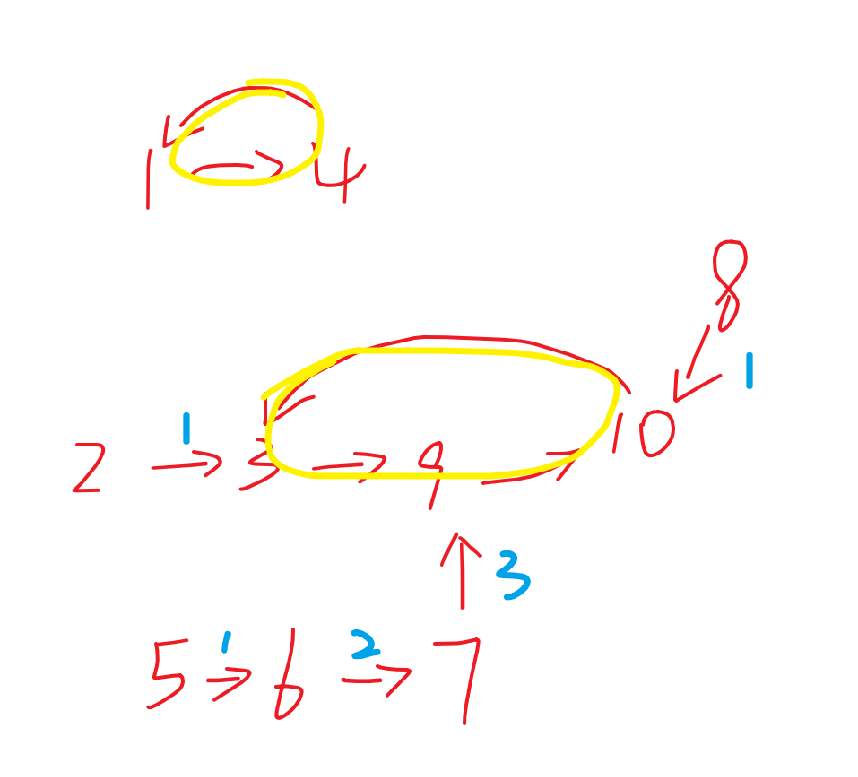

 浙公网安备 33010602011771号
浙公网安备 33010602011771号