同余定理+容斥原理

　　小学期的第二天，了解了一下同余定理。

　　在理解完这个同余定理以后感觉非常奇妙，可能就是数学的魅力？

　　即：给定一个正整数m，如果两个整数a和b满足（a-b）能够被m整除，即（a-b）/m得到一个整数，那么就称整数a与b对模m同余(a%c的值==b%c的值)，记作a≡b(mod m)。

　　基本应用：

　　1、(a + b) % p = (a % p + b % p) % p

　　2、(a - b) % p = (a % p - b % p) % p

　　3、(a * b) % p = (a % p * b % p) % p

　　4、 a^b % p = ((a % p)^b) % p

　　5、((a+b) % p + c) % p = (a + (b+c) % p) % p 

　　6、((a*b) % p * c)% p = (a * (b*c) % p) % p

　　7、(a + b) % p = (b+a) % p

　　8、(a * b) % p = (b * a) % p

　　9、((a +b)% p * c) % p = ((a * c) % p + (b * c) % p) % p

　　重要定理：

　　10、若a≡b (% p)，则对于任意的c，都有(a + c) ≡ (b + c) (%p)；

　　11、若a≡b (% p)，则对于任意的c，都有(a * c) ≡ (b * c) (%p)；

　　12、若a≡b (% p)，c≡d (% p)，则 (a + c) ≡ (b + d) (%p)，(a - c) ≡ (b - d) (%p)，(a * c) ≡ (b * d) (%p)，(a / c) ≡ (b / d) (%p)；

　　

　　然后就在我上手写博客的前一秒，被考了一道容斥原理的题，我又被吸引了过去。

　　http://www.fjutacm.com/Problem.jsp?pid=2332

　　一开始听到的题目是电灯泡数一共十的六次方个，我想的是建数组，然后下标假如能整除一个素数就加一，最后再遍历看数组里的数是奇还是偶就可以判断灯亮不亮，然而被告知这样做会时间超限，再一登上题发现是十的九次方，就更不能这么做，然后我就开始想其他方法。

　　因为知道是容斥原理相关的，虽然没了解过这个原理，但我猜想可能是三个圈然后有重合部分这样的模型，事实证明是这样的^^

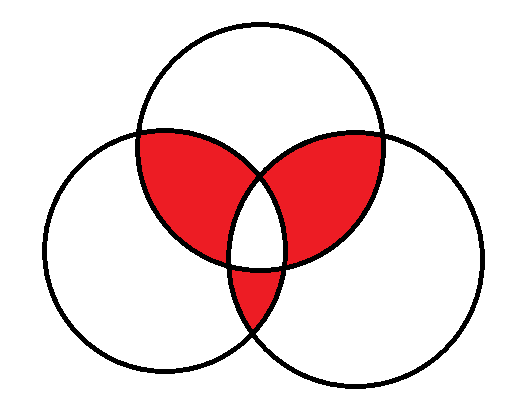
　　每一个大圈代表灯泡数除以一个素数，所以亮的部分就是所有白色，就可以得到公式：

　　sum=n/a+n/b+n/c-2*(n/(a*b)+n/(b*c)+n/(a*c))+4*(n/(a*b*c))直接输出就完事。

　　其中这道题我也犯了一个错误就是最后4*（n/a*b*c）部分时我没有加括号，导致wa了四次，果然细心是非常重要的，也算是教训。