Completions
完备化的过程是熟悉的:
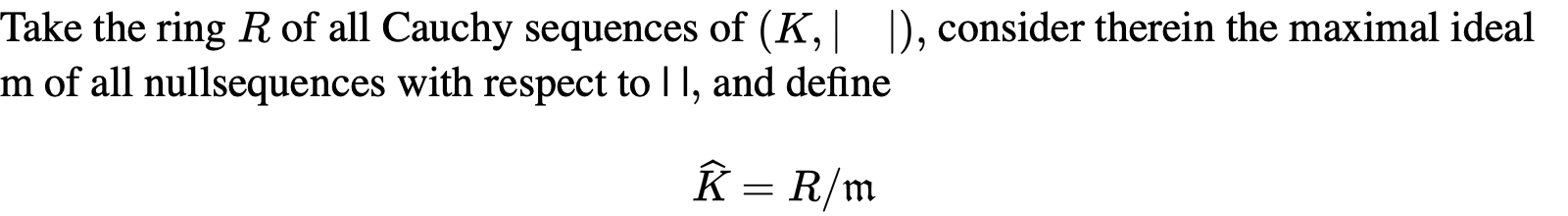
我们可以把原来的域嵌入到完备化后的域中,我们也要考察valuation的变化:
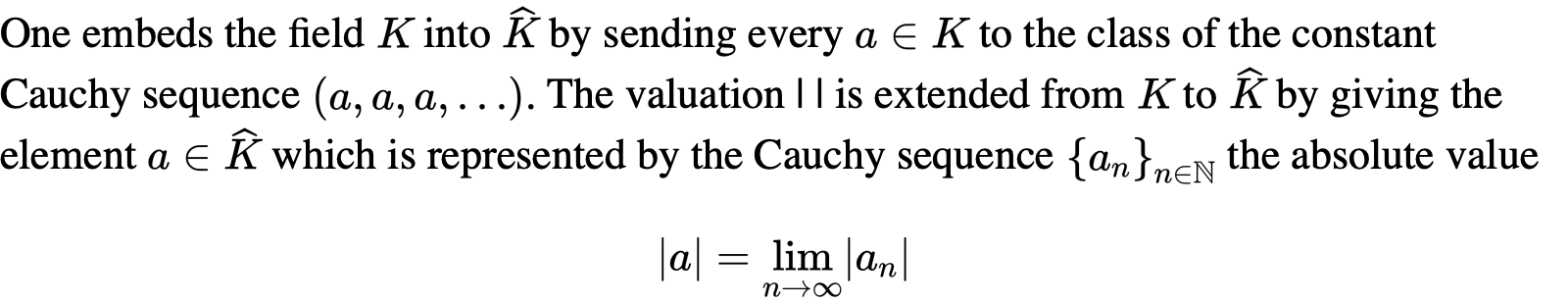

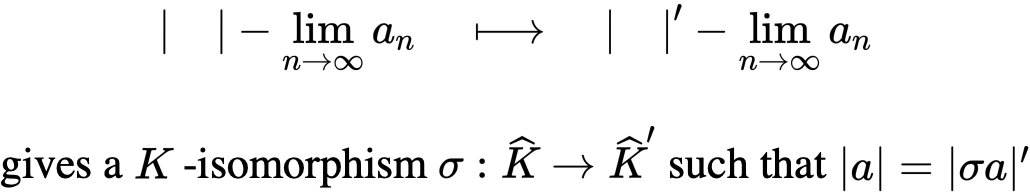
Ostrowski Theorem告诉我们,archimedean valuation下的完备域是确定的:

结论是惊人的,我们重点解析它的证明过程,证明采用反证法,证明的关键在于把问题转化为说明K上的数必然满足R上的一个二次方程:
我们首先说明实数域含于R:

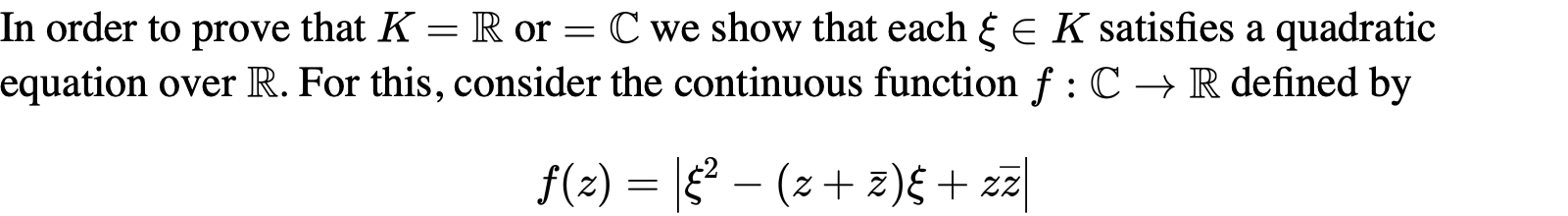
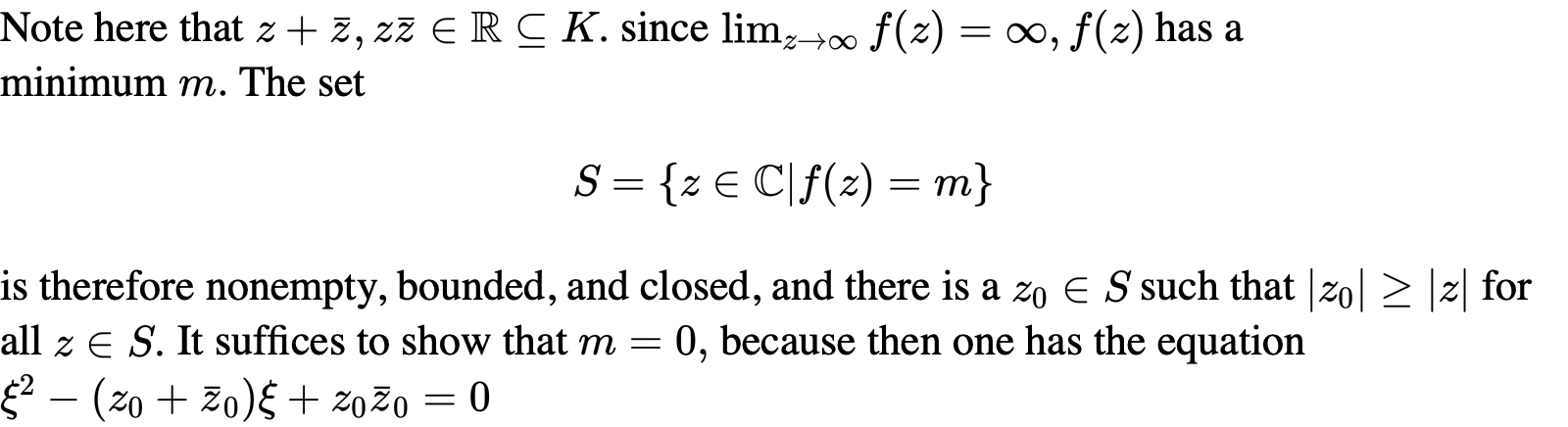


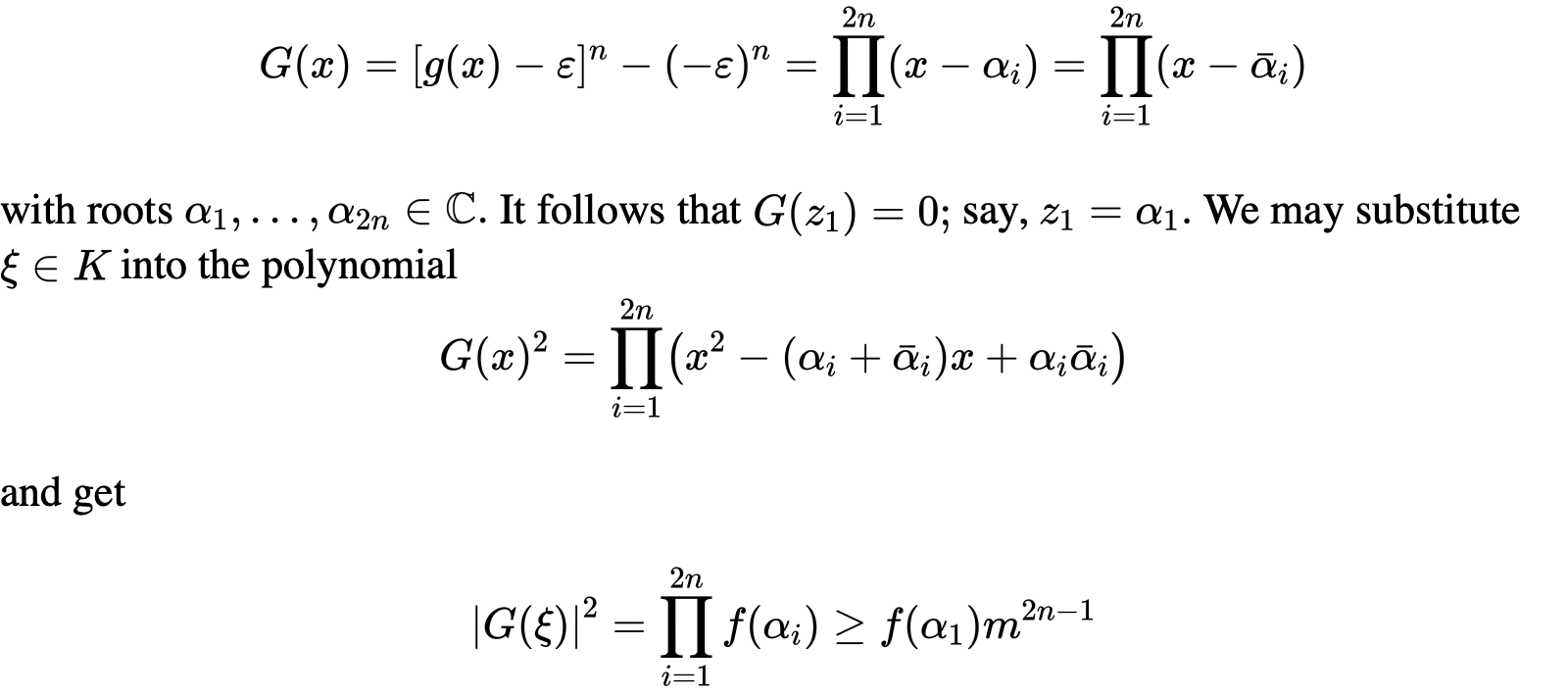

于是我们重点考察nonarchimedan valuation,

以下两个定理不过是p-adic的推广:
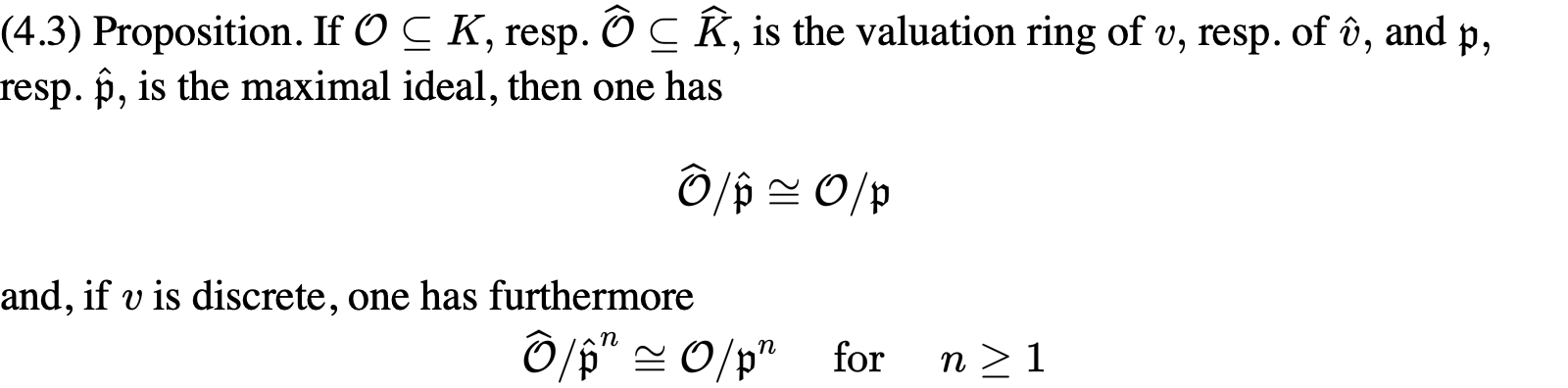

在有理函数域中关于素理想的valuation作完备化得到的是形式幂级数域:

其次,用投影极限也可以用到一般valuation theory的理论中:
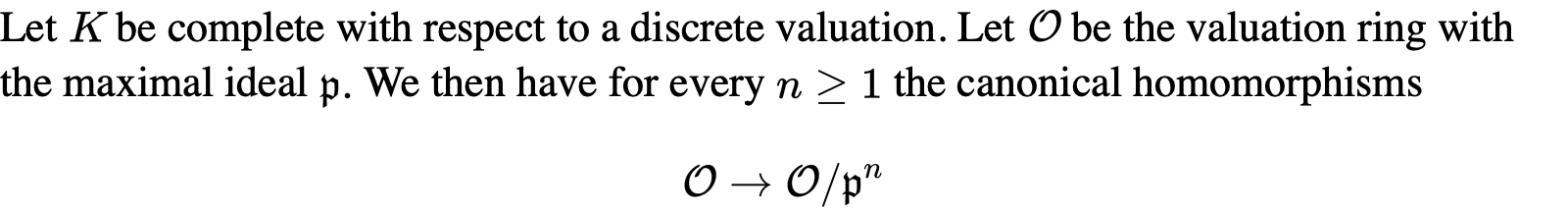
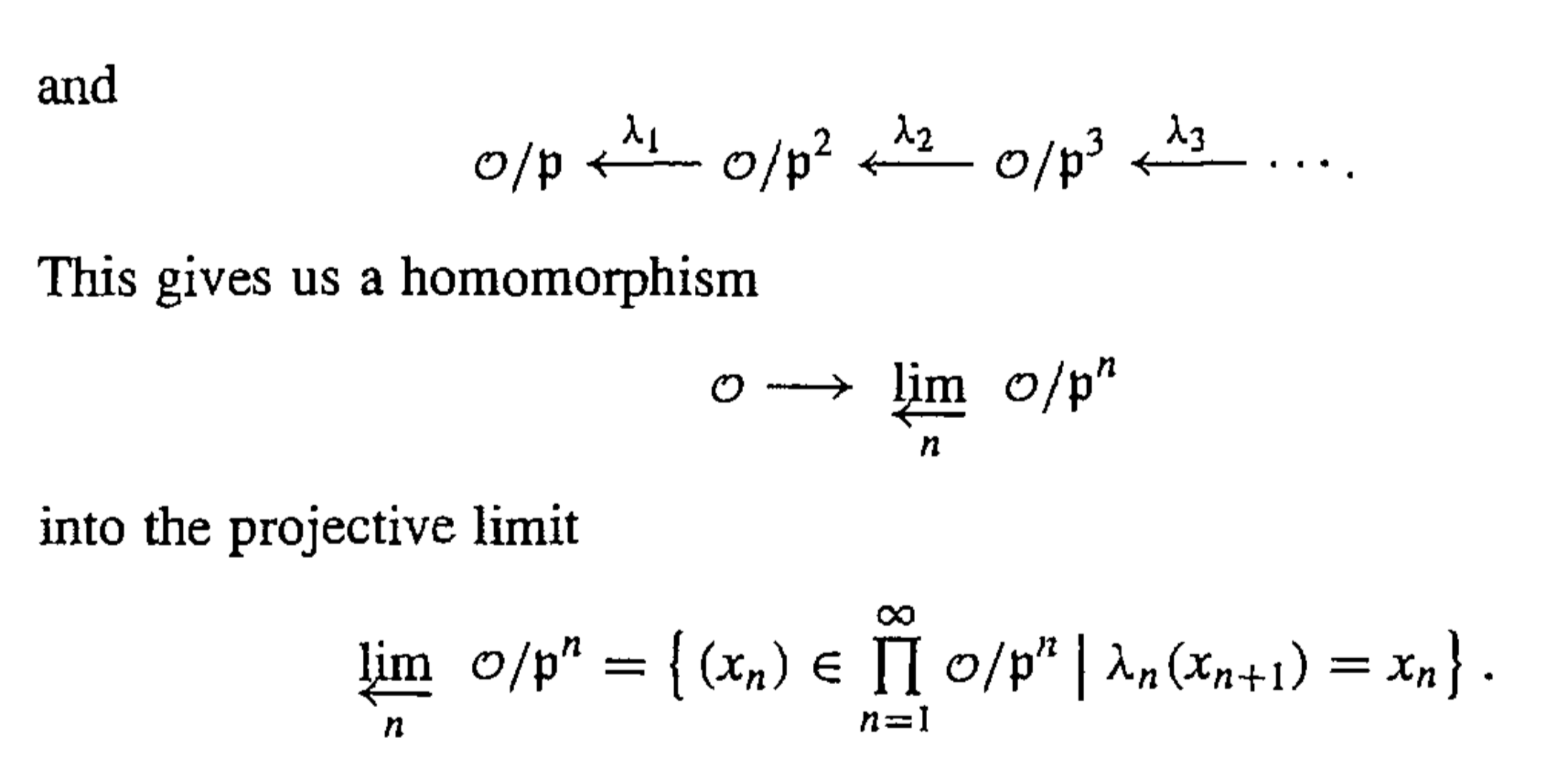



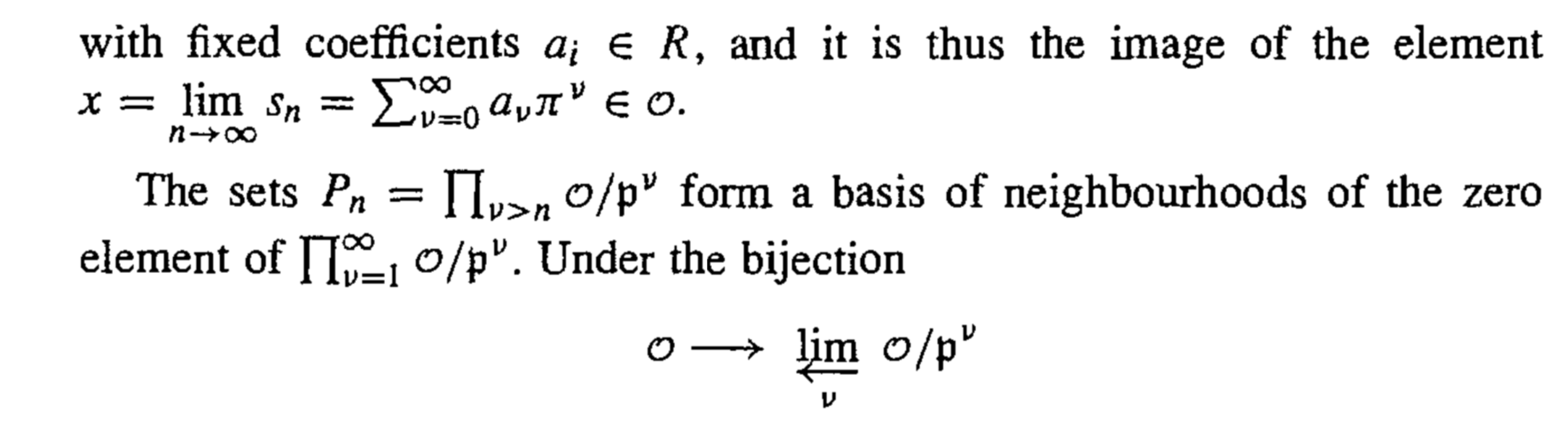

关键的是需要记住两部分的0元素的开邻域基。



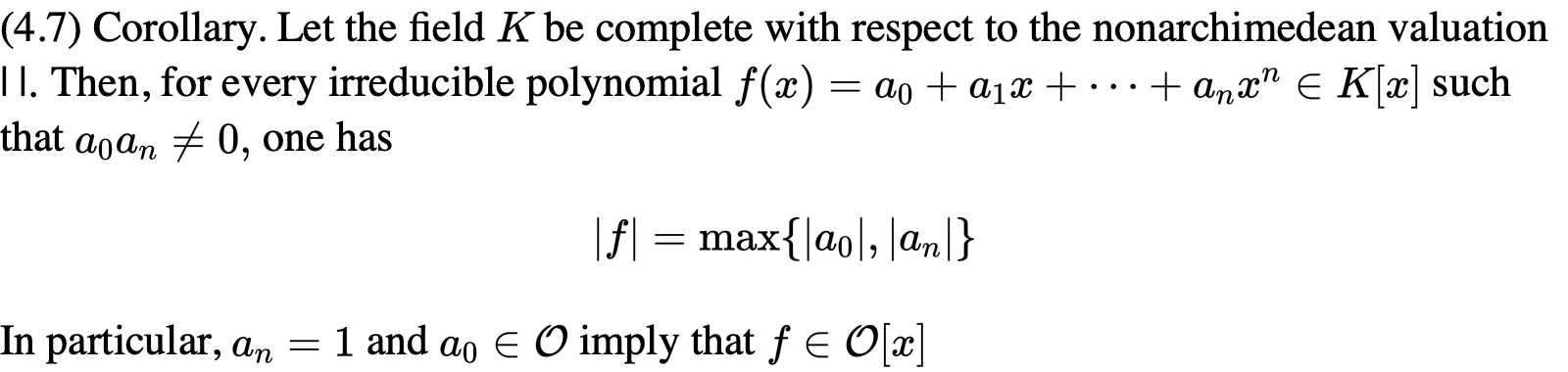

我们把valuation诱导到代数扩张的域上面去:

我们重点解析这一定理的证明:
首先不难讨论Archimedean的情况以及令扩张次数有限:
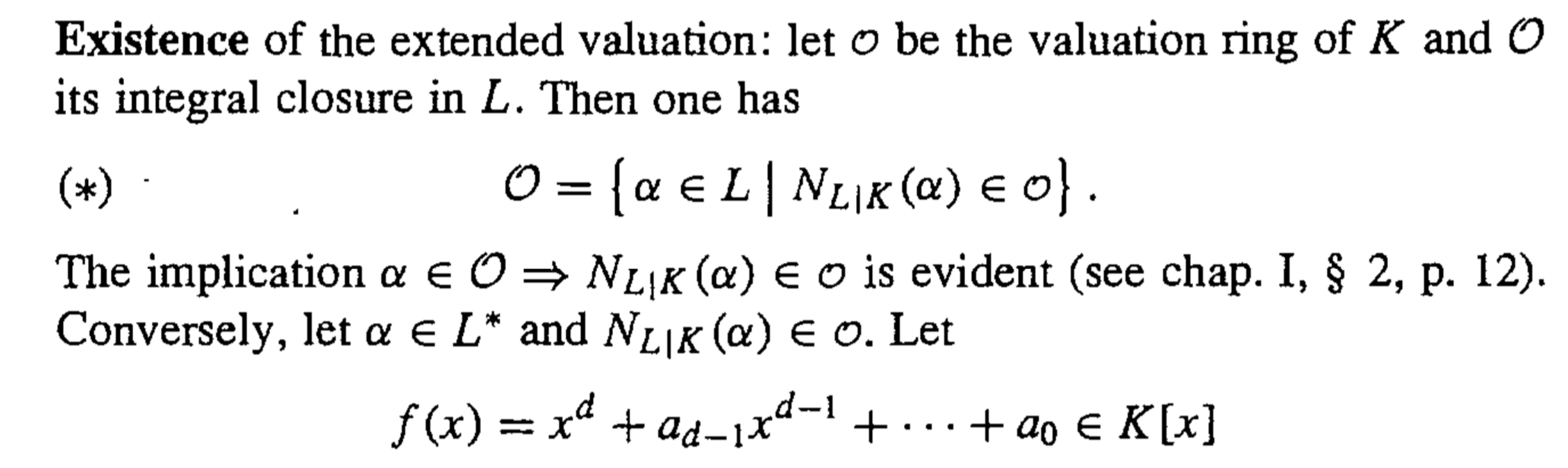
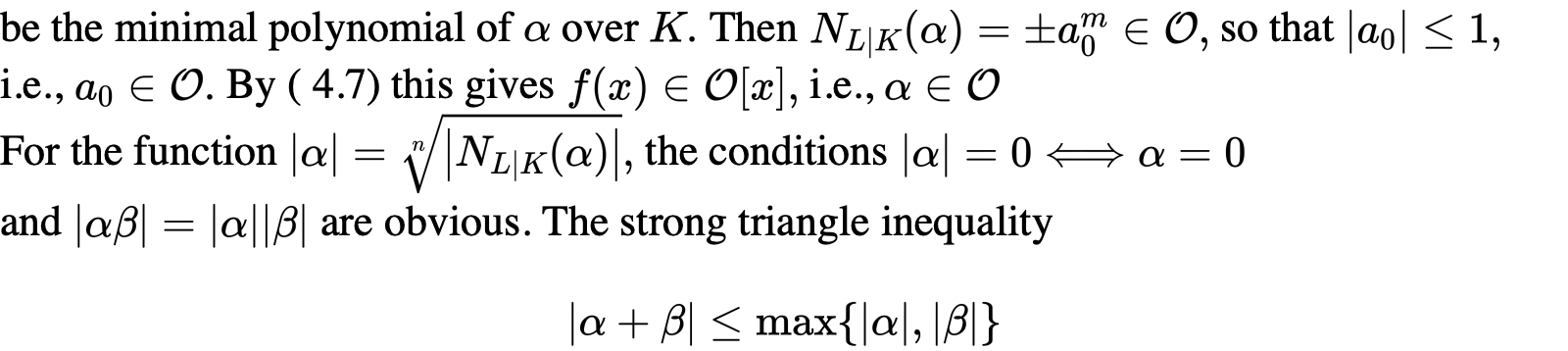


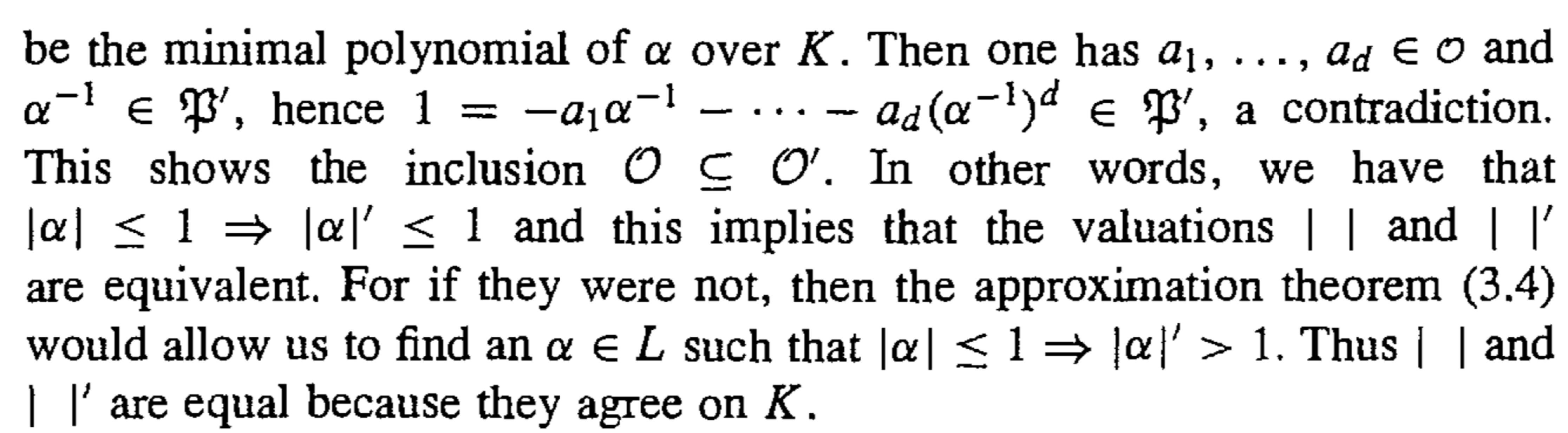



 浙公网安备 33010602011771号
浙公网安备 33010602011771号