第二次大作业blog
前言:
这里是第二次大作业的blog,这次的三道题相较于三次难度又提升了不小,但是由于多边形特点的相似性,在问题的分析和处理上与上一次三角形的有很多相似之处和值得借鉴的地方,但是由于本人的偷懒和死脑筋,三题中也只有两题拿到了满分,算是一次不算太满意的作业。希望下次自己能够继续改进,消除惰性,争取拿到满分。编程方面常识性错误出现的情况少了很多(恭喜我自己)不过还是出现了很多次“又报错?!” 和 “不报错?!”,好在大多数问题都在分析和重新编写下完美解决。
而期中考试的三道题可以说是非常简单了,如果学习了子父类继承和集合知识,很容易就能拿到满分,故在下面的分析中也只给出第三题的分析与解答。
设计与分析:
1.点线形系列4-凸四边形的计算
题目要求:
用户输入一组选项和数据,进行与四边形有关的计算。
以下四边形顶点的坐标要求按顺序依次输入,连续输入的两个顶点是相邻顶点,第一个和最后一个输入的顶点相邻。
选项包括:
1:输入四个点坐标,判断是否是四边形、平行四边形,判断结果输出true/false,结果之间以一个英文空格符分隔。
2:输入四个点坐标,判断是否是菱形、矩形、正方形,判断结果输出true/false,结果之间以一个英文空格符分隔。 若四个点坐标无法构成四边形,输出"not a quadrilateral"
3:输入四个点坐标,判断是凹四边形(false)还是凸四边形(true),输出四边形周长、面积,结果之间以一个英文空格符分隔。 若四个点坐标无法构成四边形,输出"not a quadrilateral"
4:输入六个点坐标,前两个点构成一条直线,后四个点构成一个四边形或三角形,输出直线与四边形(也可能是三角形)相交的交点数量。如果交点有两个,再按面积从小到大输出四边形(或三角形)被直线分割成两部分的面积(不换行)。若直线与四边形或三角形的一条边线重合,输出"The line is coincide with one of the lines"。若后四个点不符合四边形或三角形的输入,输出"not a quadrilateral or triangle"。
后四个点构成三角形的情况:假设三角形一条边上两个端点分别是x、y,边线中间有一点z,另一顶点s:
1)符合要求的输入:顶点重复或者z与xy都相邻,如x x y s、x z y s、x y x s、s x y y。此时去除冗余点,保留一个x、一个y。
2) 不符合要求的输入:z 不与xy都相邻,如z x y s、x z s y、x s z y
5:输入五个点坐标,输出第一个是否在后四个点所构成的四边形(限定为凸四边形,不考虑凹四边形)或三角形(判定方法见选项4)的内部(若是四边形输出in the quadrilateral/outof the quadrilateral,若是三角形输出in the triangle/outof the triangle)。如果点在多边形的某条边上,输出"on the triangle或者on the quadrilateral"。若后四个点不符合四边形或三角形,输出"not a quadrilateral or triangle"。
输入的基本格式为:选项+":"+坐标x+","+坐标y+" "+坐标x+","+坐标y。点的x、y坐标之间以英文","分隔,点与点之间以一个英文空格分隔。
题目分析:
本题涉及到一下几个关键步骤:
1.输入字符串的格式判断及相应处理
我们选择采用正则表达式和String.split方式对输入字符串的格式进行判断,然后再进行拆分和二次判断,最后将处理完的字符串转为相应点坐标(浮点数),应用到后续代码中。
2.四边形的点和边的定义
当处理完输入的字符串后,我们将其分隔为点的坐标,以此构成点对象,再用点对象构成线对象,最后再赋给四边形对象,以此构建一个我们可以分析的四边形模型。
3.四边形构成是否合理的判断
通过输入的点坐标进行判断是否能构成四边形以及其凹凸性。
4.特殊的三角形构成方式
依照题意,首先判断是否存在三点共线的情况,如存在,则判断三点位置以及输入顺序是否合法,若合法则正常操作,若不合法则摒弃。
代码及注释:
package 博客2; import java.math.BigDecimal; import java.util.Scanner; public class 四边形 { public static void main(String[] args) { Scanner sc = new Scanner(System.in); Quadrilateral qua = new Quadrilateral(); Point[] points = new Point[999]; int judge = 1, judge2 = 1;//初始化错误输入判断数 String zz = "^[+-]?(0|(0\\.\\d+)?|[1-9]\\d*(\\.\\d+)?)$";//正则表达式 String input = sc.nextLine();//接收输入 if ((input.charAt(0) != '1' && input.charAt(0) != '2' && input.charAt(0) != '3' && input.charAt(0) != '4' && input.charAt(0) != '5') || input.charAt(1) != ':' /*|| (input.charAt(input.length() - 1) < '0' || input.charAt(input.length() - 1) > '9')*/) judge = 0;//当开头不满足“(1~5):”格式时,给判断数置0 String text = input.substring(2);//去除开头 String[] zmy = text.split(" ");//按照空格分割字符串 for (int z = 0; z < zmy.length; z++) { String[] zsh = zmy[z].split(",");//按照,分割字符串 if (zsh.length != 2) {//当坐标格式不为x,x时即有多余成分(such as: ,,)判断数置0 judge2 = 0; break; } if (!zsh[0].matches(zz) || !zsh[1].matches(zz)) {//当子字符串格式不匹配时,判断数置0 judge2 = 0; break; } Point a = new Point(); points[z] = a; points[z].x = Double.parseDouble(zsh[0]); points[z].y = Double.parseDouble(zsh[1]); } if (judge == 0) {//错误输入1 System.out.print("Wrong Format"); } else if (judge2 == 0) {//错误输入二 System.out.print("Wrong Format"); } else if ((input.charAt(0) == '1' || input.charAt(0) == '2' || input.charAt(0) == '3') && zmy.length != 4 || (input.charAt(0) == '4' && zmy.length != 6) || input.charAt(0) == '5' && zmy.length != 5) { //选项和输入的点的个数不匹配时 System.out.print("wrong number of points"); } else { if (input.charAt(0) == '1') {//1:0,0 0,1 1,1 1,0 String outS1, outS2; qua.setA(points[0]); qua.setB(points[1]); qua.setC(points[2]); qua.setD(points[3]); if (qua.A.collide(qua.B) || qua.A.collide(qua.C) || qua.A.collide(qua.D) || qua.B.collide(qua.C) || qua.B.collide(qua.D) || qua.C.collide(qua.D)) { System.out.print("points coincide"); } else { if (!qua.quadrilateralJudge()) { outS1 = "false"; outS2 = "false"; } else { lineSet(qua); qua.abcSet(); outS1 = "true"; if (qua.parallelogram()) outS2 = "true"; else outS2 = "false"; } System.out.print(outS1 + ' ' + outS2); } } else if (input.charAt(0) == '2') { qua.setA(points[0]); qua.setB(points[1]); qua.setC(points[2]); qua.setD(points[3]); if (!qua.quadrilateralJudge()) { System.out.print("not a quadrilateral"); } else { if (qua.A.collide(qua.B) || qua.A.collide(qua.C) || qua.A.collide(qua.D) || qua.B.collide(qua.C) || qua.B.collide(qua.D) || qua.C.collide(qua.D)) { System.out.print("points coincide"); } else { String outS1, outS2, outS3; lineSet(qua); if (!qua.parallelogram()) { outS1 = "false"; outS2 = "false"; outS3 = "false"; } else { if (qua.Diamond()) { outS1 = "true"; } else outS1 = "false"; if (qua.rectangle()) outS2 = "true"; else outS2 = "false"; if (qua.Diamond() && qua.rectangle()) outS3 = "true"; else outS3 = "false"; } System.out.println(outS1 + " " + outS2 + " " + outS3); } } } else if (input.charAt(0) == '3') { qua.setA(points[0]); qua.setB(points[1]); qua.setC(points[2]); qua.setD(points[3]); if (!qua.quadrilateralJudge()) { System.out.print("not a quadrilateral"); } else { if (qua.A.collide(qua.B) || qua.A.collide(qua.C) || qua.A.collide(qua.D) || qua.B.collide(qua.C) || qua.B.collide(qua.D) || qua.C.collide(qua.D)) { System.out.print("points coincide"); } else { String outS; double area = 0, length = 0; lineSet(qua); qua.abcSet(); Point p = new Point(); p = getDian(qua.AC, qua.BD); length = qua.A.count(qua.B) + qua.B.count(qua.C) + qua.C.count(qua.D) + qua.D.count(qua.A); if (p.count(qua.A) + p.count(qua.C) != qua.A.count(qua.C) && p.count(qua.B) + p.count(qua.D) == qua.B.count(qua.D)) {//凹点在AC之间 outS = "false"; area = qua.AC.lengthCount(qua.B) * 0.5 * qua.A.count(qua.C) + qua.AC.lengthCount(qua.D) * 0.5 * qua.A.count(qua.C); } else if (p.count(qua.A) + p.count(qua.C) == qua.A.count(qua.C) && p.count(qua.B) + p.count(qua.D) != qua.B.count(qua.D)) {//凹点在BD之间 outS = "false"; area = qua.BD.lengthCount(qua.A) * 0.5 * qua.B.count(qua.D) + qua.BD.lengthCount(qua.C) * 0.5 * qua.B.count(qua.D); } else { outS = "true"; area = qua.AC.lengthCount(qua.B) * 0.5 * qua.A.count(qua.C) + qua.AC.lengthCount(qua.D) * 0.5 * qua.A.count(qua.C); } System.out.println(outS + " " + change(length) + " " + change(area)); } } } else if (input.charAt(0) == '4') {//4:1,0 10,0 0,0 0,10 0,80 20,30 Point p1 = new Point(); Point p2 = new Point(); p1 = points[0]; p2 = points[1]; qua.setA(points[2]); qua.setB(points[3]); qua.setC(points[4]); qua.setD(points[5]); if (p1.collide(p2)) { System.out.print("points coincide"); } else { lineSet(qua); Line x = new Line(points[0], points[1]); x.abcCount(points[0], points[1]); int tMark = 0; int oMark = 1; Triangle triangle = new Triangle(); Line l1 = new Line(qua.A, qua.C); Line l2 = new Line(qua.B, qua.D); l1.abcCount(qua.A, qua.C);//线AC l2.abcCount(qua.B, qua.D);//线BD if (points[2].collide(points[3]) ||//AB重合 points[3].collide(points[4]) ||//CB重合 points[3].collide(points[5])) {//DB重合//去掉点B 三角形ACD Triangle tria = new Triangle(qua.A, qua.C, qua.D); if (!tria.triangleJudge(tria.A, tria.B, tria.C) || tria.A.collide(tria.B) || tria.A.collide(tria.C) || tria.B.collide(tria.C)) System.out.print("not a quadrilateral or triangle"); else { tria.x1 = new Line(tria.A, tria.B); tria.x2 = new Line(tria.A, tria.C); tria.x3 = new Line(tria.B, tria.C); tria.abcCount(); triangle = tria; tMark = 1; } } else if (points[2].collide(points[4]) ||//AC重合 points[5].collide(points[4])//DC重合 ) {//三角形ABD Triangle tria = new Triangle(qua.A, qua.B, qua.D); if (!tria.triangleJudge(tria.A, tria.B, tria.C) || tria.A.collide(tria.B) || tria.A.collide(tria.C) || tria.B.collide(tria.C)) System.out.print("not a quadrilateral or triangle"); else { tria.x1 = new Line(tria.A, tria.B); tria.x2 = new Line(tria.A, tria.C); tria.x3 = new Line(tria.B, tria.C); tria.abcCount(); tMark = 1; triangle = tria; } }//4:10,20 0,20 0,10 0,0 0,80 30,20 else if (points[2].collide(points[5])) {//AD重合//三角形abc Triangle tria = new Triangle(qua.A, qua.B, qua.C); if (!tria.triangleJudge(tria.A, tria.B, tria.C) || tria.A.collide(tria.B) || tria.A.collide(tria.C) || tria.B.collide(tria.C)) System.out.print("not a quadrilateral or triangle"); else { tria.x1 = new Line(tria.A, tria.B); tria.x2 = new Line(tria.A, tria.C); tria.x3 = new Line(tria.B, tria.C); tria.abcCount(); tMark = 1; } } else if (points[3].x * l1.A + points[3].y * l1.B + l1.C == 0)//B 在线AC上 { if (!((qua.B.x > Math.min(qua.A.x, qua.C.x) && qua.B.x < Math.max(qua.A.x, qua.C.x)) || (qua.B.y > Math.min(qua.A.y, qua.C.y) && qua.B.y < Math.max(qua.A.y, qua.C.y)) )) { System.out.print("not a quadrilateral or triangle"); oMark = 0; } else { Triangle tria = new Triangle(qua.A, qua.C, qua.D); if (!tria.triangleJudge(tria.A, tria.B, tria.C) || tria.A.collide(tria.B) || tria.A.collide(tria.C) || tria.B.collide(tria.C)) System.out.print("not a quadrilateral or triangle"); else { tria.x1 = new Line(tria.A, tria.B); tria.x2 = new Line(tria.A, tria.C); tria.x3 = new Line(tria.B, tria.C); tria.abcCount(); tMark = 1; triangle = tria; } } } else if (qua.D.x * l1.A + qua.D.y * l1.B + l1.C == 0)//D 在线CA上 { if (!((qua.D.x > Math.min(qua.A.x, qua.C.x) && qua.D.x < Math.max(qua.A.x, qua.C.x)) || (qua.D.y > Math.min(qua.A.y, qua.C.y) && qua.D.y < Math.max(qua.A.y, qua.C.y)) )) { System.out.print("not a quadrilateral or triangle"); oMark = 0; } else { Triangle tria = new Triangle(qua.A, qua.B, qua.C); if (!tria.triangleJudge(tria.A, tria.B, tria.C) || tria.A.collide(tria.B) || tria.A.collide(tria.C) || tria.B.collide(tria.C)) System.out.print("not a quadrilateral or triangle"); else { tria.x1 = new Line(tria.A, tria.B); tria.x2 = new Line(tria.A, tria.C); tria.x3 = new Line(tria.B, tria.C); tria.abcCount(); tMark = 1; triangle = tria; } } } else if (qua.C.x * l2.A + qua.C.y * l2.B + l2.C == 0)//C 在线BD上 { if (!((qua.C.x > Math.min(qua.B.x, qua.D.x) && qua.C.x < Math.max(qua.B.x, qua.D.x)) || (qua.C.y > Math.min(qua.B.y, qua.D.y) && qua.C.y < Math.max(qua.B.y, qua.D.y)) )) { System.out.print("not a quadrilateral or triangle"); oMark = 0; } else { Triangle tria = new Triangle(qua.A, qua.B, qua.D); if (!tria.triangleJudge(tria.A, tria.B, tria.C) || tria.A.collide(tria.B) || tria.A.collide(tria.C) || tria.B.collide(tria.C)) System.out.print("not a quadrilateral or triangle"); else { tria.x1 = new Line(tria.A, tria.B); tria.x2 = new Line(tria.A, tria.C); tria.x3 = new Line(tria.B, tria.C); tria.abcCount(); tMark = 1; triangle = tria; } } } else if (qua.A.x * l2.A + qua.A.y * l2.B + l2.C == 0)////A 在线DB上 { if (!((qua.A.x > Math.min(qua.B.x, qua.D.x) && qua.A.x < Math.max(qua.B.x, qua.D.x)) || (qua.A.y > Math.min(qua.B.y, qua.D.y) && qua.A.y < Math.max(qua.B.y, qua.D.y)) )) { System.out.print("not a quadrilateral or triangle"); oMark = 0; } else { Triangle tria = new Triangle(qua.B, qua.C, qua.D); if (!tria.triangleJudge(tria.A, tria.B, tria.C) || tria.A.collide(tria.B) || tria.A.collide(tria.C) || tria.B.collide(tria.C)) System.out.print("not a quadrilateral or triangle"); else { tria.x1 = new Line(tria.A, tria.B); tria.x2 = new Line(tria.A, tria.C); tria.x3 = new Line(tria.B, tria.C); tria.abcCount(); tMark = 1; triangle = tria; } } } if (oMark == 1) { if (tMark == 1) {//直线与三角形4:10,20 0,20 0,10 0,0 30,20 0,80 triangle.areaCount(triangle, x); } else {//直线与四边形 if (!qua.quadrilateralJudge() || qua.A.collide(qua.B) || qua.A.collide(qua.C) || qua.A.collide(qua.D) || qua.B.collide(qua.C) || qua.B.collide(qua.D) || qua.C.collide(qua.D)) System.out.print("not a quadrilateral or triangle"); else {//构成四边形且有两个交点时 if ((x.A*qua.A.x+ x.B*qua.A.y+x.C==0||x.A*qua.C.x+x.B*qua.C.y+x.C==0)&& (x.A*qua.B.x+x.B*qua.B.y+x.C==0||x.A*qua.D.x+x.B*qua.D.y+x.C==0) ) System.out.print("The line is coincide with one of the lines"); else {//Line x = new Line(points[0], points[1]); Point point1; Point point2;//4:0,0 10,10 0,0 8,0 10,10 2,10 if (!(pointOnLine(getDian(x,qua.AB),qua.AB))&&qua.A.x*x.A+qua.A.y*x.B+x.C!=0 &&!(pointOnLine(getDian(x,qua.BC),qua.BC))&&qua.B.x*x.A+qua.B.y*x.B+x.C!=0 &&!(pointOnLine(getDian(x,qua.CD),qua.CD))&&qua.C.x*x.A+qua.C.y*x.B+x.C!=0 &&!(pointOnLine(getDian(x,qua.DA),qua.DA))&&qua.D.x*x.A+qua.D.y*x.B+x.C!=0) { System.out.print("0"); System.out.println(getDian(x,qua.CD)!=qua.C); } else if (x.A*qua.A.x+x.B*qua.A.y+x.C==0&&!pointOnLine(getDian(x,qua.BC),qua.BC)&&!pointOnLine(getDian(x,qua.CD),qua.CD)&&qua.C.x*x.A+qua.C.y*x.B+x.C!=0) System.out.print("1");//过A点且与BC,CD的交点不在其上,则表明只过点A else if (x.A*qua.B.x+x.B*qua.B.y+x.C==0&&!pointOnLine(getDian(x,qua.DA),qua.DA)&&!pointOnLine(getDian(x,qua.CD),qua.CD)&&qua.D.x*x.A+qua.D.y*x.B+x.C!=0) System.out.print("1");//过B点且与CD,DA的交点不在其上,则表明只过点B else if (x.A*qua.C.x+x.B*qua.C.y+x.C==0&&!pointOnLine(getDian(x,qua.DA),qua.DA)&&!pointOnLine(getDian(x,qua.AB),qua.AB)&&qua.A.x*x.A+qua.A.y*x.B+x.C!=0) System.out.print("1");//过C点且与AB,DA的交点不在其上,则表明只过点C else if (x.A*qua.D.x+x.B*qua.D.y+x.C==0&&!pointOnLine(getDian(x,qua.BC),qua.BC)&&!pointOnLine(getDian(x,qua.AB),qua.AB)&&qua.B.x*x.A+qua.B.y*x.B+x.C!=0) System.out.print("1");//过D点且与AB,BC的交点不在其上,则表明只过点D else { double area,outArea1,outArea2; area = 0.5*qua.AC.lengthCount(qua.D)*qua.A.count(qua.C)+0.5*qua.AC.lengthCount(qua.B)*qua.A.count(qua.C); if (x.A*qua.A.x+x.B*qua.A.y+x.C==0){ countT4(x,qua,area,qua.A,qua.BC,qua.CD,qua.AC,qua.B,qua.D,qua.C); } else if (x.A*qua.B.x+x.B*qua.B.y+x.C==0){ countT4(x,qua,area,qua.B,qua.CD,qua.DA,qua.BD,qua.C,qua.A,qua.D); } else if (x.A*qua.C.x+x.B*qua.C.y+x.C==0){ countT4(x,qua,area,qua.C,qua.DA,qua.AB,qua.AC,qua.D,qua.B,qua.A); } else if (x.A*qua.D.x+x.B*qua.D.y+x.C==0){ countT4(x,qua,area,qua.D,qua.AB,qua.BC,qua.BD,qua.A,qua.C,qua.B); } else {//4:0,4 10,6 0,0 10,0 10,10 0,10 if (pointOnLine(getDian(x,qua.DA),qua.DA)&&pointOnLine(getDian(x,qua.AB),qua.AB)) { countT4Round2(x, qua, qua.DA, qua.AB, getDian(x, qua.DA), getDian(x, qua.AB), area); } else if (pointOnLine(getDian(x,qua.AB),qua.AB)&&pointOnLine(getDian(x,qua.BC),qua.BC)) { countT4Round2(x, qua, qua.AB, qua.BC, getDian(x, qua.AB), getDian(x, qua.BC), area); } else if (pointOnLine(getDian(x,qua.BC),qua.BC)&&pointOnLine(getDian(x,qua.CD),qua.CD)) { countT4Round2(x, qua, qua.BC, qua.CD, getDian(x, qua.BC), getDian(x, qua.CD), area); } else if (pointOnLine(getDian(x,qua.CD),qua.CD)&&pointOnLine(getDian(x,qua.DA),qua.DA)) { System.out.println(getDian(x, qua.CD).x); System.out.println(getDian(x, qua.CD).y); countT4Round2(x, qua, qua.CD, qua.DA, getDian(x, qua.CD), getDian(x, qua.DA), area); } else {//4:0,4 10,6 0,0 10,0 10,10 0,10 if (pointOnLine(getDian(x,qua.DA),qua.DA)&&pointOnLine(getDian(x,qua.BC),qua.BC)) countT4Round3(qua,getDian(x,qua.DA),getDian(x,qua.BC),qua.DA,qua.BC,area); else if(pointOnLine(getDian(x,qua.AB),qua.AB)&&pointOnLine(getDian(x,qua.CD),qua.CD)) { //4:0,2 -2,0 0,0 -10,10 0,20 10,10 countT4Round3(qua, getDian(x, qua.AB), getDian(x, qua.CD), qua.AB, qua.CD, area); } } } } } } } } } } else {//情况5 Point d = new Point(); lineSet(qua); d = points[0]; int tMark = 0; int oMark = 1; qua.setA(points[1]); qua.setB(points[2]); qua.setC(points[3]); qua.setD(points[4]); Triangle triangle = new Triangle(); Line l1 = new Line(qua.A, qua.C); Line l2 = new Line(qua.B, qua.D); l1.abcCount(qua.A, qua.C);//线AC l2.abcCount(qua.B, qua.D);//线BD if (points[1].collide(points[2]) ||//AB重合 points[2].collide(points[3]) ||//CB重合 points[2].collide(points[4])) {//DB重合//去掉点B 三角形ACD Triangle tria = new Triangle(qua.A, qua.C, qua.D); if (!tria.triangleJudge(tria.A, tria.B, tria.C) || tria.A.collide(tria.B) || tria.A.collide(tria.C) || tria.B.collide(tria.C)) System.out.print("not a quadrilateral or triangle"); else { tria.x1 = new Line(tria.A, tria.B); tria.x2 = new Line(tria.A, tria.C); tria.x3 = new Line(tria.B, tria.C); tria.abcCount(); triangle = tria; tMark = 1; } } else if (points[1].collide(points[3]) ||//AC重合 points[4].collide(points[3])//DC重合 ) {//三角形ABD Triangle tria = new Triangle(qua.A, qua.B, qua.D); if (!tria.triangleJudge(tria.A, tria.B, tria.C) || tria.A.collide(tria.B) || tria.A.collide(tria.C) || tria.B.collide(tria.C)) System.out.print("not a quadrilateral or triangle"); else { tria.x1 = new Line(tria.A, tria.B); tria.x2 = new Line(tria.A, tria.C); tria.x3 = new Line(tria.B, tria.C); tria.abcCount(); tMark = 1; triangle = tria; } }//4:10,20 0,20 0,10 0,0 0,80 30,20 else if (points[1].collide(points[4])) {//AD重合//三角形abc Triangle tria = new Triangle(qua.A, qua.B, qua.C); if (!tria.triangleJudge(tria.A, tria.B, tria.C) || tria.A.collide(tria.B) || tria.A.collide(tria.C) || tria.B.collide(tria.C)) System.out.print("not a quadrilateral or triangle"); else { tria.x1 = new Line(tria.A, tria.B); tria.x2 = new Line(tria.A, tria.C); tria.x3 = new Line(tria.B, tria.C); tria.abcCount(); tMark = 1; triangle = tria; } } else if (points[2].x * l1.A + points[2].y * l1.B + l1.C == 0)//B 在线AC上 { if (!((qua.B.x > Math.min(qua.A.x, qua.C.x) && qua.B.x < Math.max(qua.A.x, qua.C.x)) || (qua.B.y > Math.min(qua.A.y, qua.C.y) && qua.B.y < Math.max(qua.A.y, qua.C.y)) )) { System.out.print("not a quadrilateral or triangle"); oMark = 0; } else { Triangle tria = new Triangle(qua.A, qua.C, qua.D); if (!tria.triangleJudge(tria.A, tria.B, tria.C) || tria.A.collide(tria.B) || tria.A.collide(tria.C) || tria.B.collide(tria.C)) System.out.print("not a quadrilateral or triangle"); else { tria.x1 = new Line(tria.A, tria.B); tria.x2 = new Line(tria.A, tria.C); tria.x3 = new Line(tria.B, tria.C); tria.abcCount(); tMark = 1; triangle = tria; } } } else if (qua.D.x * l1.A + qua.D.y * l1.B + l1.C == 0)//D 在线CA上 { if (!((qua.D.x > Math.min(qua.A.x, qua.C.x) && qua.D.x < Math.max(qua.A.x, qua.C.x)) || (qua.D.y > Math.min(qua.A.y, qua.C.y) && qua.D.y < Math.max(qua.A.y, qua.C.y)) )) { System.out.print("not a quadrilateral or triangle"); oMark = 0; } else { Triangle tria = new Triangle(qua.A, qua.B, qua.C); if (!tria.triangleJudge(tria.A, tria.B, tria.C) || tria.A.collide(tria.B) || tria.A.collide(tria.C) || tria.B.collide(tria.C)) System.out.print("not a quadrilateral or triangle"); else { tria.x1 = new Line(tria.A, tria.B); tria.x2 = new Line(tria.A, tria.C); tria.x3 = new Line(tria.B, tria.C); tria.abcCount(); tMark = 1; triangle = tria; } } } else if (qua.C.x * l2.A + qua.C.y * l2.B + l2.C == 0)//C 在线BD上 { if (!((qua.C.x > Math.min(qua.B.x, qua.D.x) && qua.C.x < Math.max(qua.B.x, qua.D.x)) || (qua.C.y > Math.min(qua.B.y, qua.D.y) && qua.C.y < Math.max(qua.B.y, qua.D.y)) )) { System.out.print("not a quadrilateral or triangle"); oMark = 0; } else { Triangle tria = new Triangle(qua.A, qua.B, qua.D); if (!tria.triangleJudge(tria.A, tria.B, tria.C) || tria.A.collide(tria.B) || tria.A.collide(tria.C) || tria.B.collide(tria.C)) System.out.print("not a quadrilateral or triangle"); else { tria.x1 = new Line(tria.A, tria.B); tria.x2 = new Line(tria.A, tria.C); tria.x3 = new Line(tria.B, tria.C); tria.abcCount(); tMark = 1; triangle = tria; } } } else if (qua.A.x * l2.A + qua.A.y * l2.B + l2.C == 0)////A 在线DB上 { if (!((qua.A.x > Math.min(qua.B.x, qua.D.x) && qua.A.x < Math.max(qua.B.x, qua.D.x)) || (qua.A.y > Math.min(qua.B.y, qua.D.y) && qua.A.y < Math.max(qua.B.y, qua.D.y)) )) { System.out.print("not a quadrilateral or triangle"); oMark = 0; } else { Triangle tria = new Triangle(qua.B, qua.C, qua.D); if (!tria.triangleJudge(tria.A, tria.B, tria.C) || tria.A.collide(tria.B) || tria.A.collide(tria.C) || tria.B.collide(tria.C)) System.out.print("not a quadrilateral or triangle"); else { tria.x1 = new Line(tria.A, tria.B); tria.x2 = new Line(tria.A, tria.C); tria.x3 = new Line(tria.B, tria.C); tria.abcCount(); tMark = 1; triangle = tria; } } } if (oMark == 1) { if (tMark == 1) {//直线与三角形4:10,20 0,20 0,10 0,0 30,20 0,80 double tArea = Math.sqrt(Math.pow(triangle.A.x - triangle.B.x, 2) + Math.pow(triangle.A.y - triangle.B.y, 2)) * triangle.x1.lengthCount(triangle.C) / 2; //计算总面积 if (triangle.x1.A * d.x + triangle.x1.B * d.y + triangle.x1.C == 0 || triangle.x2.A * d.x + triangle.x2.B * d.y + triangle.x2.C == 0 || triangle.x3.A * d.x + triangle.x3.B * d.y + triangle.x3.C == 0) System.out.print("on the triangle");//点在任意一条边上时 else { double L1, L2, L3; double x1, x2, x3; L1 = triangle.x1.lengthCount(d);//计算三条边的长度 L2 = triangle.x2.lengthCount(d); L3 = triangle.x3.lengthCount(d); x1 = Math.sqrt(Math.pow(triangle.A.x - triangle.B.x, 2) + Math.pow(triangle.A.y - triangle.B.y, 2));//计算点和任意两顶点构成三角形的面积 x2 = Math.sqrt(Math.pow(triangle.A.x - triangle.C.x, 2) + Math.pow(triangle.A.y - triangle.C.y, 2)); x3 = Math.sqrt(Math.pow(triangle.C.x - triangle.B.x, 2) + Math.pow(triangle.C.y - triangle.B.y, 2)); if (Math.sqrt((L1 * x1 + L2 * x2 + L3 * x3) / 2 - tArea) < 0.0001)//当三个面积相加刚好等于三角形面积时。则点在三角形内 System.out.print("in the triangle"); else System.out.print("outof the triangle"); } } else{//直线与四边形 if (!qua.quadrilateralJudge() || qua.A.collide(qua.B) || qua.A.collide(qua.C) || qua.A.collide(qua.D) || qua.B.collide(qua.C) || qua.B.collide(qua.D) || qua.C.collide(qua.D)) System.out.print("not a quadrilateral or triangle"); else { if (d.collide(qua.A)||d.collide(qua.B)||d.collide(qua.C)||d.collide(qua.D)){ System.out.print("on the quadrilateral"); } else if ((qua.AB.A*d.x+qua.AB.B*d.y+qua.AB.C==0&&((d.x>Math.min(qua.A.x,qua.B.x)&&d.x<Math.max(qua.A.x,qua.B.x))||(d.y>Math.min(qua.A.y,qua.B.y)&&d.y<Math.max(qua.A.y,qua.B.y))))|| (qua.BC.A*d.x+qua.BC.B*d.y+qua.BC.C==0&&((d.x>Math.min(qua.C.x,qua.B.x)&&d.x<Math.max(qua.C.x,qua.B.x))||(d.y>Math.min(qua.C.y,qua.B.y)&&d.y<Math.max(qua.C.y,qua.B.y))))|| (qua.CD.A*d.x+qua.CD.B*d.y+qua.CD.C==0&&((d.x>Math.min(qua.C.x,qua.D.x)&&d.x<Math.max(qua.C.x,qua.D.x))||(d.y>Math.min(qua.C.y,qua.D.y)&&d.y<Math.max(qua.C.y,qua.D.y))))|| (qua.DA.A*d.x+qua.DA.B*d.y+qua.DA.C==0&&((d.x>Math.min(qua.A.x,qua.D.x)&&d.x<Math.max(qua.A.x,qua.D.x))||(d.y>Math.min(qua.A.y,qua.D.y)&&d.y<Math.max(qua.A.y,qua.D.y)))) ) { System.out.print("on the quadrilateral"); } else{ double area; //5:2.88,6.29 0,14 -10,4 0,0 10,5 area = 0.5*qua.AC.lengthCount(qua.D)*qua.A.count(qua.C)+0.5*qua.AC.lengthCount(qua.B)*qua.A.count(qua.C); double area2; area2 = 0.5*qua.AB.lengthCount(d)*qua.A.count(qua.B) + 0.5*qua.BC.lengthCount(d)*qua.C.count(qua.B) + 0.5*qua.CD.lengthCount(d)*qua.C.count(qua.D) + 0.5*qua.DA.lengthCount(d)*qua.D.count(qua.A); if (Math.abs(area2-area)>0.00000000001) System.out.println("outof the quadrilateral"); else System.out.println("in the quadrilateral");//5:11,10 0,0 10,10 0,20 -10,10 } } } } } } } public static void countT4(Line x , Quadrilateral qua , double area , Point point , Line l1, Line l2 , Line l3 , Point p1, Point p2 , Point p3){ Point point1 = new Point(); Point point2 = new Point(); double outArea1,outArea2; point1 = point; if (pointOnLine(getDian(x,l1),l1)){//过该点和对边 point2 = getDian(x,l1); outArea1 = 0.5*x.lengthCount(p1)*point1.count(point2); outArea2 = area - outArea1; if (outArea1>outArea2) System.out.println("2 "+change(outArea2)+" "+change(outArea1)); else System.out.println("2 "+change(outArea1)+" "+change(outArea2)); } else if (x.A*p3.x+x.B*p3.y+x.C==0){//过该点和该点相对的点 point2 = p3; outArea1 = 0.5*l3.lengthCount(p1)*point.count(p3); outArea2 = 0.5*l3.lengthCount(p2)*point.count(p3); if (outArea1>outArea2) System.out.println("2 "+change(outArea2)+" "+change(outArea1)); else System.out.println("2 "+change(outArea1)+" "+change(outArea2)); } else{//过该点和对边 point2 = getDian(x,l2); outArea1 = 0.5*x.lengthCount(p2)*point1.count(point2); outArea2 = area - outArea1; if (outArea1>outArea2) System.out.println("2 "+change(outArea2)+" "+change(outArea1)); else System.out.println("2 "+change(outArea1)+" "+change(outArea2)); } } public static void countT4Round2(Line x ,Quadrilateral qua , Line l1 , Line l2 , Point p1 , Point p2 , double area){ Point p = new Point(); if (l1==qua.DA&&l2==qua.AB) p = qua.A; else if (l1==qua.AB&&l2==qua.BC) p = qua.B; else if (l1==qua.BC&&l2==qua.CD) p = qua.C; else p = qua.D; double outArea1,outArea2; outArea1 = 0.5*x.lengthCount(p)* p1.count(p2); outArea2 = area - outArea1; if (outArea1>outArea2) System.out.println("2 "+change(outArea2)+" "+change(outArea1)); else System.out.println("2 "+change(outArea1)+" "+change(outArea2)); } public static void countT4Round3(Quadrilateral qua , Point p1 , Point p2 , Line l1 , Line l2 , double area){ Point point1 = new Point(); Point point2 = new Point(); double outArea1,outArea2; if (l1==qua.DA&&l2==qua.BC){ point1 = qua.A; point2 = qua.B; } else { point1 = qua.B; point2 = qua.C; } Line l = new Line(point1,p2); l.abcCount(point1,p2); outArea1 = 0.5*(l.lengthCount(point2)*point1.count(p2)+l.lengthCount(p1)*point1.count(p2)); outArea2 = area - outArea1; if (outArea1>outArea2) System.out.println("2 "+change(outArea2)+" "+change(outArea1)); else System.out.println("2 "+change(outArea1)+" "+change(outArea2)); } public static double change(double d) {//转化为三位小数 double d1; BigDecimal big = new BigDecimal(d); d1 = big.setScale(3, BigDecimal.ROUND_HALF_UP).doubleValue(); return d1; } public static Point getDian(Line x, Line y) {//计算交点 Point re = new Point(); re.x = (y.C * x.B - x.C * y.B) / (x.A * y.B - y.A * x.B); re.y = (x.C * y.A - y.C * x.A) / (x.A * y.B - y.A * x.B); return re; } public static void lineSet(Quadrilateral qua) {//初始化四边形各边 qua.AB = new Line(qua.A, qua.B); qua.BC = new Line(qua.B, qua.C); qua.CD = new Line(qua.C, qua.D); qua.DA = new Line(qua.D, qua.A); qua.AC = new Line(qua.A, qua.C); qua.BD = new Line(qua.B, qua.D); } public static boolean pointOnLine(Point p,Line l ){ if (l.A==0){ if ((p.x>Math.min(l.zmy[0].x,l.zmy[1].x)&&p.x<Math.max(l.zmy[0].x,l.zmy[1].x))) return true; else return false; } else if (l.B==0){ if ((p.y>Math.min(l.zmy[0].y,l.zmy[1].y)&&p.x<Math.max(l.zmy[0].y,l.zmy[1].y))) return true; else return false; } if((p.x>Math.min(l.zmy[0].x,l.zmy[1].x)&&p.x<Math.max(l.zmy[0].x,l.zmy[1].x))||(p.y>Math.min(l.zmy[0].y,l.zmy[1].y)&&p.x<Math.max(l.zmy[0].y,l.zmy[1].y))) return true;//点在线段上 else return false; } } class Point { double x, y; public Point() { } public double count(Point a) {//求两点之间距离 double fin; fin = Math.sqrt(Math.pow((a.x - this.x), 2) + Math.pow((a.y - this.y), 2)); return fin; } boolean collide(Point b) {//求重合点 if (this.x == b.x && this.y == b.y) return true; else return false; } } class Line { Point[] zmy = new Point[2]; double A, B, C; public Line() { } public Line(Point a, Point b) { zmy[0] = a; zmy[1] = b; } double slope(Point a, Point b) {//求斜率 double sSlope; if (b.x == a.x) sSlope = 1000000000; else { sSlope = (b.y - a.y) / (b.x - a.x); } return sSlope; } void abcCount(Point a, Point b) {//计算直线一般式ABC if (b.y-a.y==0) { this.A = 0; this.B = 1; this.C = -b.y; } else if (a.x - b.x==0){ this.A = 1; this.B = 0; this.C = -a.x; } else { this.A = b.y - a.y; this.B = a.x - b.x; this.C = b.x * a.y - b.y * a.x; } } boolean parallel(Line x1, Line x2) {//平行线判断 double slope1, slope2; slope1 = x1.slope(x1.zmy[0], x1.zmy[1]); slope2 = x1.slope(x2.zmy[0], x2.zmy[1]); if (slope1 == slope2)//斜率相等 return true; else return false; } double lengthCount(Point a) {//求点a到此直线的距离 double length; length = Math.abs(this.A * a.x + this.B * a.y + this.C) / Math.sqrt(Math.pow(this.A, 2) + Math.pow(this.B, 2)); return length; } } class Triangle{ Point A, B, C; Line x1, x2, x3; public Triangle(){ } public Triangle(Point p1,Point p2,Point p3){ A = p1; B = p2; C = p3; } boolean triangleJudge(Point A, Point B, Point C) {//判断三角形是否合法 int judge = 1; Line x1 = new Line(); x1.A = B.y - A.y; x1.B = A.x - B.x; x1.C = B.x * A.y - B.y * A.x; if (x1.A * C.x + x1.B * C.y + x1.C == 0)//三点共线时不能构成三角形 judge = 0; if (judge == 1)//如果是合法三角形 return true; else return false; } public void abcCount(){ x1.abcCount(A,B); x2.abcCount(A,C); x3.abcCount(B,C); } public void areaCount(Triangle tria , Line x){ if (((x.A*tria.A.x+ x.B*tria.A.y+ x.C==0)&&(x.A*tria.B.x+ x.B*tria.B.y+ x.C==0))||((x.A*tria.C.x+ x.B*tria.C.y+ x.C==0)&&(x.A*tria.B.x+ x.B*tria.B.y+ x.C==0))||((x.A*tria.A.x+ x.B*tria.A.y+ x.C==0)&&(x.A*tria.C.x+ x.B*tria.C.y+ x.C==0))){ //如果顶点带入直线x方程成立,说明直线和边重合 System.out.print("The line is coincide with one of the lines"); } else {//当x和三条边都没有交点时 if (!四边形.pointOnLine(四边形.getDian(x,x1),x1)&&(!四边形.pointOnLine(四边形.getDian(x,x2),x2))&&(!四边形.pointOnLine(四边形.getDian(x,x3),x3))&&tria.A.x*x.A+tria.A.y*x.B+x.C!=0&&tria.B.x*x.A+tria.B.y*x.B+x.C!=0&&tria.C.x*x.A+tria.C.y*x.B+x.C!=0){ System.out.print("0"); }//当只有一个交点时 else if ((x.A * tria.A.x + x.B * tria.A.y + x.C==0&&!四边形.pointOnLine(四边形.getDian(x,x3),x3))||(x.A * tria.B.x + x.B * tria.B.y + x.C==0&&!四边形.pointOnLine(四边形.getDian(x,x2),x2))|| (x.A * tria.C.x + x.B * tria.C.y + x.C==0&&!四边形.pointOnLine(四边形.getDian(x,x1),x1))){ System.out.print("1"); } else {//当有两个交点时 double tArea = Math.sqrt(Math.pow(tria.A.x-tria.B.x,2)+Math.pow(tria.A.y-tria.B.y,2))*tria.x1.lengthCount(tria.C)/2; double area1,area2; double l1,l2,l3; Point dian1 = new Point(); Point dian2 = new Point(); Point dian3 = new Point(); int jJudge = 1; if (x.A * tria.A.x + x.B * tria.A.y + x.C==0){//过A点将三角形分成两个三角形 dian1 = tria.A;//交点1为A点 dian2 = 四边形.getDian(x, tria.x3);//计算交点2 l1 = Math.sqrt(Math.pow(dian1.x-dian2.x,2)+Math.pow(dian1.y-dian2.y,2));//计算底边长度 l2 = x.lengthCount(tria.B);//计算B到直线x的距离 l3 = x.lengthCount(tria.C);//计算C到直线x的距离 area1 = l1*l2/2; area2 = l1*l3/2; jJudge = 0; if (area2>area1){ System.out.print("2 "+四边形.change(area1)+" "+四边形.change(area2)); } else System.out.print("2 "+四边形.change(area2)+" "+四边形.change(area1)); } if (x.A * tria.B.x + x.B * tria.B.y + x.C==0){//过B点将三角形分成两个三角形 dian1 = tria.B; dian2 = 四边形.getDian(x, tria.x2); l1 = Math.sqrt(Math.pow(dian1.x-dian2.x,2)+Math.pow(dian1.y-dian2.y,2)); l2 = x.lengthCount(tria.C); l3 = x.lengthCount(tria.A); area1 = l1*l2/2; area2 = l1*l3/2; jJudge = 0; if (area2>area1){ System.out.print("2 "+四边形.change(area1)+" "+四边形.change(area2)); } else System.out.print("2 "+四边形.change(area2)+" "+四边形.change(area1)); } if (x.A * tria.C.x + x.B * tria.C.y + x.C==0){////过C点将三角形分成两个三角形 dian1 = tria.C; dian2 = 四边形.getDian(x, tria.x1); l1 = Math.sqrt(Math.pow(dian1.x-dian2.x,2)+Math.pow(dian1.y-dian2.y,2)); l2 = x.lengthCount(tria.B); l3 = x.lengthCount(tria.A); area1 = l1*l2/2; area2 = l1*l3/2; jJudge = 0; if (area2>area1){ System.out.print("2 "+四边形.change(area1)+" "+四边形.change(area2)); } else System.out.print("2 "+四边形.change(area2)+" "+四边形.change(area1)); } //当直线x和某条边的交点不在三角形上时,则两个交点和该边相对顶点会构成一个三角形(如直线和边AB的交点不在三角形上,则与边AC、BC相交与点E、F,此时CEF是一个三角形) // 此时则可通过计算该边相对顶点到直线的距离计算出其中一个划分后面积,再拿总面积减去该部分得到剩下的面积,下面的代码就是依此编写的 if (!四边形.pointOnLine(四边形.getDian(x,x1),x1)&&jJudge!=0){//直线与x1的交点不在三角形的边上 dian1 = 四边形.getDian(x, tria.x2); dian2 = 四边形.getDian(x, tria.x3); l1 = Math.sqrt(Math.pow(dian1.x-dian2.x,2)+Math.pow(dian1.y-dian2.y,2));//计算两个交点的距离 l2 = x.lengthCount(tria.C);//计算顶点C到直线的距离 area1 = l2*l1/2; area2 = tArea - area1; if (area2>area1){ System.out.print("2 "+四边形.change(area1)+" "+四边形.change(area2)); } else System.out.print("2 "+四边形.change(area2)+" "+四边形.change(area1)); } if (!四边形.pointOnLine(四边形.getDian(x,x2),x2)&&jJudge!=0){ dian1 = 四边形.getDian(x, tria.x1); dian2 = 四边形.getDian(x, tria.x3); l1 = Math.sqrt(Math.pow(dian1.x-dian2.x,2)+Math.pow(dian1.y-dian2.y,2)); l2 = x.lengthCount(tria.B); area1 = l2*l1/2; area2 = tArea - area1; if (area2>area1){ System.out.print("2 "+四边形.change(area1)+" "+四边形.change(area2)); } else System.out.print("2 "+四边形.change(area2)+" "+四边形.change(area1)); } if (!四边形.pointOnLine(四边形.getDian(x,x3),x3)&&jJudge!=0){ dian1 = 四边形.getDian(x, tria.x2); dian2 = 四边形.getDian(x, tria.x1); l1 = Math.sqrt(Math.pow(dian1.x-dian2.x,2)+Math.pow(dian1.y-dian2.y,2)); l2 = x.lengthCount(tria.A); area1 = l2*l1/2; area2 = tArea - area1; if (area2>area1){ System.out.print("2 "+四边形.change(area1)+" "+四边形.change(area2)); } else System.out.print("2 "+四边形.change(area2)+" "+四边形.change(area1)); } } } } } class Quadrilateral{ Point A, B, C, D; Line AB, BC, CD, DA, AC, BD; public void setA(Point a) { A = a; } public void setB(Point b) { B = b; } public void setC(Point c) { C = c; } public void setD(Point d) { D = d; } public void abcSet() { AB.abcCount(A, B); BC.abcCount(B, C); CD.abcCount(C, D); DA.abcCount(D, A); AC.abcCount(A, C); BD.abcCount(B, D); } boolean quadrilateralJudgeDemo(Point A, Point B, Point C) {//判断三点是否共线 int judge = 1; Line x1 = new Line(); x1.A = B.y - A.y; x1.B = A.x - B.x; x1.C = B.x * A.y - B.y * A.x; if (x1.A * C.x + x1.B * C.y + x1.C == 0)//三点共线时 judge = 0; if (judge == 1)//如果不存在三点共线 return true; else return false;//三点共线 } boolean quadrilateralJudge() {//判断四边形是否合法 if (!quadrilateralJudgeDemo(A, B, C) || !quadrilateralJudgeDemo(B, C, D) || !quadrilateralJudgeDemo(A, C, D)|| !quadrilateralJudgeDemo(A,B,D)) { return false; } 四边形.lineSet(this); this.abcSet(); if (!AB.parallel(AB, CD)) { Point p = new Point(); p = 四边形.getDian(AB, CD); if (((p.x > Math.min(A.x, B.x) && p.x < Math.max(A.x, B.x)) || (p.y > Math.min(A.y,B.y) && p.y < Math.max(A.y, B.y)))&& ((p.x > Math.min(C.x, D.x) && p.x < Math.max(C.x, D.x)) || (p.y > Math.min(C.y, D.y) && p.y < Math.max(C.y, D.y)))) { return false; } } if (!DA.parallel(DA,BC)) { Point p = new Point(); p = 四边形.getDian(DA, BC); if (((p.x > Math.min(A.x, D.x) && p.x < Math.max(A.x, D.x)) || (p.y > Math.min(A.y, D.y) && p.y < Math.max(A.y, D.y))) && ((p.x > Math.min(C.x, B.x) && p.x < Math.max(C.x, B.x)) || (p.y > Math.min(C.y, B.y) && p.y < Math.max(C.y,B.y)))) { return false; } } return true; } boolean parallelogram() {//平行四边形的判断 if (AB.parallel(AB, CD) && BC.parallel(BC, DA) && A.count(B) == C.count(D) && D.count(A) == B.count(C)) { return true; } else { return false; } } boolean Diamond() {//菱形判断 if (A.count(B) == B.count(C)) return true; else return false; } boolean rectangle() {//矩形判断 if ((AB.slope(A,B)==1000000000&&BC.slope(B,C)==0)||(AB.slope(A,B)==0&&BC.slope(B,C)==1000000000)||AB.slope(A,B)*BC.slope(B,C)==-1) return true; else return false; } }
类图及复杂度:
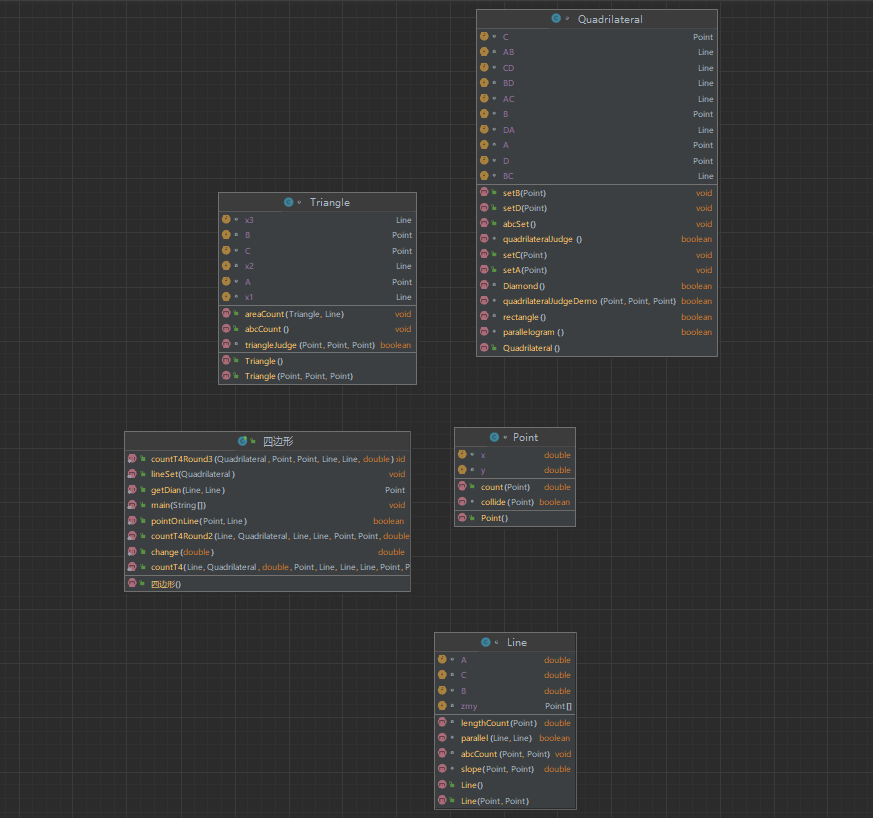
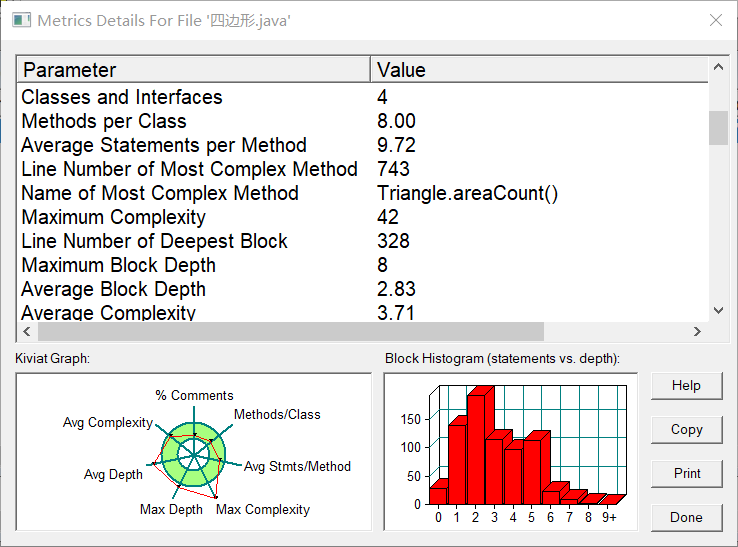
还行,有四个在合适范围内,我的评价是非常满意(bushi),可以看到深度和复杂度方面还有很多可改进的地方。
2. 点线形系列5-凸五边形的计算-1
题目要求:
用户输入一组选项和数据,进行与五边形有关的计算。
以下五边形顶点的坐标要求按顺序依次输入,连续输入的两个顶点是相邻顶点,第一个和最后一个输入的顶点相邻。
选项包括:
1:输入五个点坐标,判断是否是五边形,判断结果输出true/false。
2:输入五个点坐标,判断是凹五边形(false)还是凸五边形(true),如果是凸五边形,则再输出五边形周长、面积,结果之间以一个英文空格符分隔。 若五个点坐标无法构成五边形,输出"not a pentagon"
3:输入七个点坐标,前两个点构成一条直线,后五个点构成一个凸五边形、凸四边形或凸三角形,输出直线与五边形、四边形或三角形相交的交点数量。如果交点有两个,再按面积从小到大输出被直线分割成两部分的面积(不换行)。若直线与多边形形的一条边线重合,输出"The line is coincide with one of the lines"。若后五个点不符合五边形输入,若前两点重合,输出"points coincide"。
以上3选项中,若输入的点无法构成多边形,则输出"not a polygon"。输入的五个点坐标可能存在冗余,假设多边形一条边上两个端点分别是x、y,边线中间有一点z,另一顶点s:
1)符合要求的输入:顶点重复或者z与xy都相邻,如:x x y s、x z y s、x y x s、s x y y。此时去除冗余点,保留一个x、一个y。
2) 不符合要求的输入:z不与xy都相邻,如:z x y s、x z s y、x s z y
题目分析:
与上一题相同的地方就不做额外分析了,解题思路和上一题还是非常类似的,包括这三小题也只是五边形中更为简单的前三小题,难度不大。这一题主要还有以下问题:
1.五边形构成是否合法
通过得到的点坐标对五边形构成情况及五边形凹凸性进行一个判断,反馈到程序中
2.特殊的四边形和三角形构成情况
首先是点重合情况,排除重合后看剩余点的数量和其构成的形状是否合法。另一种情况就是1/2例三点共线,分别得到四边/三角形,同样的,在对照三点的位置和输入顺序后得出相应结论。
代码及其注释:
package 博客2B; import java.math.BigDecimal; import java.util.Scanner; public class 五边形 { public static void main(String[] args) { Scanner sc = new Scanner(System.in); Point[] points = new Point[7]; int judge = 1, judge2 = 1;//初始化错误输入判断数 String zz = "^[+-]?(0|(0\\.\\d+)?|[1-9]\\d*(\\.\\d+)?)$";//正则表达式 String input = sc.nextLine();//接收输入 if ((input.charAt(0) != '1' && input.charAt(0) != '2' && input.charAt(0) != '3' )|| input.charAt(1) != ':') judge = 0;//当开头不满足“(1~3):”格式时,给判断数置0 String text = input.substring(2);//去除开头 String[] zmy = text.split(" ");//按照空格分割字符串 for (int z = 0; z < zmy.length; z++) { String[] zsh = zmy[z].split(",");//按照,分割字符串 if (zsh.length != 2) {//当坐标格式不为x,x时即有多余成分(such as: ,,)判断数置0 judge2 = 0; break; } if (!zsh[0].matches(zz) || !zsh[1].matches(zz)) {//当子字符串格式不匹配时,判断数置0 judge2 = 0; break; } Point a = new Point(); points[z] = a; points[z].x = Double.parseDouble(zsh[0]); points[z].y = Double.parseDouble(zsh[1]); } if (judge == 0) {//错误输入1 System.out.print("Wrong Format"); } else if (judge2 == 0) {//错误输入二 System.out.print("Wrong Format"); } else if ((input.charAt(0) == '1' || input.charAt(0) == '2') && zmy.length != 5 || (input.charAt(0) == '3' && zmy.length != 7) ) { //选项和输入的点的个数不匹配时 System.out.print("wrong number of points"); } else { if (input.charAt(0)=='1'){ Pentagon pen = new Pentagon(points[0],points[1],points[2],points[3],points[4]); pen.lineSet(); System.out.print(pen.judge()); } else if (input.charAt(0)=='2'){//2:0,0 1,0 2,1 1,2 0,2 String outS; double length,area; Pentagon pen = new Pentagon(points[0],points[1],points[2],points[3],points[4]); pen.lineSet(); if (!pen.judge())//2:0,0 10,0 5,-5 10,-10 0,-10 System.out.print("not a pentagon"); else { if (((!pointOnLineInclude(getDian(pen.AB,pen.CD),pen.AB)&&!pointOnLineInclude(getDian(pen.AB,pen.CD),pen.CD))||pen.AB.parallel(pen.AB,pen.CD))&& ((!pointOnLineInclude(getDian(pen.AB,pen.DE),pen.AB)&&!pointOnLineInclude(getDian(pen.AB,pen.DE),pen.DE))||pen.AB.parallel(pen.AB,pen.DE))&& ((!pointOnLineInclude(getDian(pen.BC,pen.DE),pen.BC)&&!pointOnLineInclude(getDian(pen.BC,pen.DE),pen.DE))||pen.BC.parallel(pen.BC,pen.DE))&& ((!pointOnLineInclude(getDian(pen.BC,pen.EA),pen.BC)&&!pointOnLineInclude(getDian(pen.BC,pen.EA),pen.EA))||pen.BC.parallel(pen.BC,pen.EA))&& ((!pointOnLineInclude(getDian(pen.EA,pen.CD),pen.CD)&&!pointOnLineInclude(getDian(pen.EA,pen.CD),pen.EA))||pen.EA.parallel(pen.EA,pen.CD))){ outS = "true"; length = pen.A.count(pen.B) + pen.B.count(pen.C) + pen.C.count(pen.D) + pen.D.count(pen.E) + pen.E.count(pen.A); area = 0.5*(pen.BC.lengthCount(pen.A)*pen.B.count(pen.C)+pen.CD.lengthCount(pen.A)*pen.D.count(pen.C)+pen.DE.lengthCount(pen.A)*pen.D.count(pen.E)); System.out.print(outS+" "+change(length)+" "+change(area)); } else { System.out.print("false"); } } } else { if (points[0].collide(points[1])) System.out.print("points coincide"); else { int mark; int sign; int y = 0; Line x = new Line(points[0], points[1]); x.abcCount(points[0],points[1]); Point [] pointsUnRe = new Point[5]; for (int z = 2 ; z < points.length ; z++){//去除重复点 sign = 1 ; if (z==2) {//第一个点无脑放 pointsUnRe[y] = points[z]; y++; } else{ for (int m = 0 ; m < y; m++){//接下来的每一个都和无重复点数组里已有的进行比较 if (points[z].collide(pointsUnRe[m]))//如果重复,则弃置 sign = 0; } if (sign == 1){ pointsUnRe[y] = points[z];//反之也放入无重复点数组 y++; } } } int length = y;//可用点数组的实际长度 if (length<3||length>5) System.out.print("not a polygon"); else if (length==3){//3:0,0 2,2 0,0 0,4 4,0 0,4 4,0 Triangle tri = new Triangle(pointsUnRe[0],pointsUnRe[1],pointsUnRe[2]); tri.lineSet(); if (!tri.triangleJudge(tri.A,tri.B,tri.C)) System.out.print("not a polygon"); else tri.areaCount(tri,x); } else if (length==4){//3:0,10 10,0 0,0 10,0 10,10 0,10 10,0 Quadrilateral qua = new Quadrilateral(pointsUnRe[0],pointsUnRe[1],pointsUnRe[2],pointsUnRe[3]); qua.lineSet(); if (!qua.quadrilateralJudge()) System.out.print("not a polygon"); else qua.areaCount(qua,x); } else {//3:10,0 120,0 0,0 6,0 7,0 8,0 8,6 int tMark = 0; int qMark = 0; int pMark = 0; int oMark = 0; Triangle tri = new Triangle(); Quadrilateral qua = new Quadrilateral(); Pentagon pen = new Pentagon(pointsUnRe[0],pointsUnRe[1],pointsUnRe[2],pointsUnRe[3],pointsUnRe[4]); pen.lineSet(); Line AC = new Line(pen.A,pen.C); AC.abcCount(pen.A,pen.C); Line BD = new Line(pen.B,pen.D); BD.abcCount(pen.B,pen.D); Line CE = new Line(pen.C,pen.E); CE.abcCount(pen.C,pen.E); Line DA = new Line(pen.D,pen.A); DA.abcCount(pen.D,pen.A); Line EB = new Line(pen.E,pen.B); EB.abcCount(pen.E,pen.B); if (pen.B.x* AC.A+pen.B.y* AC.B+ AC.C==0&&pointOnLine(pen.B,AC)&&pen.D.x* CE.A+pen.D.y* CE.B+CE.C==0&&pointOnLine(pen.D,CE)){ Triangle triangle = new Triangle(pen.A,pen.C,pen.E);//A B C||D E A tri = triangle; tMark = 1; } else if (pen.C.x* BD.A+pen.C.y* BD.B+ BD.C==0&&pointOnLine(pen.C,BD)&&pen.A.x* EB.A+pen.A.y* EB.B+EB.C==0&&pointOnLine(pen.A,EB)){ Triangle triangle = new Triangle(pen.B,pen.D,pen.E);//B C D||E A B tri = triangle; tMark = 1; } else if (pen.C.x* BD.A+pen.C.y* BD.B+ BD.C==0&&pointOnLine(pen.C,BD)&&pen.E.x* DA.A+pen.E.y* DA.B+DA.C==0&&pointOnLine(pen.E,DA)){ Triangle triangle = new Triangle(pen.A,pen.B,pen.D);//B C D||D E A tri = triangle; tMark = 1; } else if (pen.B.x* AC.A+pen.B.y* AC.B+ AC.C==0&&pointOnLine(pen.B,AC)&&pen.E.x* DA.A+pen.E.y* DA.B+DA.C==0&&pointOnLine(pen.E,DA)){ Triangle triangle = new Triangle(pen.A,pen.C,pen.D);//A B C||D E A tri = triangle; tMark = 1; } else if (pen.D.x* CE.A+pen.D.y* CE.B+ CE.C==0&&pointOnLine(pen.D,CE)&&pen.A.x* EB.A+pen.A.y* EB.B+EB.C==0&&pointOnLine(pen.A,EB)){ Triangle triangle = new Triangle(pen.B,pen.C,pen.E);//C D E||E A B tri = triangle; tMark = 1; } else if (pen.A.x*EB.A+pen.A.y*EB.B+ EB.C==0&&pointOnLine(pen.A,EB)){ Quadrilateral quadrilateral = new Quadrilateral(pen.B,pen.C,pen.D,pen.E); qua = quadrilateral; qMark = 1; } else if (pen.B.x*AC.A+pen.B.y*AC.B+ AC.C==0&&pointOnLine(pen.B,AC)){ Quadrilateral quadrilateral = new Quadrilateral(pen.A,pen.C,pen.D,pen.E); qua = quadrilateral; qMark = 1; } else if (pen.C.x*BD.A+pen.C.y*BD.B+ BD.C==0&&pointOnLine(pen.C,BD)){ Quadrilateral quadrilateral = new Quadrilateral(pen.A,pen.B,pen.D,pen.E); qua = quadrilateral; qMark = 1; } else if (pen.D.x*CE.A+pen.D.y*CE.B+ CE.C==0&&pointOnLine(pen.D,CE)){ Quadrilateral quadrilateral = new Quadrilateral(pen.A,pen.B,pen.C,pen.E); qua = quadrilateral; qMark = 1; } else if (pen.E.x*DA.A+pen.E.y*DA.B+ DA.C==0&&pointOnLine(pen.E,DA)){ Quadrilateral quadrilateral = new Quadrilateral(pen.A,pen.B,pen.C,pen.D); qua = quadrilateral; qMark = 1; } else if (pen.judge()) pMark = 1; else { oMark = 1; System.out.print("not a polygon"); } if (oMark==0) { if (tMark == 1 && qMark == 0 && pMark == 0) { tri.lineSet(); tri.areaCount(tri, x); } else if (tMark == 0 && qMark == 1 && pMark == 0) { qua.lineSet(); qua.areaCount(qua, x); } else if (tMark==0&&qMark==0&&pMark==1){ pen.areaCount(x); } else System.out.print("not a polygon"); } } } } } } public static boolean pointOnLine(Point p,Line l ){//不含端点 if (l.A==0){ if (p.x>Math.min(l.zmy[0].x,l.zmy[1].x)&&p.x<Math.max(l.zmy[0].x,l.zmy[1].x)) return true; else return false; } else if (l.B==0){ if (p.y>Math.min(l.zmy[0].y,l.zmy[1].y)&&p.y<Math.max(l.zmy[0].y,l.zmy[1].y)) return true; else return false; } else { if ((p.x > Math.min(l.zmy[0].x, l.zmy[1].x) && p.x < Math.max(l.zmy[0].x, l.zmy[1].x)) && (p.y > Math.min(l.zmy[0].y, l.zmy[1].y) && p.y < Math.max(l.zmy[0].y, l.zmy[1].y))) return true;//点在线段上 else return false; } } public static boolean pointOnLineInclude(Point p,Line l ){//含端点 if (l.A==0){ if (p.x>=Math.min(l.zmy[0].x,l.zmy[1].x)&&p.x<=Math.max(l.zmy[0].x,l.zmy[1].x)) return true; else return false; } else if (l.B==0){ if (p.y>=Math.min(l.zmy[0].y,l.zmy[1].y)&&p.y<=Math.max(l.zmy[0].y,l.zmy[1].y)) return true; else return false; } else { if ((p.x >= Math.min(l.zmy[0].x, l.zmy[1].x) && p.x <= Math.max(l.zmy[0].x, l.zmy[1].x)) && (p.y >= Math.min(l.zmy[0].y, l.zmy[1].y) && p.y <= Math.max(l.zmy[0].y, l.zmy[1].y))) return true;//点在线段上 else return false; } } public static Point getDian(Line x, Line y) {//计算交点 Point re = new Point(); re.x = (y.C * x.B - x.C * y.B) / (x.A * y.B - y.A * x.B); re.y = (x.C * y.A - y.C * x.A) / (x.A * y.B - y.A * x.B); return re; } public static double change(double d) {//转化为三位小数 double d1; BigDecimal big = new BigDecimal(d); d1 = big.setScale(3, BigDecimal.ROUND_HALF_UP).doubleValue(); return d1; } } class Point { double x, y; public Point() { } public double count(Point a) {//求两点之间距离 double fin; fin = Math.sqrt(Math.pow((a.x - this.x), 2) + Math.pow((a.y - this.y), 2)); return fin; } boolean collide(Point b) {//求重合点 if (this.x == b.x && this.y == b.y) return true; else return false; } boolean collidePlus(Point a, Point b){ if (this.collide(a)&&this.collide(b)) return true; else return false; } public boolean pointsOneLine(Point p1 , Point p2){ Line l = new Line(p1,p2); l.abcCount(p1,p2); if (x* l.A+y* l.B+ l.C==0) return true; else return false; } } class Line { Point[] zmy = new Point[2]; double A, B, C; public Line() { } public Line(Point a, Point b) { zmy[0] = a; zmy[1] = b; } double slope(Point a, Point b) {//求斜率 double sSlope; if (b.x == a.x) sSlope = 1000000000; else { sSlope = (b.y - a.y) / (b.x - a.x); } return sSlope; } void abcCount(Point a, Point b) {//计算直线一般式ABC if (b.y-a.y==0) { this.A = 0; this.B = 1; this.C = -b.y; } else if (a.x - b.x==0){ this.A = 1; this.B = 0; this.C = -a.x; } else { this.A = b.y - a.y; this.B = a.x - b.x; this.C = b.x * a.y - b.y * a.x; } } boolean parallel(Line x1, Line x2) {//平行线判断 double slope1, slope2; slope1 = x1.slope(x1.zmy[0], x1.zmy[1]); slope2 = x1.slope(x2.zmy[0], x2.zmy[1]); if (slope1 == slope2)//斜率相等 return true; else return false; } double lengthCount(Point a) {//求点a到此直线的距离 double length; length = Math.abs(this.A * a.x + this.B * a.y + this.C) / Math.sqrt(Math.pow(this.A, 2) + Math.pow(this.B, 2)); return length; } } class Triangle{ Point A, B, C; Line x1, x2, x3; public Triangle(){ } public Triangle(Point p1,Point p2,Point p3){ A = p1; B = p2; C = p3; } boolean triangleJudge(Point A, Point B, Point C) {//判断三角形是否合法 int judge = 1; Line x1 = new Line(); x1.A = B.y - A.y; x1.B = A.x - B.x; x1.C = B.x * A.y - B.y * A.x; if (x1.A * C.x + x1.B * C.y + x1.C == 0)//三点共线时不能构成三角形 judge = 0; if (judge == 1)//如果是合法三角形 return true; else return false; } public void lineSet(){ x1 = new Line(A,B); x2 = new Line(A,C); x3 = new Line(B,C); x1.abcCount(A,B); x2.abcCount(A,C); x3.abcCount(B,C); } public void areaCount(Triangle tria , Line x){//3:0,0 2,2 0,0 0,4 4,0 0,4 4,0 if (((x.A*tria.A.x+ x.B*tria.A.y+ x.C==0)&&(x.A*tria.B.x+ x.B*tria.B.y+ x.C==0))||((x.A*tria.C.x+ x.B*tria.C.y+ x.C==0)&&(x.A*tria.B.x+ x.B*tria.B.y+ x.C==0))||((x.A*tria.A.x+ x.B*tria.A.y+ x.C==0)&&(x.A*tria.C.x+ x.B*tria.C.y+ x.C==0))){ //如果顶点带入直线x方程成立,说明直线和边重合 System.out.print("The line is coincide with one of the lines"); } else {//当x和三条边都没有交点时 if (!五边形.pointOnLine(五边形.getDian(x,x1),x1)&&(!五边形.pointOnLine(五边形.getDian(x,x2),x2))&&(!五边形.pointOnLine(五边形.getDian(x,x3),x3))&&tria.A.x*x.A+tria.A.y*x.B+x.C!=0&&tria.B.x*x.A+tria.B.y*x.B+x.C!=0&&tria.C.x*x.A+tria.C.y*x.B+x.C!=0){ System.out.print("0"); }//当只有一个交点时 else if ((x.A * tria.A.x + x.B * tria.A.y + x.C==0&&!五边形.pointOnLine(五边形.getDian(x,x3),x3))||(x.A * tria.B.x + x.B * tria.B.y + x.C==0&&!五边形.pointOnLine(五边形.getDian(x,x2),x2))|| (x.A * tria.C.x + x.B * tria.C.y + x.C==0&&!五边形.pointOnLine(五边形.getDian(x,x1),x1))){ System.out.print("1"); } else {//当有两个交点时 double tArea = Math.sqrt(Math.pow(tria.A.x-tria.B.x,2)+Math.pow(tria.A.y-tria.B.y,2))*tria.x1.lengthCount(tria.C)/2; double area1,area2; double l1,l2,l3; Point dian1 = new Point(); Point dian2 = new Point(); Point dian3 = new Point(); int jJudge = 1; if (x.A * tria.A.x + x.B * tria.A.y + x.C==0){//过A点将三角形分成两个三角形 dian1 = tria.A;//交点1为A点 dian2 = 五边形.getDian(x, tria.x3);//计算交点2 l1 = Math.sqrt(Math.pow(dian1.x-dian2.x,2)+Math.pow(dian1.y-dian2.y,2));//计算底边长度 l2 = x.lengthCount(tria.B);//计算B到直线x的距离 l3 = x.lengthCount(tria.C);//计算C到直线x的距离 area1 = l1*l2/2; area2 = l1*l3/2; jJudge = 0; if (area2>area1){ System.out.print("2 "+ 五边形.change(area1)+" "+ 五边形.change(area2)); } else System.out.print("2 "+ 五边形.change(area2)+" "+ 五边形.change(area1)); } if (x.A * tria.B.x + x.B * tria.B.y + x.C==0){//过B点将三角形分成两个三角形 dian1 = tria.B; dian2 = 五边形.getDian(x, tria.x2); l1 = Math.sqrt(Math.pow(dian1.x-dian2.x,2)+Math.pow(dian1.y-dian2.y,2)); l2 = x.lengthCount(tria.C); l3 = x.lengthCount(tria.A); area1 = l1*l2/2; area2 = l1*l3/2; jJudge = 0; if (area2>area1){ System.out.print("2 "+ 五边形.change(area1)+" "+ 五边形.change(area2)); } else System.out.print("2 "+ 五边形.change(area2)+" "+ 五边形.change(area1)); } if (x.A * tria.C.x + x.B * tria.C.y + x.C==0){////过C点将三角形分成两个三角形 dian1 = tria.C; dian2 = 五边形.getDian(x, tria.x1); l1 = Math.sqrt(Math.pow(dian1.x-dian2.x,2)+Math.pow(dian1.y-dian2.y,2)); l2 = x.lengthCount(tria.B); l3 = x.lengthCount(tria.A); area1 = l1*l2/2; area2 = l1*l3/2; jJudge = 0; if (area2>area1){ System.out.print("2 "+ 五边形.change(area1)+" "+ 五边形.change(area2)); } else System.out.print("2 "+ 五边形.change(area2)+" "+ 五边形.change(area1)); } //当直线x和某条边的交点不在三角形上时,则两个交点和该边相对顶点会构成一个三角形(如直线和边AB的交点不在三角形上,则与边AC、BC相交与点E、F,此时CEF是一个三角形) // 此时则可通过计算该边相对顶点到直线的距离计算出其中一个划分后面积,再拿总面积减去该部分得到剩下的面积,下面的代码就是依此编写的 if (!五边形.pointOnLine(五边形.getDian(x,x1),x1)&&jJudge!=0){//直线与x1的交点不在三角形的边上 dian1 = 五边形.getDian(x, tria.x2); dian2 = 五边形.getDian(x, tria.x3); l1 = Math.sqrt(Math.pow(dian1.x-dian2.x,2)+Math.pow(dian1.y-dian2.y,2));//计算两个交点的距离 l2 = x.lengthCount(tria.C);//计算顶点C到直线的距离 area1 = l2*l1/2; area2 = tArea - area1; if (area2>area1){ System.out.print("2 "+ 五边形.change(area1)+" "+ 五边形.change(area2)); } else System.out.print("2 "+ 五边形.change(area2)+" "+ 五边形.change(area1)); } if (!五边形.pointOnLine(五边形.getDian(x,x2),x2)&&jJudge!=0){ dian1 = 五边形.getDian(x, tria.x1); dian2 = 五边形.getDian(x, tria.x3); l1 = Math.sqrt(Math.pow(dian1.x-dian2.x,2)+Math.pow(dian1.y-dian2.y,2)); l2 = x.lengthCount(tria.B); area1 = l2*l1/2; area2 = tArea - area1; if (area2>area1){ System.out.print("2 "+ 五边形.change(area1)+" "+ 五边形.change(area2)); } else System.out.print("2 "+ 五边形.change(area2)+" "+ 五边形.change(area1)); } if (!五边形.pointOnLine(五边形.getDian(x,x3),x3)&&jJudge!=0){ dian1 = 五边形.getDian(x, tria.x2); dian2 = 五边形.getDian(x, tria.x1); l1 = Math.sqrt(Math.pow(dian1.x-dian2.x,2)+Math.pow(dian1.y-dian2.y,2)); l2 = x.lengthCount(tria.A); area1 = l2*l1/2; area2 = tArea - area1; if (area2>area1){ System.out.print("2 "+ 五边形.change(area1)+" "+ 五边形.change(area2)); } else System.out.print("2 "+ 五边形.change(area2)+" "+ 五边形.change(area1)); } } } } } class Quadrilateral{ Point A, B, C, D; Line AB, BC, CD, DA, AC, BD; public Quadrilateral(){ } public Quadrilateral(Point A,Point B,Point C, Point D){ this.A = A; this.B = B; this.C = C; this.D = D; } public void lineSet() {//初始化四边形各边 AB = new Line(A, B); BC = new Line(B, C); CD = new Line(C, D); DA = new Line(D, A); AC = new Line(A, C); BD = new Line(B, D); AB.abcCount(A,B); BC.abcCount(B,C); CD.abcCount(C,D); DA.abcCount(D,A); AC.abcCount(A,C); BD.abcCount(B,D); } boolean quadrilateralJudge() {//判断四边形是否合法 if (A.pointsOneLine(B,C) || B.pointsOneLine(C,D) || A.pointsOneLine(C,D)|| A.pointsOneLine(B,D)) { return false; } lineSet(); if (!AB.parallel(AB, CD)) { Point p = new Point(); p = 五边形.getDian(AB, CD); if (((p.x > Math.min(A.x, B.x) && p.x < Math.max(A.x, B.x)) || (p.y > Math.min(A.y,B.y) && p.y < Math.max(A.y, B.y)))&& ((p.x > Math.min(C.x, D.x) && p.x < Math.max(C.x, D.x)) || (p.y > Math.min(C.y, D.y) && p.y < Math.max(C.y, D.y)))) { return false; } } if (!DA.parallel(DA,BC)) { Point p = new Point(); p = 五边形.getDian(DA, BC); if (((p.x > Math.min(A.x, D.x) && p.x < Math.max(A.x, D.x)) || (p.y > Math.min(A.y, D.y) && p.y < Math.max(A.y, D.y))) && ((p.x > Math.min(C.x, B.x) && p.x < Math.max(C.x, B.x)) || (p.y > Math.min(C.y, B.y) && p.y < Math.max(C.y,B.y)))) { return false; } } return true; } public void areaCount(Quadrilateral qua,Line x){ if ((x.A*qua.A.x+x.B*qua.A.y+x.C==0&&x.A*qua.B.x+x.B*qua.B.y+x.C==0)||(x.A*qua.C.x+x.B*qua.C.y+x.C==0&&x.A*qua.B.x+x.B*qua.B.y+x.C==0)|| (x.A*qua.C.x+x.B*qua.C.y+x.C==0&&x.A*qua.D.x+x.B*qua.D.y+x.C==0)||(x.A*qua.A.x+x.B*qua.A.y+x.C==0&&x.A*qua.D.x+x.B*qua.D.y+x.C==0)) System.out.print("The line is coincide with one of the lines"); else if ((x.parallel(x,AB)||!五边形.pointOnLineInclude(五边形.getDian(x,AB),AB))&& (x.parallel(x,BC)||!五边形.pointOnLineInclude(五边形.getDian(x,BC),BC))&& (x.parallel(x,CD)||!五边形.pointOnLineInclude(五边形.getDian(x,CD),CD))&& (x.parallel(x,DA)||!五边形.pointOnLineInclude(五边形.getDian(x,DA),DA))) System.out.print("0"); else if ( (x.A*A.x+x.B*A.y+x.C==0&&(x.parallel(x,BC)||!五边形.pointOnLineInclude(五边形.getDian(x,BC),BC))&&(x.parallel(x,CD)||!五边形.pointOnLineInclude(五边形.getDian(x,CD),CD)))|| (x.A*B.x+x.B*B.y+x.C==0&&(x.parallel(x,CD)||!五边形.pointOnLineInclude(五边形.getDian(x,CD),CD))&&(x.parallel(x,DA)||!五边形.pointOnLineInclude(五边形.getDian(x,DA),DA)))|| (x.A*C.x+x.B*C.y+x.C==0&&(x.parallel(x,DA)||!五边形.pointOnLineInclude(五边形.getDian(x,DA),DA))&&(x.parallel(x,AB)||!五边形.pointOnLineInclude(五边形.getDian(x,AB),AB)))|| (x.A*D.x+x.B*D.y+x.C==0&&(x.parallel(x,AB)||!五边形.pointOnLineInclude(五边形.getDian(x,AB),AB))&&(x.parallel(x,BC)||!五边形.pointOnLineInclude(五边形.getDian(x,BC),BC))) ) System.out.print("1"); else {//3:0,10 10,0 0,0 10,0 10,10 0,10 10,0 //过某一端点 Double area = 0.5*(AC.lengthCount(B)*A.count(C)+AC.lengthCount(D)*A.count(C)); if (x.A*A.x+x.B*A.y+x.C==0&& 五边形.pointOnLineInclude(五边形.getDian(x,BC),BC)) count3(B,A, 五边形.getDian(x,BC),x,area); else if (x.A*A.x+x.B*A.y+x.C==0&& 五边形.pointOnLineInclude(五边形.getDian(x,CD),CD)) count3(D,A, 五边形.getDian(x,CD),x,area); else if (x.A*B.x+x.B*B.y+x.C==0&& 五边形.pointOnLineInclude(五边形.getDian(x,CD),CD)) count3(C,B, 五边形.getDian(x,CD),x,area); else if (x.A*B.x+x.B*B.y+x.C==0&& 五边形.pointOnLineInclude(五边形.getDian(x,DA),DA)) count3(A,B, 五边形.getDian(x,DA),x,area); else if (x.A*C.x+x.B*C.y+x.C==0&& 五边形.pointOnLineInclude(五边形.getDian(x,DA),DA)) count3(D,C, 五边形.getDian(x,DA),x,area); else if (x.A*C.x+x.B*C.y+x.C==0&& 五边形.pointOnLineInclude(五边形.getDian(x,AB),AB)) count3(B,C, 五边形.getDian(x,AB),x,area); else if (x.A*D.x+x.B*D.y+x.C==0&& 五边形.pointOnLineInclude(五边形.getDian(x,AB),AB)) count3(A,D, 五边形.getDian(x,AB),x,area); else if (x.A*D.x+x.B*D.y+x.C==0&& 五边形.pointOnLineInclude(五边形.getDian(x,BC),BC)) count3(C,D, 五边形.getDian(x,BC),x,area); //不过顶点 else if (!x.parallel(x,AB)&&!x.parallel(x,BC)&& 五边形.pointOnLine(五边形.getDian(x,AB),AB)&& 五边形.pointOnLine(五边形.getDian(x,BC),BC)) count1(B, 五边形.getDian(x,AB), 五边形.getDian(x,BC),x,area); else if (!x.parallel(x,BC)&&!x.parallel(x,CD)&& 五边形.pointOnLine(五边形.getDian(x,BC),BC)&& 五边形.pointOnLine(五边形.getDian(x,CD),CD)) count1(C, 五边形.getDian(x,CD), 五边形.getDian(x,BC),x,area); else if (!x.parallel(x,DA)&&!x.parallel(x,CD)&& 五边形.pointOnLine(五边形.getDian(x,DA),DA)&& 五边形.pointOnLine(五边形.getDian(x,CD),CD)) count1(D, 五边形.getDian(x,DA), 五边形.getDian(x,CD),x,area); else if (!x.parallel(x,DA)&&!x.parallel(x,AB)&& 五边形.pointOnLine(五边形.getDian(x,DA),DA)&& 五边形.pointOnLine(五边形.getDian(x,AB),AB)) count1(A, 五边形.getDian(x,DA), 五边形.getDian(x,AB),x,area); else if (!x.parallel(x,AB)&&!x.parallel(x,CD)&& 五边形.pointOnLine(五边形.getDian(x,AB),AB)&& 五边形.pointOnLine(五边形.getDian(x,CD),CD)) count2(A,D, 五边形.getDian(x,AB), 五边形.getDian(x,CD),x,area); else count2(B,A, 五边形.getDian(x,BC), 五边形.getDian(x,DA),x,area); } } public void count1(Point p1,Point jp1, Point jp2, Line x, Double area){ Double outArea1,outArea2; outArea1 = 0.5*x.lengthCount(p1) * jp1.count(jp2); outArea2 = area-outArea1; if (outArea1<=outArea2){ System.out.print("2 "+ 五边形.change(outArea1)+" "+ 五边形.change(outArea2)); } else System.out.print("2 "+ 五边形.change(outArea2)+" "+ 五边形.change(outArea1)); } public void count2(Point p1, Point p2,Point jp1, Point jp2, Line x, Double area){ Double outArea1,outArea2; Line l = new Line(p1,jp1); l.abcCount(p1,jp1); outArea1 = 0.5*(l.lengthCount(p2)*p1.count(jp1)+x.lengthCount(p2)*jp1.count(jp2)); outArea2 = area - outArea1; if (outArea1<=outArea2){ System.out.print("2 "+ 五边形.change(outArea1)+" "+ 五边形.change(outArea2)); } else System.out.print("2 "+ 五边形.change(outArea2)+" "+ 五边形.change(outArea1)); } public void count3(Point p, Point jp1, Point jp2, Line x, Double area){ Double outArea1,outArea2; outArea1 = 0.5*x.lengthCount(p)*jp1.count(jp2); outArea2 = area-outArea1; if (outArea1<=outArea2){ System.out.print("2 "+ 五边形.change(outArea1)+" "+ 五边形.change(outArea2)); } else System.out.print("2 "+ 五边形.change(outArea2)+" "+ 五边形.change(outArea1)); } } class Pentagon{ Point A,B,C,D,E; Line AB,BC,CD,DE,EA; public Pentagon(){ } public Pentagon(Point A,Point B,Point C,Point D,Point E){ this.A = A; this.B = B; this.C = C; this.D = D; this.E = E; } public void lineSet(){ AB = new Line(A,B); BC = new Line(B,C); CD = new Line(C,D); DE = new Line(D,E); EA = new Line(E,A); AB.abcCount(A,B); BC.abcCount(B,C); CD.abcCount(C,D); DE.abcCount(D,E); EA.abcCount(E,A); } public boolean judge(){ if (A.collide(B)||A.collide(C)||A.collide(D)||A.collide(E)||B.collide(C)||B.collide(D)||B.collide(E)||C.collide(D)|| C.collide(E)||D.collide(E)){ return false; } else if (AB.parallel(AB,BC)||BC.parallel(BC,CD)||CD.parallel(CD,DE)||DE.parallel(DE,EA)||EA.parallel(EA,AB)){ return false; }//AB CD AB DE BC DE BC AE CD AE else if (((五边形.pointOnLine(五边形.getDian(AB,CD),AB)&& 五边形.pointOnLine(五边形.getDian(AB,CD),CD))&&!AB.parallel(AB,CD))|| ((五边形.pointOnLine(五边形.getDian(AB,DE),AB)&& 五边形.pointOnLine(五边形.getDian(AB,DE),DE))&&!AB.parallel(AB,DE))|| ((五边形.pointOnLine(五边形.getDian(BC,DE),BC)&& 五边形.pointOnLine(五边形.getDian(BC,DE),DE))&&!BC.parallel(BC,DE))|| ((五边形.pointOnLine(五边形.getDian(BC,EA),BC)&& 五边形.pointOnLine(五边形.getDian(BC,EA),EA))&&!BC.parallel(BC,EA))|| ((五边形.pointOnLine(五边形.getDian(EA,CD),CD)&& 五边形.pointOnLine(五边形.getDian(EA,CD),EA))&&!EA.parallel(CD,EA)) ) return false; else return true; } public void areaCount(Line x){ if ((x.A*A.x+x.B*A.y+x.C==0&&x.A*B.x+x.B*B.y+x.C==0)||(x.A*C.x+x.B*C.y+x.C==0&&x.A*B.x+x.B*B.y+x.C==0)|| (x.A*C.x+x.B*C.y+x.C==0&&x.A*D.x+x.B*D.y+x.C==0)||(x.A*D.x+x.B*D.y+x.C==0&&x.A*E.x+x.B*E.y+x.C==0)||(x.A*E.x+x.B*E.y+x.C==0&&x.A*A.x+x.B*A.y+x.C==0)) System.out.print("The line is coincide with one of the lines"); else if ((x.parallel(x,AB)||(!五边形.pointOnLineInclude(五边形.getDian(x,AB),AB)))&&(x.parallel(x,BC)||(!五边形.pointOnLineInclude(五边形.getDian(x,BC),BC)))&& (x.parallel(x,CD)||(!五边形.pointOnLineInclude(五边形.getDian(x,CD),CD)))&& (x.parallel(x,DE)||(!五边形.pointOnLineInclude(五边形.getDian(x,DE),DE)))&& (x.parallel(x,EA)||(!五边形.pointOnLineInclude(五边形.getDian(x,EA),EA)))) System.out.print("0"); else if ( (x.A*A.x+x.B+A.y+x.C==0&&(x.parallel(x,BC)||!五边形.pointOnLineInclude(五边形.getDian(x,BC),BC))&&(x.parallel(x,CD)||!五边形.pointOnLineInclude(五边形.getDian(x,CD),CD))&&(x.parallel(x,DE)||!五边形.pointOnLineInclude(五边形.getDian(x,DE),DE)))|| (x.A*B.x+x.B+B.y+x.C==0&&(x.parallel(x,CD)||!五边形.pointOnLineInclude(五边形.getDian(x,CD),CD))&&(x.parallel(x,DE)||!五边形.pointOnLineInclude(五边形.getDian(x,DE),DE))&&(x.parallel(x,EA)||!五边形.pointOnLineInclude(五边形.getDian(x,EA),EA)))|| (x.A*C.x+x.B+C.y+x.C==0&&(x.parallel(x,DE)||!五边形.pointOnLineInclude(五边形.getDian(x,DE),DE))&&(x.parallel(x,EA)||!五边形.pointOnLineInclude(五边形.getDian(x,EA),EA))&&(x.parallel(x,AB)||!五边形.pointOnLineInclude(五边形.getDian(x,AB),AB)))|| (x.A*D.x+x.B+D.y+x.C==0&&(x.parallel(x,EA)||!五边形.pointOnLineInclude(五边形.getDian(x,EA),EA))&&(x.parallel(x,AB)||!五边形.pointOnLineInclude(五边形.getDian(x,AB),AB))&&(x.parallel(x,BC)||!五边形.pointOnLineInclude(五边形.getDian(x,BC),BC)))|| (x.A*E.x+x.B+E.y+x.C==0&&(x.parallel(x,AB)||!五边形.pointOnLineInclude(五边形.getDian(x,AB),AB))&&(x.parallel(x,BC)||!五边形.pointOnLineInclude(五边形.getDian(x,BC),BC))&&(x.parallel(x,CD)||!五边形.pointOnLineInclude(五边形.getDian(x,CD),CD))) ) System.out.print("1"); else { double area; area = 0.5*(BC.lengthCount(A)*B.count(C)+CD.lengthCount(A)*C.count(D)+DE.lengthCount(A)*D.count(E)); //AB if (x.A*A.x+x.B*A.y+x.C==0&& 五边形.pointOnLineInclude(五边形.getDian(x,BC),BC)) count1(B,A, 五边形.getDian(x,BC),x,area); else if (x.A*A.x+x.B*A.y+x.C==0&& 五边形.pointOnLineInclude(五边形.getDian(x,DE),DE)) count1(E,A, 五边形.getDian(x,DE),x,area); else if (x.A*B.x+x.B*B.y+x.C==0&& 五边形.pointOnLineInclude(五边形.getDian(x,CD),CD)) count1(C,B, 五边形.getDian(x,CD),x,area); else if (x.A*B.x+x.B*B.y+x.C==0&& 五边形.pointOnLineInclude(五边形.getDian(x,EA),EA)) count1(A,B, 五边形.getDian(x,EA),x,area); else if (x.A*C.x+x.B*C.y+x.C==0&& 五边形.pointOnLineInclude(五边形.getDian(x,DE),DE)) count1(D,C, 五边形.getDian(x,DE),x,area); else if (x.A*C.x+x.B*C.y+x.C==0&& 五边形.pointOnLineInclude(五边形.getDian(x,AB),AB)) count1(B,C, 五边形.getDian(x,AB),x,area); else if (x.A*D.x+x.B*D.y+x.C==0&& 五边形.pointOnLineInclude(五边形.getDian(x,EA),EA)) count1(E,D, 五边形.getDian(x,EA),x,area); else if (x.A*D.x+x.B*D.y+x.C==0&& 五边形.pointOnLineInclude(五边形.getDian(x,BC),BC)) count1(C,D, 五边形.getDian(x,BC),x,area); else if (x.A*E.x+x.B*E.y+x.C==0&& 五边形.pointOnLineInclude(五边形.getDian(x,AB),AB)) count1(A,E, 五边形.getDian(x,AB),x,area); else if (x.A*E.x+x.B*E.y+x.C==0&& 五边形.pointOnLineInclude(五边形.getDian(x,CD),CD)) count1(D,E, 五边形.getDian(x,CD),x,area); else if (x.A*A.x+x.B*A.y+x.C==0&& 五边形.pointOnLineInclude(五边形.getDian(x,CD),CD)) count2(B,C,A, 五边形.getDian(x,CD),x,area); else if (x.A*B.x+x.B*B.y+x.C==0&& 五边形.pointOnLineInclude(五边形.getDian(x,DE),DE)) count2(C,D,B, 五边形.getDian(x,DE),x,area); else if (x.A*C.x+x.B*C.y+x.C==0&& 五边形.pointOnLineInclude(五边形.getDian(x,EA),EA)) count2(D,E,C, 五边形.getDian(x,EA),x,area); else if (x.A*D.x+x.B*D.y+x.C==0&& 五边形.pointOnLineInclude(五边形.getDian(x,AB),AB)) count2(E,A,D, 五边形.getDian(x,AB),x,area); else if (x.A*E.x+x.B*E.y+x.C==0&& 五边形.pointOnLineInclude(五边形.getDian(x,BC),BC)) count2(A,B,E, 五边形.getDian(x,BC),x,area); else if (五边形.pointOnLine(五边形.getDian(x,AB),AB)&& 五边形.pointOnLine(五边形.getDian(x,BC),BC)) count1(B, 五边形.getDian(x,AB), 五边形.getDian(x,BC),x,area); else if (五边形.pointOnLine(五边形.getDian(x,AB),AB)&& 五边形.pointOnLine(五边形.getDian(x,CD),CD)) { count2(B, C, 五边形.getDian(x, AB), 五边形.getDian(x, CD), x, area); } else if (五边形.pointOnLine(五边形.getDian(x,AB),AB)&& 五边形.pointOnLine(五边形.getDian(x,DE),DE)) count2(A,E, 五边形.getDian(x,AB), 五边形.getDian(x,DE),x,area); else if (五边形.pointOnLine(五边形.getDian(x,AB),AB)&& 五边形.pointOnLine(五边形.getDian(x,EA),EA)) count1(A, 五边形.getDian(x,AB), 五边形.getDian(x,EA),x,area); //BC else if (五边形.pointOnLine(五边形.getDian(x,BC),BC)&& 五边形.pointOnLine(五边形.getDian(x,CD),CD)) count1(C, 五边形.getDian(x,BC), 五边形.getDian(x,CD),x,area); else if (五边形.pointOnLine(五边形.getDian(x,BC),BC)&& 五边形.pointOnLine(五边形.getDian(x,DE),DE)) count2(C,D, 五边形.getDian(x,BC), 五边形.getDian(x,DE),x,area); else if (五边形.pointOnLine(五边形.getDian(x,BC),BC)&& 五边形.pointOnLine(五边形.getDian(x,EA),EA)) count2(B,A, 五边形.getDian(x,BC), 五边形.getDian(x,EA),x,area); //CD else if (五边形.pointOnLine(五边形.getDian(x,CD),CD)&& 五边形.pointOnLine(五边形.getDian(x,DE),DE)) count1(D, 五边形.getDian(x,CD), 五边形.getDian(x,DE),x,area); else if (五边形.pointOnLine(五边形.getDian(x,CD),CD)&& 五边形.pointOnLine(五边形.getDian(x,EA),EA)) count2(D,E, 五边形.getDian(x,CD), 五边形.getDian(x,EA),x,area); else { count1(E, 五边形.getDian(x, DE), 五边形.getDian(x, EA), x, area); } } } public void count1(Point p, Point jp1, Point jp2, Line x, Double area){ double outArea1,outArea2; outArea1 = 0.5*x.lengthCount(p)*jp1.count(jp2); outArea2 = area-outArea1; if (outArea1<=outArea2){ System.out.print("2 "+ 五边形.change(outArea1)+" "+ 五边形.change(outArea2)); } else System.out.print("2 "+ 五边形.change(outArea2)+" "+ 五边形.change(outArea1)); } public void count2(Point p1, Point p2, Point jp1, Point jp2, Line x, Double area){ Line l =new Line(jp1,p2); l.abcCount(jp1,p2); double outArea1,outArea2; outArea1 = 0.5*(x.lengthCount(p2)*jp1.count(jp2)+l.lengthCount(p1)*jp1.count(p2)); outArea2 = area - outArea1; if (outArea1<=outArea2){ System.out.print("2 "+ 五边形.change(outArea1)+" "+ 五边形.change(outArea2)); } else System.out.print("2 "+ 五边形.change(outArea2)+" "+ 五边形.change(outArea1)); } }
类图及复杂度:
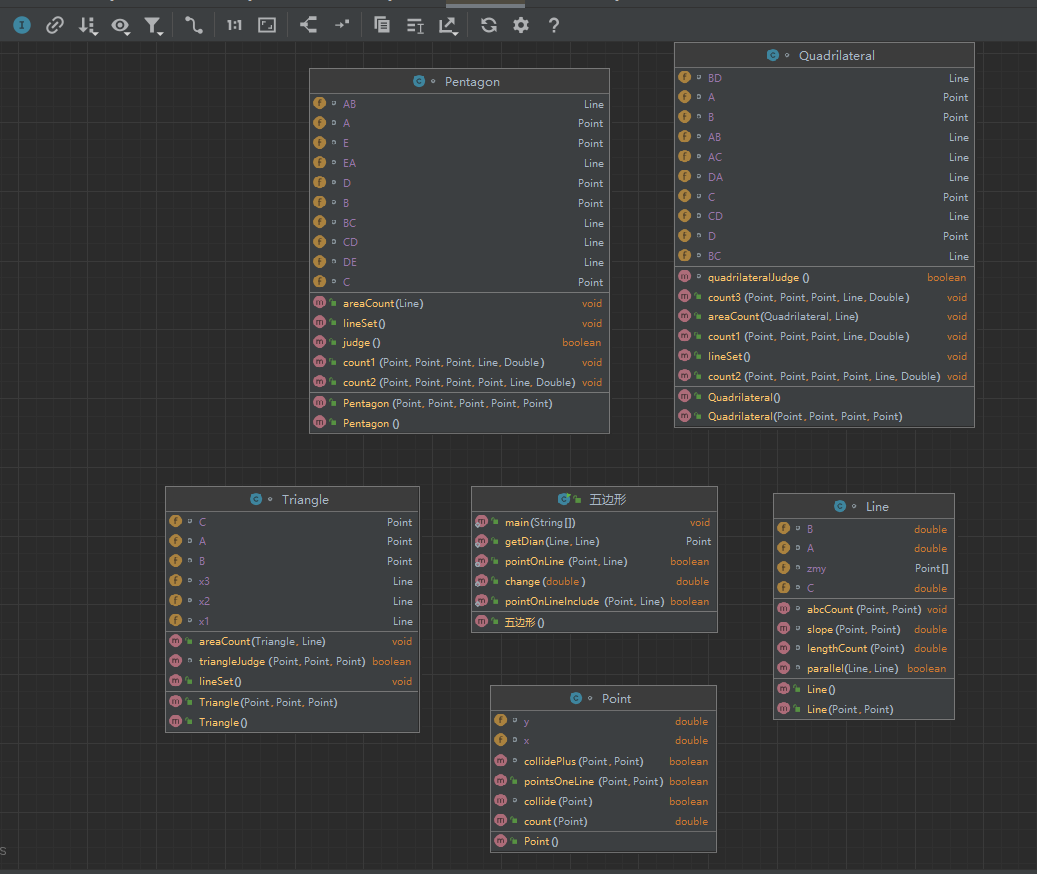
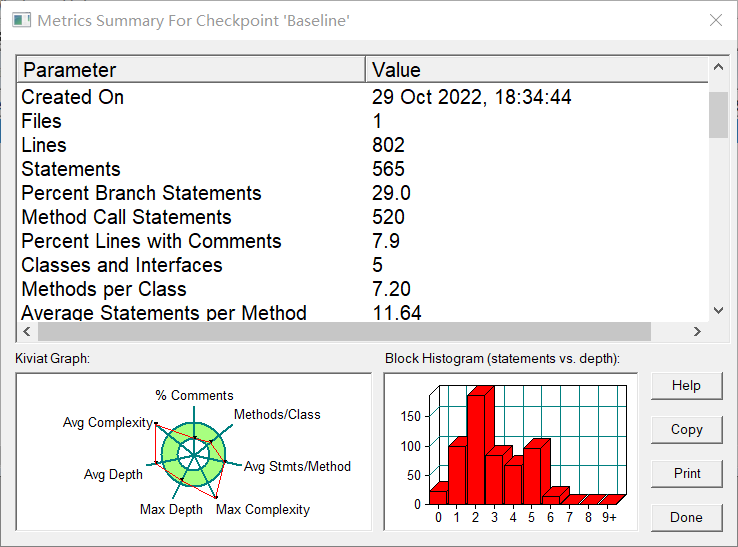
复杂度严重超标了啊喂
3. 点线形系列5-凸五边形的计算-2
题目要求:
用户输入一组选项和数据,进行与五边形有关的计算。
以下五边形顶点的坐标要求按顺序依次输入,连续输入的两个顶点是相邻顶点,第一个和最后一个输入的顶点相邻。
选项包括:
4:输入十个点坐标,前、后五个点分别构成一个凸多边形(三角形、四边形、五边形),判断它们两个之间是否存在包含关系(一个多边形有一条或多条边与另一个多边形重合,其他部分都包含在另一个多边形内部,也算包含)。
两者存在六种关系:1、分离(完全无重合点) 2、连接(只有一个点或一条边重合) 3、完全重合 4、被包含(前一个多边形在后一个多边形的内部)5、交错 6、包含(后一个多边形在前一个多边形的内部)。
各种关系的输出格式如下:
1、no overlapping area between the previous triangle/quadrilateral/ pentagon and the following triangle/quadrilateral/ pentagon
2、the previous triangle/quadrilateral/ pentagon is connected to the following triangle/quadrilateral/ pentagon
3、the previous triangle/quadrilateral/ pentagon coincides with the following triangle/quadrilateral/ pentagon
4、the previous triangle/quadrilateral/ pentagon is inside the following triangle/quadrilateral/ pentagon
5、the previous triangle/quadrilateral/ pentagon is interlaced with the following triangle/quadrilateral/ pentagon
6、the previous triangle/quadrilateral/ pentagon contains the following triangle/quadrilateral/ pentagon
5:输入十个点坐标,前、后五个点分别构成一个凸多边形(三角形、四边形、五边形),输出两个多边形公共区域的面积。注:只考虑每个多边形被另一个多边形分割成最多两个部分的情况,不考虑一个多边形将另一个分割成超过两个区域的情况。
6:输入六个点坐标,输出第一个是否在后五个点所构成的多边形(限定为凸多边形,不考虑凹多边形),的内部(若是五边形输出in the pentagon/outof the pentagon,若是四边形输出in the quadrilateral/outof the quadrilateral,若是三角形输出in the triangle/outof the triangle)。输入入错存在冗余点要排除,冗余点的判定方法见选项5。如果点在多边形的某条边上,输出"on the triangle/on the quadrilateral/on the pentagon"。
以上4、5、6选项输入的五个点坐标可能存在冗余,假设多边形一条边上两个端点分别是x、y,边线中间有一点z,另一顶点s:
1)符合要求的输入:顶点重复或者z与xy都相邻,如:x x y s、x z y s、x y x s、s x y y。此时去除冗余点,保留一个x、一个y。
2) 不符合要求的输入:z不与xy都相邻,如:z x y s、x z s y、x s z y
题目分析:
这题,因为是在是太难,以及当时我没有留出足够多的时间来写,一二题都十分摆烂地随便写了点,第三题倒是参照之前的方法进行分析后最后得出相应答案。
代码及注释:
package 博客2C; import java.math.BigDecimal; import java.util.Scanner; public class 五边形2 { public static void main(String[] args) { Scanner sc = new Scanner(System.in); Point[] points = new Point[10]; int judge = 1, judge2 = 1;//初始化错误输入判断数 String zz = "^[+-]?(0|(0\\.\\d+)?|[1-9]\\d*(\\.\\d+)?)$";//正则表达式 String input = sc.nextLine();//接收输入 if ((input.charAt(0) != '4' && input.charAt(0) != '5' && input.charAt(0) != '6' )|| input.charAt(1) != ':') judge = 0;//当开头不满足“(1~3):”格式时,给判断数置0 String text = input.substring(2);//去除开头 String[] zmy = text.split(" ");//按照空格分割字符串 for (int z = 0; z < zmy.length; z++) { String[] zsh = zmy[z].split(",");//按照,分割字符串 if (zsh.length != 2) {//当坐标格式不为x,x时即有多余成分(such as: ,,)判断数置0 judge2 = 0; break; } if (!zsh[0].matches(zz) || !zsh[1].matches(zz)) {//当子字符串格式不匹配时,判断数置0 judge2 = 0; break; } Point a = new Point(); points[z] = a; points[z].x = Double.parseDouble(zsh[0]); points[z].y = Double.parseDouble(zsh[1]); } if (judge == 0) {//错误输入1 System.out.print("Wrong Format"); } else if (judge2 == 0) {//错误输入二 System.out.print("Wrong Format"); } else if ((input.charAt(0) == '4' || input.charAt(0) == '5') && zmy.length != 10 || (input.charAt(0) == '6' && zmy.length != 6) ) { //选项和输入的点的个数不匹配时 System.out.print("wrong number of points"); } else { if (input.charAt(0)=='4'){//4:0,0 6,0 8,0 7,3 6,6 4,0 6,0 12,0 11,3 10,6 if (points[0].x==0&&points[1].x==6&&points[2].x==7&&points[3].x==8&&points[5].x==0) System.out.print("the previous pentagon coincides with the following pentagon"); else if (points[0].x==0&&points[1].x==6&&points[2].x==8&&points[3].x==8&&points[5].x==0) System.out.print("the previous quadrilateral contains the following pentagon"); else if (points[0].x==0&&points[1].x==5&&points[2].x==6&&points[3].x==8&&points[5].x==0) System.out.print("the previous quadrilateral is inside the following pentagon"); else if (points[0].x==0&&points[1].x==-3&&points[2].x==-6&&points[3].x==-8&&points[5].x==0) System.out.print("the previous quadrilateral is connected to the following pentagon"); else if (points[0].x==0&&points[1].x==6&&points[2].x==7&&points[3].x==8&&points[5].x==8) System.out.println("the previous pentagon is interlaced with the following triangle"); else if (points[0].x==0&&points[1].x==6&&points[2].x==8&&points[3].x==8&&points[5].x==1) System.out.println("the previous quadrilateral is interlaced with the following pentagon"); else if (points[0].x==0&&points[1].x==6&&points[2].x==8&&points[3].x==7&&points[5].x==6) System.out.println("the previous triangle is interlaced with the following triangle"); else System.out.println("the previous triangle is interlaced with the following triangle"); } else if (input.charAt(0)=='5'){ if (points[1].x==6) System.out.println("27.0"); else System.out.println("4.0"); } else{ int mark = 6; int sign; int y = 0; Point p = new Point(); p = points[0]; Point [] pointsUnRe = new Point[5]; for (int z = 1 ; z < mark ; z++){//去除重复点 sign = 1 ; if (z==1) {//第一个点无脑放 pointsUnRe[y] = points[z]; y++; } else{ for (int m = 0 ; m < y; m++){//接下来的每一个都和无重复点数组里已有的进行比较 if (points[z].collide(pointsUnRe[m]))//如果重复,则弃置 sign = 0; } if (sign == 1){ pointsUnRe[y] = points[z];//反之也放入无重复点数组 y++; } } } int length = y;//可用点数组的实际长度 if (length<3||length>5) System.out.print("not a polygon"); else if (length==3){//3:0,0 2,2 0,0 0,4 4,0 0,4 4,0 Triangle tri = new Triangle(pointsUnRe[0],pointsUnRe[1],pointsUnRe[2]); tri.lineSet(); if (!tri.triangleJudge(tri.A,tri.B,tri.C)) System.out.print("not a polygon"); else tri.check(p); } else if (length==4){//3:0,10 10,0 0,0 10,0 10,10 0,10 10,0 Quadrilateral qua = new Quadrilateral(pointsUnRe[0],pointsUnRe[1],pointsUnRe[2],pointsUnRe[3]); qua.lineSet(); if (!qua.quadrilateralJudge()) System.out.print("not a polygon"); else qua.check(p); } else {//3:10,0 120,0 0,0 6,0 7,0 8,0 8,6 int tMark = 0; int qMark = 0; int pMark = 0; int oMark = 0; Triangle tri = new Triangle(); Quadrilateral qua = new Quadrilateral(); Pentagon pen = new Pentagon(pointsUnRe[0],pointsUnRe[1],pointsUnRe[2],pointsUnRe[3],pointsUnRe[4]); pen.lineSet(); Line AC = new Line(pen.A,pen.C); AC.abcCount(pen.A,pen.C); Line BD = new Line(pen.B,pen.D); BD.abcCount(pen.B,pen.D); Line CE = new Line(pen.C,pen.E); CE.abcCount(pen.C,pen.E); Line DA = new Line(pen.D,pen.A); DA.abcCount(pen.D,pen.A); Line EB = new Line(pen.E,pen.B); EB.abcCount(pen.E,pen.B); if (pen.B.x* AC.A+pen.B.y* AC.B+ AC.C==0&&pointOnLine(pen.B,AC)&&pen.D.x* CE.A+pen.D.y* CE.B+CE.C==0&&pointOnLine(pen.D,CE)){ Triangle triangle = new Triangle(pen.A,pen.C,pen.E);//A B C||D E A tri = triangle; tMark = 1; } else if (pen.C.x* BD.A+pen.C.y* BD.B+ BD.C==0&&pointOnLine(pen.C,BD)&&pen.A.x* EB.A+pen.A.y* EB.B+EB.C==0&&pointOnLine(pen.A,EB)){ Triangle triangle = new Triangle(pen.B,pen.D,pen.E);//B C D||E A B tri = triangle; tMark = 1; } else if (pen.C.x* BD.A+pen.C.y* BD.B+ BD.C==0&&pointOnLine(pen.C,BD)&&pen.E.x* DA.A+pen.E.y* DA.B+DA.C==0&&pointOnLine(pen.E,DA)){ Triangle triangle = new Triangle(pen.A,pen.B,pen.D);//B C D||D E A tri = triangle; tMark = 1; } else if (pen.B.x* AC.A+pen.B.y* AC.B+ AC.C==0&&pointOnLine(pen.B,AC)&&pen.E.x* DA.A+pen.E.y* DA.B+DA.C==0&&pointOnLine(pen.E,DA)){ Triangle triangle = new Triangle(pen.A,pen.C,pen.D);//A B C||D E A tri = triangle; tMark = 1; } else if (pen.D.x* CE.A+pen.D.y* CE.B+ CE.C==0&&pointOnLine(pen.D,CE)&&pen.A.x* EB.A+pen.A.y* EB.B+EB.C==0&&pointOnLine(pen.A,EB)){ Triangle triangle = new Triangle(pen.B,pen.C,pen.E);//C D E||E A B tri = triangle; tMark = 1; } else if (pen.B.x*DA.A+pen.B.y*DA.B+DA.C==0&&pointOnLine(pen.B,DA)&&pen.C.x*DA.A+pen.C.y*DA.B+DA.C==0&&pointOnLine(pen.C,DA)){ Triangle triangle = new Triangle(pen.A,pen.D,pen.E); tri = triangle; tMark = 1; } else if (pen.A.x*EB.A+pen.A.y*EB.B+ EB.C==0&&pointOnLine(pen.A,EB)){ Quadrilateral quadrilateral = new Quadrilateral(pen.B,pen.C,pen.D,pen.E); qua = quadrilateral; qMark = 1; } else if (pen.B.x*AC.A+pen.B.y*AC.B+ AC.C==0&&pointOnLine(pen.B,AC)){ Quadrilateral quadrilateral = new Quadrilateral(pen.A,pen.C,pen.D,pen.E); qua = quadrilateral; qMark = 1; } else if (pen.C.x*BD.A+pen.C.y*BD.B+ BD.C==0&&pointOnLine(pen.C,BD)){ Quadrilateral quadrilateral = new Quadrilateral(pen.A,pen.B,pen.D,pen.E); qua = quadrilateral; qMark = 1; } else if (pen.D.x*CE.A+pen.D.y*CE.B+ CE.C==0&&pointOnLine(pen.D,CE)){ Quadrilateral quadrilateral = new Quadrilateral(pen.A,pen.B,pen.C,pen.E); qua = quadrilateral; qMark = 1; }//6:8.01,0 0,0 6,0 7,0 8,0 8,6 else if (pen.E.x*DA.A+pen.E.y*DA.B+ DA.C==0&&pointOnLine(pen.E,DA)){ Quadrilateral quadrilateral = new Quadrilateral(pen.A,pen.B,pen.C,pen.D); qua = quadrilateral; qMark = 1; } else if (pen.judge()) pMark = 1; else { oMark = 1; System.out.print("not a polygon"); } if (oMark==0) { if (tMark == 1 && qMark == 0 && pMark == 0) { tri.lineSet(); tri.check(p); } else if (tMark == 0 && qMark == 1 && pMark == 0) { qua.lineSet(); qua.check(p); } else if (tMark==0&&qMark==0&&pMark==1){ pen.check(p); } else System.out.print("not a polygon"); } } } } } public static boolean pointOnLine(Point p,Line l ){//不含端点 if (l.A==0){ if (p.x>Math.min(l.zmy[0].x,l.zmy[1].x)&&p.x<Math.max(l.zmy[0].x,l.zmy[1].x)) return true; else return false; } else if (l.B==0){ if (p.y>Math.min(l.zmy[0].y,l.zmy[1].y)&&p.y<Math.max(l.zmy[0].y,l.zmy[1].y)) return true; else return false; } else { if ((p.x > Math.min(l.zmy[0].x, l.zmy[1].x) && p.x < Math.max(l.zmy[0].x, l.zmy[1].x)) && (p.y > Math.min(l.zmy[0].y, l.zmy[1].y) && p.y < Math.max(l.zmy[0].y, l.zmy[1].y))) return true;//点在线段上 else return false; } } public static boolean pointOnLineInclude(Point p,Line l ){//含端点 if (l.A==0){ if (p.x>=Math.min(l.zmy[0].x,l.zmy[1].x)&&p.x<=Math.max(l.zmy[0].x,l.zmy[1].x)) return true; else return false; } else if (l.B==0){ if (p.y>=Math.min(l.zmy[0].y,l.zmy[1].y)&&p.y<=Math.max(l.zmy[0].y,l.zmy[1].y)) return true; else return false; } else { if ((p.x >= Math.min(l.zmy[0].x, l.zmy[1].x) && p.x <= Math.max(l.zmy[0].x, l.zmy[1].x)) && (p.y >= Math.min(l.zmy[0].y, l.zmy[1].y) && p.y <= Math.max(l.zmy[0].y, l.zmy[1].y))) return true;//点在线段上 else return false; } } public static Point getDian(Line x, Line y) {//计算交点 Point re = new Point(); re.x = (y.C * x.B - x.C * y.B) / (x.A * y.B - y.A * x.B); re.y = (x.C * y.A - y.C * x.A) / (x.A * y.B - y.A * x.B); return re; } public static double change(double d) {//转化为三位小数 double d1; BigDecimal big = new BigDecimal(d); d1 = big.setScale(3, BigDecimal.ROUND_HALF_UP).doubleValue(); return d1; } } class Point { double x, y; public Point() { } public double count(Point a) {//求两点之间距离 double fin; fin = Math.sqrt(Math.pow((a.x - this.x), 2) + Math.pow((a.y - this.y), 2)); return fin; } boolean collide(Point b) {//求重合点 if (this.x == b.x && this.y == b.y) return true; else return false; } boolean collidePlus(Point a, Point b){ if (this.collide(a)&&this.collide(b)) return true; else return false; } public boolean pointsOneLine(Point p1 , Point p2){ Line l = new Line(p1,p2); l.abcCount(p1,p2); if (x* l.A+y* l.B+ l.C==0) return true; else return false; } } class Line { Point[] zmy = new Point[2]; double A, B, C; public Line() { } public Line(Point a, Point b) { zmy[0] = a; zmy[1] = b; } double slope(Point a, Point b) {//求斜率 double sSlope; if (b.x == a.x) sSlope = 1000000000; else { sSlope = (b.y - a.y) / (b.x - a.x); } return sSlope; } void abcCount(Point a, Point b) {//计算直线一般式ABC if (b.y-a.y==0) { this.A = 0; this.B = 1; this.C = -b.y; } else if (a.x - b.x==0){ this.A = 1; this.B = 0; this.C = -a.x; } else { this.A = b.y - a.y; this.B = a.x - b.x; this.C = b.x * a.y - b.y * a.x; } } boolean parallel(Line x1, Line x2) {//平行线判断 double slope1, slope2; slope1 = x1.slope(x1.zmy[0], x1.zmy[1]); slope2 = x1.slope(x2.zmy[0], x2.zmy[1]); if (slope1 == slope2)//斜率相等 return true; else return false; } double lengthCount(Point a) {//求点a到此直线的距离 double length; length = Math.abs(this.A * a.x + this.B * a.y + this.C) / Math.sqrt(Math.pow(this.A, 2) + Math.pow(this.B, 2)); return length; } } class Triangle{ Point A, B, C; Line x1, x2, x3; public Triangle(){ } public Triangle(Point p1,Point p2,Point p3){ A = p1; B = p2; C = p3; } boolean triangleJudge(Point A, Point B, Point C) {//判断三角形是否合法 int judge = 1; Line x1 = new Line(); x1.A = B.y - A.y; x1.B = A.x - B.x; x1.C = B.x * A.y - B.y * A.x; if (x1.A * C.x + x1.B * C.y + x1.C == 0)//三点共线时不能构成三角形 judge = 0; if (judge == 1)//如果是合法三角形 return true; else return false; } public void lineSet(){ x1 = new Line(A,B); x2 = new Line(A,C); x3 = new Line(B,C); x1.abcCount(A,B); x2.abcCount(A,C); x3.abcCount(B,C); } public void areaCount(Triangle tria , Line x){//3:0,0 2,2 0,0 0,4 4,0 0,4 4,0 if (((x.A*tria.A.x+ x.B*tria.A.y+ x.C==0)&&(x.A*tria.B.x+ x.B*tria.B.y+ x.C==0))||((x.A*tria.C.x+ x.B*tria.C.y+ x.C==0)&&(x.A*tria.B.x+ x.B*tria.B.y+ x.C==0))||((x.A*tria.A.x+ x.B*tria.A.y+ x.C==0)&&(x.A*tria.C.x+ x.B*tria.C.y+ x.C==0))){ //如果顶点带入直线x方程成立,说明直线和边重合 System.out.print("The line is coincide with one of the lines"); } else {//当x和三条边都没有交点时 if (!五边形2.pointOnLine(五边形2.getDian(x,x1),x1)&&(!五边形2.pointOnLine(五边形2.getDian(x,x2),x2))&&(!五边形2.pointOnLine(五边形2.getDian(x,x3),x3))&&tria.A.x*x.A+tria.A.y*x.B+x.C!=0&&tria.B.x*x.A+tria.B.y*x.B+x.C!=0&&tria.C.x*x.A+tria.C.y*x.B+x.C!=0){ System.out.print("0"); }//当只有一个交点时 else if ((x.A * tria.A.x + x.B * tria.A.y + x.C==0&&!五边形2.pointOnLine(五边形2.getDian(x,x3),x3))||(x.A * tria.B.x + x.B * tria.B.y + x.C==0&&!五边形2.pointOnLine(五边形2.getDian(x,x2),x2))|| (x.A * tria.C.x + x.B * tria.C.y + x.C==0&&!五边形2.pointOnLine(五边形2.getDian(x,x1),x1))){ System.out.print("1"); } else {//当有两个交点时 double tArea = Math.sqrt(Math.pow(tria.A.x-tria.B.x,2)+Math.pow(tria.A.y-tria.B.y,2))*tria.x1.lengthCount(tria.C)/2; double area1,area2; double l1,l2,l3; Point dian1 = new Point(); Point dian2 = new Point(); Point dian3 = new Point(); int jJudge = 1; if (x.A * tria.A.x + x.B * tria.A.y + x.C==0){//过A点将三角形分成两个三角形 dian1 = tria.A;//交点1为A点 dian2 = 五边形2.getDian(x, tria.x3);//计算交点2 l1 = Math.sqrt(Math.pow(dian1.x-dian2.x,2)+Math.pow(dian1.y-dian2.y,2));//计算底边长度 l2 = x.lengthCount(tria.B);//计算B到直线x的距离 l3 = x.lengthCount(tria.C);//计算C到直线x的距离 area1 = l1*l2/2; area2 = l1*l3/2; jJudge = 0; if (area2>area1){ System.out.print("2 "+ 五边形2.change(area1)+" "+ 五边形2.change(area2)); } else System.out.print("2 "+ 五边形2.change(area2)+" "+ 五边形2.change(area1)); } if (x.A * tria.B.x + x.B * tria.B.y + x.C==0){//过B点将三角形分成两个三角形 dian1 = tria.B; dian2 = 五边形2.getDian(x, tria.x2); l1 = Math.sqrt(Math.pow(dian1.x-dian2.x,2)+Math.pow(dian1.y-dian2.y,2)); l2 = x.lengthCount(tria.C); l3 = x.lengthCount(tria.A); area1 = l1*l2/2; area2 = l1*l3/2; jJudge = 0; if (area2>area1){ System.out.print("2 "+ 五边形2.change(area1)+" "+ 五边形2.change(area2)); } else System.out.print("2 "+ 五边形2.change(area2)+" "+ 五边形2.change(area1)); } if (x.A * tria.C.x + x.B * tria.C.y + x.C==0){////过C点将三角形分成两个三角形 dian1 = tria.C; dian2 = 五边形2.getDian(x, tria.x1); l1 = Math.sqrt(Math.pow(dian1.x-dian2.x,2)+Math.pow(dian1.y-dian2.y,2)); l2 = x.lengthCount(tria.B); l3 = x.lengthCount(tria.A); area1 = l1*l2/2; area2 = l1*l3/2; jJudge = 0; if (area2>area1){ System.out.print("2 "+ 五边形2.change(area1)+" "+ 五边形2.change(area2)); } else System.out.print("2 "+ 五边形2.change(area2)+" "+ 五边形2.change(area1)); } //当直线x和某条边的交点不在三角形上时,则两个交点和该边相对顶点会构成一个三角形(如直线和边AB的交点不在三角形上,则与边AC、BC相交与点E、F,此时CEF是一个三角形) // 此时则可通过计算该边相对顶点到直线的距离计算出其中一个划分后面积,再拿总面积减去该部分得到剩下的面积,下面的代码就是依此编写的 if (!五边形2.pointOnLine(五边形2.getDian(x,x1),x1)&&jJudge!=0){//直线与x1的交点不在三角形的边上 dian1 = 五边形2.getDian(x, tria.x2); dian2 = 五边形2.getDian(x, tria.x3); l1 = Math.sqrt(Math.pow(dian1.x-dian2.x,2)+Math.pow(dian1.y-dian2.y,2));//计算两个交点的距离 l2 = x.lengthCount(tria.C);//计算顶点C到直线的距离 area1 = l2*l1/2; area2 = tArea - area1; if (area2>area1){ System.out.print("2 "+ 五边形2.change(area1)+" "+ 五边形2.change(area2)); } else System.out.print("2 "+ 五边形2.change(area2)+" "+ 五边形2.change(area1)); } if (!五边形2.pointOnLine(五边形2.getDian(x,x2),x2)&&jJudge!=0){ dian1 = 五边形2.getDian(x, tria.x1); dian2 = 五边形2.getDian(x, tria.x3); l1 = Math.sqrt(Math.pow(dian1.x-dian2.x,2)+Math.pow(dian1.y-dian2.y,2)); l2 = x.lengthCount(tria.B); area1 = l2*l1/2; area2 = tArea - area1; if (area2>area1){ System.out.print("2 "+ 五边形2.change(area1)+" "+ 五边形2.change(area2)); } else System.out.print("2 "+ 五边形2.change(area2)+" "+ 五边形2.change(area1)); } if (!五边形2.pointOnLine(五边形2.getDian(x,x3),x3)&&jJudge!=0){ dian1 = 五边形2.getDian(x, tria.x2); dian2 = 五边形2.getDian(x, tria.x1); l1 = Math.sqrt(Math.pow(dian1.x-dian2.x,2)+Math.pow(dian1.y-dian2.y,2)); l2 = x.lengthCount(tria.A); area1 = l2*l1/2; area2 = tArea - area1; if (area2>area1){ System.out.print("2 "+ 五边形2.change(area1)+" "+ 五边形2.change(area2)); } else System.out.print("2 "+ 五边形2.change(area2)+" "+ 五边形2.change(area1)); } } } } public void check(Point p){ if ((p.x*x1.A+ p.y* x1.B+x1.C==0&& 五边形2.pointOnLineInclude(p,x1))||(p.x*x2.A+ p.y* x2.B+x2.C==0&& 五边形2.pointOnLineInclude(p,x2))||(p.x*x3.A+ p.y* x3.B+x3.C==0&& 五边形2.pointOnLineInclude(p,x3))) System.out.println("on the triangle"); else { double area1, area2; area1 = 0.5 * x3.lengthCount(A) * B.count(C); area2 = 0.5 * (x1.lengthCount(p) * A.count(B) + x2.lengthCount(p) * A.count(C) + x3.lengthCount(p) * B.count(C)); if (Math.abs(area1 - area2) < 0.00001) System.out.print("in the triangle"); else System.out.print("outof the triangle"); } } } class Quadrilateral{ Point A, B, C, D; Line AB, BC, CD, DA, AC, BD; public Quadrilateral(){ } public Quadrilateral(Point A,Point B,Point C, Point D){ this.A = A; this.B = B; this.C = C; this.D = D; } public void lineSet() {//初始化四边形各边 AB = new Line(A, B); BC = new Line(B, C); CD = new Line(C, D); DA = new Line(D, A); AC = new Line(A, C); BD = new Line(B, D); AB.abcCount(A,B); BC.abcCount(B,C); CD.abcCount(C,D); DA.abcCount(D,A); AC.abcCount(A,C); BD.abcCount(B,D); } boolean quadrilateralJudge() {//判断四边形是否合法 if (A.pointsOneLine(B,C) || B.pointsOneLine(C,D) || A.pointsOneLine(C,D)|| A.pointsOneLine(B,D)) { return false; } lineSet(); if (!AB.parallel(AB, CD)) { Point p = new Point(); p = 五边形2.getDian(AB, CD); if (((p.x > Math.min(A.x, B.x) && p.x < Math.max(A.x, B.x)) || (p.y > Math.min(A.y,B.y) && p.y < Math.max(A.y, B.y)))&& ((p.x > Math.min(C.x, D.x) && p.x < Math.max(C.x, D.x)) || (p.y > Math.min(C.y, D.y) && p.y < Math.max(C.y, D.y)))) { return false; } } if (!DA.parallel(DA,BC)) { Point p = new Point(); p = 五边形2.getDian(DA, BC); if (((p.x > Math.min(A.x, D.x) && p.x < Math.max(A.x, D.x)) || (p.y > Math.min(A.y, D.y) && p.y < Math.max(A.y, D.y))) && ((p.x > Math.min(C.x, B.x) && p.x < Math.max(C.x, B.x)) || (p.y > Math.min(C.y, B.y) && p.y < Math.max(C.y,B.y)))) { return false; } } return true; } public void areaCount(Quadrilateral qua,Line x){ if ((x.A*qua.A.x+x.B*qua.A.y+x.C==0&&x.A*qua.B.x+x.B*qua.B.y+x.C==0)||(x.A*qua.C.x+x.B*qua.C.y+x.C==0&&x.A*qua.B.x+x.B*qua.B.y+x.C==0)|| (x.A*qua.C.x+x.B*qua.C.y+x.C==0&&x.A*qua.D.x+x.B*qua.D.y+x.C==0)||(x.A*qua.A.x+x.B*qua.A.y+x.C==0&&x.A*qua.D.x+x.B*qua.D.y+x.C==0)) System.out.print("The line is coincide with one of the lines"); else if ((x.parallel(x,AB)||!五边形2.pointOnLineInclude(五边形2.getDian(x,AB),AB))&& (x.parallel(x,BC)||!五边形2.pointOnLineInclude(五边形2.getDian(x,BC),BC))&& (x.parallel(x,CD)||!五边形2.pointOnLineInclude(五边形2.getDian(x,CD),CD))&& (x.parallel(x,DA)||!五边形2.pointOnLineInclude(五边形2.getDian(x,DA),DA))) System.out.print("0"); else if ( (x.A*A.x+x.B*A.y+x.C==0&&(x.parallel(x,BC)||!五边形2.pointOnLineInclude(五边形2.getDian(x,BC),BC))&&(x.parallel(x,CD)||!五边形2.pointOnLineInclude(五边形2.getDian(x,CD),CD)))|| (x.A*B.x+x.B*B.y+x.C==0&&(x.parallel(x,CD)||!五边形2.pointOnLineInclude(五边形2.getDian(x,CD),CD))&&(x.parallel(x,DA)||!五边形2.pointOnLineInclude(五边形2.getDian(x,DA),DA)))|| (x.A*C.x+x.B*C.y+x.C==0&&(x.parallel(x,DA)||!五边形2.pointOnLineInclude(五边形2.getDian(x,DA),DA))&&(x.parallel(x,AB)||!五边形2.pointOnLineInclude(五边形2.getDian(x,AB),AB)))|| (x.A*D.x+x.B*D.y+x.C==0&&(x.parallel(x,AB)||!五边形2.pointOnLineInclude(五边形2.getDian(x,AB),AB))&&(x.parallel(x,BC)||!五边形2.pointOnLineInclude(五边形2.getDian(x,BC),BC))) ) System.out.print("1"); else {//3:0,10 10,0 0,0 10,0 10,10 0,10 10,0 //过某一端点 Double area = 0.5*(AC.lengthCount(B)*A.count(C)+AC.lengthCount(D)*A.count(C)); if (x.A*A.x+x.B*A.y+x.C==0&& 五边形2.pointOnLineInclude(五边形2.getDian(x,BC),BC)) count3(B,A, 五边形2.getDian(x,BC),x,area); else if (x.A*A.x+x.B*A.y+x.C==0&& 五边形2.pointOnLineInclude(五边形2.getDian(x,CD),CD)) count3(D,A, 五边形2.getDian(x,CD),x,area); else if (x.A*B.x+x.B*B.y+x.C==0&& 五边形2.pointOnLineInclude(五边形2.getDian(x,CD),CD)) count3(C,B, 五边形2.getDian(x,CD),x,area); else if (x.A*B.x+x.B*B.y+x.C==0&& 五边形2.pointOnLineInclude(五边形2.getDian(x,DA),DA)) count3(A,B, 五边形2.getDian(x,DA),x,area); else if (x.A*C.x+x.B*C.y+x.C==0&& 五边形2.pointOnLineInclude(五边形2.getDian(x,DA),DA)) count3(D,C, 五边形2.getDian(x,DA),x,area); else if (x.A*C.x+x.B*C.y+x.C==0&& 五边形2.pointOnLineInclude(五边形2.getDian(x,AB),AB)) count3(B,C, 五边形2.getDian(x,AB),x,area); else if (x.A*D.x+x.B*D.y+x.C==0&& 五边形2.pointOnLineInclude(五边形2.getDian(x,AB),AB)) count3(A,D, 五边形2.getDian(x,AB),x,area); else if (x.A*D.x+x.B*D.y+x.C==0&& 五边形2.pointOnLineInclude(五边形2.getDian(x,BC),BC)) count3(C,D, 五边形2.getDian(x,BC),x,area); //不过顶点 else if (!x.parallel(x,AB)&&!x.parallel(x,BC)&& 五边形2.pointOnLine(五边形2.getDian(x,AB),AB)&& 五边形2.pointOnLine(五边形2.getDian(x,BC),BC)) count1(B, 五边形2.getDian(x,AB), 五边形2.getDian(x,BC),x,area); else if (!x.parallel(x,BC)&&!x.parallel(x,CD)&& 五边形2.pointOnLine(五边形2.getDian(x,BC),BC)&& 五边形2.pointOnLine(五边形2.getDian(x,CD),CD)) count1(C, 五边形2.getDian(x,CD), 五边形2.getDian(x,BC),x,area); else if (!x.parallel(x,DA)&&!x.parallel(x,CD)&& 五边形2.pointOnLine(五边形2.getDian(x,DA),DA)&& 五边形2.pointOnLine(五边形2.getDian(x,CD),CD)) count1(D, 五边形2.getDian(x,DA), 五边形2.getDian(x,CD),x,area); else if (!x.parallel(x,DA)&&!x.parallel(x,AB)&& 五边形2.pointOnLine(五边形2.getDian(x,DA),DA)&& 五边形2.pointOnLine(五边形2.getDian(x,AB),AB)) count1(A, 五边形2.getDian(x,DA), 五边形2.getDian(x,AB),x,area); else if (!x.parallel(x,AB)&&!x.parallel(x,CD)&& 五边形2.pointOnLine(五边形2.getDian(x,AB),AB)&& 五边形2.pointOnLine(五边形2.getDian(x,CD),CD)) count2(A,D, 五边形2.getDian(x,AB), 五边形2.getDian(x,CD),x,area); else count2(B,A, 五边形2.getDian(x,BC), 五边形2.getDian(x,DA),x,area); } } public void count1(Point p1,Point jp1, Point jp2, Line x, Double area){ Double outArea1,outArea2; outArea1 = 0.5*x.lengthCount(p1) * jp1.count(jp2); outArea2 = area-outArea1; if (outArea1<=outArea2){ System.out.print("2 "+ 五边形2.change(outArea1)+" "+ 五边形2.change(outArea2)); } else System.out.print("2 "+ 五边形2.change(outArea2)+" "+ 五边形2.change(outArea1)); } public void count2(Point p1, Point p2,Point jp1, Point jp2, Line x, Double area){ Double outArea1,outArea2; Line l = new Line(p1,jp1); l.abcCount(p1,jp1); outArea1 = 0.5*(l.lengthCount(p2)*p1.count(jp1)+x.lengthCount(p2)*jp1.count(jp2)); outArea2 = area - outArea1; if (outArea1<=outArea2){ System.out.print("2 "+ 五边形2.change(outArea1)+" "+ 五边形2.change(outArea2)); } else System.out.print("2 "+ 五边形2.change(outArea2)+" "+ 五边形2.change(outArea1)); } public void count3(Point p, Point jp1, Point jp2, Line x, Double area){ Double outArea1,outArea2; outArea1 = 0.5*x.lengthCount(p)*jp1.count(jp2); outArea2 = area-outArea1; if (outArea1<=outArea2){ System.out.print("2 "+ 五边形2.change(outArea1)+" "+ 五边形2.change(outArea2)); } else System.out.print("2 "+ 五边形2.change(outArea2)+" "+ 五边形2.change(outArea1)); } public void check(Point p){//6:7.1,1 0,0 6,0 7,1 8,3 6,6 if ((AB.A*p.x+AB.B* p.y+AB.C==0&& 五边形2.pointOnLineInclude(p,AB))||(BC.A*p.x+BC.B* p.y+BC.C==0&& 五边形2.pointOnLineInclude(p,BC))||(CD.A*p.x+CD.B* p.y+CD.C==0&& 五边形2.pointOnLineInclude(p,CD))||(DA.A*p.x+DA.B* p.y+DA.C==0&& 五边形2.pointOnLineInclude(p,DA))) System.out.println("on the quadrilateral"); else { Double area1,area2; area1 = 0.5*( AC.lengthCount(B)*A.count(C) + AC.lengthCount(D)*A.count(C)); area2 = 0.5*(AB.lengthCount(p)*A.count(B)+BC.lengthCount(p)*B.count(C)+CD.lengthCount(p)*C.count(D)+DA.lengthCount(p)*D.count(A)); if (Math.abs(area1-area2)<0.00001) System.out.println("in the quadrilateral"); else System.out.println("outof the quadrilateral"); } } } class Pentagon{ Point A,B,C,D,E; Line AB,BC,CD,DE,EA; public Pentagon(){ } public Pentagon(Point A,Point B,Point C,Point D,Point E){ this.A = A; this.B = B; this.C = C; this.D = D; this.E = E; } public void lineSet(){ AB = new Line(A,B); BC = new Line(B,C); CD = new Line(C,D); DE = new Line(D,E); EA = new Line(E,A); AB.abcCount(A,B); BC.abcCount(B,C); CD.abcCount(C,D); DE.abcCount(D,E); EA.abcCount(E,A); } public boolean judge(){ if (A.collide(B)||A.collide(C)||A.collide(D)||A.collide(E)||B.collide(C)||B.collide(D)||B.collide(E)||C.collide(D)|| C.collide(E)||D.collide(E)){ return false; } else if (AB.parallel(AB,BC)||BC.parallel(BC,CD)||CD.parallel(CD,DE)||DE.parallel(DE,EA)||EA.parallel(EA,AB)){ return false; }//AB CD AB DE BC DE BC AE CD AE else if (((五边形2.pointOnLine(五边形2.getDian(AB,CD),AB)&& 五边形2.pointOnLine(五边形2.getDian(AB,CD),CD))&&!AB.parallel(AB,CD))|| ((五边形2.pointOnLine(五边形2.getDian(AB,DE),AB)&& 五边形2.pointOnLine(五边形2.getDian(AB,DE),DE))&&!AB.parallel(AB,DE))|| ((五边形2.pointOnLine(五边形2.getDian(BC,DE),BC)&& 五边形2.pointOnLine(五边形2.getDian(BC,DE),DE))&&!BC.parallel(BC,DE))|| ((五边形2.pointOnLine(五边形2.getDian(BC,EA),BC)&& 五边形2.pointOnLine(五边形2.getDian(BC,EA),EA))&&!BC.parallel(BC,EA))|| ((五边形2.pointOnLine(五边形2.getDian(EA,CD),CD)&& 五边形2.pointOnLine(五边形2.getDian(EA,CD),EA))&&!EA.parallel(CD,EA)) ) return false; else return true; } public void areaCount(Line x){ if ((x.A*A.x+x.B*A.y+x.C==0&&x.A*B.x+x.B*B.y+x.C==0)||(x.A*C.x+x.B*C.y+x.C==0&&x.A*B.x+x.B*B.y+x.C==0)|| (x.A*C.x+x.B*C.y+x.C==0&&x.A*D.x+x.B*D.y+x.C==0)||(x.A*D.x+x.B*D.y+x.C==0&&x.A*E.x+x.B*E.y+x.C==0)||(x.A*E.x+x.B*E.y+x.C==0&&x.A*A.x+x.B*A.y+x.C==0)) System.out.print("The line is coincide with one of the lines"); else if ((x.parallel(x,AB)||(!五边形2.pointOnLineInclude(五边形2.getDian(x,AB),AB)))&&(x.parallel(x,BC)||(!五边形2.pointOnLineInclude(五边形2.getDian(x,BC),BC)))&& (x.parallel(x,CD)||(!五边形2.pointOnLineInclude(五边形2.getDian(x,CD),CD)))&& (x.parallel(x,DE)||(!五边形2.pointOnLineInclude(五边形2.getDian(x,DE),DE)))&& (x.parallel(x,EA)||(!五边形2.pointOnLineInclude(五边形2.getDian(x,EA),EA)))) System.out.print("0"); else if ( (x.A*A.x+x.B+A.y+x.C==0&&(x.parallel(x,BC)||!五边形2.pointOnLineInclude(五边形2.getDian(x,BC),BC))&&(x.parallel(x,CD)||!五边形2.pointOnLineInclude(五边形2.getDian(x,CD),CD))&&(x.parallel(x,DE)||!五边形2.pointOnLineInclude(五边形2.getDian(x,DE),DE)))|| (x.A*B.x+x.B+B.y+x.C==0&&(x.parallel(x,CD)||!五边形2.pointOnLineInclude(五边形2.getDian(x,CD),CD))&&(x.parallel(x,DE)||!五边形2.pointOnLineInclude(五边形2.getDian(x,DE),DE))&&(x.parallel(x,EA)||!五边形2.pointOnLineInclude(五边形2.getDian(x,EA),EA)))|| (x.A*C.x+x.B+C.y+x.C==0&&(x.parallel(x,DE)||!五边形2.pointOnLineInclude(五边形2.getDian(x,DE),DE))&&(x.parallel(x,EA)||!五边形2.pointOnLineInclude(五边形2.getDian(x,EA),EA))&&(x.parallel(x,AB)||!五边形2.pointOnLineInclude(五边形2.getDian(x,AB),AB)))|| (x.A*D.x+x.B+D.y+x.C==0&&(x.parallel(x,EA)||!五边形2.pointOnLineInclude(五边形2.getDian(x,EA),EA))&&(x.parallel(x,AB)||!五边形2.pointOnLineInclude(五边形2.getDian(x,AB),AB))&&(x.parallel(x,BC)||!五边形2.pointOnLineInclude(五边形2.getDian(x,BC),BC)))|| (x.A*E.x+x.B+E.y+x.C==0&&(x.parallel(x,AB)||!五边形2.pointOnLineInclude(五边形2.getDian(x,AB),AB))&&(x.parallel(x,BC)||!五边形2.pointOnLineInclude(五边形2.getDian(x,BC),BC))&&(x.parallel(x,CD)||!五边形2.pointOnLineInclude(五边形2.getDian(x,CD),CD))) ) System.out.print("1"); else { double area; area = 0.5*(BC.lengthCount(A)*B.count(C)+CD.lengthCount(A)*C.count(D)+DE.lengthCount(A)*D.count(E)); //AB if (x.A*A.x+x.B*A.y+x.C==0&& 五边形2.pointOnLineInclude(五边形2.getDian(x,BC),BC)) count1(B,A, 五边形2.getDian(x,BC),x,area); else if (x.A*A.x+x.B*A.y+x.C==0&& 五边形2.pointOnLineInclude(五边形2.getDian(x,DE),DE)) count1(E,A, 五边形2.getDian(x,DE),x,area); else if (x.A*B.x+x.B*B.y+x.C==0&& 五边形2.pointOnLineInclude(五边形2.getDian(x,CD),CD)) count1(C,B, 五边形2.getDian(x,CD),x,area); else if (x.A*B.x+x.B*B.y+x.C==0&& 五边形2.pointOnLineInclude(五边形2.getDian(x,EA),EA)) count1(A,B, 五边形2.getDian(x,EA),x,area); else if (x.A*C.x+x.B*C.y+x.C==0&& 五边形2.pointOnLineInclude(五边形2.getDian(x,DE),DE)) count1(D,C, 五边形2.getDian(x,DE),x,area); else if (x.A*C.x+x.B*C.y+x.C==0&& 五边形2.pointOnLineInclude(五边形2.getDian(x,AB),AB)) count1(B,C, 五边形2.getDian(x,AB),x,area); else if (x.A*D.x+x.B*D.y+x.C==0&& 五边形2.pointOnLineInclude(五边形2.getDian(x,EA),EA)) count1(E,D, 五边形2.getDian(x,EA),x,area); else if (x.A*D.x+x.B*D.y+x.C==0&& 五边形2.pointOnLineInclude(五边形2.getDian(x,BC),BC)) count1(C,D, 五边形2.getDian(x,BC),x,area); else if (x.A*E.x+x.B*E.y+x.C==0&& 五边形2.pointOnLineInclude(五边形2.getDian(x,AB),AB)) count1(A,E, 五边形2.getDian(x,AB),x,area); else if (x.A*E.x+x.B*E.y+x.C==0&& 五边形2.pointOnLineInclude(五边形2.getDian(x,CD),CD)) count1(D,E, 五边形2.getDian(x,CD),x,area); else if (x.A*A.x+x.B*A.y+x.C==0&& 五边形2.pointOnLineInclude(五边形2.getDian(x,CD),CD)) count2(B,C,A, 五边形2.getDian(x,CD),x,area); else if (x.A*B.x+x.B*B.y+x.C==0&& 五边形2.pointOnLineInclude(五边形2.getDian(x,DE),DE)) count2(C,D,B, 五边形2.getDian(x,DE),x,area); else if (x.A*C.x+x.B*C.y+x.C==0&& 五边形2.pointOnLineInclude(五边形2.getDian(x,EA),EA)) count2(D,E,C, 五边形2.getDian(x,EA),x,area); else if (x.A*D.x+x.B*D.y+x.C==0&& 五边形2.pointOnLineInclude(五边形2.getDian(x,AB),AB)) count2(E,A,D, 五边形2.getDian(x,AB),x,area); else if (x.A*E.x+x.B*E.y+x.C==0&& 五边形2.pointOnLineInclude(五边形2.getDian(x,BC),BC)) count2(A,B,E, 五边形2.getDian(x,BC),x,area); else if (五边形2.pointOnLine(五边形2.getDian(x,AB),AB)&& 五边形2.pointOnLine(五边形2.getDian(x,BC),BC)) count1(B, 五边形2.getDian(x,AB), 五边形2.getDian(x,BC),x,area); else if (五边形2.pointOnLine(五边形2.getDian(x,AB),AB)&& 五边形2.pointOnLine(五边形2.getDian(x,CD),CD)) { count2(B, C, 五边形2.getDian(x, AB), 五边形2.getDian(x, CD), x, area); } else if (五边形2.pointOnLine(五边形2.getDian(x,AB),AB)&& 五边形2.pointOnLine(五边形2.getDian(x,DE),DE)) count2(A,E, 五边形2.getDian(x,AB), 五边形2.getDian(x,DE),x,area); else if (五边形2.pointOnLine(五边形2.getDian(x,AB),AB)&& 五边形2.pointOnLine(五边形2.getDian(x,EA),EA)) count1(A, 五边形2.getDian(x,AB), 五边形2.getDian(x,EA),x,area); //BC else if (五边形2.pointOnLine(五边形2.getDian(x,BC),BC)&& 五边形2.pointOnLine(五边形2.getDian(x,CD),CD)) count1(C, 五边形2.getDian(x,BC), 五边形2.getDian(x,CD),x,area); else if (五边形2.pointOnLine(五边形2.getDian(x,BC),BC)&& 五边形2.pointOnLine(五边形2.getDian(x,DE),DE)) count2(C,D, 五边形2.getDian(x,BC), 五边形2.getDian(x,DE),x,area); else if (五边形2.pointOnLine(五边形2.getDian(x,BC),BC)&& 五边形2.pointOnLine(五边形2.getDian(x,EA),EA)) count2(B,A, 五边形2.getDian(x,BC), 五边形2.getDian(x,EA),x,area); //CD else if (五边形2.pointOnLine(五边形2.getDian(x,CD),CD)&& 五边形2.pointOnLine(五边形2.getDian(x,DE),DE)) count1(D, 五边形2.getDian(x,CD), 五边形2.getDian(x,DE),x,area); else if (五边形2.pointOnLine(五边形2.getDian(x,CD),CD)&& 五边形2.pointOnLine(五边形2.getDian(x,EA),EA)) count2(D,E, 五边形2.getDian(x,CD), 五边形2.getDian(x,EA),x,area); else { count1(E, 五边形2.getDian(x, DE), 五边形2.getDian(x, EA), x, area); } } } public void count1(Point p, Point jp1, Point jp2, Line x, Double area){ double outArea1,outArea2; outArea1 = 0.5*x.lengthCount(p)*jp1.count(jp2); outArea2 = area-outArea1; if (outArea1<=outArea2){ System.out.print("2 "+ 五边形2.change(outArea1)+" "+ 五边形2.change(outArea2)); } else System.out.print("2 "+ 五边形2.change(outArea2)+" "+ 五边形2.change(outArea1)); } public void count2(Point p1, Point p2, Point jp1, Point jp2, Line x, Double area){ Line l =new Line(jp1,p2); l.abcCount(jp1,p2); double outArea1,outArea2; outArea1 = 0.5*(x.lengthCount(p2)*jp1.count(jp2)+l.lengthCount(p1)*jp1.count(p2)); outArea2 = area - outArea1; if (outArea1<=outArea2){ System.out.print("2 "+ 五边形2.change(outArea1)+" "+ 五边形2.change(outArea2)); } else System.out.print("2 "+ 五边形2.change(outArea2)+" "+ 五边形2.change(outArea1)); } public void check(Point p){ if ((AB.A*p.x+AB.B*p.y+AB.C==0&& 五边形2.pointOnLineInclude(p,AB))||(BC.A*p.x+BC.B*p.y+BC.C==0&& 五边形2.pointOnLineInclude(p,BC))||(CD.A*p.x+CD.B*p.y+CD.C==0&& 五边形2.pointOnLineInclude(p,CD))||(DE.A*p.x+DE.B*p.y+DE.C==0&& 五边形2.pointOnLineInclude(p,DE))||(EA.A*p.x+EA.B*p.y+EA.C==0&& 五边形2.pointOnLineInclude(p,EA))) System.out.println("on the pentagon"); else { Double area1,area2; area1 = 0.5*(BC.lengthCount(A)*B.count(C)+CD.lengthCount(A)*C.count(D)+DE.lengthCount(A)*D.count(E)); area2 = 0.5*(AB.lengthCount(p)*A.count(B)+BC.lengthCount(p)*C.count(B)+CD.lengthCount(p)*C.count(D)+DE.lengthCount(p)*D.count(E)+EA.lengthCount(p)*A.count(E)); if (Math.abs(area1-area2)<0.00001) System.out.println("in the pentagon"); else System.out.println("outof the pentagon"); } } }
类图及复杂度:
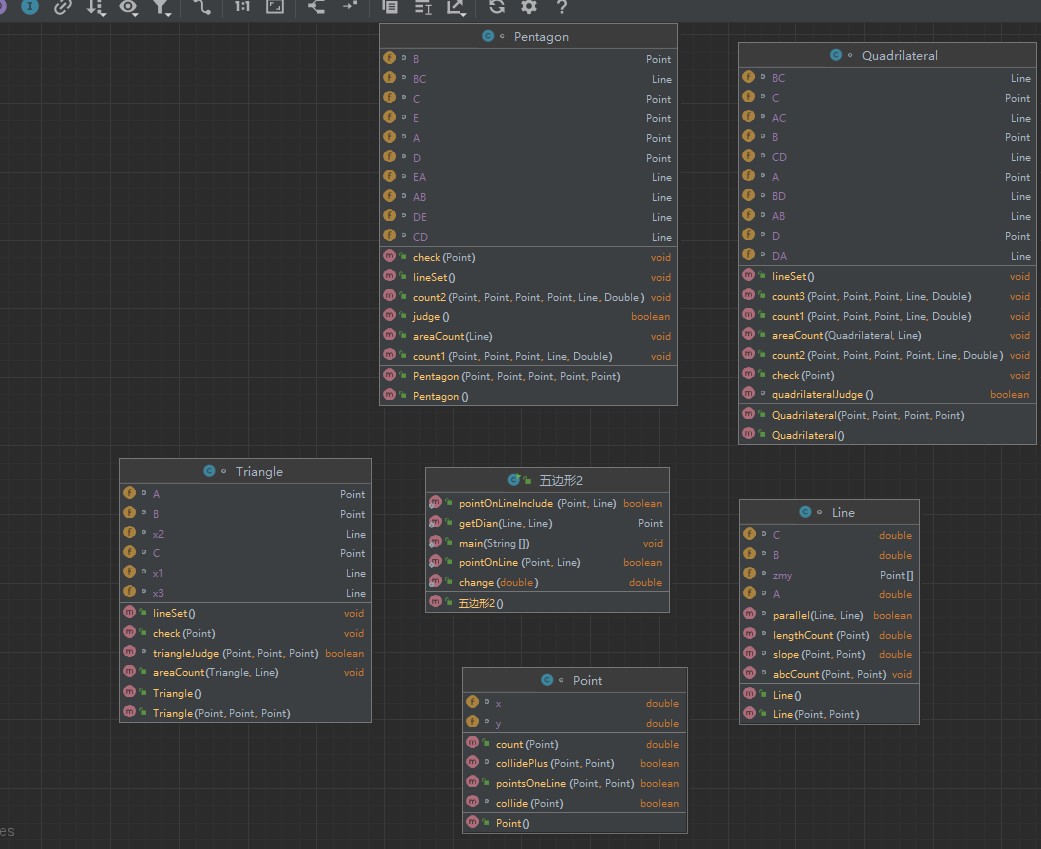
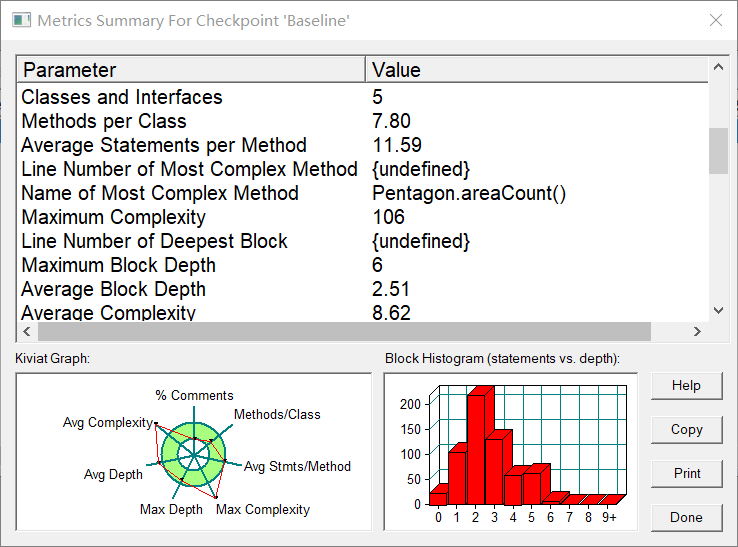
怎么才能降复杂度呢(疑似崩溃)
4.点线面问题再重构(容器类)
题目要求:
在“点与线(继承与多态)”题目基础上,对题目的类设计进行重构,增加容器类保存点、线、面对象,并对该容器进行相应增、删、遍历操作。
- 在原有类设计的基础上,增加一个GeometryObject容器类,其属性为
ArrayList<Element>类型的对象(若不了解泛型,可以不使用<Element>) - 增加该类的
add()方法及remove(int index)方法,其功能分别为向容器中增加对象及删除第index - 1(ArrayList中index>=0)个对象 - 在主方法中,用户循环输入要进行的操作(choice∈[0,4]),其含义如下:
- 1:向容器中增加Point对象
- 2:向容器中增加Line对象
- 3:向容器中增加Plane对象
- 4:删除容器中第index - 1个数据,若index数据非法,则无视此操作
- 0:输入结束
题目分析:
本题存在以下问题:
1.父类的创建及子类继承
我们在创建父类后,将子类共有的特性和方法设置好,再让各子类继承,可以达成多态的实现。
2.集合的使用
只要学习了集合的相应方法后根据题意在容器类中设置相应方法就能快速实现。
3.选项循环输入的判断
首先使用了do while方法和swich case方法得到输入的数据,但是其实在此基础上还可以加上对输入内容是否合法的判断,如输入选项是否在可用范围内,对应选项给出的输入是否符合要求。
代码及注释:
package 期中考试; import java.math.BigDecimal; import java.util.ArrayList; import java.util.Scanner; public class Work1 { public static void main(String[] args) { Scanner sc = new Scanner(System.in); int choice = sc.nextInt(); GeometryObject geometryObject = new GeometryObject(); while (choice!=0){ switch (choice){ case 1: { double x, y; x = sc.nextDouble(); y = sc.nextDouble(); Point point = new Point(x, y); geometryObject.add(point); break; } case 2:{ double x, y , x1 , y1; x = sc.nextDouble(); y = sc.nextDouble(); x1 = sc.nextDouble(); y1 = sc.nextDouble(); String color = sc.next(); Point p1 = new Point(x,y); Point p2 = new Point(x1,y1); Line line = new Line(p1,p2,color); geometryObject.add(line); break; } case 3:{ String color = sc.next(); Plane plane = new Plane(color); geometryObject.add(plane); break; } case 4:{ int index = sc.nextInt(); geometryObject.remove(index); break; } } choice = sc.nextInt(); } ArrayList<Element> arrayList = geometryObject.getList(); for (int z = 0 ; z < arrayList.size() ; z++) arrayList.get(z).display(); } } class Element{ public void display(){ } } class Point extends Element{ double x,y; public Point(){ } public Point(double x,double y){ this.x = x; this.y = y; } public double getX() { return x; } public void setX(double x) { this.x = x; } public double getY() { return y; } public void setY(double y) { this.y = y; } public void display(){ System.out.println("("+String.format("%.2f",this.x)+","+String.format("%.2f",this.y)+")"); } } class Line extends Element{ Point point1; Point point2; String color; public Line(){ } public Line(Point p1 ,Point p2, String color){ this.point1 = p1; this.point2 = p2; this.color = color; } public Point getPoint1() { return point1; } public void setPoint1(Point point1) { this.point1 = point1; } public Point getPoint2() { return point2; } public void setPoint2(Point point2) { this.point2 = point2; } public String getColor() { return color; } public void setColor(String color) { this.color = color; } public double getDistance(){ double distance; distance = Math.pow((Math.pow((point1.x-point2.x),2)+Math.pow((point1.y-point2.y),2)),0.5); return distance; } public void display(){ System.out.println("The line's color is:"+this.color); System.out.println("The line's begin point's Coordinate is:"); this.point1.display(); System.out.println("The line's end point's Coordinate is:"); this.point2.display(); System.out.println("The line's length is:"+String.format("%.2f",this.getDistance())); } } class Plane extends Element{ private String color; public Plane(){ } public Plane(String color){ this.color = color; } public String getColor() { return color; } public void setColor(String color) { this.color = color; } @Override public void display() { System.out.println("The Plane's color is:"+this.color); } } class GeometryObject{ ArrayList<Element> list = new ArrayList<>(); public GeometryObject(){ } public void add(Element element){ list.add(element); } public void remove(int index){ if (!(index >list.size()||index<0)) list.remove(index-1); } public ArrayList<Element> getList() { return list; } }
类图及复杂度:
还不错(理直气壮)
BUG及编写问题集合
1.空指针异常
最经典的错误,后面三道题都报过这种错,归根到底就是——没有new对象就直接使用了导致空指针异常,代码中(特别是三角形那题)涉及到很多对象的创建所以真的是老是报这个错误。这次也是一样,虽然比上次少了,但是还是有,每日一遍防止自己忘记。
2.输入异常
当输入不符合要求的内容时,如果没有提前做好异常处理则会报错,所以可以用到try catch来解决这一问题,对异常输入做好提前检测与修正。
总结
这次的三次作业依然是在上次作业的基础上进行了深化和复杂化,对于我们的代码编写能力和问题分析能力有了更深一步的要求。认真仔细,要站在用户角度上进行思考,我该怎样将这个程序描述好,又会有怎样的可能的问题会出现,出现了我怎样处理等等等等。
在此基础上慢慢细化一些细节部分,将代码功能补全,这个过程就需要我们发散思维,对可能出现的情况和问题在代码中给出相应的解决方案。最基本的比如说输入格式错误啊,除法计算时除数为0啊这些说出来都觉得平常但是代码中容易遗漏的东西。除此之外就是题目中隐含的一些要求和特殊情况,需要自己结合题意慢慢分析,再逐步完善。
而期中测试的三道题相对来说更简单,主要还是考察我们对子类父类关系和继承、多态的理解,如果这些知识掌握了那么想拿满分也非常容易。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号