第一次大作业blog
前言:
首先这是第一次写博客,谢邀,人很憔悴。回到正题,这次博客的内容是面向对象程序设计的前三次作业,第一第二次没什么好说的,都非常简单(看看一个个的都是满分我觉得懂的都懂)问题的处理过程以及代码编写都非常丝滑,除了第二次作业的第二题基本上没出现什么bug。总的来说就是属于让刚开始接触JAVA的学生练手的题目。画面转到第三次作业,这就非常惨烈了,题目中需要处理的问题相较于前两次多了不止一点点,三道题一环扣一环(所以其实后面代码编写的难度取决于你前面代码的完善程度)从点到线到三角形包括后两次作业的四边形和五边形,一个循序渐进的过程。代码编写方面呢,需要考虑的问题和情况非常非常多,所以编写过程也非常不顺利,具体分析会在下面给出。
但是总的来说,前三次作业并不算太难,仔细分析和多花时间也是能够拿到满分或者较高的分数的。
ps:对于题目的相关分析大多数放在代码的注释里了,就不额外陈述。
设计与分析
1.串口字符解析
题目要求:
RS232是串口常用的通信协议,在异步通信模式下,串口可以一次发送5~8位数据,收发双方之间没有数据发送时线路维持高电平,相当于接收方持续收到数据“1”(称为空闲位),发送方有数据发送时,会在有效数据(5~8位,具体位数由通信双方提前设置)前加上1位起始位“0”,在有效数据之后加上1位可选的奇偶校验位和1位结束位“1”。请编写程序,模拟串口接收处理程序,注:假定有效数据是8位,奇偶校验位采用奇校验。
题目分析:
依照题意将问题划分为以下几个方面:输入格式为0、1组成的长串数据,代码中采用字符串进行接收,所以最简单的先考虑格式错误。排除格式错误后,重点就来到起始位的检测、奇偶位判断是否匹配和结束符的查找几个方面。最后将相应的结果输出。总的来说难度底,很容易完成。代码及其注释如下:
代码及注释:
package 博客1; import java.util.Scanner; public class 数据流 { public static void main(String[] args) { Scanner sc = new Scanner(System.in); char [] array = new char[10];//用于存放检测到起始位后的十位数据流字符串 String S = sc.nextLine(); int judge = 0;//判断输入字符串是否为无用二进制数据流 for (int mark = 0 ; mark < S.length() ; mark ++){ if(S.charAt(mark)=='0'){//若不是全为1的情况,则将judge置为1 judge = 1; break; } } if(S.length() < 11 || judge == 0){//不足11位为或没有起始位 System.out.println("null data"); } else {//正式开始辣 int num = 1; int mark;//用于奇偶位判断 for(int z = 1 ; z < S.length() ; z++){ mark = 0; if(S.charAt(z-1)=='0'){//检测到起始位 //System.out.println(z); for (int i = 0 ; i < 10 ; i++) {//将起始位后的十个字符存到数组中便于后续比较和使用 array[i] = S.charAt(z+i); if (i<8&&S.charAt(z+i)=='1') {//当在有效部分检测到‘1’时,奇偶记录位加一 mark++; } } if (array[9]!='1') {//当检测到结束符不为1时,输出相应结果 System.out.print(num+":"); num++; System.out.println("validate error"); } else if ( ( (mark%2)==0 && array[8] == '0' ) || ( (mark%2) !=0 && array[8] == '1' ) ) { //当检测到奇偶位和数据奇偶位数不相匹配时,输出相应结果(有奇数个1则奇偶为应该为0,反之为1) System.out.print(num+":"); num++; System.out.println("parity check error"); } else {//当数据格式正确时,输出所有数据 System.out.print(num+":"); num++; for (int m = 0 ; m < 8 ; m++) { if(m!=7) System.out.print(array[m]); else System.out.println(array[m]); }//for:正确数据输出循环 }//else:数据格式无误时的处理 z = z + 10;//处理结束后需要相应跳过已被处理的数据 }//if:检测到起始位后的数据处理 if(S.length()-z<10)//当剩余的字符数量不足以构成一个合法的能够检测的字符串时,结束此次循环 break; }//for:输入数据的循环处理 }//else:输入合适无误后开始的数据检测 }//main }//数据流
类图及复杂度:
类图的话因为并没有说创建多个类,就只有一个,and复杂度如下:
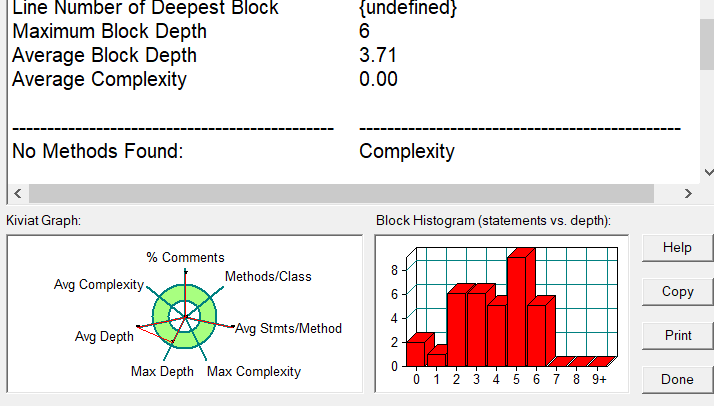
就还蛮......一言难尽的,竟然只有一项在推荐范围内= =但总的来说是一道非常简单的题目
2.计算两点之间的距离
题目要求:
输入两个点的坐标,计算两点之间的距离。输入4个double类型的实数,两个点的x,y坐标,依次是x1、y1、x2、y2,两个点的坐标之间以空格分隔,每个点的x,y坐标以英文“,”分隔。
题目分析:
这道题问题并不难,难就难在输入的处理上,四个坐标要分别用空格个","分隔,所以我们只能是使用字符串格式接收,再将其划分成我们所需要的数据。其中我们需要运用到正则表达式进行比较(我比较蠢没有用,排除了一堆格式错误后还是有问题= =最后把正则表达式当补丁打上去了),将比较过后的字符传化为相应小数,接下来的求解就非常容易了。为了方便操作,定义了一个类“Dian”,方便数据处理以及后续题目应用。
代码及注释:
package 博客1; import java.util.Scanner; public class 点 { public static void main(String[] args) { int judge = 1;//用于判断错误输入 int d = 0;//用于判断不带逗号作为坐标区分的输入 int k = 0;//用于判断不带空格作为点区分的输入 String input;//接收输入字符串 double output;//定义输出 Scanner sc = new Scanner(System.in); input = sc.nextLine();//接收字符串 for (int z = 0; z < input.length() - 1; z++) {//判断字符串输入的格式是否合法 if (input.charAt(z) == ',')//当有逗号作为坐标分隔时,排除一种错误输入格式 d++; if (input.charAt(z) == ' ')//当有空格作为点分隔时,排除一种错误输入格式 k++; if ((input.charAt(z) == ' ' || input.charAt(z) == ',') && (input.charAt(z + 1) == ' ' || input.charAt(z + 1) == ',' || input.charAt(z + 1) == '.')) { //情况1:存在多个符号错误相连 judge = 0; //System.out.println("1"); break; }//+2,-2.3 0.9,-3.2 if ((input.charAt(z) == '.') && (input.charAt(z + 1) < '0' || input.charAt(z + 1) > '9')) { //情况2:符号'.'后不是数字符号 //System.out.println("2"); judge = 0; break; } if ((input.charAt(z) == '+' || input.charAt(z) == '-') && (input.charAt(z + 1) < '0' || input.charAt(z + 1) > '9')) { //情况3:符号’+‘和’-’后不是数字符号 // System.out.println("3"); judge = 0; break; } if ((input.charAt(z) != ' ' && input.charAt(z) != ',' && input.charAt(z) != '.' && input.charAt(z) != '+' && input.charAt(z) != '-') && (input.charAt(z) < '0' || input.charAt(z) > '9')) { //情况4:含义非法字符输入如:abc%¥ // System.out.println("4"); judge = 0; break; } if (z == 0 && (input.charAt(z) == ',' || input.charAt(z) == ' ' || input.charAt(z) == '.')) { //情况5:以合法字符作为开头的错误输入 judge = 0; break; } if (input.charAt(z) == ' ') { int dq = 0; for (int y = 0; y < z; y++) { if (input.charAt(y) == ',') dq = 1; } if (dq == 0) { judge = 0; break; } }//当出现空格时,前方的字符不存在由‘,’分隔的情况的错误输入 } for (int m = 0; m < input.length() - 2; m++) { if (input.charAt(m) == '.' && input.charAt(m + 1) == '0' && (input.charAt(m + 2) == ' ' || input.charAt(m + 2) == ',')) {//情况6:整数采用小数形式输入:x.0 judge = 0; break; } } if (judge == 0 || d == 0 || (d != 1 && k == 0)) {//输入格式错误时,给出相应输出 System.out.println("Wrong Format"); } else { String[] main = input.split(" ");//将合法字符串按照空格分成点坐标字符串:xxx,xx if (main.length != 2) {//如果点字符串不是两个,则为输入的点数量不对 System.out.println("wrong number of points");//给出相应输出 } else { Dian a = new Dian();//定义一个Dian类型的对象 Dian b = new Dian();//定义一个Dian类型的对象 String[] zmy = main[0].split(",");//将坐标字符串按照‘,’分成横坐标和纵坐标 String[] zsh = main[1].split(","); //字符串均合法时 if (!zmy[0].matches("^[-+]?(0|(0\\.\\d+)?|[1-9]\\d*(\\.\\d+)?)$") || !zmy[1].matches("^[-+]?(0|(0\\.\\d+)?|[1-9]\\d*(\\.\\d+)?)$") || !zsh[0].matches("^[-+]?(0|(0\\.\\d+)?|[1-9]\\d*(\\.\\d+)?)$") || !zsh[1].matches("^[-+]?(0|(0\\.\\d+)?|[1-9]\\d*(\\.\\d+)?)$")) { System.out.println("Wrong Format");//匹配相应的格式 } else { a.x = Double.parseDouble(zmy[0]);//赋值给两个点 a.y = Double.parseDouble(zmy[1]); b.x = Double.parseDouble(zsh[0]); b.y = Double.parseDouble(zsh[1]); if (a.y == b.y && a.x == b.x) { System.out.println("Wrong Format"); }//当两个点是同一个点时,算作错误输入(我不理解但是尊重祝福) else { output = b.count(a);//调用距离计算方法并返回相应的结果 System.out.println(output);//输出结果 } } } } } } class Dian{ double x,y; public double count(Dian a){//求两点之间距离 double fin; fin = Math.sqrt(Math.pow((a.x-this.x),2)+Math.pow( (a.y-this.y),2) ); return fin; } boolean collide( Dian b) {//求重合点 if (this.x == b.x && this.y == b.y) return true; else return false; } }
类图及其复杂度:
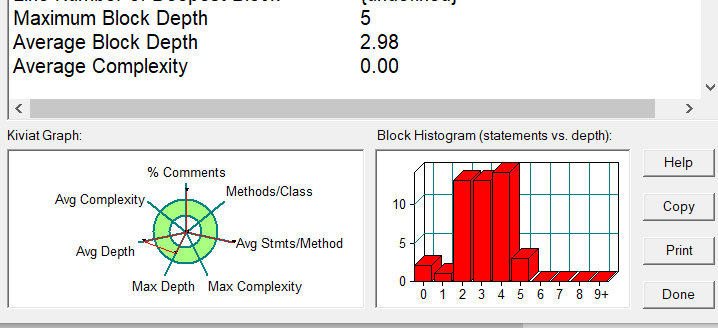
我怎么觉得有亿点点似曾相识??从图中可以看出来其实代码并不是特别好= =只能说功能实现没问题。不算难,只要会正则表达式的运用就好了。
3.线的计算
题目要求:
用户输入一组选项和数据,进行与直线有关的计算。选项包括:
1:输入两点坐标,计算斜率,若线条垂直于X轴,输出"Slope does not exist"。
2:输入三个点坐标,输出第一个点与另外两点连线的垂直距离。
3:输入三个点坐标,判断三个点是否在一条线上,输出true或者false。
4:输入四个点坐标,判断前两个点所构成的直线与后两点构成的直线是否平行,输出true或者false.
5:输入四个点坐标,计算输出前两个点所构成的直线与后两点构成的直线的交点坐标,x、y坐标之间以英文分隔",",并输出交叉点是否在两条线段之内(不含四个端点)的判断结果(true/false),判断结果与坐标之间以一个英文空格分隔。若两条线平行,没有交叉点,则输出"is parallel lines,have no intersection point"。
基本格式:选项+":"+坐标x+","+坐标y+" "+坐标x+","+坐标y。
题目分析
老规矩拿到题目,先看格式,格式方面相较上一题无非就多了一个选项和":",检测起来问题不大。不过题目要求比起上一题就多了很多内容了。首先判断重合,排除后就可以根据具体问题来分析了。写起来不算很难,但是有很多奇奇怪怪的没想到的方面,给编程设计增加了不少难度,逐一补全才能拿到满分(x)完美实现代码功能(√)
代码及注释:
package 博客1; import java.util.Scanner; public class 线 { public static void main(String[] args) { Scanner sc = new Scanner(System.in); int judge = 1,judge2 = 1;//初始化错误输入判断数 String zz = "^[+-]?(0|(0\\.\\d+)?|[1-9]\\d*(\\.\\d+)?)$";//正则表达式 Xian x = new Xian();//new一个线对象 Xian x1 = new Xian();//再new一个线对象,用于选项4,5的两条线的情况 String input = sc.nextLine();//接收输入 if((input.charAt(0)!='1'&&input.charAt(0)!='2'&&input.charAt(0)!='3'&&input.charAt(0)!='4'&&input.charAt(0)!='5')||input.charAt(1)!=':'||(input.charAt(input.length()-1)<'0'||input.charAt(input.length()-1)>'9')) judge = 0;//当开头不满足“(1~5):”格式时,给判断数置0 String text = input.substring(2);//去除开头 // System.out.println(text); String[] zmy = text.split(" ");//按照空格分割字符串 for (int z = 0; z < zmy.length; z++) { String[] zsh = zmy[z].split(",");//按照,分割字符串 if (zsh.length!=2){ judge2 = 0; break; } if (!zsh[0].matches(zz) || !zsh[1].matches(zz)) {//当子字符串格式不匹配时,判断数置0 judge2 = 0; break; } Dian d = new Dian(); x.zmy[z] = d; x1.zmy[z] = d; x.zmy[z].x = Double.parseDouble(zsh[0]);//将x坐标字符转化为数字赋给x点数字第一项。 x.zmy[z].y = Double.parseDouble(zsh[1]);//将y坐标字符转化为数字赋给x点数组第一项。 x1.zmy[z].x = Double.parseDouble(zsh[0]);//将x坐标字符转化为数字赋给x1点数组第一项。 x1.zmy[z].y = Double.parseDouble(zsh[1]);//将y坐标字符转化为数字赋给x1点数组第一项。 } if (judge == 0) {//错误输入1 System.out.println("Wrong Format"); } else if (judge2 == 0) {//错误输入二 System.out.println("Wrong Format"); } else if ((input.charAt(0)=='1'&&zmy.length!=2)||((input.charAt(0)=='2'||input.charAt(0)=='3')&&zmy.length!=3)||((input.charAt(0)=='4'||input.charAt(0)=='5')&&zmy.length!=4)){//选项位与输入点个数不匹配 System.out.println("wrong number of points"); } else { if (input.charAt(0) == '1') {//选项1 if (x.zmy[0].x == x.zmy[1].x && x.zmy[0].y != x.zmy[1].y)//判断斜率 System.out.println("Slope does not exist"); else if (x.collide(x.zmy[0], x.zmy[1])) {//判断重合点 System.out.println("points coincide"); } else {//计算斜率 System.out.println(x.slope(x.zmy[0], x.zmy[1])); } } else if (input.charAt(0) == '2') {//选项2 if (x.collide(x.zmy[0], x.zmy[1]) || x.collide(x.zmy[0], x.zmy[2]) || x.collide(x.zmy[2], x.zmy[1])) System.out.println("points coincide"); else { double output; x.A = x.zmy[2].y - x.zmy[1].y; x.B = x.zmy[1].x - x.zmy[2].x; x.C = x.zmy[2].x * x.zmy[1].y - x.zmy[1].x * x.zmy[2].y; //实际上后面优化了次部分,可直接使用方法计算abc output = (x.A * x.zmy[0].x + x.B * x.zmy[0].y + x.C) / Math.sqrt(Math.pow(x.A, 2) + Math.pow(x.B, 2)); if (output < 0)//取绝对值 output = -output; System.out.println(output); } } else if (input.charAt(0) == '3') {//选项3 if (x.collide(x.zmy[0], x.zmy[1]) || x.collide(x.zmy[0], x.zmy[2]) || x.collide(x.zmy[2], x.zmy[1])) System.out.println("points coincide"); else {//计算前两点直线公式,带入第三个点 x.A = x.zmy[2].y - x.zmy[1].y; x.B = x.zmy[1].x - x.zmy[2].x; x.C = x.zmy[2].x * x.zmy[1].y - x.zmy[1].x * x.zmy[2].y; if (x.A * x.zmy[0].x + x.B * x.zmy[0].y + x.C == 0) System.out.println("true"); else System.out.println("false"); } } else if (input.charAt(0) == '4') {//选项四 if (x.collide(x.zmy[0], x.zmy[1])|| x.collide(x.zmy[2], x.zmy[3])) System.out.println("points coincide"); else { if (x.parallel(x, x1))//判断平行 System.out.println("true"); else System.out.println("false"); } } else {//选项5 if (x.collide(x.zmy[0], x.zmy[1]) || x.collide(x.zmy[2], x.zmy[3])) System.out.println("points coincide"); else { if (x.parallel(x, x1))//判断平行 System.out.println("is parallel lines,have no intersection point"); else { double outX, outY; double bx, sx, by, sy; double bx1, sx1, by1, sy1; //取两条直线四个端点的大小顺序 sx = Math.min(x.zmy[0].x,x.zmy[1].x); bx = Math.max(x.zmy[0].x,x.zmy[1].x); sx1 = Math.min(x1.zmy[2].x,x1.zmy[3].x); bx1 = Math.max(x1.zmy[2].x,x1.zmy[3].x); sy = Math.min(x.zmy[0].y,x.zmy[1].y); by = Math.max(x.zmy[0].y,x.zmy[1].y); sy1 = Math.min(x1.zmy[2].y,x1.zmy[3].y); by1 = Math.max(x1.zmy[2].y,x1.zmy[3].y); String outS="";//初始化输出字符 //y = ( c1 * a2 - c2 * a1) / ( a1 * b2 - a2 * b1) //x = ( c2 * b1 - c1 * b2) / ( a1 * b2 - a2 * b1) x.abcCount(x.zmy[0],x.zmy[1]); x1.abcCount(x1.zmy[2],x1.zmy[3]); outX = (x1.C * x.B - x.C * x1.B) / (x.A * x1.B - x1.A * x.B);//计算交点 outY = (x.C * x1.A - x1.C * x.A) / (x.A * x1.B - x1.A * x.B); if(x.A==0||x.B==0){//当出现坐标轴平行直线时 if(x.A==0){//与x轴平行 if(outX<sx||outX>bx)//只需要比较x且不能相等 outS = "false"; else outS = "true"; } else if(x.B==0)//与y轴平行 { if (outY<sy||outY>by)//只比较y且不能相等 outS = "false"; else outS = "true"; } } if(x1.A==0||x1.B==0){ if (x1.A==0){ if(outX<sx1||outX>bx1) outS = "false"; else outS = "true"; } else if(x1.B==0) { if (outY<sy1||outY>by1) outS = "false"; else outS = "true"; } } if(x.A!=0&&x.B!=0&&x1.A!=0&&x1.B!=0) {//当两条直线均不和坐标轴平行时,比较其交点坐标的x值与y值和两条线段的端点的大小,判断是否在线上 if (((outX > sx && outX < bx) || (outY > sy && outY < by)) || ((outX > sx1 && outX < bx1) || (outY > sy1 && outY < by1))) outS = "true"; else outS = "false"; } System.out.println(outX + "," + outY + " " + outS); } } } } } } //5:1,3 -2,3 -2,+5 1,3 class Dian{ double x,y; public double count(Dian a){//求两点之间距离 double fin; fin = Math.sqrt(Math.pow((a.x-this.x),2)+Math.pow( (a.y-this.y),2) ); return fin; } boolean collide( Dian b) {//求重合点 if (this.x == b.x && this.y == b.y) return true; else return false; } } class Xian{ Dian [] zmy = new Dian[99]; double A,B,C; boolean collide(Dian a,Dian b){//判断重合 if (a.x == b.x&&a.y==b.y) return true; else return false; } double slope(Dian a,Dian b){//求斜率 double sSlope; if(a.x==b.x) sSlope = 100000000; else sSlope = (b.y - a.y)/(b.x - a.x); return sSlope; } void abcCount(Dian a,Dian b){//计算直线一般式ABC this.A = b.y - a.y; this.B = a.x - b.x; this.C = b.x * a.y - b.y * a.x; } boolean parallel(Xian x1 , Xian x2){//平行线判断 double slope1,slope2; slope1 = x1.slope(x1.zmy[0],x1.zmy[1]); slope2 = x1.slope(x2.zmy[2],x2.zmy[3] ); x1.C = x1.zmy[1].x * x1.zmy[0].y - x1.zmy[0].x * x1.zmy[1].y; x2.C = x2.zmy[3].x * x2.zmy[2].y - x2.zmy[2].x * x2.zmy[3].y; if (slope1==slope2) return true; else return false; } double lengthCount(Dian a){//求点a到此直线的距离 double length; length = Math.abs(this.A*a.x+this.B*a.y+this.C)/Math.sqrt(Math.pow(this.A,2)+Math.pow(this.B,2)); return length; } }
类图及复杂度:

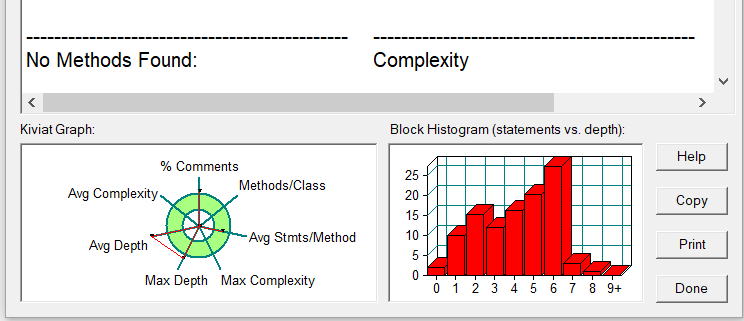
总结一下代码就只是能跑的程度(只要人和代码有一个能跑就......)
4.三角形的计算
题目要求:
用户输入一组选项和数据,进行与三角形有关的计算。选项包括:
1:输入三个点坐标,判断是否是等腰三角形、等边三角形,判断结果输出true/false,两个结果之间以一个英文空格符分隔。
2:输入三个点坐标,输出周长、面积、重心坐标,三个参数之间以一个英文空格分隔,坐标之间以英文","分隔。
3:输入三个点坐标,输出是钝角、直角还是锐角三角形,依次输出三个判断结果(true/false),以一个英文空格分隔,
4:输入五个点坐标,输出前两个点所在的直线与三个点所构成的三角形相交的交点数量,如果交点有两个,则按面积大小依次输出三角形被直线分割成两部分的面积。若直线与三角形一条线重合,输出"The point is on the edge of the triangle"
5:输入四个点坐标,输出第一个是否在后三个点所构成的三角形的内部(输出in the triangle/outof triangle)。
必须使用射线法,原理:由第一个点往任一方向做一射线,射线与三角形的边的交点(不含点本身)数量如果为1,则在三角形内部。如果交点有两个或0个,则在三角形之外。若点在三角形的某条边上,输出"on the triangle"
基本格式:选项+":"+坐标x+","+坐标y+" "+坐标x+","+坐标y。点的x、y坐标之间以英文","分隔,点与点之间以一个英文空格分隔。
题目分析:
输入格式和上一题没什么区别,无非就是点的数量不一样,数据处理也一样使用正则表达式和相应的字符串-浮点数转化,得到数据后我们来开始具体分析问题。首先,三点无法构成三角形的条件是:三点不共线(有笨蛋还考虑三条线段长度的吗?是的就是我,被自己蠢哭)。我们在三角形类里定义一个方法用作排除掉无法构成三角形的情况,在数据处理开始时使用。接下来的就都很“简单”了,无非就是根据题目,相处相应的数据处理办法,具体情况包含在代码注释中。
代码及其注释:
package 博客1; import java.math.BigDecimal; import java.util.Scanner; public class 三角形 { public static void main(String[] args) { Scanner sc = new Scanner(System.in); triangle tria = new triangle();//new一个三角形 Dian [] points = new Dian[999]; int judge = 1,judge2 = 1;//初始化错误输入判断数 String zz = "^[+-]?(0|(0\\.\\d+)?|[1-9]\\d*(\\.\\d+)?)$";//正则表达式 String input = sc.nextLine();//接收输入 if((input.charAt(0)!='1'&&input.charAt(0)!='2'&&input.charAt(0)!='3'&&input.charAt(0)!='4'&&input.charAt(0)!='5')||input.charAt(1)!=':'||(input.charAt(input.length()-1)<'0'||input.charAt(input.length()-1)>'9')) judge = 0;//当开头不满足“(1~5):”格式时,给判断数置0 String text = input.substring(2);//去除开头 // System.out.println(text); String[] zmy = text.split(" ");//按照空格分割字符串 for (int z = 0; z < zmy.length; z++) { String[] zsh = zmy[z].split(",");//按照,分割字符串 if (zsh.length!=2){//当坐标格式不为x,x时即有多余成分(such as: ,,)判断数置0 judge2 = 0; break; } if (!zsh[0].matches(zz) || !zsh[1].matches(zz)) {//当子字符串格式不匹配时,判断数置0 //1:,1 3,4 2 judge2 = 0; break; } Dian a = new Dian(); points[z] = a; points[z].x = Double.parseDouble(zsh[0]); points[z].y = Double.parseDouble(zsh[1]); } if (judge == 0) {//错误输入1 System.out.println("Wrong Format"); } else if (judge2 == 0) {//错误输入二 System.out.println("Wrong Format"); } else if ((input.charAt(0)=='1'||input.charAt(0)=='2'||input.charAt(0)=='3')&&zmy.length!=3 || (input.charAt(0)=='4'&&zmy.length!=5)||input.charAt(0)=='5'&&zmy.length!=4){ //选项和输入的点的个数不匹配时 System.out.println("wrong number of points"); } //大的要来辣!!!!!! else {//1:0,0 0,0 4,0 if (input.charAt(0)=='1'){//选项1 tria.A = points[0]; tria.B = points[1]; tria.C = points[2]; if (!tria.triangleJudge(tria.A, tria.B, tria.C))//无法构成三角形 System.out.println("data error"); else { double length1,length2,length3; length1 = tria.A.count(tria.B);//计算AB长度 length2 = tria.A.count(tria.C); length3 = tria.B.count(tria.C); if (length1==length2 || length2==length3 || length1==length3)//等腰 System.out.print("true "); else System.out.print("false "); if (length1==length2 && length1==length3 && length2==length3)//等边 System.out.println("true"); else System.out.println("false"); } } else if (input.charAt(0)=='2'){//选项2 tria.A = points[0]; tria.B = points[1]; tria.C = points[2]; if (!tria.triangleJudge(tria.A, tria.B, tria.C)) System.out.println("data error"); else { double length,area,outX,outY; length = change(tria.A.count(tria.B)+tria.A.count(tria.C)+tria.B.count(tria.C)); //计算周长并将其转化为最多四舍五入保留小数点后六位 Xian x = new Xian(); tria.x1 = x; tria.x1.abcCount(tria.A, tria.B);//计算线AB的一般式系数ABC area = change((tria.x1.lengthCount(tria.C)*tria.A.count(tria.B))/2);//计算面积 outX = change((tria.A.x+tria.B.x+tria.C.x)/3);//计算重心坐标 outY = change((tria.A.y+tria.B.y+tria.C.y)/3); System.out.println(length+" "+area+" "+outX+","+outY); } } else if(input.charAt(0)=='3'){//选项3 tria.A = points[0]; tria.B = points[1]; tria.C = points[2]; if (!tria.triangleJudge(tria.A, tria.B, tria.C)) System.out.println("data error"); else { double x1,x2,x3,m,max,s,min; x1 = tria.A.count(tria.B);//计算线段AB长度 x2 = tria.A.count(tria.C); x3 = tria.B.count(tria.C); m = Math.max(x1,x2); min = Math.min(x1,x2); max =Math.max(m,x3); s = Math.min(m,x3); if (Math.sqrt(s*s+min*min)<max)//两边平方和开方小于第三边,为钝角三角形 System.out.println("true false false"); else if (Math.sqrt(s*s+min*min)-max<=0.0001)//两边平方和开方等于第三边,为直角三角形 System.out.println("false true false"); else if (Math.sqrt(s*s+min*min)>max)//两边平方和开方大于第三边,为锐角三角形 System.out.println("false false true"); } } else if(input.charAt(0)=='4'){//选项四 if (points[0].collide(points[1]))//判断前两个点是否重合 System.out.println("points coincide"); else { tria.A = points[2]; tria.B = points[3]; tria.C = points[4]; if (!tria.triangleJudge(tria.A, tria.B, tria.C)) System.out.println("data error"); else { Xian x = new Xian(); Dian d1 = new Dian(); Dian d2 = new Dian(); x.zmy[0] = d1; x.zmy[0].x = points[0].x; x.zmy[0].y = points[0].y; x.zmy[1] = d2; x.zmy[1].x = points[1].x; x.zmy[1].y = points[1].y; x.abcCount(points[0],points[1] );//计算直线一般式 Xian X1= new Xian();//三角形三条边 Xian X2= new Xian(); Xian X3= new Xian(); tria.x1 = X1; tria.x2 = X2; tria.x3 = X3; tria.x1.zmy[0] = tria.A;//线x1为线AB tria.x1.zmy[1] = tria.B; tria.x2.zmy[0] = tria.A;//线x2为线AC tria.x2.zmy[1] = tria.C; tria.x3.zmy[0] = tria.B;//线x3为线BC tria.x3.zmy[1] = tria.C; tria.x1.abcCount(tria.A, tria.B);//计算一般式 tria.x2.abcCount(tria.A, tria.C); tria.x3.abcCount(tria.B, tria.C); if (((x.A*tria.A.x+ x.B*tria.A.y+ x.C==0)&&(x.A*tria.B.x+ x.B*tria.B.y+ x.C==0))||((x.A*tria.C.x+ x.B*tria.C.y+ x.C==0)&&(x.A*tria.B.x+ x.B*tria.B.y+ x.C==0))||((x.A*tria.A.x+ x.B*tria.A.y+ x.C==0)&&(x.A*tria.C.x+ x.B*tria.C.y+ x.C==0))){ //如果顶点带入直线x方程成立,说明直线和边重合 System.out.println("The point is on the edge of the triangle"); } else {//当x和三条边都没有交点时 if ((!tria.pointJudge1(tria.x1,x))&&(!tria.pointJudge2(tria.x2,x))&&(!tria.pointJudge3(tria.x3,x))){ System.out.println("0");//4:-5,0 -5,-3 0,0 0,2 2,0 //4:-3,0 0,-3 -2,0 0,2 2,0 }//当只有一个交点时 else if ((x.A * tria.A.x + x.B * tria.A.y + x.C==0&&!tria.pointJudge3(tria.x3,x))||(x.A * tria.B.x + x.B * tria.B.y + x.C==0&&!tria.pointJudge2(tria.x2,x))|| (x.A * tria.C.x + x.B * tria.C.y + x.C==0&&!tria.pointJudge1(tria.x1,x))){ System.out.println("1"); } else {//当有两个交点时 double tArea = Math.sqrt(Math.pow(tria.A.x-tria.B.x,2)+Math.pow(tria.A.y-tria.B.y,2))*tria.x1.lengthCount(tria.C)/2; double area1,area2; double l1,l2,l3; Dian dian1 = new Dian(); Dian dian2 = new Dian(); Dian dian3 = new Dian(); int jJudge = 1; if (x.A * tria.A.x + x.B * tria.A.y + x.C==0){//过A点将三角形分成两个三角形 dian1 = tria.A;//交点1为A点 dian2 = getDian(x, tria.x3);//计算交点2 l1 = Math.sqrt(Math.pow(dian1.x-dian2.x,2)+Math.pow(dian1.y-dian2.y,2));//计算底边长度 l2 = x.lengthCount(tria.B);//计算B到直线x的距离 l3 = x.lengthCount(tria.C);//计算C到直线x的距离 area1 = l1*l2/2; area2 = l1*l3/2; jJudge = 0; if (area2>area1){ System.out.println("2 "+change(area1)+" "+change(area2)); } else System.out.println("2 "+change(area2)+" "+change(area1)); } if (x.A * tria.B.x + x.B * tria.B.y + x.C==0){//过B点将三角形分成两个三角形 dian1 = tria.B; dian2 = getDian(x, tria.x2); l1 = Math.sqrt(Math.pow(dian1.x-dian2.x,2)+Math.pow(dian1.y-dian2.y,2)); l2 = x.lengthCount(tria.C); l3 = x.lengthCount(tria.A); area1 = l1*l2/2; area2 = l1*l3/2; jJudge = 0; if (area2>area1){ System.out.println("2 "+change(area1)+" "+change(area2)); } else System.out.println("2 "+change(area2)+" "+change(area1)); } if (x.A * tria.C.x + x.B * tria.C.y + x.C==0){////过C点将三角形分成两个三角形 dian1 = tria.C; dian2 = getDian(x, tria.x1); l1 = Math.sqrt(Math.pow(dian1.x-dian2.x,2)+Math.pow(dian1.y-dian2.y,2)); l2 = x.lengthCount(tria.B); l3 = x.lengthCount(tria.A); area1 = l1*l2/2; area2 = l1*l3/2; jJudge = 0; if (area2>area1){ System.out.println("2 "+change(area1)+" "+change(area2)); } else System.out.println("2 "+change(area2)+" "+change(area1)); } //当直线x和某条边的交点不在三角形上时,则两个交点和该边相对顶点会构成一个三角形(如直线和边AB的交点不在三角形上,则与边AC、BC相交与点E、F,此时CEF是一个三角形) // 此时则可通过计算该边相对顶点到直线的距离计算出其中一个划分后面积,再拿总面积减去该部分得到剩下的面积,下面的代码就是依此编写的 if (!tria.pointJudge1(tria.x1 ,x)&&jJudge!=0){//直线与x1的交点不在三角形的边上 dian1 = getDian(x, tria.x2); dian2 = getDian(x, tria.x3); l1 = Math.sqrt(Math.pow(dian1.x-dian2.x,2)+Math.pow(dian1.y-dian2.y,2));//计算两个交点的距离 l2 = x.lengthCount(tria.C);//计算顶点C到直线的距离 area1 = l2*l1/2; area2 = tArea - area1; if (area2>area1){ System.out.println("2 "+change(area1)+" "+change(area2)); } else System.out.println("2 "+change(area2)+" "+change(area1)); } if (!tria.pointJudge2(tria.x2, x)&&jJudge!=0){ dian1 = getDian(x, tria.x1); dian2 = getDian(x, tria.x3); l1 = Math.sqrt(Math.pow(dian1.x-dian2.x,2)+Math.pow(dian1.y-dian2.y,2)); l2 = x.lengthCount(tria.B); area1 = l2*l1/2; area2 = tArea - area1; if (area2>area1){ System.out.println("2 "+change(area1)+" "+change(area2)); } else System.out.println("2 "+change(area2)+" "+change(area1)); } if (!tria.pointJudge3(tria.x3, x)&&jJudge!=0){ dian1 = getDian(x, tria.x2); dian2 = getDian(x, tria.x1); l1 = Math.sqrt(Math.pow(dian1.x-dian2.x,2)+Math.pow(dian1.y-dian2.y,2)); l2 = x.lengthCount(tria.A); area1 = l2*l1/2; area2 = tArea - area1; if (area2>area1){ System.out.println("2 "+change(area1)+" "+change(area2)); } else System.out.println("2 "+change(area2)+" "+change(area1)); } } } } } } else {//选项5 tria.A = points[1]; tria.B = points[2]; tria.C = points[3]; if (!tria.triangleJudge(tria.A, tria.B, tria.C)) System.out.println("data error"); else { Xian X1= new Xian(); Xian X2= new Xian(); Xian X3= new Xian(); tria.x1 = X1;//定义三角形三条边 tria.x2 = X2; tria.x3 = X3; tria.x1.zmy[0] = tria.A; tria.x1.zmy[1] = tria.B; tria.x2.zmy[0] = tria.A; tria.x2.zmy[1] = tria.C; tria.x3.zmy[0] = tria.B; tria.x3.zmy[1] = tria.C; tria.x1.abcCount(tria.A, tria.B);//计算三条边一般式 tria.x2.abcCount(tria.A, tria.C); tria.x3.abcCount(tria.B, tria.C); Dian d = new Dian(); d.x = points[0].x; d.y = points[0].y; double tArea = Math.sqrt(Math.pow(tria.A.x-tria.B.x,2)+Math.pow(tria.A.y-tria.B.y,2))*tria.x1.lengthCount(tria.C)/2; //计算总面积 if (tria.x1.A * d.x + tria.x1.B * d.y + tria.x1.C==0||tria.x2.A*d.x+tria.x2.B*d.y+tria.x2.C==0||tria.x3.A*d.x+tria.x3.B*d.y+tria.x3.C==0) System.out.println("on the triangle");//点在任意一条边上时 else { double l1,l2,l3; double x1,x2,x3; l1 = tria.x1.lengthCount(d);//计算三条边的长度 l2 = tria.x2.lengthCount(d); l3 = tria.x3.lengthCount(d); x1 = Math.sqrt(Math.pow(tria.A.x-tria.B.x,2)+Math.pow(tria.A.y-tria.B.y,2));//计算点和任意两顶点构成三角形的面积 x2 = Math.sqrt(Math.pow(tria.A.x-tria.C.x,2)+Math.pow(tria.A.y-tria.C.y,2)); x3 = Math.sqrt(Math.pow(tria.C.x-tria.B.x,2)+Math.pow(tria.C.y-tria.B.y,2)); if (Math.sqrt((l1*x1+l2*x2+l3*x3)/2-tArea)<0.0001)//当三个面积相加刚好等于三角形面积时。则点在三角形内 System.out.println("in the triangle"); else System.out.println("outof the triangle"); } } } } } public static double change(double d){//转化为六位小数 double d1; BigDecimal big = new BigDecimal(d); d1 = big.setScale(6,BigDecimal.ROUND_HALF_UP).doubleValue(); return d1; } public static boolean match(Xian x , Xian y ,Xian z){//比较斜率 double slope1,slope2,slope3; if (x.zmy[1].x-x.zmy[0].x==0)//斜率不存在时,将其记为一个很大的值,用于比较 slope1 = 10000000000.0; else { slope1 = (x.zmy[1].y - x.zmy[0].y) / (x.zmy[1].x - x.zmy[0].x); } if (y.zmy[1].x-y.zmy[0].x==0) slope2 = 10000000000.0; else { slope2 = (y.zmy[1].y - y.zmy[0].y) / (y.zmy[1].x - y.zmy[0].x); } if (z.zmy[1].x-z.zmy[0].x==0) slope3 = 10000000000.0; else { slope3 = (z.zmy[1].y - z.zmy[0].y) / (z.zmy[1].x - z.zmy[0].x); } //4:0,-3 4,0 0,0 0,4 4,0 if (slope1>Math.min(slope2,slope3)&&slope1<Math.max(slope2,slope3))//如果目标直线斜率在经过点的两条边的斜率之间,则有一个交点 return true; else return false; } public static Dian getDian(Xian x,Xian y){//计算交点 Dian re = new Dian(); re.x = (y.C * x.B - x.C * y.B) / (x.A * y.B - y.A * x.B); re.y = (x.C * y.A - y.C * x.A) / (x.A * y.B - y.A * x.B); return re; } } //5:1,3 -2,3 -2,+5 1,3 class Dian{ double x,y; public double count(Dian a){//求两点之间距离 double fin; fin = Math.sqrt(Math.pow((a.x-this.x),2)+Math.pow( (a.y-this.y),2) ); return fin; } boolean collide( Dian b) {//求重合点 if (this.x == b.x && this.y == b.y) return true; else return false; } } class Xian{ Dian [] zmy = new Dian[2]; double A,B,C; boolean collide(Dian a,Dian b){//判断重合 if (a.x == b.x&&a.y==b.y) return true; else return false; } double slope(Dian a,Dian b){//求斜率 double sSlope; sSlope = (b.y - a.y)/(b.x - a.x); return sSlope; } void abcCount(Dian a,Dian b){//计算直线一般式ABC this.A = b.y - a.y; this.B = a.x - b.x; this.C = b.x * a.y - b.y * a.x; } boolean parallel(Xian x1 , Xian x2){//平行线判断 double slope1,slope2; slope1 = x1.slope(x1.zmy[0],x1.zmy[1]); slope2 = x1.slope(x2.zmy[2],x2.zmy[3] ); if (slope1==slope2)//斜率相等 return true; else return false; } double lengthCount(Dian a){//求点a到此直线的距离 double length; length = Math.abs(this.A*a.x+this.B*a.y+this.C)/Math.sqrt(Math.pow(this.A,2)+Math.pow(this.B,2)); return length; } } class triangle { Dian A, B, C; Xian x1, x2, x3; //x1:AB ;x2:AC ;x3:BC boolean triangleJudge(Dian A, Dian B, Dian C) {//判断三角形是否合法 int judge = 1; Xian x1 = new Xian(); x1.A = B.y - A.y; x1.B = A.x - B.x; x1.C = B.x * A.y - B.y * A.x; if (x1.A * C.x + x1.B * C.y + x1.C == 0)//三点共线时不能构成三角形 judge = 0; if (judge == 1)//如果是合法三角形 return true; else return false; } boolean collide(Dian a, Dian b) {//求重合点 if (a.x == b.x && a.y == b.y) return true; else return false; } boolean pointJudge1(Xian x1,Xian x){//判断直线与x1的交点是否在三角形内 double outX,outY; double slope1 = (this.A.y - this.B.y)/(this.A.x-this.B.x);//求x1的斜率 double slope2 = (x.zmy[1].y-x.zmy[0].y)/(x.zmy[1].x-x.zmy[0].x);//求输入线的斜率 if (slope1==slope2) {//当平行时,没有交点 return false; } else{ outX = (x1.C * x.B - x.C * x1.B) / (x.A * x1.B - x1.A * x.B);//计算交点 outY = (x.C * x1.A - x1.C * x.A) / (x.A * x1.B - x1.A * x.B); if (x1.A==0){//与X轴平行 if ((outX >= Math.min(this.A.x,this.B.x) && outX <= Math.max(this.A.x,this.B.x)) || (outY > Math.min(this.A.y,this.B.y) && outY < Math.max(this.A.y,this.B.y))){ return true; } else return false; } if (x1.B==0) {//与Y轴平行 if ((outX > Math.min(this.A.x, this.B.x) && outX < Math.max(this.A.x, this.B.x)) || (outY >= Math.min(this.A.y, this.B.y) && outY <= Math.max(this.A.y, this.B.y))) { return true; } else return false; } else {//当交点在AB之间时(x和y任意一项在AB两点之间) if ((outX >= Math.min(this.A.x, this.B.x) && outX <= Math.max(this.A.x, this.B.x)) || (outY >= Math.min(this.A.y, this.B.y) && outY <= Math.max(this.A.y, this.B.y))) { return true; } else { return false; } } } } boolean pointJudge2(Xian x2,Xian x){//判断直线与x2的交点是否在三角形内 double outX,outY; double slope1 = (this.A.y - this.C.y)/(this.A.x-this.C.x);//0 double slope2 = (x.zmy[1].y-x.zmy[0].y)/(x.zmy[1].x-x.zmy[0].x);//-2v if (slope1==slope2) { // System.out.println("ffffff2-1"); return false; } else{ outX = (x2.C * x.B - x.C * x2.B) / (x.A * x2.B - x2.A * x.B);//1 outY = (x.C * x2.A - x2.C * x.A) / (x.A * x2.B - x2.A * x.B);//0 // System.out.println(this.A.x+" "+this.C.x+" ||||||| "+this.A.y+" "+this.C.y); // System.out.println(outX+" "+outY); if (x2.A==0){ //0 //4 if ((outX >= Math.min(this.A.x,this.C.x) && outX <= Math.max(this.A.x,this.C.x)) || (outY > Math.min(this.A.y,this.C.y) && outY < Math.max(this.A.y,this.C.y))){ return true; } else return false; } if (x2.B==0) { if ((outX > Math.min(this.A.x, this.C.x) && outX < Math.max(this.A.x, this.C.x)) || (outY >= Math.min(this.A.y, this.C.y) && outY <= Math.max(this.A.y, this.C.y))) { return true; } else return false; } else { if ((outX >= Math.min(this.A.x, this.C.x) && outX <= Math.max(this.A.x, this.C.x)) || (outY >= Math.min(this.A.y, this.C.y) && outY <= Math.max(this.A.y, this.C.y))) { return true; } else { // System.out.println("fffff2-2"); return false; } } } } boolean pointJudge3(Xian x3,Xian x){//判断直线与x2的交点是否在三角形内 double outX,outY; double slope1 = (this.C.y - this.B.y)/(this.C.x-this.B.x); double slope2 = (x.zmy[1].y-x.zmy[0].y)/(x.zmy[1].x-x.zmy[0].x); if (slope1==slope2) { // System.out.println("ffffff3-1"); return false; } else{ outX = (x3.C * x.B - x.C * x3.B) / (x.A * x3.B - x3.A * x.B); outY = (x.C * x3.A - x3.C * x.A) / (x.A * x3.B - x3.A * x.B); // System.out.println(this.C.x+" "+this.B.x+" ||||||| "+this.C.y+" "+this.B.y); // System.out.println(outX+" "+outY); if (x3.A==0){ if ((outX >= Math.min(this.C.x,this.B.x) && outX <= Math.max(this.C.x,this.B.x)) || (outY > Math.min(this.C.y,this.B.y) && outY < Math.max(this.C.y,this.B.y))){ return true; } else return false; } if (x3.B==0) { if ((outX > Math.min(this.C.x, this.B.x) && outX < Math.max(this.C.x, this.B.x)) || (outY >= Math.min(this.C.y, this.B.y) && outY <= Math.max(this.C.y, this.B.y))) { return true; } else return false; } else { if ((outX >= Math.min(this.C.x, this.B.x) && outX <= Math.max(this.C.x, this.B.x)) || (outY >= Math.min(this.C.y, this.B.y) && outY < Math.max(this.C.y, this.B.y))) { return true; } else { // System.out.println("ffffff3-2"); return false; } } } } }
类图及复杂度:
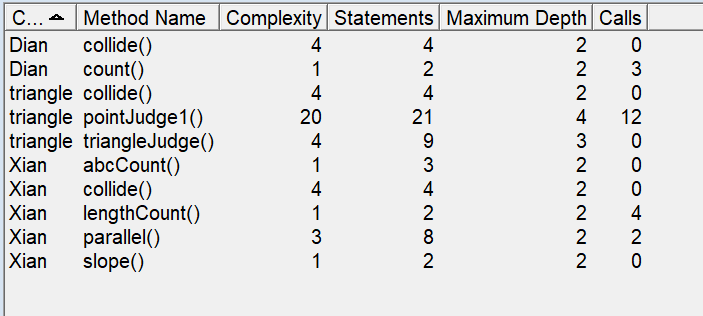
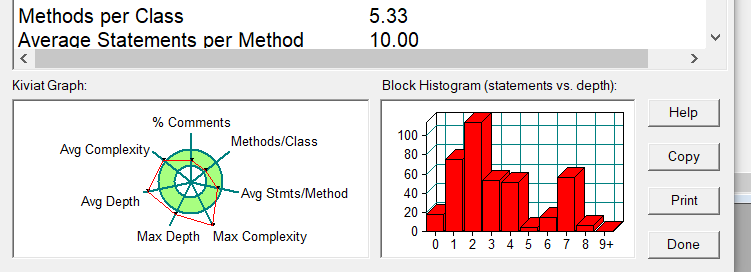
可以看到其中某些方法的复杂度过高(说的就是你 pointJudge1),总的来说比前几个代码稍微好一点。
BUG及编写问题集合
接下来说几个编程过程中遇到的折磨得我食不下咽(bushi)的bug和问题
1.空指针异常
最经典的错误,后面三道题都报过这种错,归根到底就是——没有new对象就直接使用了导致空指针异常,代码中(特别是三角形那题)涉及到很多对象的创建所以真的是老是报这个错误。
2.数组越界
这个倒是很容易解决,只要把数组大小设置合适就好了,但是也是很容易没注意到的错误。
3.计算斜率的时候没有考虑斜率不存在情况。代码运行后普通的输入进行检测也没检测出来,后来突发奇想才想到这个问题。解决办法选择了当斜率不存在时将斜率置成一个很大的数(1000000)
4.第三次作业的7-3有一个问题:当计算线段和边的交点是不是在三角形上时,忘记了判断线段的端点刚好为交点的情况,修改后在判断条件上增加了等于。但是加了等号后又出现了另一个问题:当斜率为0或者斜率不存在时,等号又不能成立,所以又增加了这两种特殊情况的计算。
总结
总的来说这三次作业并没有太难,虽然相较于第一二次作业,第三次作业的难度提升较大,但是其实只有仔细分析好问题,再结合学习的代码知识,想要编写一个大概的能运行能执行基本操作的程序不算太难。在此基础上慢慢细化一些细节部分,将代码功能补全,这个过程就需要我们发散思维,对可能出现的情况和问题在代码中给出相应的解决方案。最基本的比如说输入格式错误啊,除法计算时除数为0啊这些说出来都觉得平常但是代码中容易遗漏的东西。除此之外就是题目中隐含的一些要求和特殊情况,需要自己结合题意慢慢分析,再逐步完善。
这里特别要说一下完成第三次作业后我的收获,我可以说深刻地感受到了类的重要性。从题目上看从点到线到三角形(到下次的四边形和五边形),当你处理好每一个类后,会给后面的类和功能代码的编写省去很多的麻烦。在之后的代码编写过程中我也会更加注意类的定义和使用。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号