洛谷 P7372 [COCI2018-2019#4] Slagalica

洛谷传送门

LOJ 传送门

模拟赛赛时被这题题面唬住了，没想到原来这么简单/ll。

设第 \(i\) 个位置经过变化后的位置为 \(p_i\)。那么连边 \(i \to p_i\) 后所有环长的 \(\text{lcm}\) 为 \(K\)。

考虑先构造一组数 \(\{a_n\}\) 使得 \(\text{lcm}(a_1, a_2, \ldots, a_n) = K\) 且 \(\sum\limits_{i = 1}^n a_i\) 最小，\(a_i\) 表示第 \(i\) 个环的环长。结论是把 \(K\) 质因数分解后取 \(a_i = p_i^{e_i}\) 即可。

所以现在我们的任务是构造一些长度给定的环。考虑走 S 形拎出一条链（借用一下 Liquefyx 的图）：

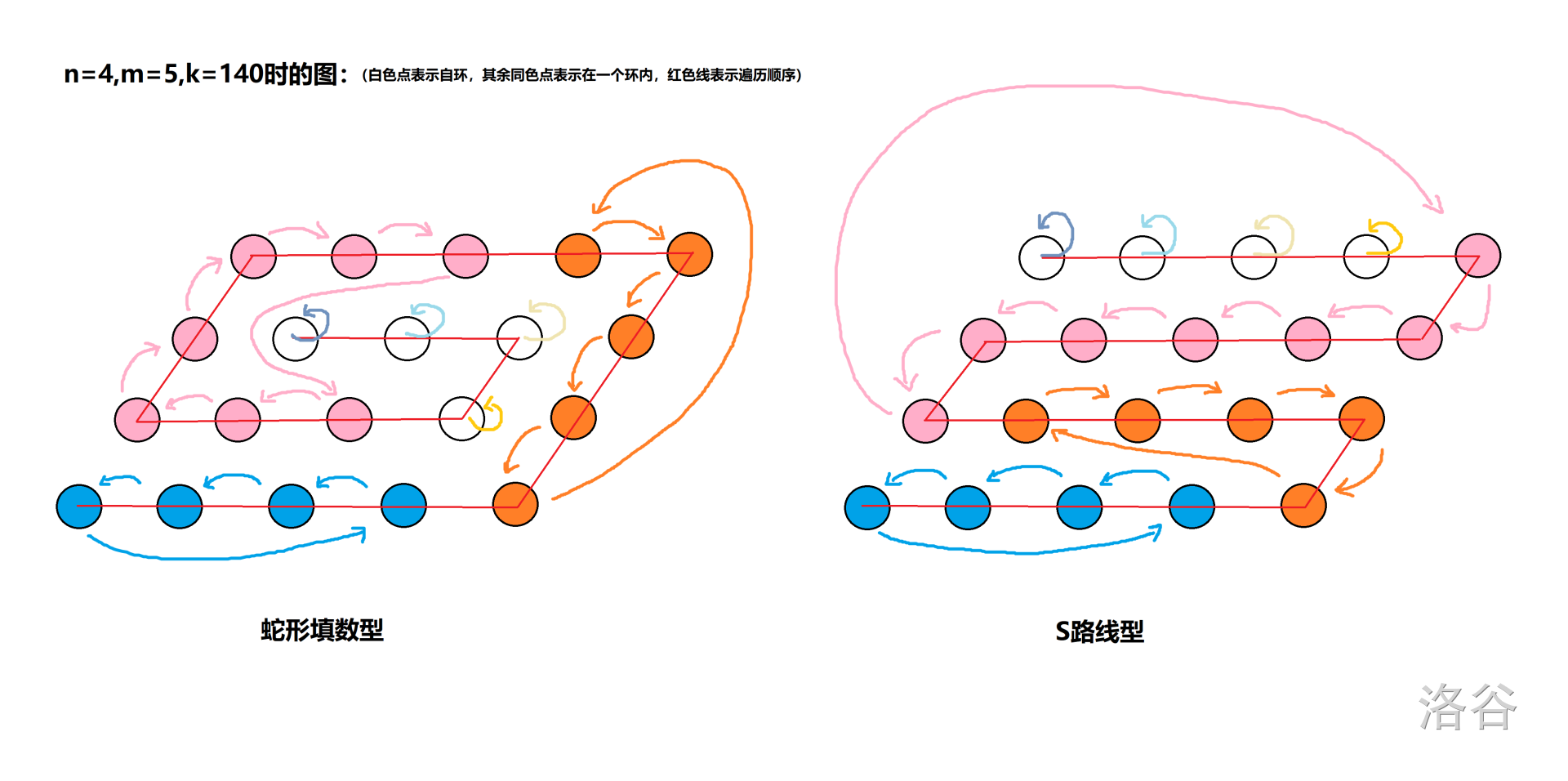
所以我们如果可以交换相邻两个数，那么每次把链的第一个点逐个地交换到末尾即可。

写爆搜或者手玩可以得出交换相邻两个数的方案。于是这题就做完了。

code

#include <bits/stdc++.h>
#define pb emplace_back
#define fst first
#define scd second
#define mkp make_pair
#define mems(a, x) memset((a), (x), sizeof(a))

using namespace std;
typedef long long ll;
typedef double db;
typedef unsigned long long ull;
typedef long double ldb;
typedef pair<ll, ll> pii;

ll n, m, K, tot, a[99], tt;
pii b[99999];

struct node {
	int op, x, y;
	node(int a = 0, int b = 0, int c = 0) : op(a), x(b), y(c) {}
};
vector<node> ans;

// swap (x, y) and (x, y + 1), x < n
inline void work1(int x, int y) {
	ans.pb(1, x, y);
	ans.pb(1, x, y);
	ans.pb(2, x, y);
	ans.pb(1, x, y);
}

// swap (x, y) and (x + 1, y), y < m
inline void work2(int x, int y) {
	ans.pb(1, x, y);
	ans.pb(2, x, y);
	ans.pb(1, x, y);
	ans.pb(1, x, y);
}

// swap (x, y) and (x, y + 1), x = n
inline void work3(int x, int y) {
	ans.pb(1, x - 1, y);
	ans.pb(2, x - 1, y);
	ans.pb(2, x - 1, y);
}

// swap (x, y) and (x + 1, y), y = m
inline void work4(int x, int y) {
	ans.pb(1, x, y - 1);
	ans.pb(1, x, y - 1);
	ans.pb(1, x, y - 1);
	ans.pb(2, x, y - 1);
}

void solve() {
	scanf("%lld%lld%lld", &n, &m, &K);
	ll x = K, s = 0;
	for (ll i = 2; i * i <= x; ++i) {
		if (x % i == 0) {
			int cnt = 0;
			ll p = 1;
			while (x % i == 0) {
				x /= i;
				p *= i;
				++cnt;
			}
			s += p;
			a[++tot] = p;
		}
	}
	if (x > 1) {
		s += x;
		a[++tot] = x;
	}
	if (s > n * m) {
		puts("-1");
		return;
	}
	for (int i = 1; i <= n; ++i) {
		if (i & 1) {
			for (int j = 1; j <= m; ++j) {
				b[++tt] = mkp(i, j);
			}
		} else {
			for (int j = m; j; --j) {
				b[++tt] = mkp(i, j);
			}
		}
	}
	s = 0;
	for (int i = 1; i <= tot; ++i) {
		for (int j = s + 1; j < s + a[i]; ++j) {
			pii p = b[j], q = b[j + 1];
			if (p > q) {
				swap(p, q);
			}
			if (p.fst == q.fst) {
				if (p.fst < n) {
					work1(p.fst, p.scd);
				} else {
					work3(p.fst, p.scd);
				}
			} else {
				if (p.scd < m) {
					work2(p.fst, p.scd);
				} else {
					work4(p.fst, p.scd);
				}
			}
		}
		s += a[i];
	}
	printf("%d\n", (int)ans.size());
	for (node u : ans) {
		printf("%c %d %d\n", u.op == 1 ? 'R' : 'T', u.x, u.y);
	}
}

int main() {
	int T = 1;
	// scanf("%d", &T);
	while (T--) {
		solve();
	}
	return 0;
}