第九章课后习题

习题9.2

点击查看代码

import numpy as np
from scipy.stats import norm, chi2, chisquare
import pylab as plt

n = 50; k = 6
a = np.loadtxt('ti9.2.txt').flatten()
mu = a.mean(); s = a.std(ddof=1)
x1 = a.min(); x2 = a.max()
x = np.linspace(14.55, 15.55, k)
bin = np.hstack([x1, x, x2])
h = plt.hist(a, bin); f = h[0]
p1 = norm.cdf(x, mu, s)
p2 = np.hstack([p1[0], np.diff(p1), 1 - p1[-1]])
print('各区间的频数：', f)
print('各区间概率为：', np.round(p2,4))
ex = n * p2
kf1 = chisquare(f, ex, ddof=2)
kf2 = sum(f ** 2 / (n * p2)) - n
ka = chi2.ppf(0.95, k - 2)
print(kf1); print(round(kf2,4))
print('学号：3001')

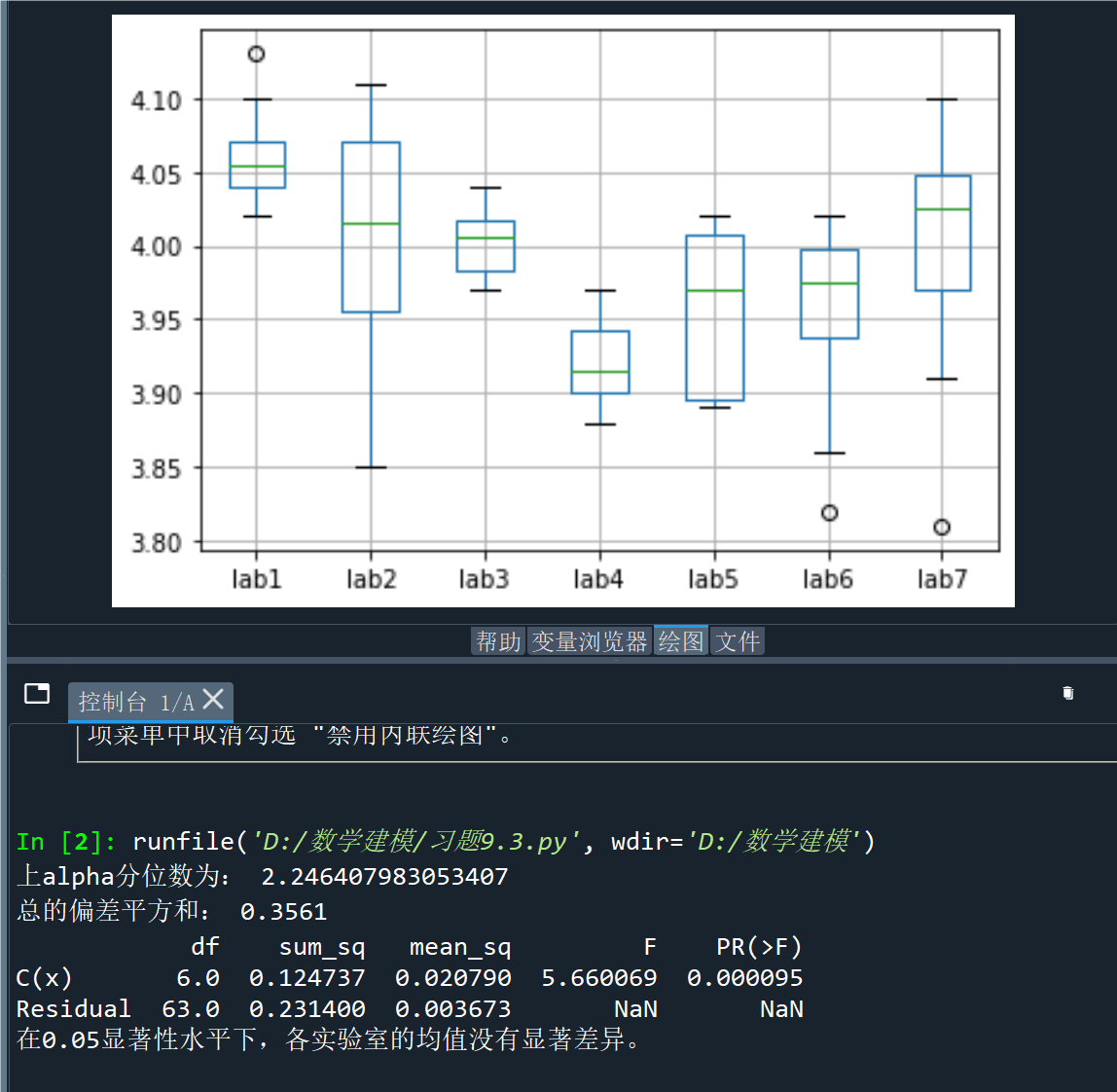
习题9.3

点击查看代码

import numpy as np
import pylab as plt
import pandas as pd
import statsmodels.api as sm
from scipy.stats import f

# 读取数据
a = pd.read_excel('data9.3.xlsx')
a.boxplot()  # 画箱线图
b = a.values.flatten()

# 计算上alpha分位数
print('上alpha分位数为：', f.ppf(0.95, 6, 63))

# 构造类别变量x
x = np.tile(np.arange(1, 8), (10, 1)).flatten()
d = {'x': x, 'y': b}  # x为类别变量

# 拟合模型并进行单因素方差分析
model = sm.formula.ols('y ~ C(x)', d).fit()
anova = sm.stats.anova_lm(model)  # 进行单因素方差分析

# 输出总的偏差平方和
print('总的偏差平方和：', round(sum(anova.sum_sq), 4))
print(anova)

# 获取p-value值
p_value = anova['PR(>F)'].iloc[-1]
alpha = 0.05  # 设定显著性水平

# 判断是否有显著差异
if p_value < alpha:
    print("在0.05显著性水平下，各实验室的均值有显著差异。")
else:
    print("在0.05显著性水平下，各实验室的均值没有显著差异。")

plt.show()
print('学号：3001')

习题9.4

点击查看代码

import numpy as np
import statsmodels.api as sm

y = np.loadtxt('ti9_4.txt',encoding='utf-8').flatten()
x1 = np.tile(np.arange(1,4), (12, 1)).T.flatten()
x2 = np.tile(np.hstack([np.ones(3), 2 * np.ones(3), 3 * np.ones(3),
4 * np.ones(3)]), (3, 1)).flatten()
d = {'x1':x1, 'x2':x2, 'y':y}
md = sm.formula.ols('y~C(x1) * C(x2)', d).fit()
ano = sm.stats.anova_lm(md)
print(ano); print('总偏差平方和:', sum(ano.sum_sq))

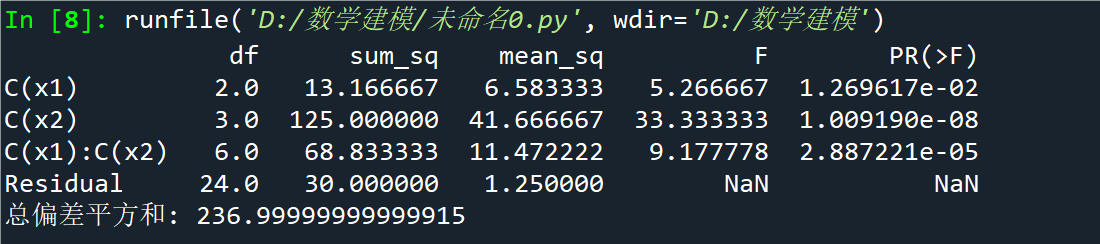
习题9.5
p值小于0.05为显著差异

点击查看代码

import numpy as np
import statsmodels.api as sm

y = np.loadtxt('ti9_5.txt').T.flatten()
x1 = np.tile(np.hstack([np.ones(4), 2 * np.ones(4), 3 * np.ones(4)]), (4, 1)).flatten()
x2 = np.tile(np.tile([1, 1, 2, 2], (1, 3)), (4, 1)).flatten()
x3 = np.tile(np.tile([1, 2], (1, 6)), (4, 1)).flatten()
d = {'x1': x1, 'x2': x2, 'x3': x3, 'y': y}
md = sm.formula.ols('y ~ C(x1) * C(x2) * C(x3)', d).fit()
ano = sm.stats.anova_lm(md)
print(ano)
print('总偏差平方和:', sum(ano.sum_sq))

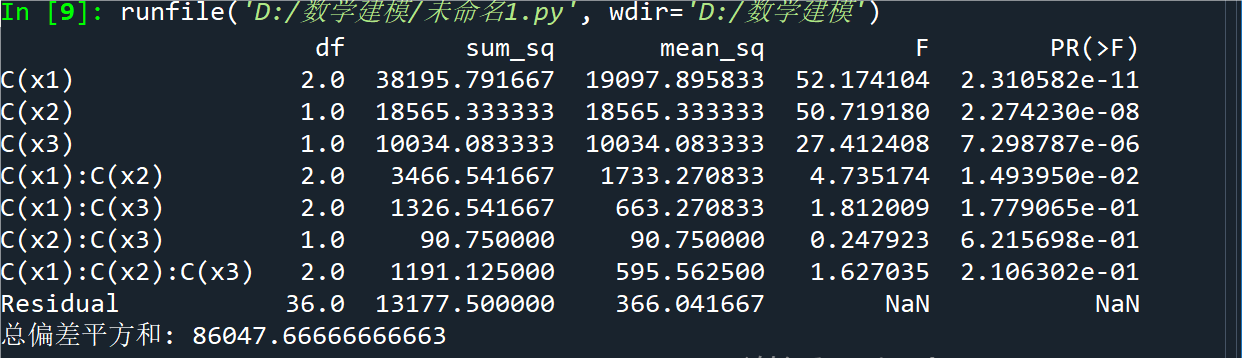
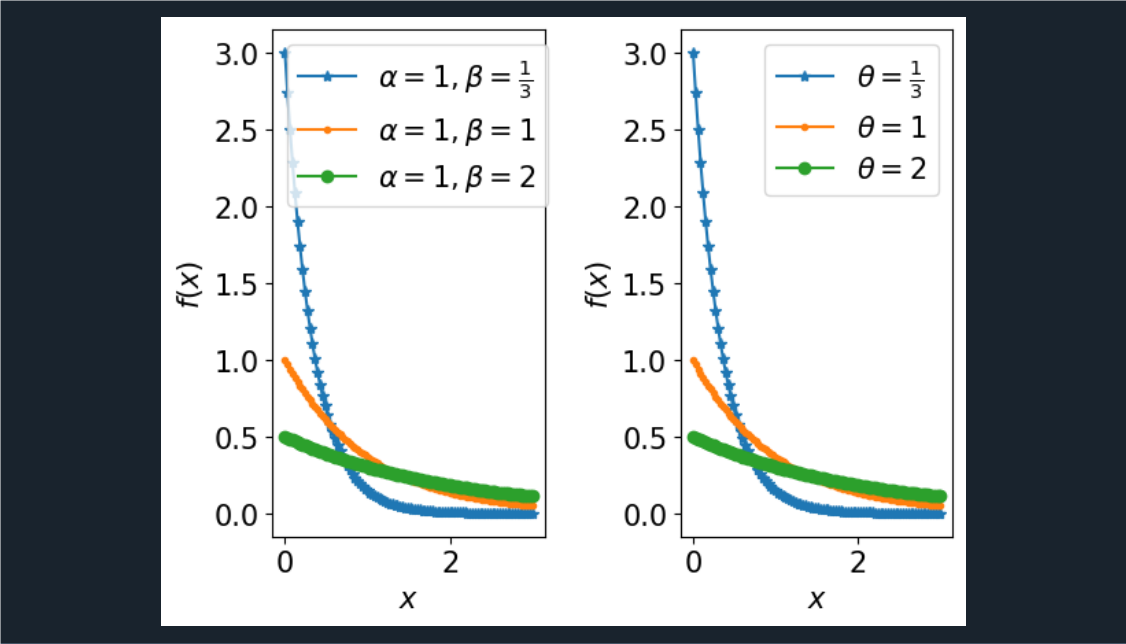
例9.1

点击查看代码

from scipy.stats import expon, gamma
import pylab as plt

x = plt.linspace(0, 3, 100)
L = [1/3, 1, 2]
s1 = ['*-', '.-', 'o-']
s2 = ['$\\alpha=1,\\beta=\\frac{1}{3}$','$\\alpha=1,\\beta=1 $', '$\\alpha=1,\\beta=2 $']
s3 = ['$\\theta=\\frac{1}{3}$','$\\theta=1 $', '$\\theta=2 $']
#plt.rc('text', usetex=False)
plt.style.use('default')
plt.rc('font', size=15)
plt.subplots_adjust(wspace=0.5)
plt.subplot(121)
for i in range(len(L)):
    plt.plot(x, gamma.pdf(x,1,scale=L[i]),s1[i], label=s2[i])
plt.xlabel('$x $')
plt.ylabel('$f(x)$')
plt.legend()
plt.subplot(122)
for i in range(len(L)):
    plt.plot(x, expon.pdf(x,scale=L[i]),s1[i], label=s3[i])
plt.xlabel('$x $')
plt.ylabel('$f(x)$')
plt.legend()
plt.show() 

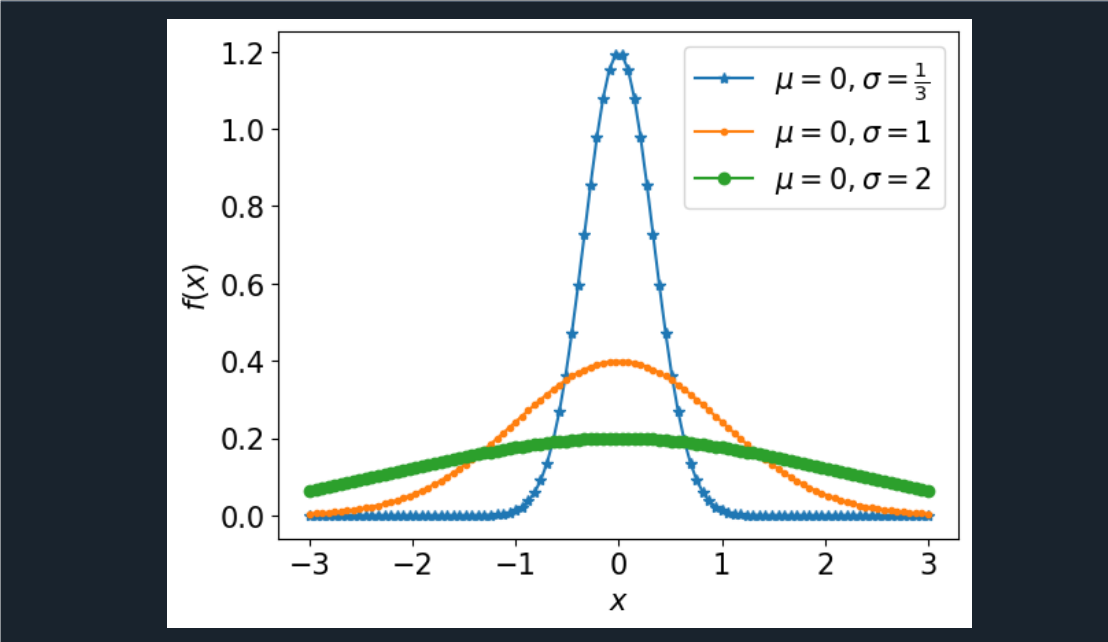
正态分布图

点击查看代码

from scipy.stats import norm
import pylab as plt

# 生成x轴的数据点
x = plt.linspace(-3, 3, 100)
# 定义不同的标准差
sigma_values = [1/3, 1, 2]
# 样式和标签
styles = ['*-', '.-', 'o-']
labels = ['$\\mu=0,\\sigma=\\frac{1}{3}$', '$\\mu=0,\\sigma=1$', '$\\mu=0,\\sigma=2$']

# 设置绘图参数
plt.rc('text', usetex=False)
plt.rc('font', size=15)
plt.subplots_adjust(wspace=0.5)

# 绘制正态分布图
plt.subplot(111)  # 使用一个子图
for i in range(len(sigma_values)):
    # 绘制正态分布曲线，均值为0，标准差为sigma_values[i]
    plt.plot(x, norm.pdf(x, loc=0, scale=sigma_values[i]), styles[i], label=labels[i])

# 设置x轴和y轴标签
plt.xlabel('$x $')
plt.ylabel('$f(x)$')
# 显示图例
plt.legend()
# 显示图形
plt.show()