第八章课后习题

习题8.4

点击查看代码

from scipy.integrate import odeint
import numpy as np
import matplotlib.pyplot as plt 

# 设置 Matplotlib 不使用 LaTeX
plt.rc('font', size=15)
plt.rc('text', usetex=False)

# 定义微分方程系统
dz = lambda z, t: [-z[0]**3 - z[1], z[0] - z[1]**3]

# 时间点
t0 = np.linspace(0, 30, 201)

# 使用 odeint 求解微分方程
s = odeint(dz, [1, 0.5], t0)

# 创建图形和子图
plt.figure(figsize=(12, 6))

# 第一个子图：时间 vs S_x 和 S_y
plt.subplot(121)
plt.plot(t0, s[:, 0], '--', label='S_x(t)')  
plt.plot(t0, s[:, 1], label='S_y(t)')        
plt.legend()
plt.xlabel('Time')  
plt.ylabel('S_x and S_y')  
plt.title('S_x(t) and S_y(t) over time')  

# 第二个子图：S_x vs S_y
plt.subplot(122)
plt.plot(s[:, 0], s[:, 1])
plt.xlabel('S_x')  
plt.ylabel('S_y')  
plt.title('S_x vs S_y') 

# 显示图形
plt.tight_layout()
plt.show()
print('学号：3001')

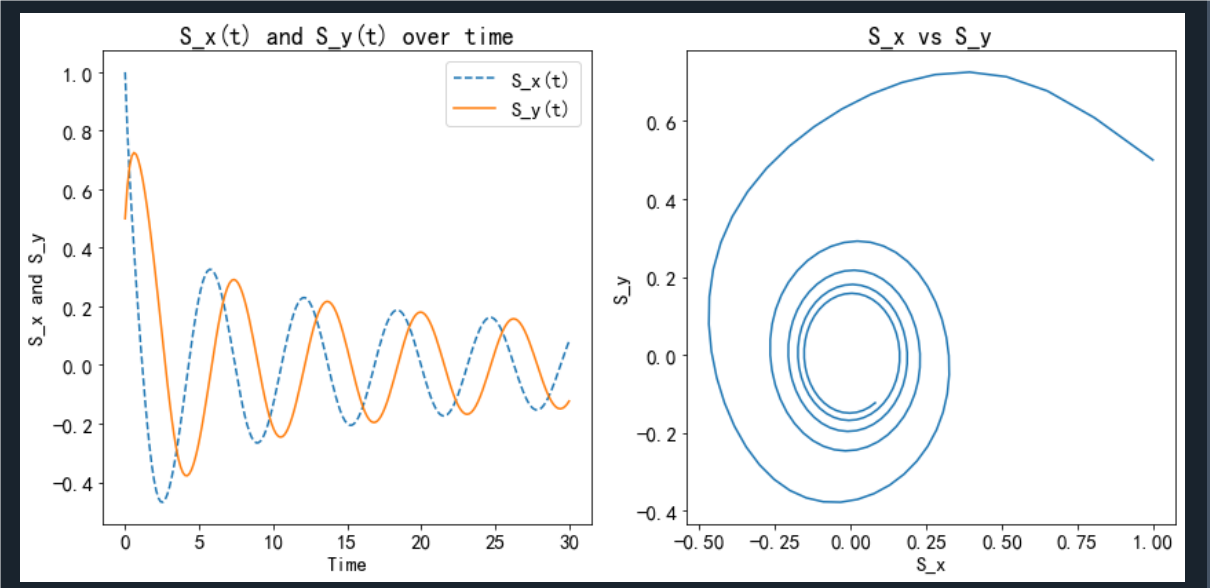
习题8.5

点击查看代码

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp

# 设置 Matplotlib 不使用 LaTeX
plt.rcParams['text.usetex'] = False

def model(t, y):
    f, df_dm, d2f_dm2, T, dT_dm = y
    d3f_dm3 = -3 * f * d2f_dm2 + 2 * (df_dm)**2 - T
    d2T_dm2 = -2.1 * f * dT_dm
    return [df_dm, d2f_dm2, d3f_dm3, dT_dm, d2T_dm2]

y0 = [0, 0, 0.68, 1, -0.5]

t_span = (0, 10)
t_eval = np.linspace(t_span[0], t_span[1], 1000)

sol = solve_ivp(model, t_span, y0, t_eval=t_eval, method='RK45')

f = sol.y[0]
T = sol.y[3]

plt.figure(figsize=(12, 6))

plt.subplot(2, 1, 1)
plt.plot(sol.t, f, label='f(m)')
plt.xlabel('m (independent variable)')  # 使用纯文本标签
plt.ylabel('f(m) (dependent variable)')
plt.title('Solution for f(m) over time')  # 使用纯文本标题
plt.grid(True)

plt.subplot(2, 1, 2)
plt.plot(sol.t, T, label='T(m)', color='orange')
plt.xlabel('m (independent variable)')
plt.ylabel('T(m) (dependent variable)')
plt.title('Solution for T(m) over time')
plt.grid(True)

plt.tight_layout()
plt.show()
print('学号：3001')

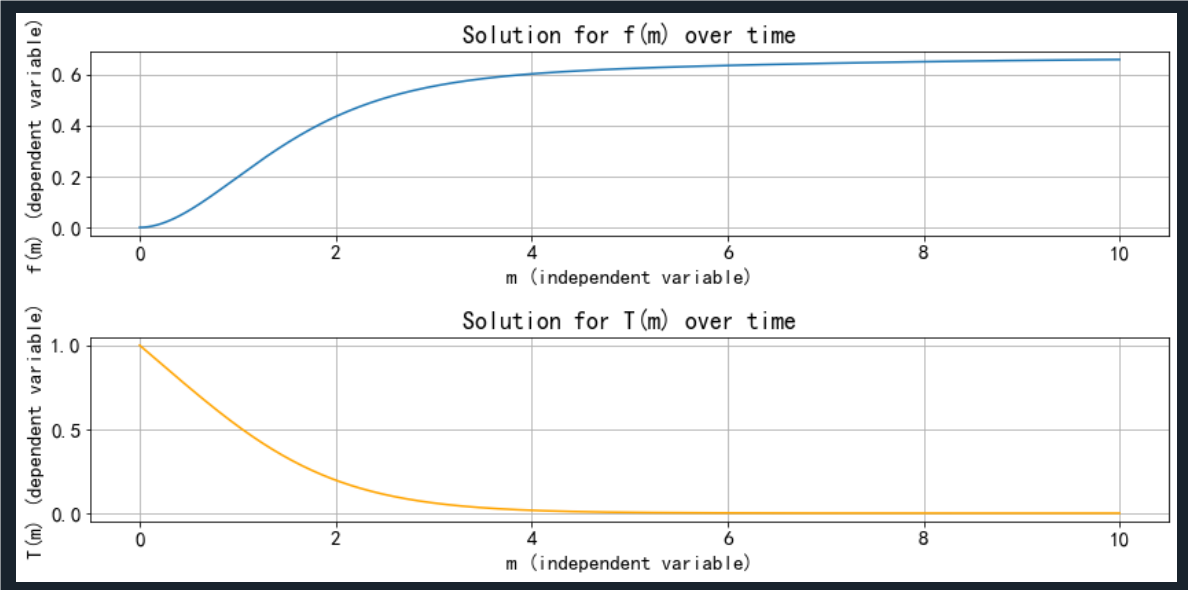
习题8.8

点击查看代码

import numpy as np
import pylab as plt
 
a = 1 - 0.2**(1/12); m = 1.109 * 10 ** 5
w3 = 17.86; w4 = 22.99
X=[]; Z=[]; N=[]
for k in np.arange(0, 0.875, 0.001):
    x1 = 1.22*10**11*(1-1/(m*(1-a-0.42*k)**8*(1-a)**24*
        (1/2+(1-a-k)**8*(1-a)**4/(1-(1-a-k)**8*(1-a)**4))))
    x2 = (1-a)**12*x1; x3 = (1-a)**12*x2;
    x4 = (1-a-0.42*k)**8*(1-a)**4/(1-(1-a-k)**8*(1-a)**4)*x3
    X.append([x1,x2,x3,x4])
    n = (m*(1-a-0.42*k)**8*(1-a)**24*(1/2+(1-a-k)**8*(1-a)**4/
        (1-(1-a-k)**8*(1-a)**4))*x1)
    N.append(n)
    z = (0.42*k*w3*(1-(1-a-0.42*k)**8)/(a+0.42*k)*x3+
         k*w4*(1-(1-a-k)**8)/(a+k)*x4)
    Z.append(z)
mz = max(np.array(Z)); ind = np.argmax(Z)
k4 = 0.001*ind; k3 = 0.42 * k4  #最优捕捞强度
print('最大生产量：', round(mz,4))
print('各年龄组鱼群数：', np.round(X[ind],4))
print('k4=',round(k4,4)); print('k3=',round(k3,4))
plt.rc('text', usetex=False); plt.rc('font', size=16)
#plt.style.use('default')
plt.plot(np.arange(0, 0.875, 0.001), Z)
plt.ylabel('$z$', rotation=0)
plt.xlabel('$k$'); plt.show()
print('学号：3001')

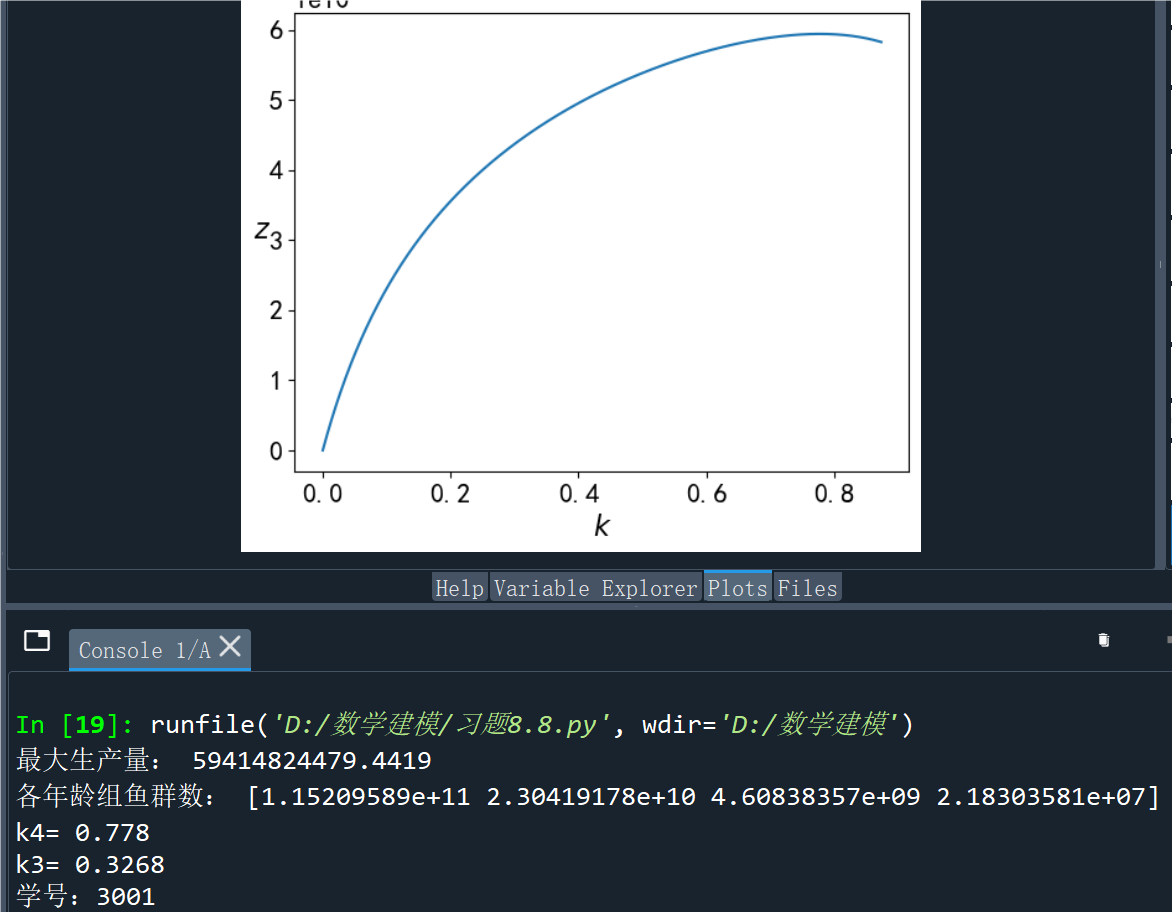
习题8.9

点击查看代码

r = 0.0036; N = 360; Q = 400000
x = round((1+r)**N*Q*r/((1+r)**N-1),2)#月还款额
xt = x*N  #总还款额
print('x=',x); print('xt=',xt)
print('学号：3001')

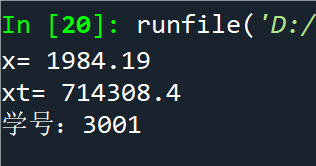
例8.3

点击查看代码

import sympy as sp
sp.var('x');y=sp.Function('y')
eq=y(x).diff(x)+2*y(x)-2*x**2-2*x
s=sp.dsolve(eq,ics={y(0):1})
s=sp.simplify(s);print(s)
import sympy as sp

例8.4

点击查看代码

import sympy as sp
sp.var('x');y=sp.Function('y')
eq=y(x).diff(x,2)-2*y(x).diff(x)+y(x)-sp.exp(x)
con={y(0):1,y(x).diff(x).subs(x,0):-1}
s=sp.dsolve(eq,ics=con);print(s)

例8.5

点击查看代码

import sympy as sp
sp.var('t');y=sp.Function('y')
u=sp.exp(-t)*sp.cos(t)
eq=y(t).diff(t,4)+10*y(t).diff(t,3)+35*y(t).diff(t,2)+\
    50*y(t).diff(t)+24*y(t)-u.diff(t,2)
con={y(0):0,y(t).diff(t).subs(t,0):-1,
     y(t).diff(t,2).subs(t,0):1,y(t).diff(t,3).subs(t,0):1}
s=sp.dsolve(eq,ics=con);s=sp.expand(s)
print(s);print('------');print(s.args[1])