线性回归算法

1.本节重点知识点用自己的话总结出来，可以配上图片，以及说明该知识点的重要性

1）。机器学习算法中回归算法的分类

2）回归与分类的区别

分类和回归的区别在于输出变量的类型（预测的目标函数是否连续）。

定量输出称为回归，或者说是连续变量预测；

定性输出称为分类，或者说是离散变量预测。

 

3）线性回归的定义

定义：线性回归通过一个或者多个自变量与因变量之间进行建模的回归方法，其中可以为一个或者多个自变量之间的线性组合。

4）线性模型：

回归分析中，只包括一个自变量个一个因变量，且二者的关系可用一条直线近似便是，这种回归分析称为医院线性回归分析。如果回归分析中包括两个或两个以上的自变量。且自变量和因变量之间是线性关系，则称为多元线性回归分析。

线性关系模型方程式

 5）线性回归的损失

　　任何一件事的过程都有一定的误差，预测也不例外，而这个范围称为最小二乘法。

6）明确线性回归算法的缺点，并对其进行优化。

7).本章主要内容总结

 

 

2.思考线性回归算法可以用来做什么？

对大量的观测数据进行处理，从而得到比较符合事物内部规律的数学表达式。也就是说寻找到数据与数据之间的规律所在，从而就可以模拟出结果，也就是对结果进行预测。解决的就是通过已知的数据得到未知的结果。例如：对房价的预测、判断信用评价、电影票房预估等。

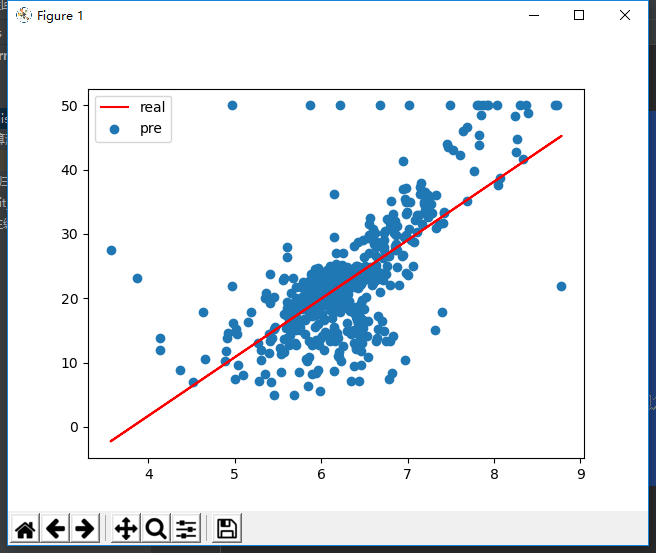
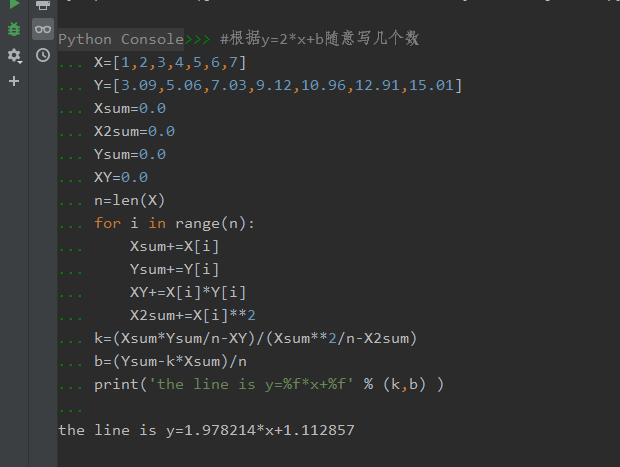
3.自主编写线性回归算法 ，数据可以自己造，或者从网上获取。（加分题）

from sklearn.linear_model import LinearRegression, SGDRegressor, Ridge
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import load_boston
from sklearn.cross_validation import train_test_split
from sklearn.metrics import mean_squared_error,classification_report
from sklearn.cluster import KMeans
 
 
def linearmodel():
    """
    线性回归对波士顿数据集处理
    :return: None
    """
 
    # 1、加载数据集
 
    ld = load_boston()
 
    x_train,x_test,y_train,y_test = train_test_split(ld.data,ld.target,test_size=0.25)
 
    # 2、标准化处理
 
    # 特征值处理
    std_x = StandardScaler()
    x_train = std_x.fit_transform(x_train)
    x_test = std_x.transform(x_test)
 
 
    # 目标值进行处理
 
    std_y  = StandardScaler()
    y_train = std_y.fit_transform(y_train)
    y_test = std_y.transform(y_test)
 
    # 3、估计器流程
 
    # LinearRegression
    lr = LinearRegression()
 
    lr.fit(x_train,y_train)
 
    # print(lr.coef_)
 
    y_lr_predict = lr.predict(x_test)
 
    y_lr_predict = std_y.inverse_transform(y_lr_predict)
 
    print("Lr预测值：",y_lr_predict)
 
 
    # SGDRegressor
    sgd = SGDRegressor()
 
    sgd.fit(x_train,y_train)
 
    # print(sgd.coef_)
 
    y_sgd_predict = sgd.predict(x_test)
 
    y_sgd_predict = std_y.inverse_transform(y_sgd_predict)
 
    print("SGD预测值：",y_sgd_predict)
 
    # 带有正则化的岭回归
 
    rd = Ridge(alpha=0.01)
 
    rd.fit(x_train,y_train)
 
    y_rd_predict = rd.predict(x_test)
 
    y_rd_predict = std_y.inverse_transform(y_rd_predict)
 
    print(rd.coef_)
 
    # 两种模型评估结果
 
    print("lr的均方误差为：",mean_squared_error(std_y.inverse_transform(y_test),y_lr_predict))
 
    print("SGD的均方误差为：",mean_squared_error(std_y.inverse_transform(y_test),y_sgd_predict))
 
    print("Ridge的均方误差为：",mean_squared_error(std_y.inverse_transform(y_test),y_rd_predict))
 
    return None