CMU 15-445 2022 Project2 B Plus Tree
前言
因为2021版没办法进行线上测试了,受不了,转战2022版。
对比2021年版的使用Extendible hashing完成索引到RID的映射,B+树则是更为经典的方法。
在之前,没具体学习过B+树的相关知识,所以这个实验做的十分波折,幸运的是最后坚持了下来。

哈哈,速度勉勉强强,和大佬没法比。没办法,前面的实验省了懒,都是一把大锁走天下。
什么是B+树?
这里引用知乎大佬的B+树基本知识总结:
B+ 树是一种树数据结构,是一个n叉树,每个节点通常有多个孩子,一颗B+树包含根节点、内部节点和叶子节点。B+ 树通常用于数据库和操作系统的文件系统中。 B+ 树的特点是能够保持数据稳定有序,其插入与修改拥有较稳定的对数时间复杂度。 B+ 树元素自底向上插入。
一个m阶的B树具有如下几个特征:
1.根结点至少有两个子女。
2.每个中间节点都至少包含ceil(m / 2)个孩子,最多有m个孩子。
3.每一个叶子节点都包含k-1个元素,其中 m/2 <= k <= m。
4.所有的叶子结点都位于同一层。
5.每个节点中的元素从小到大排列,节点当中k-1个元素正好是k个孩子包含的元素的值域分划。
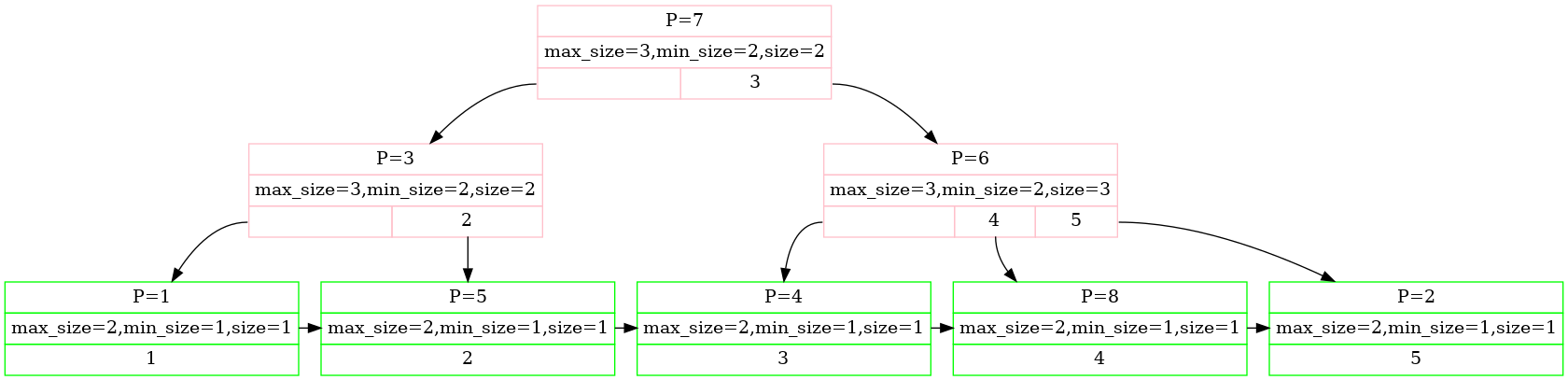
上图就是一个非常简单的B+树,它的内部节点的最大容量是3,叶子节点的最大容量是2。
最底层的叶子节点其实就是一个递增的列表,查找时,从顶层的根节点往下遍历。
叶子节点和中间节点的Key没有区别,都是hash函数得到的KeyType。但是叶子节点存储的Value是RID,中间节点的Value则是page_id(用于找到下一层的节点,因为里面的每一个节点都可以看作为一个Page)
后面开始看实验的具体任务。
CHECKPOINT #1
B+Tree Pages
需要实现三个Page类来存储B+树的数据。
- B+Tree Parent Page
- B+Tree Internal Page
- B+Tree Leaf Page
B+Tree Parent Page
这是Internal Page和Leaf Page都继承自的父类。父页面仅包含两个子类共享的信息。父页面分为几个字段,如下表所示:

它里面的实现都非常简单,唯一值得注意的是 GetMinSize 函数,因为上面说过叶子节点和中间节点的 MinSize 是有点区别的。
auto BPlusTreePage::GetMinSize() const -> int {
if (IsLeafPage()) {
return max_size_ >> 1;
}
return (max_size_ + 1) >> 1;
}
B+Tree Leaf Page
Leaf Page存储有序的m个键条目和m个值条目。在实现中,值应该仅为64位record_id,用于定位实际元组的存储位置,具体参阅 src/include/common/RID.h 中在下定义的RID类。叶页对键/值对的数量的限制与内部页相同,并且应该遵循相同的合并、重分发和拆分操作。
每个B+树叶/内部页面对应于缓冲池获取的内存页面的内容(数据部分 data_)。因此,每次尝试读取或写入叶/内部页面时,都需要首先使用其唯一的page_id从缓冲池中获取页面,然后将强制转换重新解释为叶子或内部页面,并在执行任何写入或读取操作后Unpin页面。
给我们的代码里面只有一些最基础的功能,我们需要自己多加完善,下面是我加的几个对后面操作有帮助的方法。
INDEX_TEMPLATE_ARGUMENTS
auto B_PLUS_TREE_LEAF_PAGE_TYPE::Insert(const KeyType &key, const ValueType &value, const KeyComparator &comparator)
-> int {
int idx = LowerBound(key, comparator);
if (idx == GetSize()) {
*(array_ + idx) = {key, value};
IncreaseSize(1);
return GetSize();
}
if (idx == -1) {
return GetSize();
}
std::move_backward(array_ + idx, array_ + GetSize(), array_ + GetSize() + 1);
*(array_ + idx) = {key, value};
IncreaseSize(1);
return GetSize();
}
用于插入一个KV。
INDEX_TEMPLATE_ARGUMENTS
auto B_PLUS_TREE_LEAF_PAGE_TYPE::Remove(const KeyType &key, const KeyComparator &comparator) -> int {
if (GetSize() == 0) {
return GetSize();
}
int idx = KeyIndex(key, comparator);
if (idx == -1) {
return GetSize();
}
if (idx == GetSize() - 1) {
IncreaseSize(-1);
return GetSize();
}
std::copy(array_ + idx + 1, array_ + GetSize(), array_ + idx);
IncreaseSize(-1);
return GetSize();
}
用于删除Key对应的KV
INDEX_TEMPLATE_ARGUMENTS
auto B_PLUS_TREE_LEAF_PAGE_TYPE::LowerBound(const KeyType &key, const KeyComparator &comparator) const -> int {
auto target = std::lower_bound(array_, array_ + GetSize(), key,
[&comparator](const auto &pair, auto k) { return comparator(pair.first, k) < 0; });
int idx = std::distance(array_, target);
if (idx != GetSize() && comparator(array_[idx].first, key) == 0) {
return -1;
}
return idx;
}
返回第一个比key大的槽位,相同返回-1
INDEX_TEMPLATE_ARGUMENTS
auto B_PLUS_TREE_LEAF_PAGE_TYPE::KeyIndex(const KeyType &key, const KeyComparator &comparator) const -> int {
auto target = std::lower_bound(array_, array_ + GetSize(), key,
[&comparator](const auto &pair, auto k) { return comparator(pair.first, k) < 0; });
int dis = std::distance(array_, target);
if (dis == GetSize() || comparator(array_[dis].first, key) != 0) {
return -1;
}
return dis;
}
返回key所在槽位,无则返回-1
还有一些其他的工具方法,就不一一展示了,每个人的实现不同,所以会有不同的工具方法。
B+Tree Internal Page
内部页面不存储任何实际数据,而是存储有序的m个密钥条目和m+1个子指针(也称为Page_id)。由于指针的数量不等于键的数量,因此第一个键被设置为无效,查找方法应始终从第二个键开始。在任何时候,每个内部页面都至少有一半是满的。在删除过程中,可以将两个半完整的页面合并为合法页面,也可以重新分发以避免合并,而在插入过程中,一个完整的页面可以一分为二。这是在实现B+树时将要进行的众多设计选择之一的示例。
因为有这些不同,虽然需要实现的方法和叶子节点大差不差,但细节很多需要注意。如:
INDEX_TEMPLATE_ARGUMENTS
auto B_PLUS_TREE_INTERNAL_PAGE_TYPE::KeyIndex(const KeyType &key, const KeyComparator &comparator) const -> int {
auto target = std::lower_bound(array_ + 1, array_ + GetSize(), key,
[&comparator](const auto &pair, auto k) { return comparator(pair.first, k) < 0; });
int dis = std::distance(array_, target);
if (dis == GetSize() || comparator(array_[dis].first, key) != 0) {
dis--;
}
return dis;
}
第一个Key没有意义,所以我们要从下标1开始找。
INDEX_TEMPLATE_ARGUMENTS
auto B_PLUS_TREE_INTERNAL_PAGE_TYPE::LowerBound(const KeyType &key, const KeyComparator &comparator) const -> int {
auto target = std::lower_bound(array_ + 1, array_ + GetSize(), key,
[&comparator](const auto &pair, auto k) { return comparator(pair.first, k) < 0; });
int dis = std::distance(array_, target);
if (dis != GetSize() && comparator(array_[dis].first, key) == 0) {
return -1;
}
return dis;
}
找第一个大于Key的槽也是一样。
B+Tree Data Structure
B+树索引应该只支持唯一的键。也就是说,当您试图将具有重复键的键值对插入到索引中时,它不应该执行插入并返回false。如果删除导致某些页面低于占用阈值,您的B+树索引也必须正确执行合并或重新分发(在教科书中称为“合并”)。
对于检查点#1,仅需要B+树索引来支持插入(insert()),点搜索(getValue())和删除(delete(delete())。如果插入触发分裂条件(插入后的键/值对数量等于叶子节点的max_size,插入之前的儿童数量等于内部节点的max_size)。
CHECKPOINT #2
Index Iterator
除了上面提到的我们需要实现 Index Iterator 用于从小到大遍历所有的叶子节点里面的KV。
构建一个通用的索引迭代器来高效地检索所有的叶页。基本思想是将它们组织成一个单独的链表,然后在特定方向上遍历存储在B+树叶页中的每个键/值对。索引迭代器应该遵循C++17中定义的迭代器的功能,包括使用一组运算符迭代一系列元素的能力,以及每个循环(至少使用增量、解引用、相等和不相等运算符)的能力。
这一部分的实现较为简单,只要确保 == 的重载能正常运行就好(用于迭代的时候与end比较然后终止)。还有就是 ++ 运算符,当此时KV是页尾的时候,需要将自身指向下一页的开头。
同时,我们也要考虑多线程的情况。这里使用的是页级锁,它已经在 Page 中实现好了,可以直接调用。
GetValue
这个函数是 BPlusTree 中用于查询给出了 public 方法。
为了避免公开代码,这里(包括后面所有的代码)省略很多的实现细节(函数参数,锁和解锁):
INDEX_TEMPLATE_ARGUMENTS
auto BPLUSTREE_TYPE::GetValue(const KeyType &key, std::vector<ValueType> *result, Transaction *transaction) -> bool {
if (IsEmpty()) {
return false;
}
Page *page = FindLeaf(key, Operation::Find);
if (page != nullptr) {
LeafPage *node_leaf = Cast2LeafPage(page);
int idx = node_leaf->KeyIndex(key, comparator_);
if (comparator_(key, node_leaf->KeyAt(idx)) == 0) {
result->push_back(node_leaf->ValueAt(idx));
}
buffer_pool_manager_->UnpinPage(page->GetPageId(), false);
}
return !result->empty();
}
里面的核心是 FindLeaf,用于锁定Key值所在的叶子节点。
INDEX_TEMPLATE_ARGUMENTS
auto BPLUSTREE_TYPE::FindLeaf(const KeyType &key, const Operation &ope) -> Page * {
Page *page = buffer_pool_manager_->FetchPage(root_page_id_);
BPlusTreePage *node = Cast2BPlusTreePage(page);
if (ope == Operation::Find) {
while (!node->IsLeafPage()) {
InternalPage *node_inter = Cast2InternalPage(node);
int idx = node_inter->KeyIndex(key, comparator_);
Page *next_page = buffer_pool_manager_->FetchPage(node_inter->ValueAt(idx));
BPlusTreePage *next_node = Cast2BPlusTreePage(next_page);
buffer_pool_manager_->UnpinPage(page->GetPageId(), false);
page = next_page;
node = next_node;
}
return page;
}
}
正如开头所介绍的那样,我们可以自上而下迅速地找到目标节点。
虽然都是查找,但是由于并发锁的设计,查找、插入和移除所对应的 FindLeaf 里面的逻辑也是不同的。
Insert
插入有两种情况:
- 插入KV后不会引发分裂(安全)
- 插入KV后会引发分裂(不安全)
首先我们先对叶子节点直接插入:
INDEX_TEMPLATE_ARGUMENTS
auto BPLUSTREE_TYPE::InsertLeaf(const KeyType &key, const ValueType &value, Transaction *transaction) -> bool {
// 插入时可能为空
if (root_page_id_ == INVALID_PAGE_ID) {
Page *root = buffer_pool_manager_->NewPage(&root_page_id_);
if (root == nullptr) {
throw Exception(ExceptionType::OUT_OF_MEMORY, "Cannot allocate new page");
}
auto *root_as_leaf = reinterpret_cast<LeafPage *>(root->GetData());
root_as_leaf->Init(root_page_id_, INVALID_PAGE_ID, leaf_max_size_);
root_as_leaf->Insert(key, value, comparator_);
left_page_ = root_page_id_;
buffer_pool_manager_->UnpinPage(root_page_id_, true);
UpdateRootPageId(1);
return true;
}
Page *page = FindLeaf(key, Operation::Insert);
LeafPage *page_as_leaf = Cast2LeafPage(page);
int old_size = page_as_leaf->GetSize();
if (IsSafe(page_as_leaf, Operation::Insert)) {
int new_size = page_as_leaf->Insert(key, value, comparator_);
buffer_pool_manager_->UnpinPage(page->GetPageId(), true);
// 插入失败说明有重复值
return new_size > old_size;
}
int new_size = page_as_leaf->Insert(key, value, comparator_);
if (new_size == old_size) {
buffer_pool_manager_->UnpinPage(page->GetPageId(), true);
return false;
}
// 插入后达到了MaxSize
// 新建一个节点,分MaxSize - MinSize的数据到里面
// 如果当前叶子节点是根节点,则直接新建一个根节点,然新旧节点指向新的根节点
// 否则转到 InsertInter 里面
return true;
}
当产生分裂节点,就需要将这个节点的KV存到父节点中去。如果父节点在存入前已经达到了MaxSize,则应该先分裂在存放。依此迭代。
INDEX_TEMPLATE_ARGUMENTS
auto BPLUSTREE_TYPE::InsertInter(page_id_t page_parent_id, const KeyType &key, page_id_t page_id, Transaction *transaction) -> void {
Page *page = buffer_pool_manager_->FetchPage(page_parent_id);
InternalPage *page_as_inter = Cast2InternalPage(page);
// 安全直接插入,返回
if (IsSafe(page_as_inter, Operation::Insert)) {
page_as_inter->Insert(key, page_id, comparator_);
buffer_pool_manager_->UnpinPage(page_parent_id, true);
return;
}
// 新建分裂的节点
page_id_t page_id_new = INVALID_PAGE_ID;
Page *page_new = buffer_pool_manager_->NewPage(&page_id_new);
InternalPage *page_as_inter_new = Cast2InternalPage(page_new);
for (int i = 0; i < page_as_inter_new->GetSize(); i++) {
// 将分出去的KV对应的子节点重新设置父节点为分裂节点
}
if (page_as_inter->IsRootPage()) {
// 当前如果是根节点,则旧节点和分裂节点需要将父节点设置为新建的根节点
} else {
// 不是根节点那只需要更改新节点的父节点,将分裂节点的KV放入当前节点的父节点
InsertInter(page_parent_id, key0, page_id_new);
}
}
Remove
和Insert逻辑是类似的先直接在叶子节点移除,如果安全直接返回,不安全再向上迭代删除,直至安全为止。
INDEX_TEMPLATE_ARGUMENTS
void BPLUSTREE_TYPE::RemoveLeaf(const KeyType &key, Transaction *transaction) {
if (IsEmpty()) {
return;
}
Page *page = FindLeaf(key, Operation::Remove);
BPlusTreePage *node = Cast2BPlusTreePage(page);
LeafPage *node_leaf = Cast2LeafPage(node);
if (IsSafe(node_leaf, Operation::Remove)) {
node_leaf->Remove(key, comparator_);
return;
}
node_leaf->Remove(key, comparator_);
// 不安全向上迭代删除
RemoveParent(page, root_locked, transaction);
}
INDEX_TEMPLATE_ARGUMENTS
auto BPLUSTREE_TYPE::RemoveParent(Page *page) -> bool {
BPlusTreePage *node = Cast2BPlusTreePage(page);
if (node->IsRootPage()) {
if (node->IsLeafPage()) {
// 如果是根节点,且此时大小为0,则将整个B+树设空
if (node->GetSize() == 0) {
root_page_id_ = INVALID_PAGE_ID;
UpdateRootPageId();
}
} else {
// 还有一个特殊情况,根节点大小为1,此时需要将其唯一的子节点设为根节点
InternalPage *old_root = Cast2InternalPage(node);
if (old_root->GetSize() == 1) {
...
}
}
return need_flush;
}
// 安全状态旧直接返回
if (node->GetSize() >= node->GetMinSize()) {
return true;
}
// 不安全:size < minsize
// 获取父节点
Page *parent_page = buffer_pool_manager_->FetchPage(node->GetParentPageId());
InternalPage *parent_node = Cast2InternalPage(parent_page);
assert(parent_node->GetSize() >= 2);
int idx = parent_node->FindIndex(page->GetPageId());
if (idx == 0) {
// idx == 0 必有右兄弟节点
BPlusTreePage *right_node = Cast2BPlusTreePage(right_page);
if (right_node->GetSize() > right_node->GetMinSize()) {
// 向右借
BorrowFromRight(node, right_node, idx + 1);
} else {
// 把右边合并,删除右节点
Merge(node, right_node, idx);
}
} else {
BPlusTreePage *left_node = Cast2BPlusTreePage(left_page);
if (left_node->GetSize() > left_node->GetMinSize()) {
// 向左借
BorrowFromLeft(node, left_node, idx - 1, transaction);
} else {
// 将自身合并到左节点,删除自己
Merge(left_node, node, idx - 1, root_locked,
}
}
注意,只有合并才会引起节点删除,也意味着在合并完后需要迭代进入 RemoveParent,继续进行父节点的调整。
并发
并发是难度最大的点。
任务要求以 latch crabbing 方案设计闩锁。闩保护的是数据结构,隔离的是线程;锁保护的是内容,隔离的是事务。
如果其子页面被视为“安全”,线程在父页面上释放 latch 。请注意,“安全”的定义可能会根据线程执行的哪种操作而有所不同。
可是怎样实现节点的删除,才能不让删除与加锁解锁相冲突。
latch crabbing
Latch Crabing 的基本思想:线程在遍历时,先获取 parent 的 latch,再获取 child 的 latch,若 child "safe",则释放 parent 的 latch。
在查找时,很容易设计:对当前页面设置读锁;获取子节点;对子节点加锁,当前节点解锁;将子节点设为当前节点。一直往下,直到当前节点是叶子节点,读取数据后,释放读锁。
插入和移除则可能会在操作的时候锁住很多节点,此时我们需要一个队列来存放锁住的节点(页面),然后在安全或者完成操作时依次释放。(使用队列的原因是便于更早地释放高层节点,降低线程冲突)
大致思路是:从根节点开始,使用写锁锁住当前节点,获取子节点;写锁锁住子节点,将当前节点放入队列;判断子节点是否安全,安全则释放队列被锁住的节点,否则不对队列中的节点进行操作。
对于插入和删除有不同的安全标准,插入中,叶子节点和中间节点也有不同的安全标准。
其他注意:删除时,借和合并需要对邻居节点进行上锁,防止其他线程或操作对邻居节点造成影响,操作完成后即可释放;删除时,向上迭代的过程中如果遇到对父节点大小没有影响的操作(对左右节点的借操作),则可以将父节点的祖宗节点提前全部释放(队列中)。
根节点保护
所有的操作都需要从根节点开始向下寻找,为了防止使用同时根节点造成冲突,实验建议单独设置一个 std::mutex 来保护根节点。每个操作开始的时候就需要获取这个锁,后续在释放根节点的锁(读锁或解锁)前都不能对其解锁。
持有锁节点的队列
实验中每个函数都有一个事务相关的参数:Transaction *transaction。如果进入这个类的定义可以发现里面就有内置的队列,我们只需要调用 GetPageSet() 和 AddIntoPageSet() 就可以实现锁住页面(节点)存取。
删除的时机
如果细心一点就会发现,在一次删除操作中,可能有很多被删除的节点,其中一些对应就是被锁住的节点,因为锁的缘故,我们只能在最后全部将锁释放了才能安全地删除他们。所以在操作过程需要有数据结构记录这些需要删除的节点。幸运的是 Transaction *transaction 里面也有这样的内置容器:unordered_set。具体操作起来非常简单。
并发测试

实验给出的较优拥塞比是[2.5, 3.5],不知道是不是有细节没控制好,测试一拥塞率有点高,测试二还可以(测试二的叶子节点最大容量设置的更高)。
其他需要注意的点就自己思考去吧,比如乐观锁的的设计、UnLock和UnPin的先后、Index Iterator的优化、降低缓冲池的访问技巧等等。
继续加油,骚年。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号